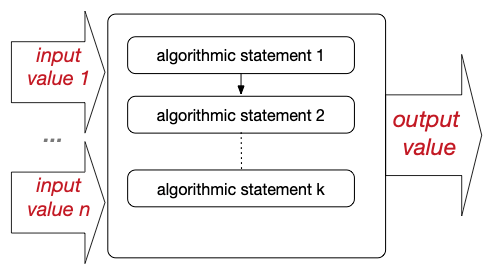
• Un algorithme est une solution à un problème spécifique qui prend un ensemble de valeurs en entrée et produit une valeur en résultat

• Cette solution est réalisée par une séquence d’instructions algorithmiques appliquées aux données d’entrée pour produire la valeur finale du résultat

Valeurs

• 34, 1.09, “IMT Atlantique” ou false sont des valeurs qui peuvent être intégrées dans des calculs

• Par exemple, 34 * 1.09 pour obtenir la conversion en euros de 34 dollars avec un taux de 1.09

Variables

• Les variables sont des noms qui réfèrent à des valeurs, tandis que les constantes sont fixes

• Favorisez toujours les variables plutôt que la réutilisation de la même valeur

• Les valeurs ont un type associé, qui définit les opérations possibles sur elles

• Les langages de programmation définissent plusieurs types élémentaires (booléens, entiers, nombres réels, chaînes de caractères, etc.) et permettent de créer vos propres types composites

• Les structures de données permettent de regrouper des types simples en collections

Éléments essentiels

• Définir des variables / assigner des valeurs (ex., a = 34 * nb)
• Opérateurs sur les variables
• Conditions
• Boucles

Un peu de sucre syntaxique

• Définir / appeler des fonctions (session de programmation 2)
• Programmation orientée objet (session de programmation 4)

Conditions

Les instructions conditionnelles (if) sont utilisées pour diviser l’exécution séquentielle de l’algorithme selon une condition booléenne :

if estimated_value - real_value < epsilon: 
    print("Estimation found:", estimated_value)
else:
    print("Continuation")

Quelques syntaxes alternatives (voir la doc match) :

if est - real < eps: 
    print("Estimation found:", est)
elif est - real < 2 * eps: 
    print("Less precise:", est)
else:
    print("Continuation")

match est - real:
    case 0 | 2 | 4: print("Even difference")
    case 6 | 8:     print("Higher even difference")
    case 3:         print("Difference of 3")
    case float():   print("Real difference")
    case  _ :       print("Something else")

Boucles

Les boucles permettent de définir des cycles dans le flux d’exécution d’un algorithme

# Initialize a few variables
v = [1, 5, -5, 15, 0]
max_v = v[O] if len(v) > 0 else None

# A bounded loop
# Wll iterate len(v) times
for i in range(len(v)):
    if v[i] > max_v:
        max_v = v[i] 

# Initialize a few variables
v = [1, 5, -5, 15, 0]
max_v = v[O] if len(v) > 0 else None
i = 0

# An unbounded loop
# Will iterate until condition is false
while i < len(v):
    if v[i] > max_v:
        max_v = v[i] 
    i += 1

Un invariant est utilisé pour prouver par induction qu’une boucle atteint effectivement un état attendu à partir d’un état initial

# This test should be true at any iteration of the loop
max_v == max(v[:i])

Un algorithme est une solution à un problème spécifique qui prend un ensemble de valeurs en entrée et produit une valeur en résultat

• Les algorithmes sont des séries d’opérations sur des variables, des conditions et des boucles

• Les boucles non bornées peuvent conduire à une exécution infinie, donc vérifiez bien votre condition

• Favorisez toujours les variables plutôt que la réutilisation de la même valeur

• Soyez conscient des types et de la mutabilité des variables