Catch a single piece of cheese
Project – Session 2
- Aborder un problème computationnel
- Graphes & chemins
- Représentation des graphes
- Parcours de graphes
- Tables de routage
- Structures de file pour les parcours de graphes
- Récapitulatif de la session
Aborder un problème computationnel
Formaliser

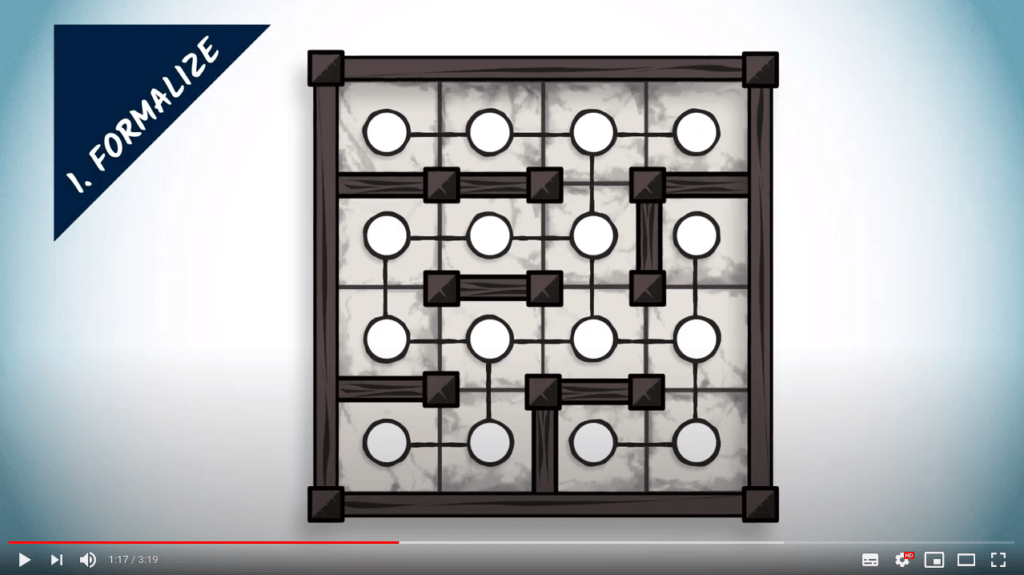
- Enlever les détails du problème qui ne sont pas nécessaires à sa résolution
- Trouver une représentation adaptée pour les éléments restants
Aborder un problème computationnel
Spécifier
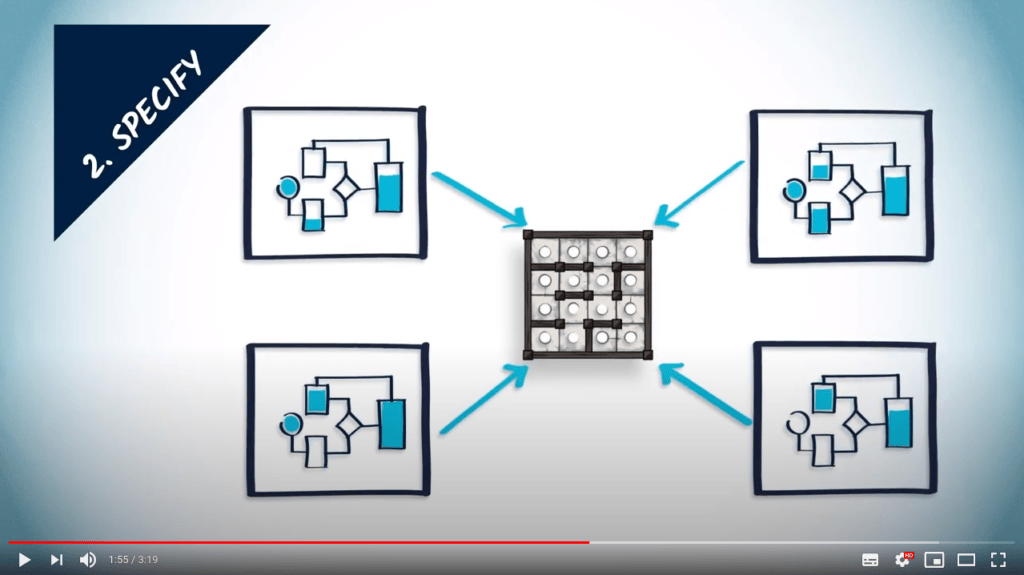
- Trouver un algorithme pour résoudre le problème, donné le formalisme choisi
- Les formalismes standards disposent de nombreux algorithmes
- Explorer les algorithmes existants avant de réinventer la roue !
Aborder un problème computationnel
Code
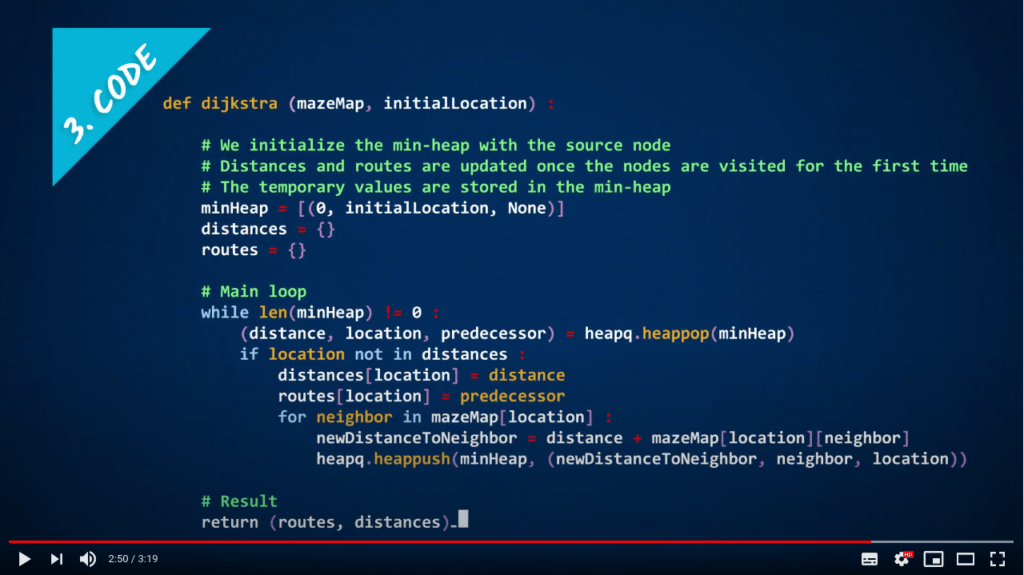
- Maintenant que vous avez un algorithme, il est temps de l’implémenter
- Encore une fois, avant de réinventer la roue, vérifiez les bibliothèques existantes !
Graphes & chemins
Qu’est-ce qu’un graphe ?

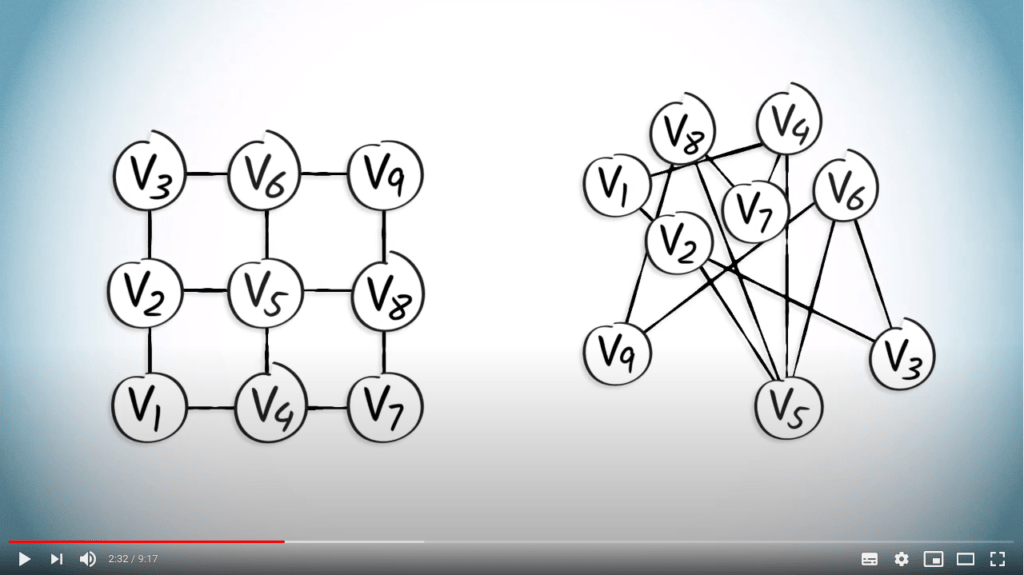
Qu’est-ce que c’est ?
- Une abstraction mathématique d’éléments d’intérêt et des liens entre eux
- Exemple, Internet, connexions dans le cerveau, relations entre variables, labyrinthe…
Formellement
- Sommets $\mathcal{V}$ et arêtes $\mathcal{E}$
- Les arêtes peuvent avoir un poids et une direction
- La représentation graphique n’est pas importante, seules les arêtes comptent
Graphes & chemins
Chemins dans les graphes
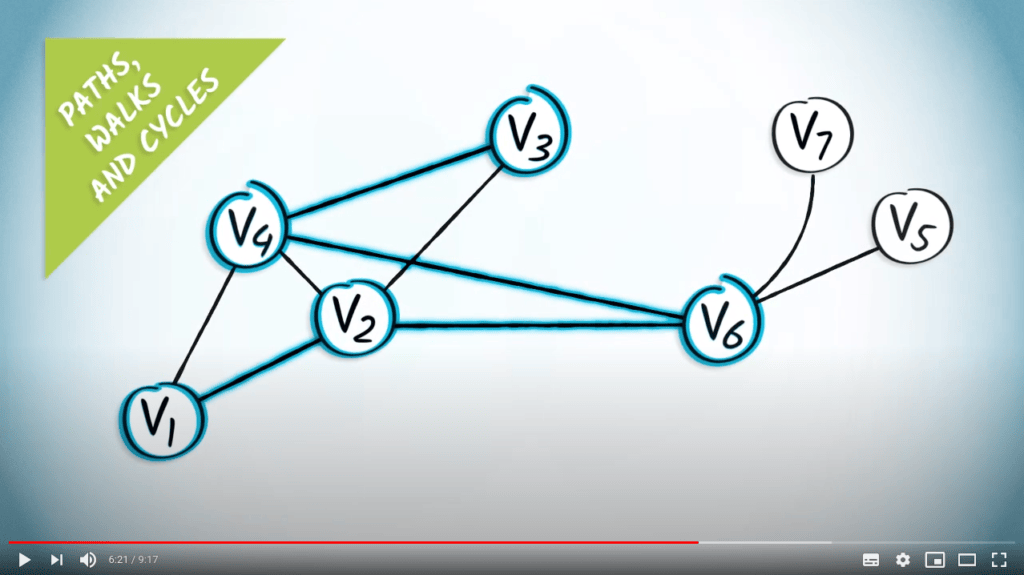
- Un chemin est une série d’arêtes sans répétition de sommet
- Les chemins ne contiennent pas de cycles
- La longueur d’un chemin est la somme de ses poids (ou le nombre d’arêtes si non pondéré)
Représentation des graphes
La matrice d’adjacence
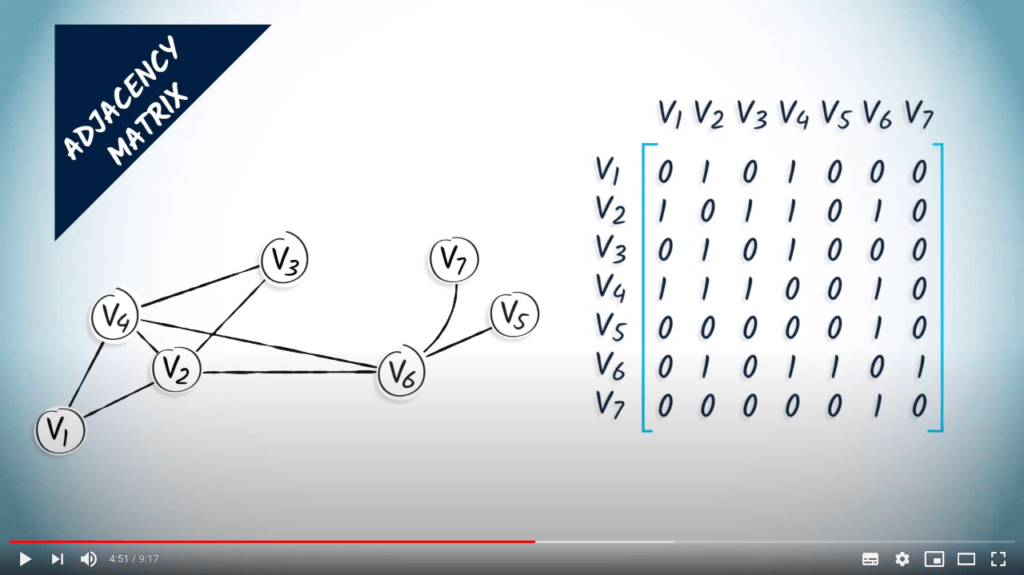
- Comment stocker une matrice d’adjacence en mémoire ? $\rightarrow$ tableau, liste de listes, dictionnaire, objet…
- Dans le logiciel PyRat, un objet fournit des moyens pour encoder et manipuler le graphe
Représentation des graphes
Détails sur la représentation PyRat
Let g be an instance of Graph:
g.vertices # Gives you a list of vertices in the graph
g.nb_vertices # Gives you the number of vertices in the graph
g.edges # Gives you the list of edges in the graph
g.nb_edges # Gives you the number of edges in the graph
g.add_vertex(v) # Adds vertex v to the graph
g.add_edge(v1, v2, w) # Adds an edge of weight w between v1 and v2
g.get_neighbors(v) # Gives you the neighbors of v in the graph
g.get_weight(v1, v2) # Gives you the weight of edge between v1 and v2
g.remove_vertex(v) # Removes vertex v and all edges attached to it from the graph
g.remove_edge(v1, v2) # Removes edge between v1 and v2 from the graph
g.is_connected() # Indicates if the graph is connected
g.has_edge(v1, v2) # Indicates if an edge exists between vertices v1 and v2
g.edge_is_symmetric(v1, v2) # Indicates if edge from v1 to v2 can be used to go from v2 to v1
g.minimum_spanning_tree() # Gives you a minimum spanning tree for the graph
g.as_dict() # Gives you a dictionary representation of the graph
g.as_numpy_ndarray() # Gives you a matrix representation of the graph (as a numpy.ndarray)
g.as_torch_tensor() # Gives you a matrix representation of the graph (as a torch.tensor)Dans PyRat, vous manipulez une instance de Maze, qui hérite de Graph $\rightarrow$ Plus d’infos dans la classe Maze !
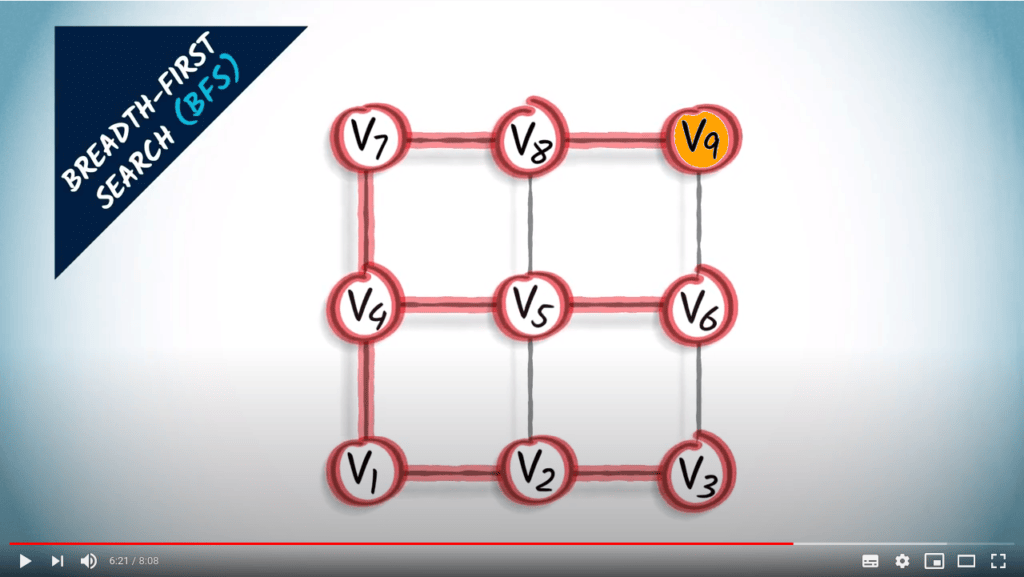
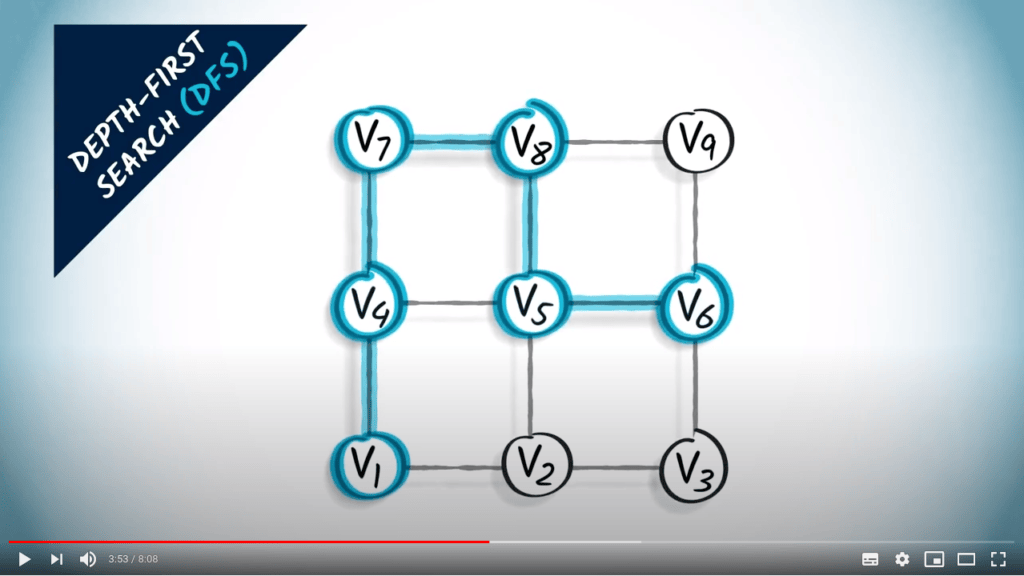
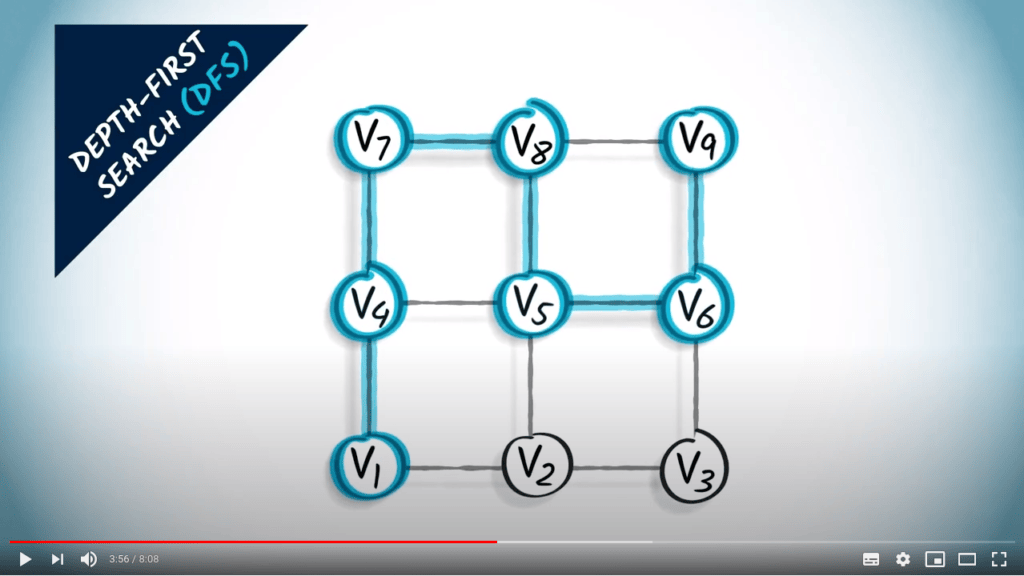
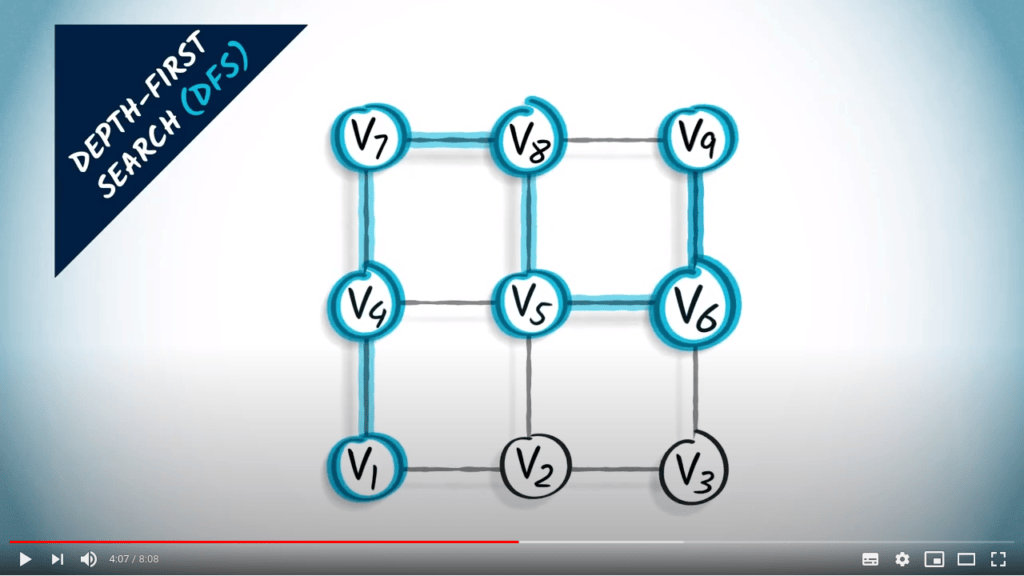
Parcours de graphes
Qu’est-ce qu’un parcours ?
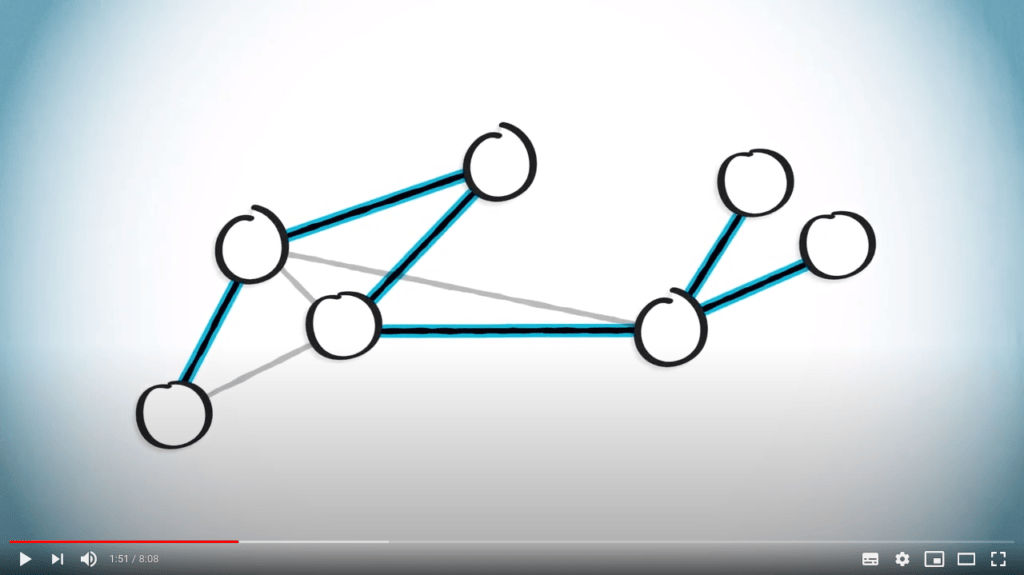
- Une manière d’explorer tous les sommets d’un graphe
- Commencer à partir d’un sommet, et aller itérativement vers ses voisins
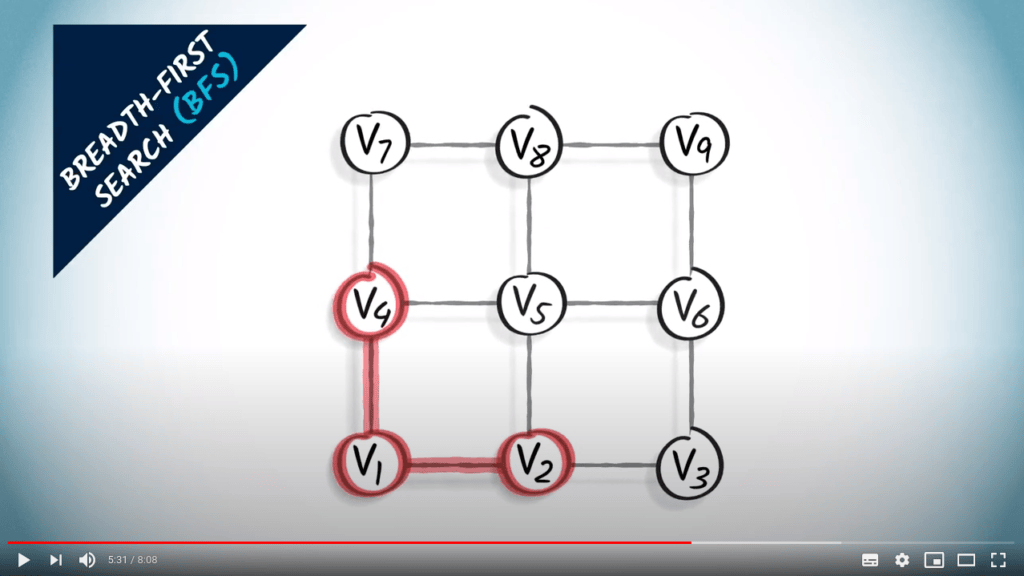
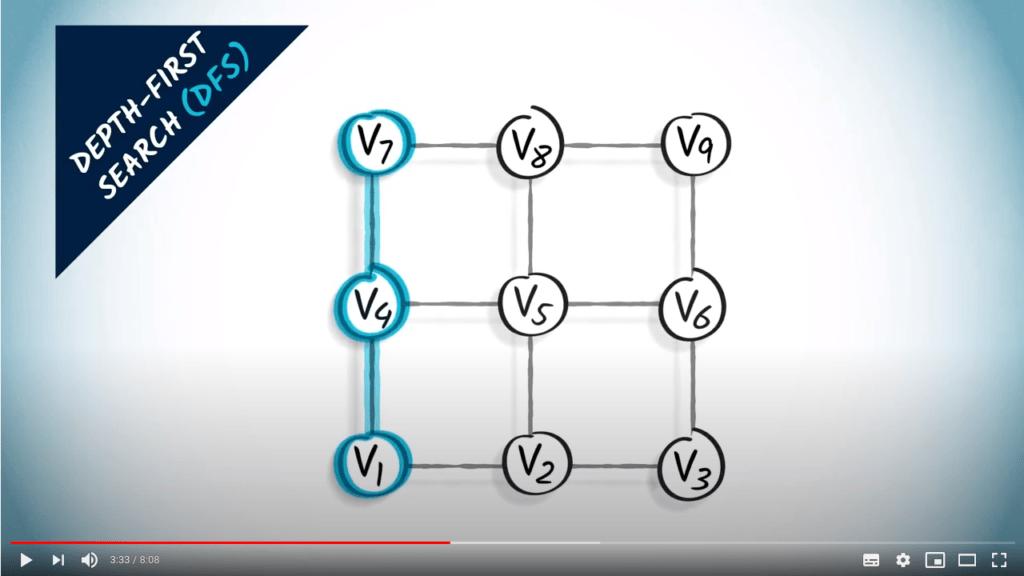
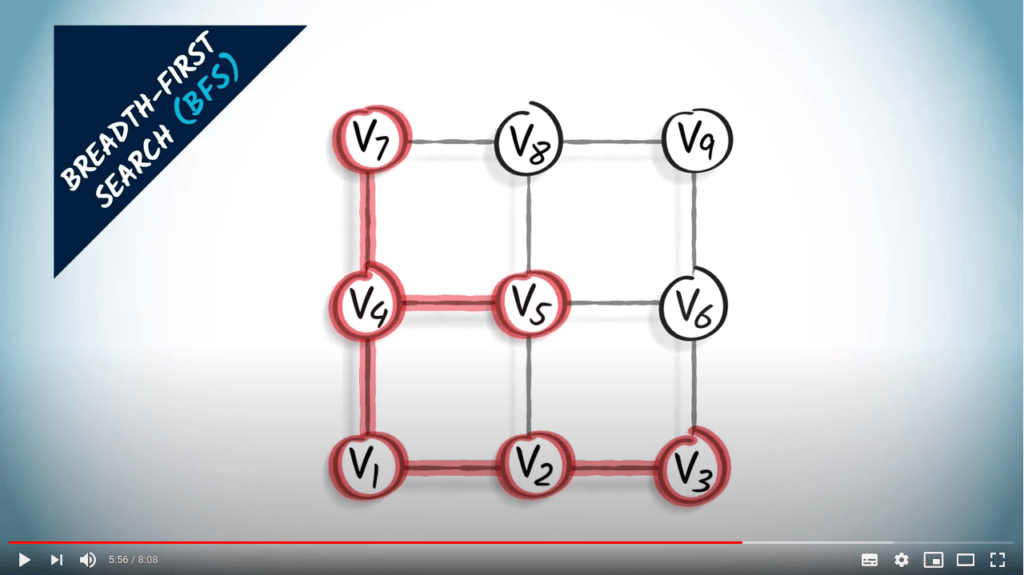
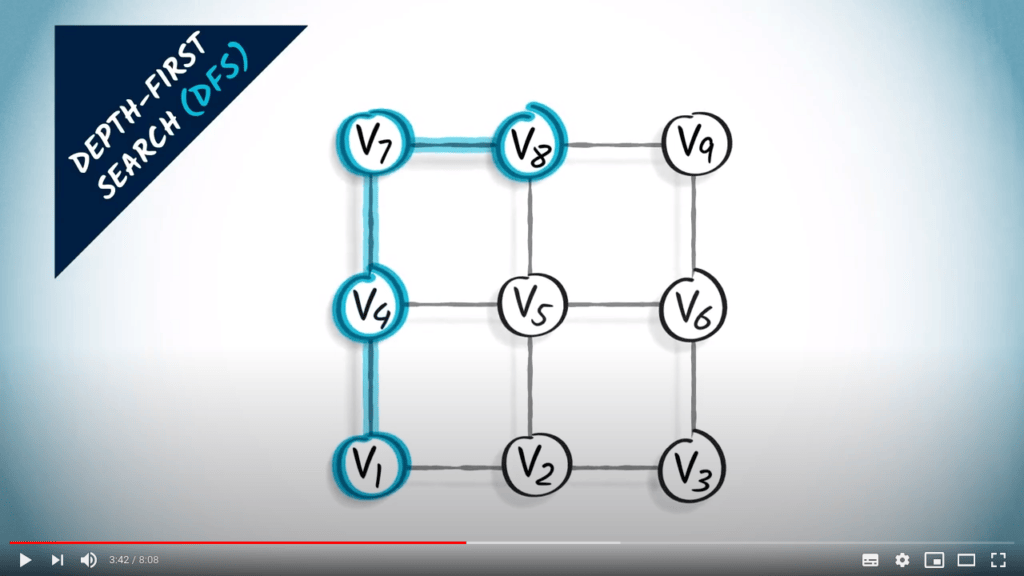
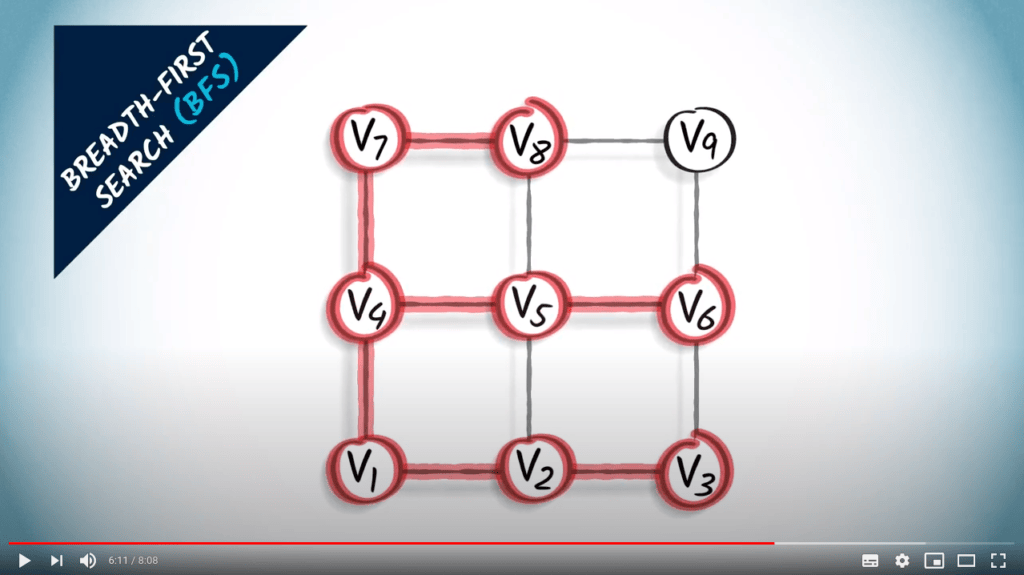
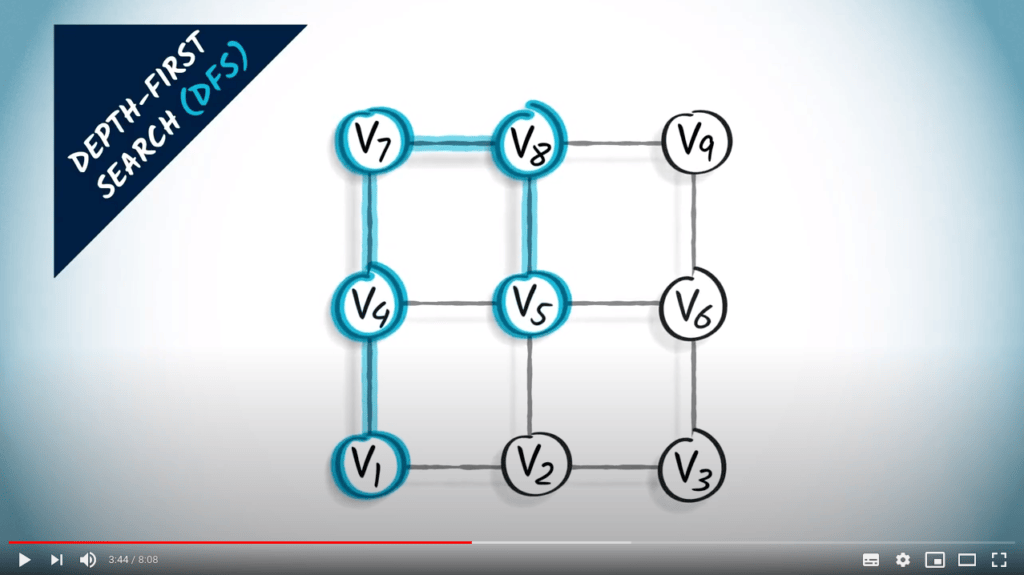
Parcours de graphes
Deux stratégies sur un graphe non pondéré
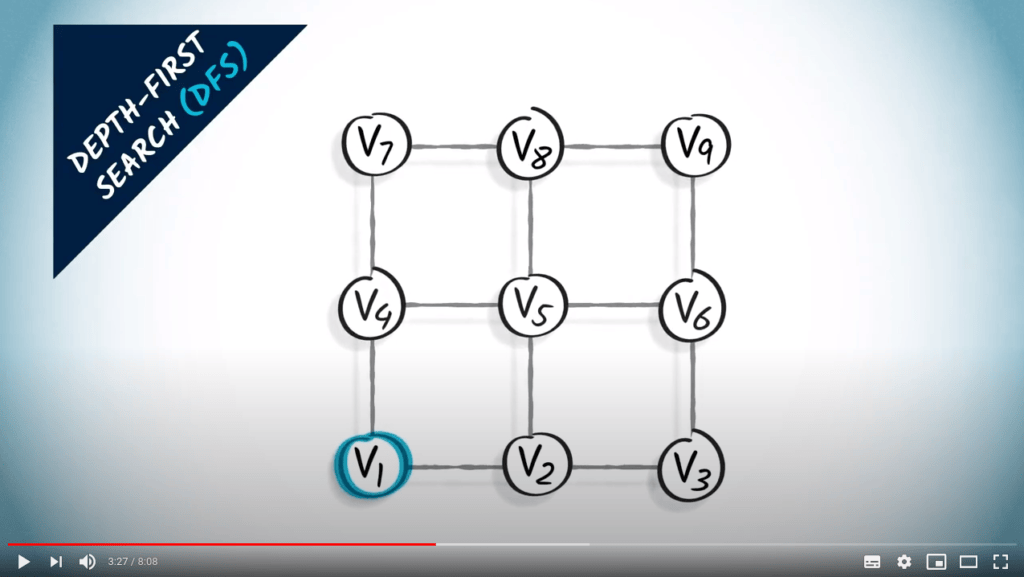
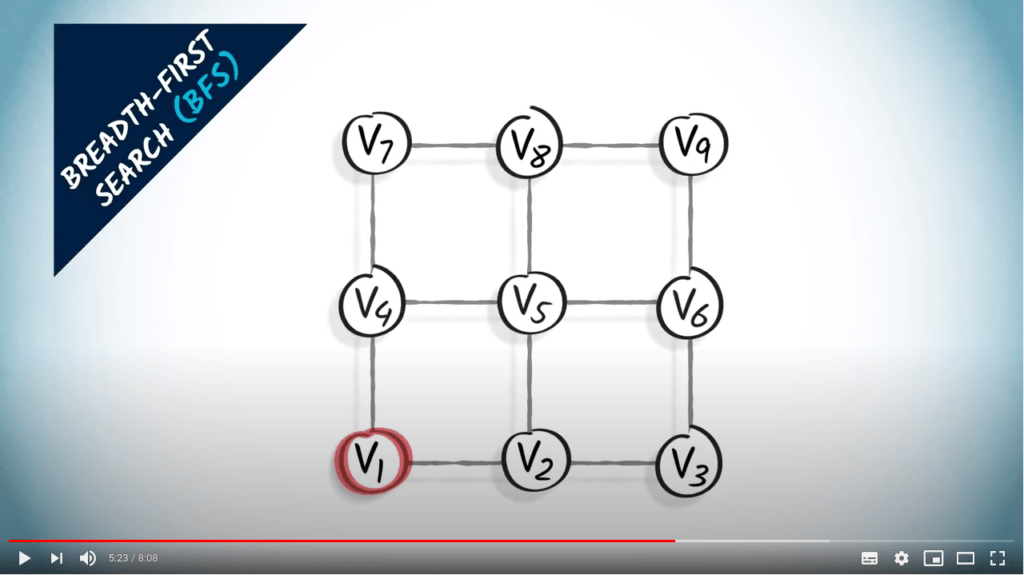
Parcours de graphes
Deux stratégies sur un graphe non pondéré
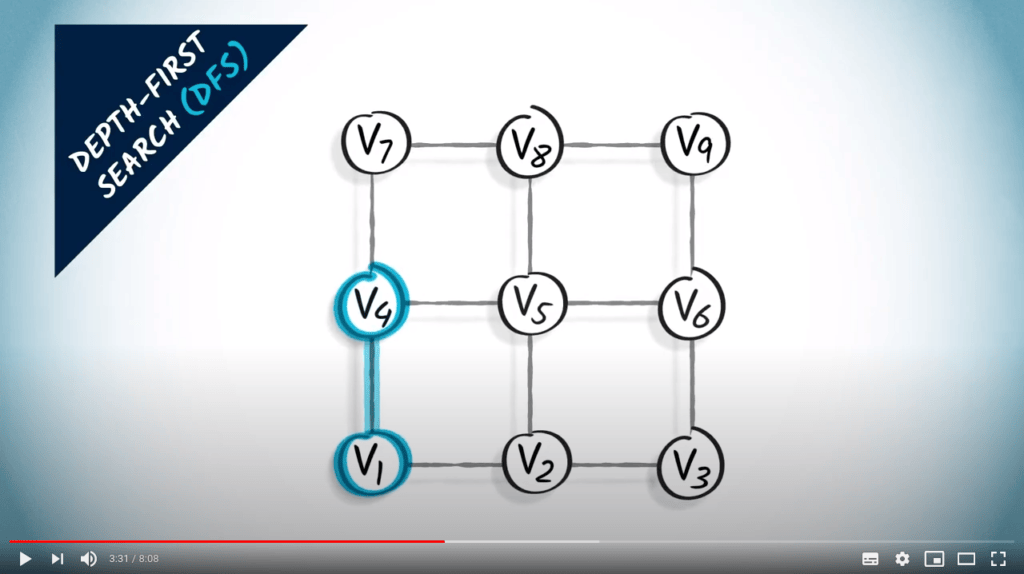
Parcours de graphes
Deux stratégies sur un graphe non pondéré
Parcours de graphes
Deux stratégies sur un graphe non pondéré
Parcours de graphes
Deux stratégies sur un graphe non pondéré
Parcours de graphes
Deux stratégies sur un graphe non pondéré

Parcours de graphes
Deux stratégies sur un graphe non pondéré

Parcours de graphes
Deux stratégies sur un graphe non pondéré

Parcours de graphes
Deux stratégies sur un graphe non pondéré
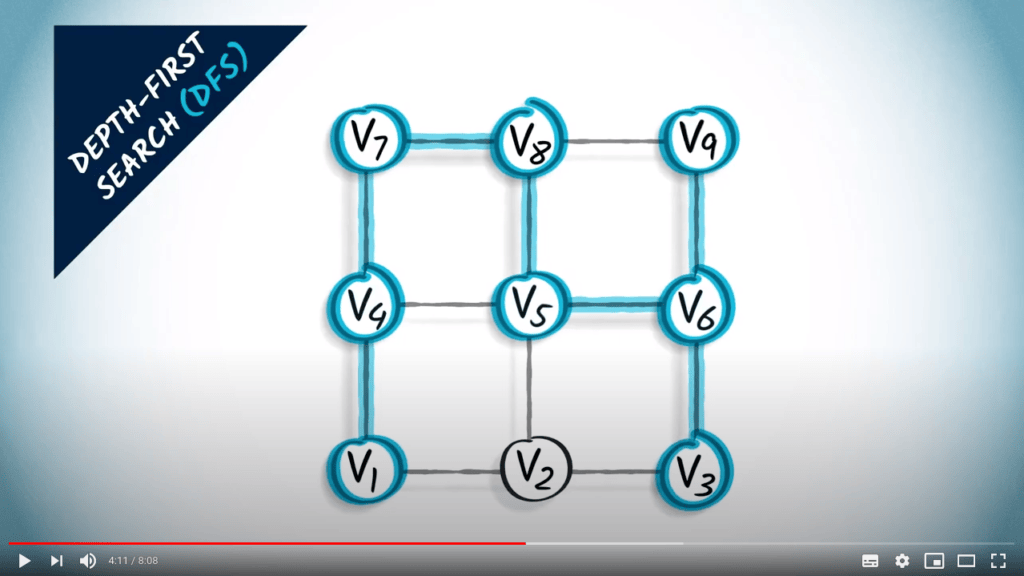

Parcours de graphes
Deux stratégies sur un graphe non pondéré
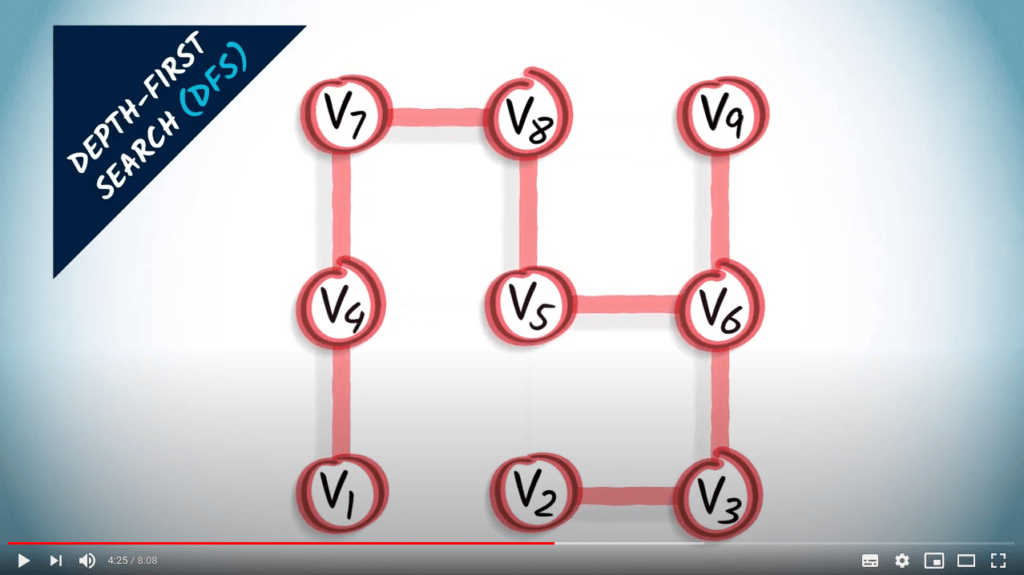
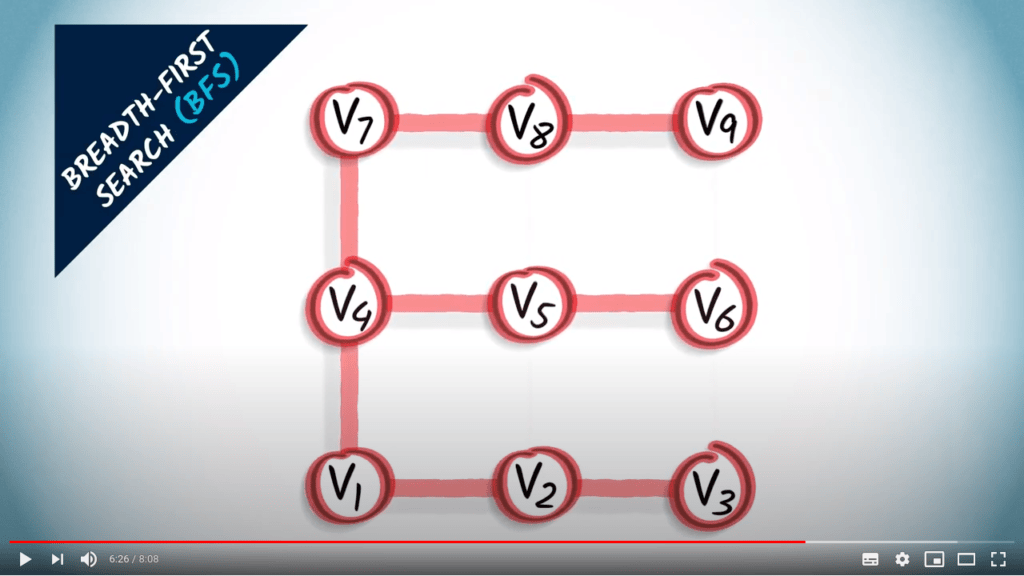
- Un parcours correspond à un arbre couvrant du graphe
- BFS trouve le plus court chemin de $v_1$ à tous les autres sommets
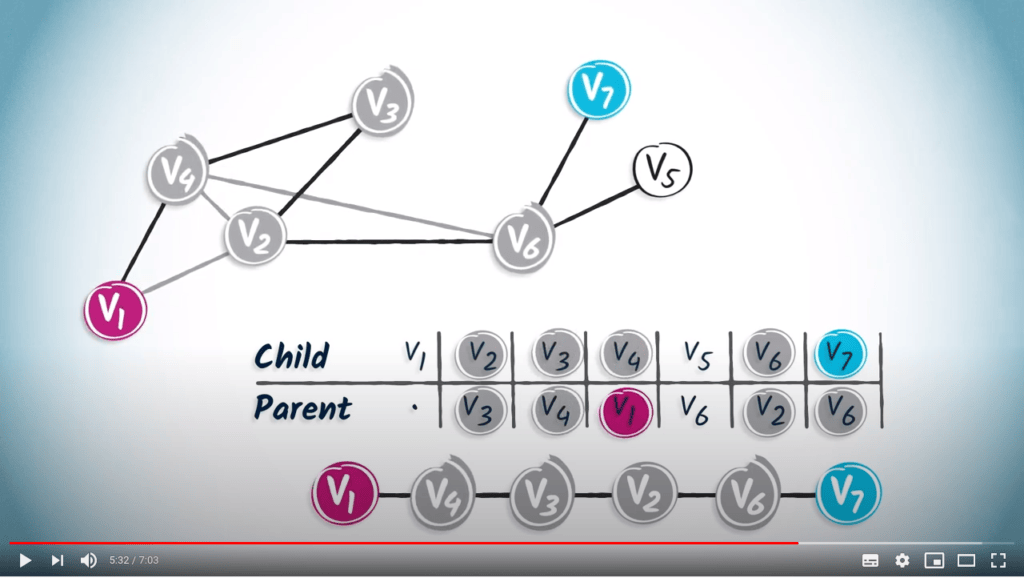
Tables de routage
Une manière de stocker l’arbre couvrant en mémoire
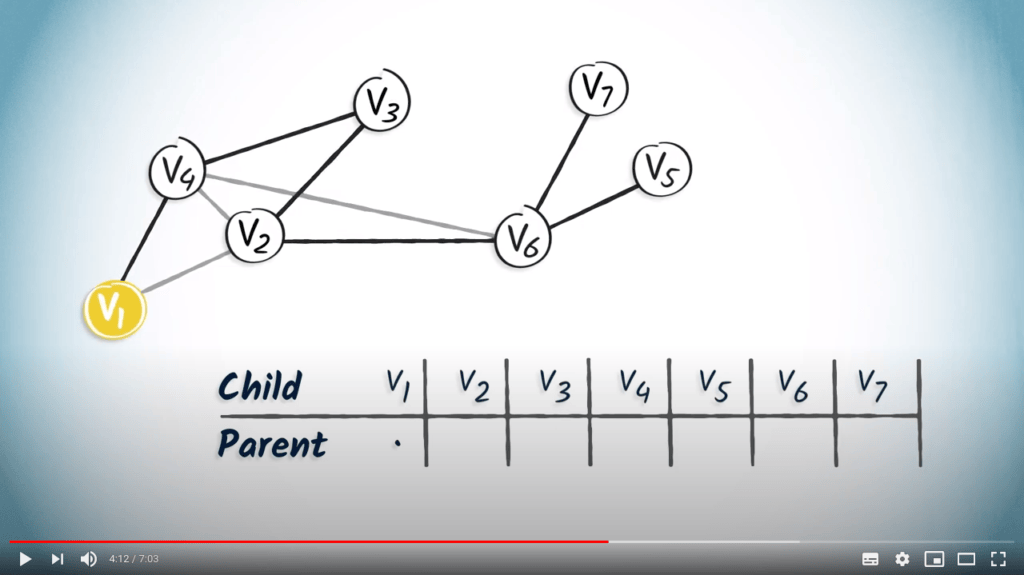
Tables de routage
Une manière de stocker l’arbre couvrant en mémoire
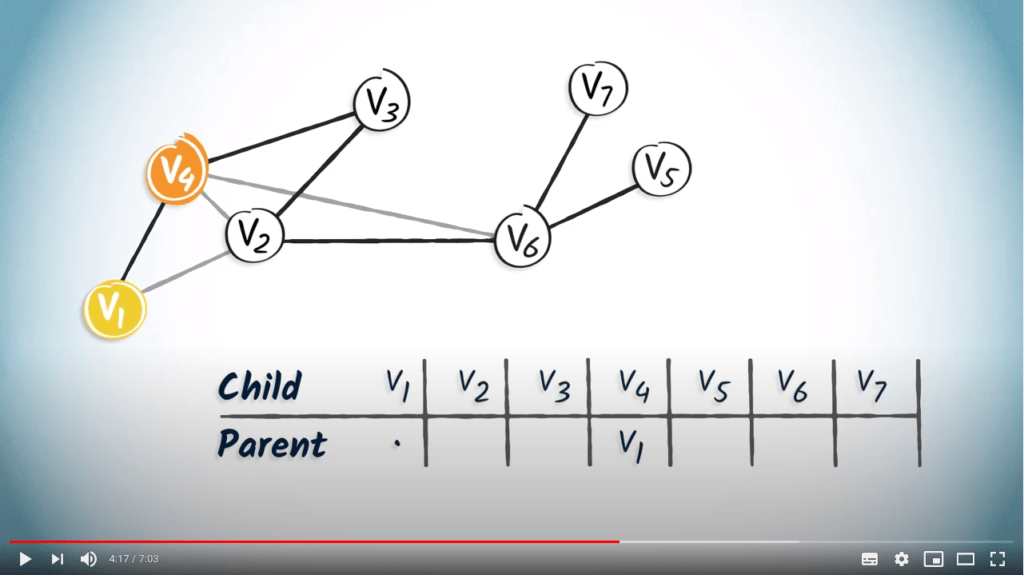
Tables de routage
Une manière de stocker l’arbre couvrant en mémoire
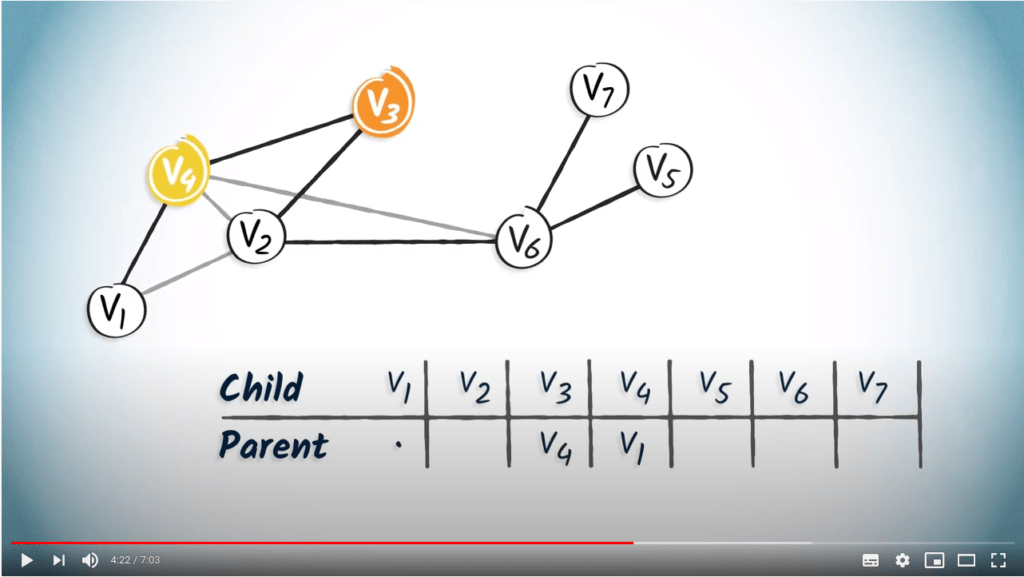
Tables de routage
Une manière de stocker l’arbre couvrant en mémoire
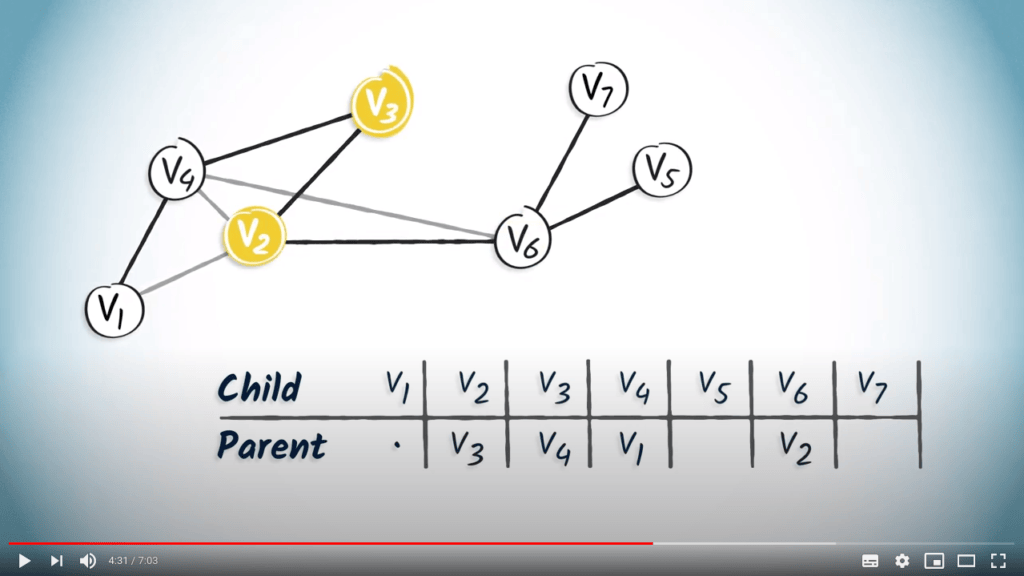
Tables de routage
Une manière de stocker l’arbre couvrant en mémoire
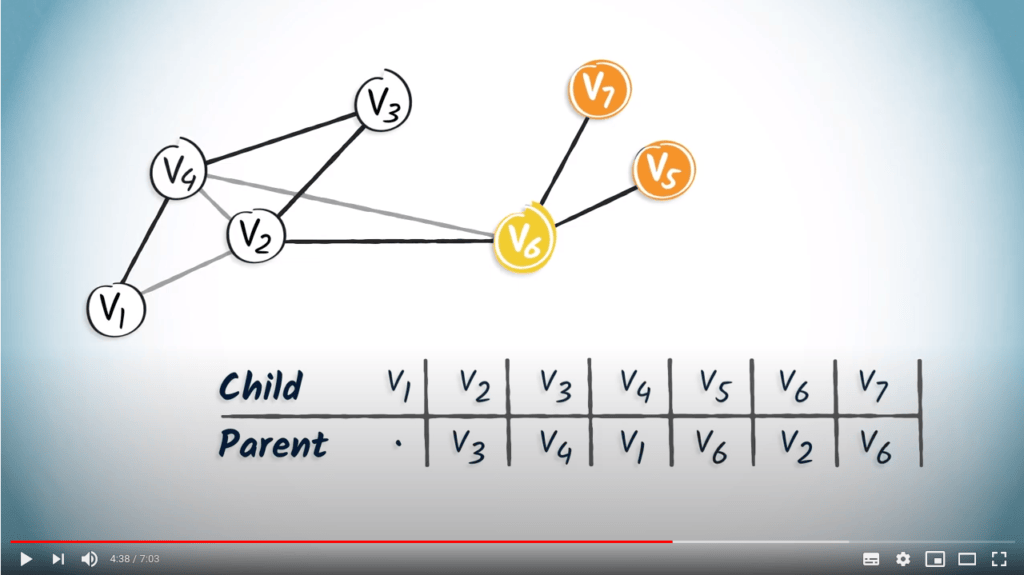
Tables de routage
Récupérer le plus court chemin
Structures de file pour les parcours de graphes
Files / Premier entré premier sorti / FIFO

- Les éléments entrent et sortent de la structure dans le même ordre
- Adapté à un BFS
Structures de file pour les parcours de graphes
Piles / Dernier entré premier sorti / LIFO

- Les premiers éléments à entrer dans la structure sont les derniers à en sortir
- Adapté à un DFS
Structures de file pour les parcours de graphes
Un algorithme unifié
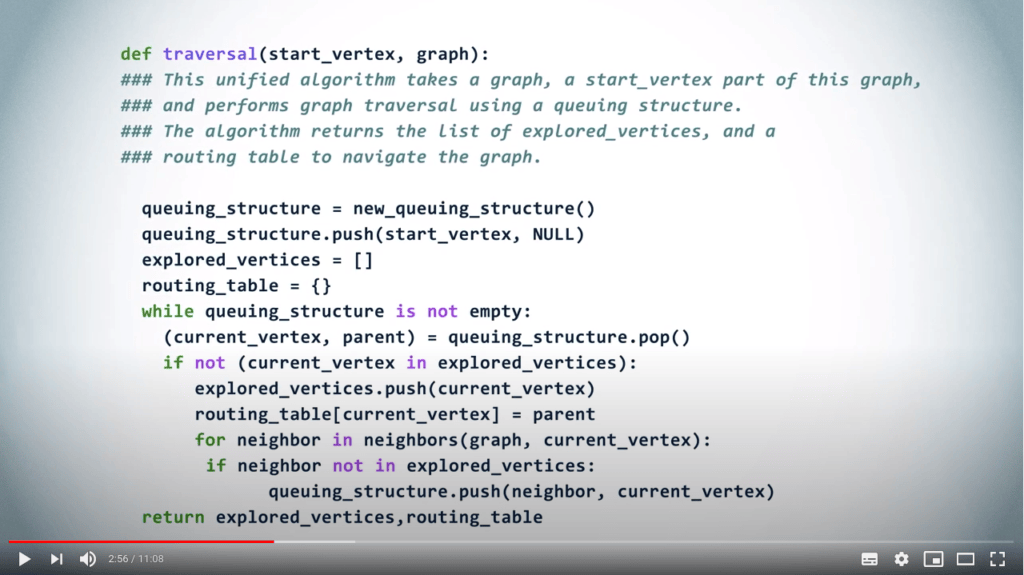
- Le parcours effectué dépend de l’ordre dans lequel les voisins sont explorés
- La structure de données utilisée détermine cet ordre
Récapitulatif de la session
Éléments principaux à retenir
-
Pour aborder un problème : formaliser, spécifier, puis coder
-
La théorie des graphes fournit une modélisation abstraite des éléments d’intérêt et de leurs relations
-
Les parcours sont des algorithmes conçus pour explorer un graphe
-
BFS est une stratégie qui trouve le plus court chemin dans un graphe non pondéré
-
Les structures de données ont leurs propriétés, qui peuvent être exploitées par les algorithmes
Récapitulatif de la session
Et après ?
Activité pratique (~2h30)
Attraper un fromage
- Programmer un DFS
- Programmer un BFS
- Comparer les algorithmes
Après la session
- Revoir les articles de la session
- Vérifier votre compréhension avec le quiz
- Compléter l’activité pratique
- Consulter la section “Avant le cours” de la prochaine session
Évaluation
- Quiz évalué pour commencer la prochaine session !