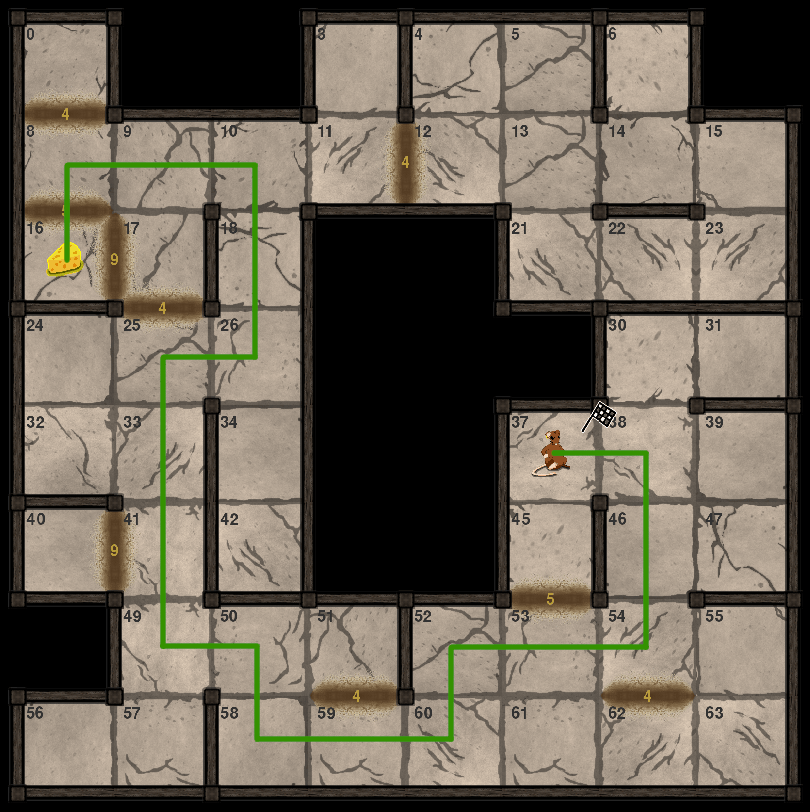
Catch a single piece of cheese… with mud
Project – Session 3
- L’algorithme de Dijkstra
- Tas minimum (min-heaps)
- Récapitulatif de la session
Dijkstra’s algorithm
Trouver le chemin le plus court dans un graphe pondéré

Dijkstra’s algorithm
Une application directe de l’algorithme BFS

Dijkstra’s algorithm
Le véritable chemin le plus court
Dijkstra’s algorithm
Comment ça marche ?
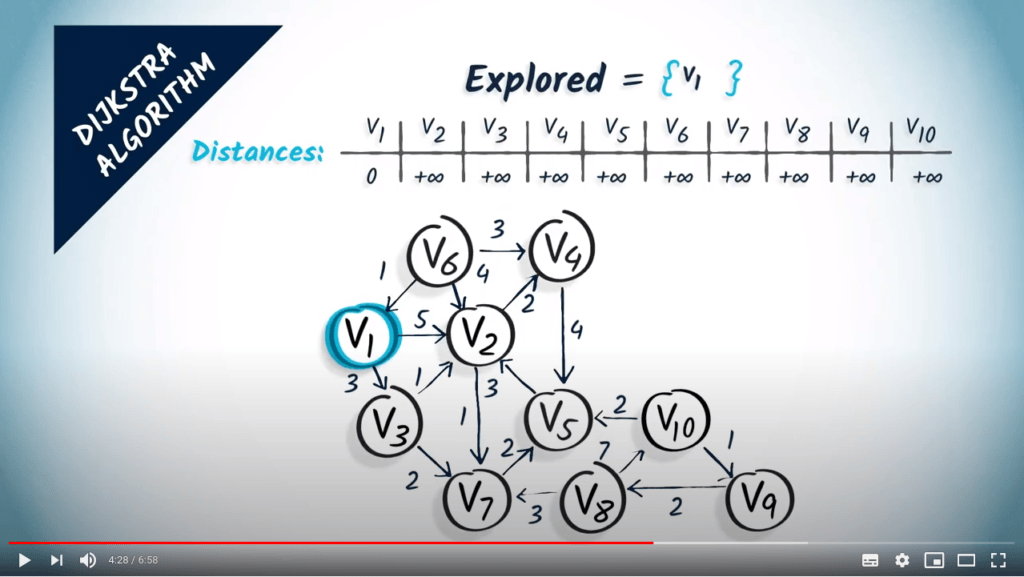
- Initialiser un tableau de distances à $+\infty$ pour le sommet initial $v_1$
- Initialiser un ensemble pour mémoriser quels sommets ont été explorés
Dijkstra’s algorithm
Comment ça marche ?
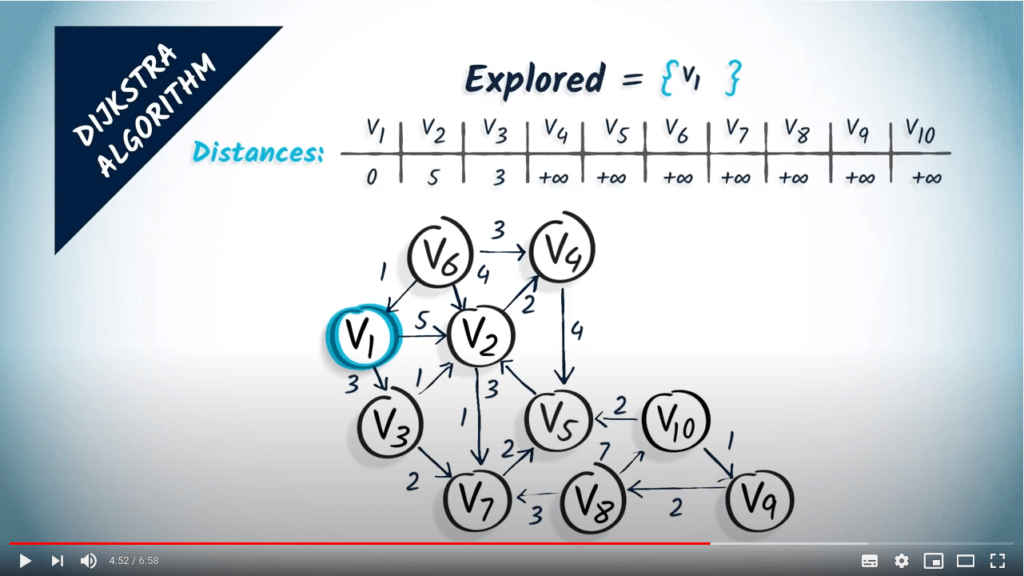
- Mettre à jour les distances vers les voisins accessibles
- Nous mettons à jour $v_2$ (distance de $5 < +\infty$) et $v_3$ (distance de $3 < +\infty$)
Dijkstra’s algorithm
Comment ça marche ?
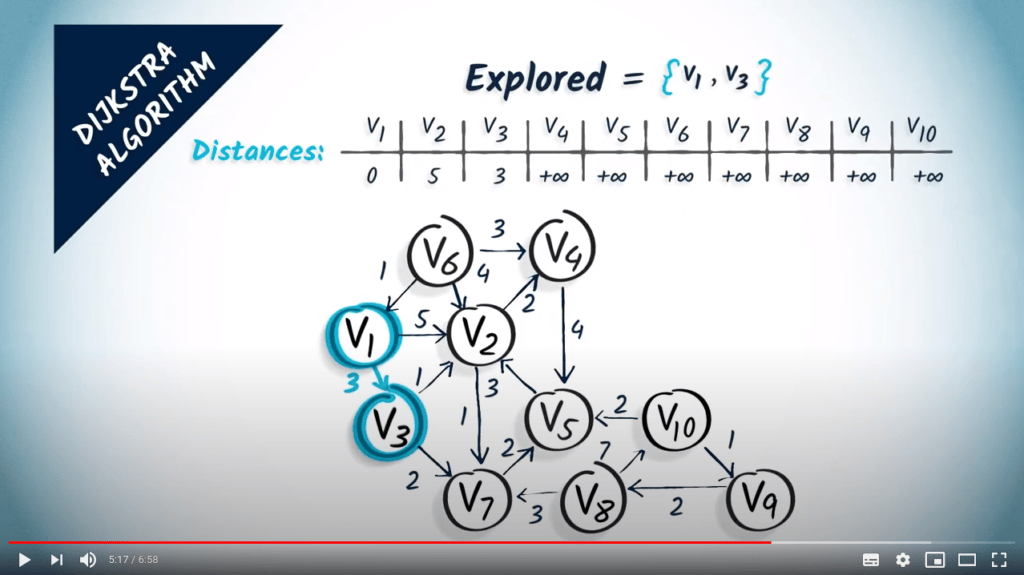
- Explorer le voisin non visité avec la distance minimale vers $v_1$
- Nous explorons $v_3$
Dijkstra’s algorithm
Comment ça marche ?
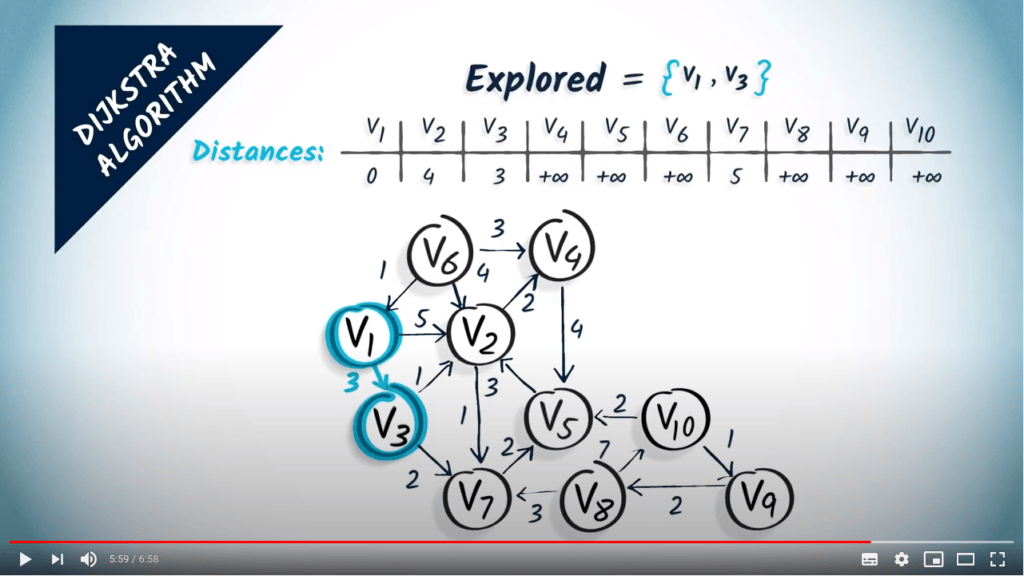
- Mettre à jour les distances vers les voisins accessibles
- Nous mettons à jour $v_2$ (distance de $3+1 < 5$) et $v_7$ (distance de $3+2 < +\infty$)
Dijkstra’s algorithm
Comment ça marche ?
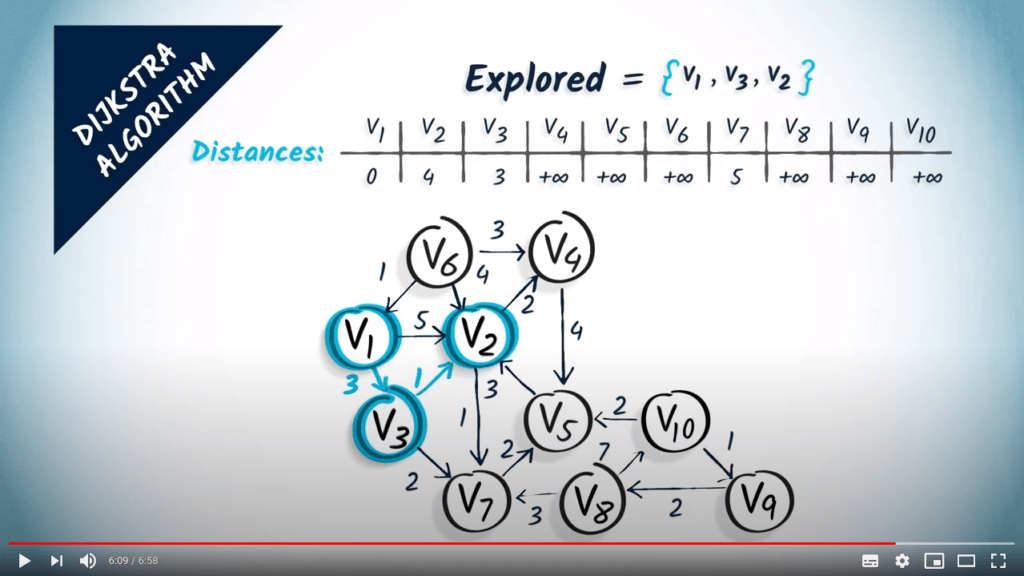
- Explorer le voisin non visité avec la distance minimale vers $v_1$
- Nous explorons $v_2$
Dijkstra’s algorithm
Comment ça marche ?
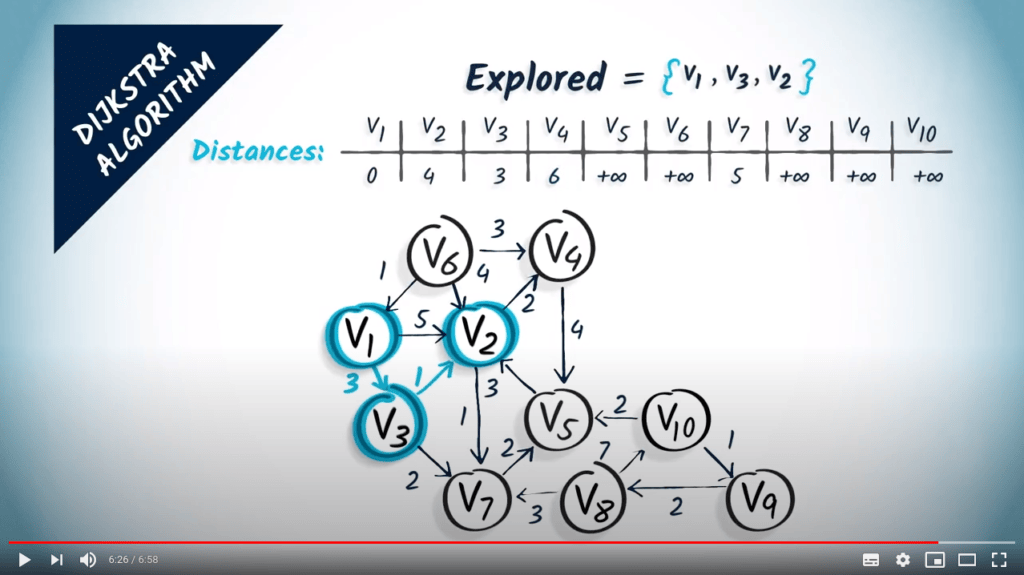
- Mettre à jour les distances vers les voisins accessibles
- Nous mettons à jour $v_4$ (distance de $3+1+2 < +\infty$)
Dijkstra’s algorithm
Comment ça marche ?
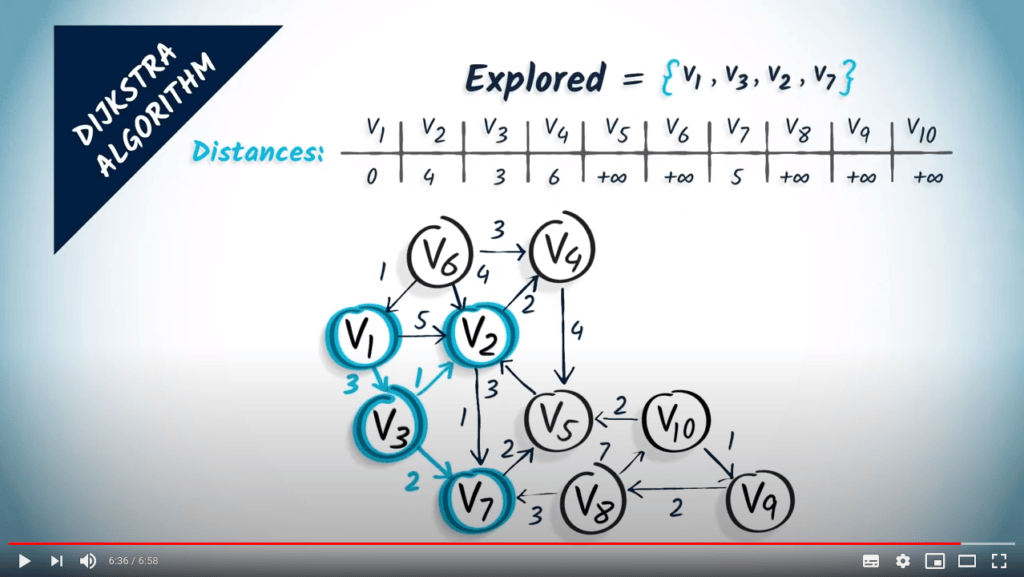
- Explorer le voisin non visité avec la distance minimale vers $v_1$
- Nous explorons $v_7$, aucune distance à mettre à jour
Dijkstra’s algorithm
Comment ça marche ?

- Explorer le voisin non visité avec la distance minimale vers $v_1$
- Nous explorons $v_5$, aucune distance à mettre à jour, nous avons terminé !
Min-heaps
Utiliser un tas minimum
-
Tout comme les FIFOs et LIFOs, les tas minimum stockent des éléments
-
Deux méthodes :
pushstocke un élément dans la structurepopextrait le plus petit élément
-
“plus petit” doit être précisé
# Create a min-heap
heap = new_heap()[]# Add elements to the heap
push(heap, ("A", 50))
push(heap, ("B", 22))
push(heap, ("C", 10))[('A', 50), ('B', 22), ('C', 10)]# Extract smallest element from the heap
pop(heap)('A', 50)Min-heaps
L’algorithme de Dijkstra et les tas minimum

- Explorer le voisin non visité avec la distance minimale vers $v_1$
- Maintenir un tas minimum avec des éléments (distance vers $v_1$, $v_x$)
Recap of the session
Éléments principaux à retenir
-
L’algorithme de Dijkstra étend BFS aux graphes pondérés
-
Pensez à l’eau qui coule à travers le graphe à vitesse constante
-
Nous n’avons pas parlé des tables de routage mais vous en aurez besoin pour récupérer le chemin
-
Les tas minimum sont des structures de données qui extraient l’élément minimum
-
De nombreuses implémentations sont possibles, attention aux détails !
-
L’algorithme de Dijkstra est un parcours qui exploite les propriétés d’un tas minimum
-
Rappelez-vous la relation entre BFS/queue et DFS/stack
Recap of the session
Et après ?
Activité pratique (~2h30)
Attraper un fromage avec de la boue
- Programmer l’algorithme de Dijkstra
- Réfléchir soigneusement aux structures de données
Après la session
- Revoir les articles de la session
- Vérifier votre compréhension avec le quiz
- Compléter l’activité pratique
- Consulter la section “Avant le cours” de la prochaine session
Évaluation
- Quiz évalué pour commencer la prochaine session !
- Livrable pour la session 3 (voir la page de la session pour les détails)