Catch multiple pieces of cheese
Project – Session 4
- Complexité des algorithmes
- Complexité des problèmes & NP-complétude
- Le problème du voyageur de commerce
- Bruteforce & backtracking pour résoudre les problèmes NP-complets
Algorithm complexity
How to compare algorithms efficiency?
Mesurer le temps d’exécution
- Nécessite d’exécuter le programme
- Dépend du matériel, du langage de programmation, des autres processus en cours…
Quelque chose de plus abstrait : la complexité
- Nombre d’opérations en fonction de la taille de l’entrée $n$
- On utilise la notation $O(\cdot)$, ex., $O(n)$, $O(n^2)$, $O(n!)$
$\rightarrow$ Indépendant du matériel, du langage de programmation…
$\rightarrow$ Ne nécessite pas d’exécuter le programme
- Exemples – DFS/DFS : $O(|E|)$ ; Dijkstra : $O(|E| + |V| \cdot log(|V|))$
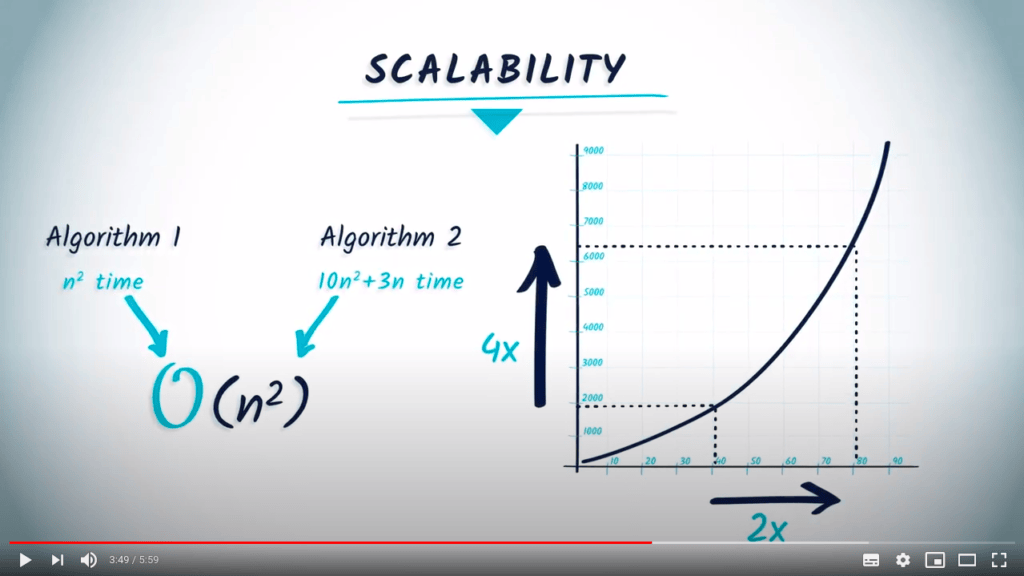
Algorithm complexity
Comparing algorithms using complexity
$$O(n) < O(n^2)$$
$$O(n) = O(123456789 \cdot n)$$
$$O(n^2) = O(n^2 + n)$$
$$O(n^{10000}) < O(n!)$$
$$O(n) = O(123456789 \cdot n)$$
$$O(n^2) = O(n^2 + n)$$
$$O(n^{10000}) < O(n!)$$
Remarques
- Comparer le comportement asymptotique
- On s’intéresse à la complexité dans le pire cas, c’est-à-dire l’estimation dans le cas le moins favorable
Problem complexity & NP-completeness
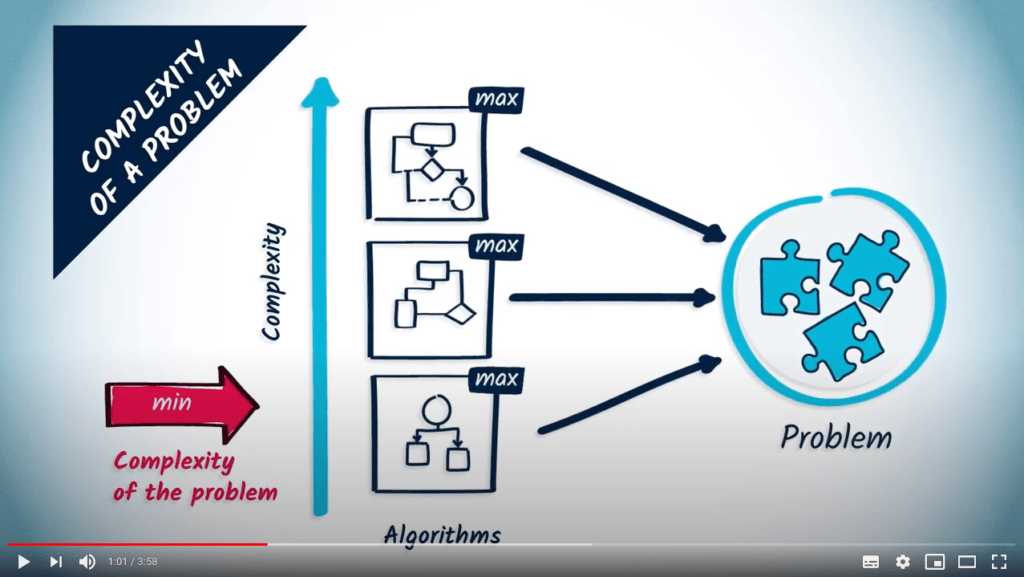
From algorithm complexity to problem complexity
La complexité d’un problème est la complexité minimale des algorithmes qui résolvent ce problème
Problem complexity & NP-completeness
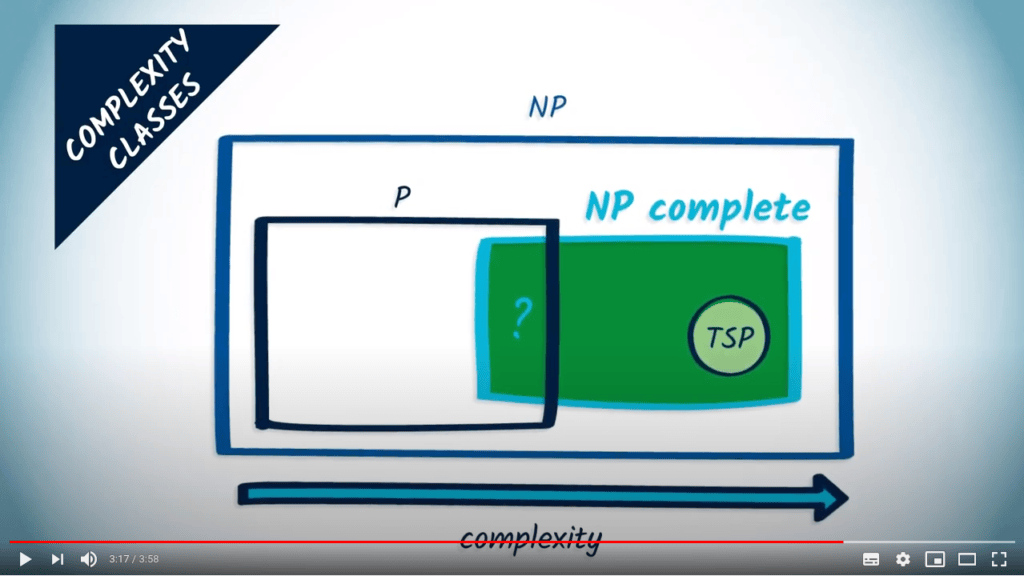
Complexity classes
- Classes d’équivalence entre algorithmes et problèmes
- Dijkstra, BFS, DFS sont des algorithmes polynomiaux pour trouver des chemins (problèmes de la classe P)
- Certains problèmes ne peuvent pas être résolus par un algorithme polynomial connu, ex., le problème du voyageur de commerce (problème NP-complet)
The traveling salesman problem
Problem description
Trouver le chemin le plus court qui passe par tous les emplacements
The traveling salesman problem
Step 1: abstract useless details
Trouver le chemin le plus court qui passe par tous les sommets d’un graphe complet
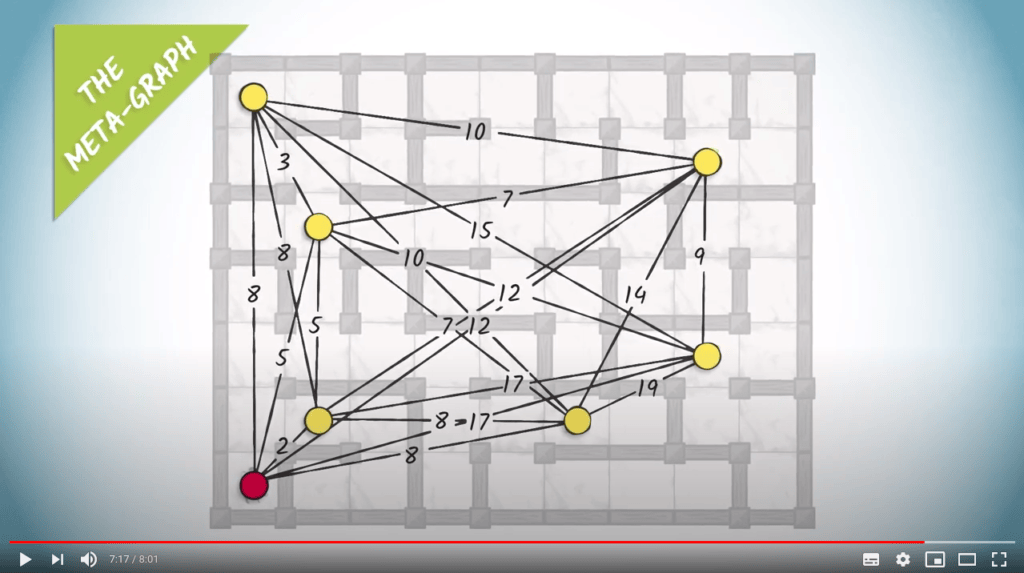
Bruteforce & backtracking to solve NP-complete problems
Step 2: test every permutation
- Note – Cela revient à effectuer un DFS par branche
Bruteforce & backtracking to solve NP-complete problems
Step 2 (alternative): test (nearly) every permutation
- Le nombre de branches sautées dépend de la qualité des premières explorées
- Cela ne change pas la complexité (dans le pire cas)
Recap of the session
Main elements to remember
-
Les algorithmes peuvent être comparés selon leur complexité
-
La complexité d’un problème est déterminée par le meilleur algorithme pour le résoudre
-
Il existe des problèmes très difficiles à résoudre, comme le TSP
-
Ces problèmes ne peuvent être résolus qu’en testant toutes les solutions possibles
Recap of the session
What’s next?
Activité pratique (~2h30)
Attraper plusieurs morceaux de fromage
- Programmer le TSP (+ backtracking)
- Utiliser Dijkstra ou BFS comme base
Après la séance
- Revoir les articles de la séance
- Vérifier votre compréhension avec le quiz
- Compléter l’activité pratique
- Consulter la section “Avant le cours” de la prochaine séance
Évaluation
- Quiz évalué pour commencer la prochaine séance !