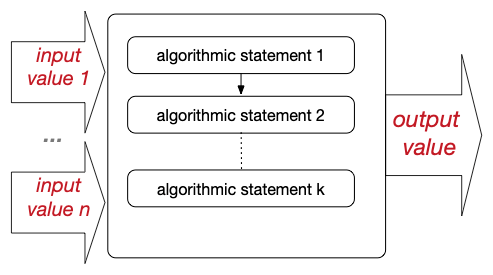
• An algorithm is a solution to a specific problem that takes a set of values as input and produces a value as a result

• This solution is realised by a sequence of algorithmic statements applied to the input data to produce the final result value

Values

• 34, 1.09, “IMT Atlantique” or false are values that can be integrated into calculus

• For instance, 34 * 1.09 to get the conversion into euros of 34 dollars using a rate of 1.09

Variables

• Variables are names that refer to values, while constants are fixed

• Always favor variables over reuses of the same value

• Values have an associated type, which defines possible operations on them

• Programming languages define several elementary types (booleans, integers, real numbers, strings, etc.) and allow us to create your own composite types

• Data structures allow to group simple types into collections

Essential elements

• Defining variables / assigning values (e.g., a = 34 * nb)
• Operators on variables
• Conditions
• Loops

A bit of sugar

• Defining / calling functions (programming session 2)
• Object-oriented programming (programming session 4)

Conditions

Conditional statements (if) are used to split the sequential execution of the algorithm based on a Boolean condition:

if estimated_value - real_value < epsilon: 
    print("Estimation found:", estimated_value)
else:
    print("Continuation")

A few alternate syntaxes (see match doc):

if est - real < eps: 
    print("Estimation found:", est)
elif est - real < 2 * eps: 
    print("Less precise:", est)
else:
    print("Continuation")

match est - real:
    case 0 | 2 | 4: print("Even difference")
    case 6 | 8:     print("Higher even difference")
    case 3:         print("Difference of 3")
    case float():   print("Real difference")
    case  _ :       print("Something else")

Loops

Loops make it possible to define cycles in the execution flow of an algorithm

# Initialize a few variables
v = [1, 5, -5, 15, 0]
max_v = v[O] if len(v) > 0 else None

# A bounded loop
# Wll iterate len(v) times
for i in range(len(v)):
    if v[i] > max_v:
        max_v = v[i] 

# Initialize a few variables
v = [1, 5, -5, 15, 0]
max_v = v[O] if len(v) > 0 else None
i = 0

# An unbounded loop
# Will iterate until condition is false
while i < len(v):
    if v[i] > max_v:
        max_v = v[i] 
    i += 1

An invariant is used to prove by induction that a loop effectively reaches an expected state from an initial state

# This test should be true at any iteration of the loop
max_v == max(v[:i])

An algorithm is a solution to a specific problem that takes a set of values as input and produces a value as a result

• Algorithms are series of operations on variables, conditions and loops

• Unbounded loops can lead to infinite execution, so check your condition carefully

• Always favor variables over reuses of the same value

• Be aware of the types and mutabilities of variables