Catch a single piece of cheese
Project – Session 2
- Addressing a computational problem
- Graphs & paths
- Representing graphs
- Graph traversal
- Routing tables
- Queuing structures for graph traversals
- Recap of the session
Addressing a computational problem
Formalize

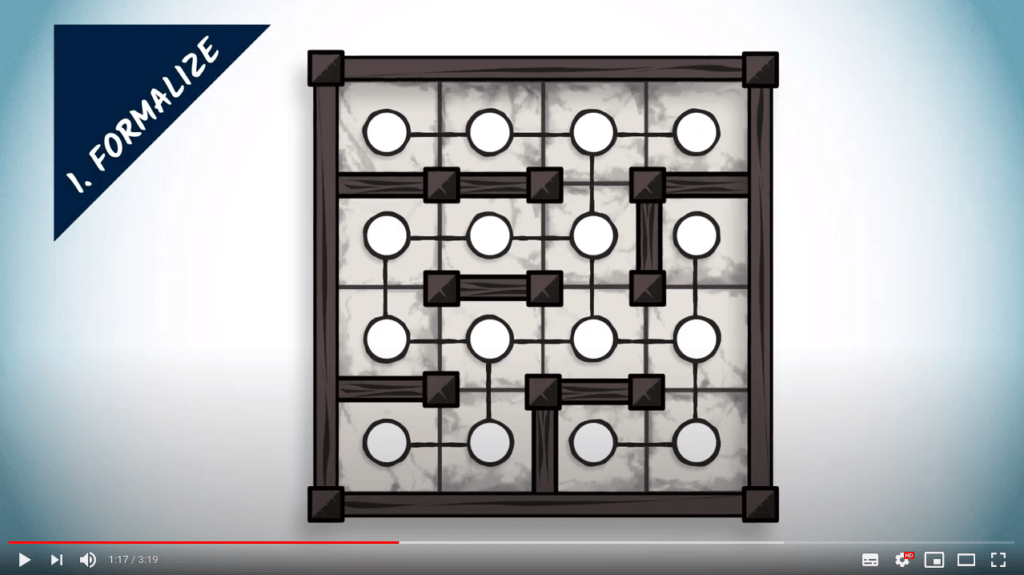
- Remove the details of the problems that are not necessary to solve it
- Find an adapted representation for the remaining elements
Addressing a computational problem
Specify
- Find an algorithm to solve the problem, given the chosen formalism
- Standard formalisms come with many algorithms
- Explore existing algorithms before reinventing the wheel!
Addressing a computational problem
Code
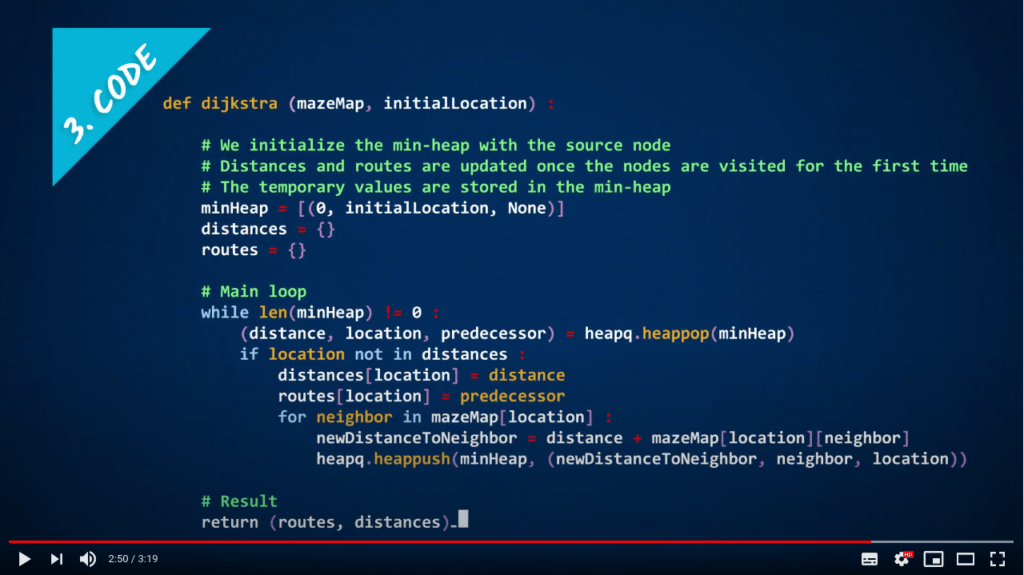
- Now that you have an algorithm, it’s time to implement it
- Again, before reinventing the wheel, check existing libraries!
Graphs & paths
What is a graph?

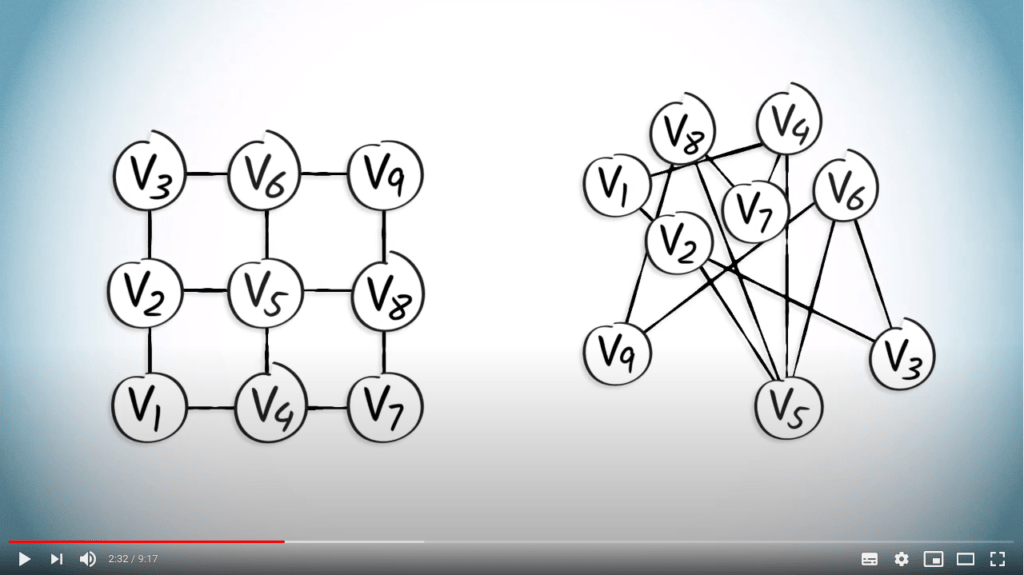
What is it?
- A mathematical abstraction of elements of interest and links between them
- E.g., Internet, connections in the brain, relations between variables, maze…
Formally
- Vertices $\mathcal{V}$ and edges $\mathcal{E}$
- Edges can be given a weight and a direction
- Graphical representation is not important, only edges count
Graphs & paths
Paths in graphs
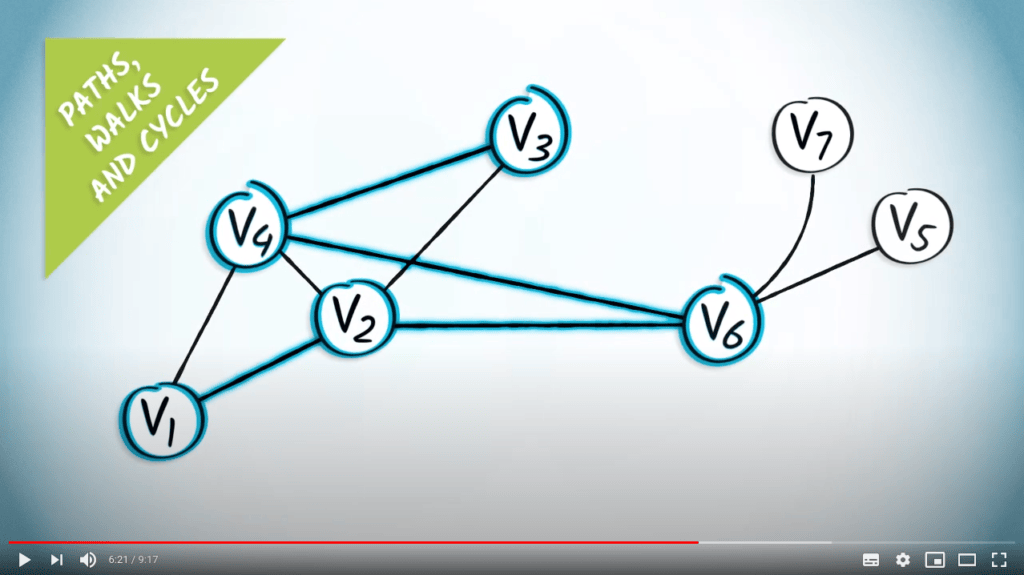
- A path is a series of edges without repetition of a vertex
- Paths do not contain cycles
- Length of a path is the sum of its weights (or number of edges if not weighted)
Representing graphs
The adjacency matrix
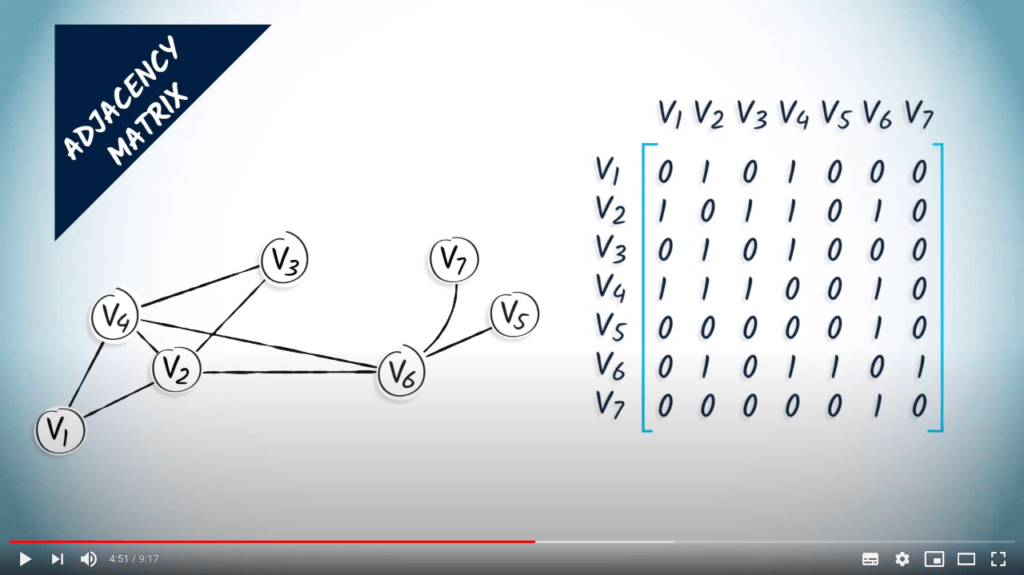
- How to store an adjacency matrix in memory? $\rightarrow$ array, list of lists, dictionary, object…
- In the PyRat software, an object provides ways to encode and manipulate the graph
Representing graphs
Details on the PyRat representation
Let g be an instance of Graph:
g.vertices # Gives you a list of vertices in the graph
g.nb_vertices # Gives you the number of vertices in the graph
g.edges # Gives you the list of edges in the graph
g.nb_edges # Gives you the number of edges in the graph
g.add_vertex(v) # Adds vertex v to the graph
g.add_edge(v1, v2, w) # Adds an edge of weight w between v1 and v2
g.get_neighbors(v) # Gives you the neighbors of v in the graph
g.get_weight(v1, v2) # Gives you the weight of edge between v1 and v2
g.remove_vertex(v) # Removes vertex v and all edges attached to it from the graph
g.remove_edge(v1, v2) # Removes edge between v1 and v2 from the graph
g.is_connected() # Indicates if the graph is connected
g.has_edge(v1, v2) # Indicates if an edge exists between vertices v1 and v2
g.edge_is_symmetric(v1, v2) # Indicates if edge from v1 to v2 can be used to go from v2 to v1
g.minimum_spanning_tree() # Gives you a minimum spanning tree for the graph
g.as_dict() # Gives you a dictionary representation of the graph
g.as_numpy_ndarray() # Gives you a matrix representation of the graph (as a numpy.ndarray)
g.as_torch_tensor() # Gives you a matrix representation of the graph (as a torch.tensor)In PyRat, you manipulate an instance of Maze, which inherits from Graph $\rightarrow$ More in class Maze!
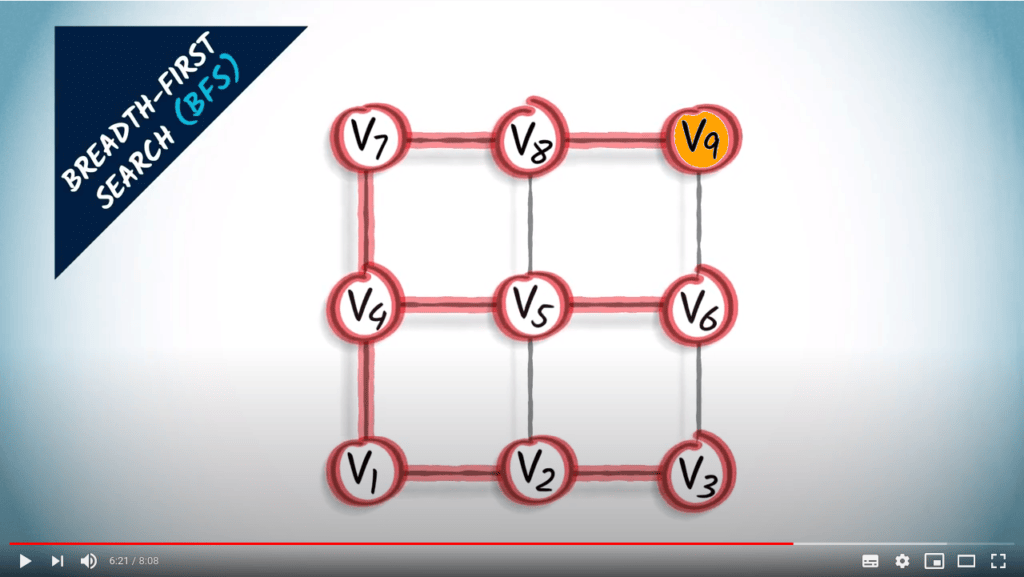
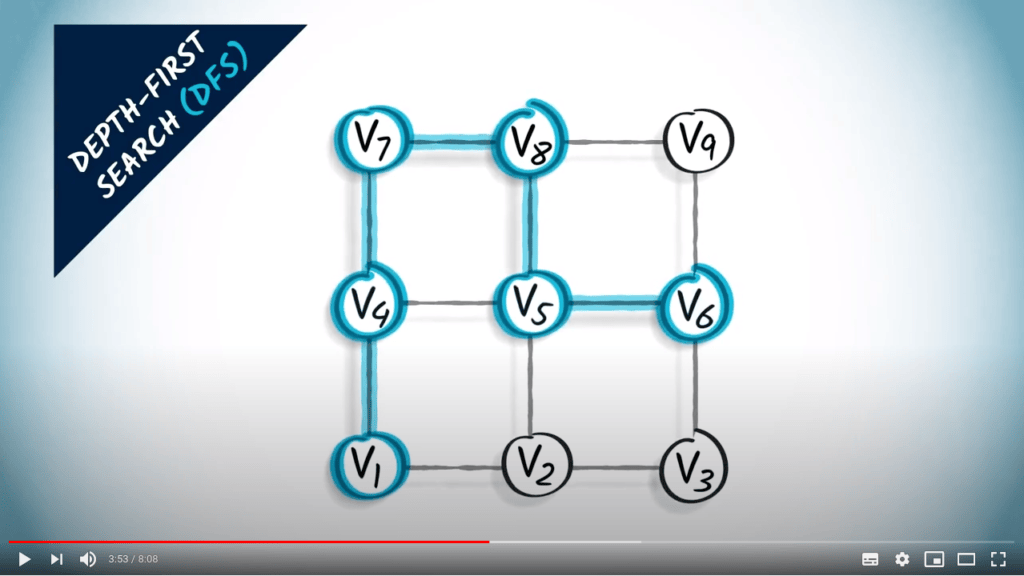
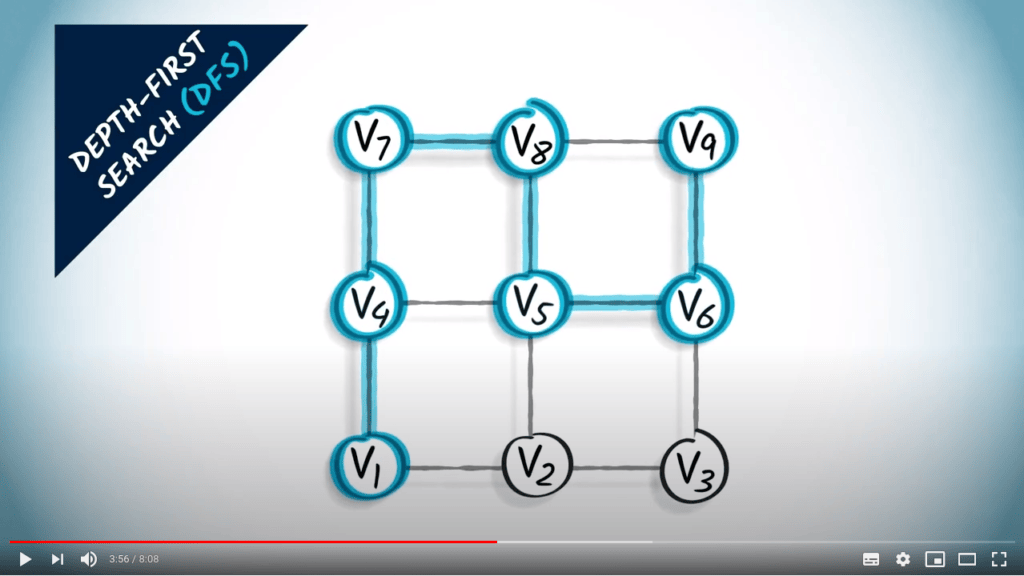
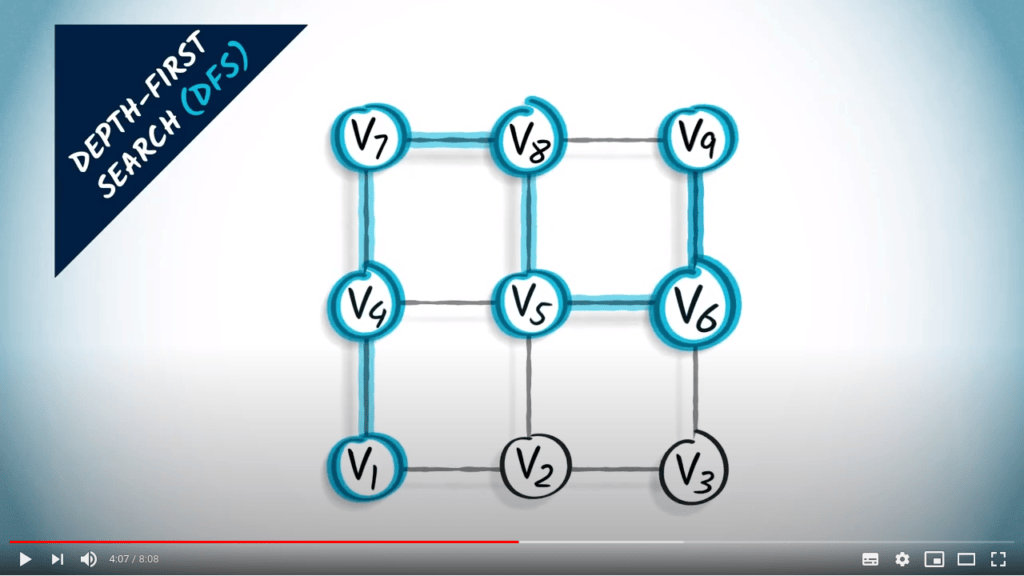
Graph traversal
What is a traversal?
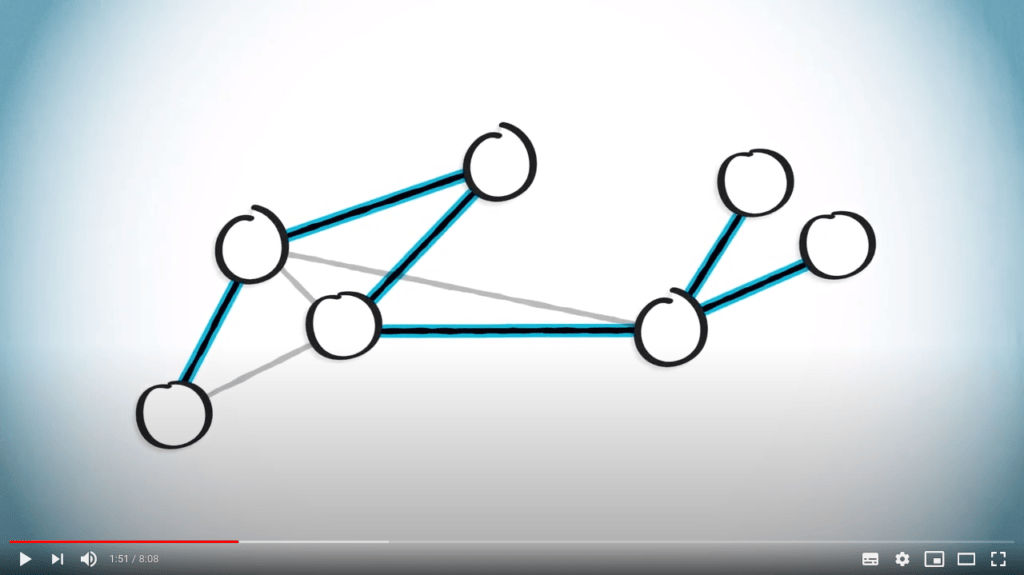
- A way to explore all vertices of a graph
- Start from a vertex, and iteratively go to its neighbors
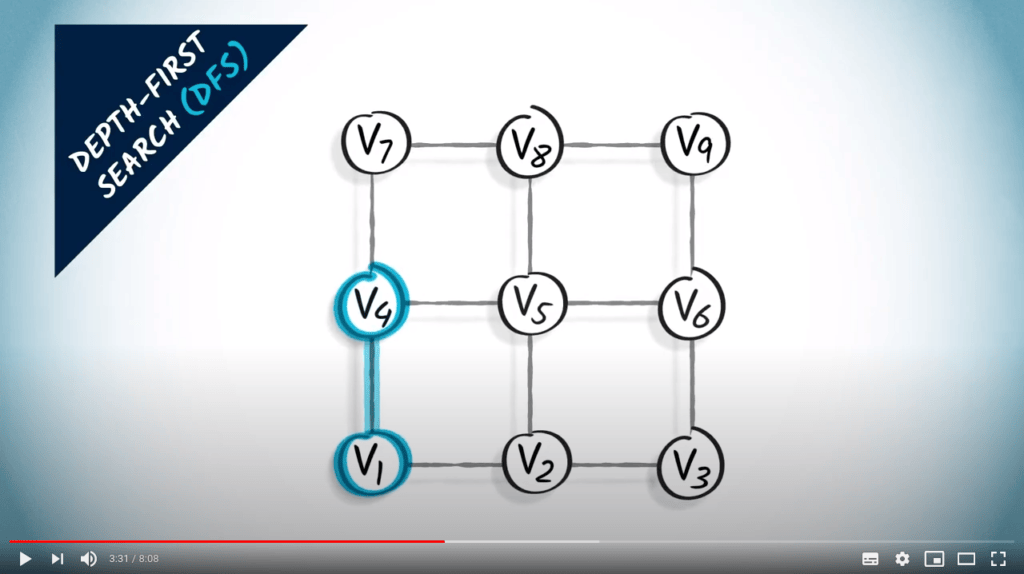
Graph traversal
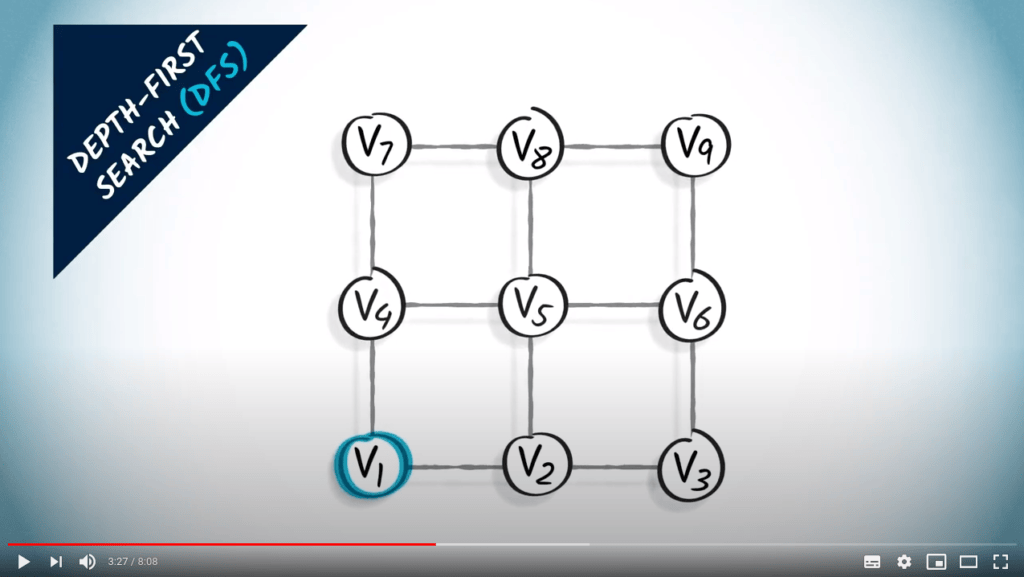
Two strategies on a non-weighted graph
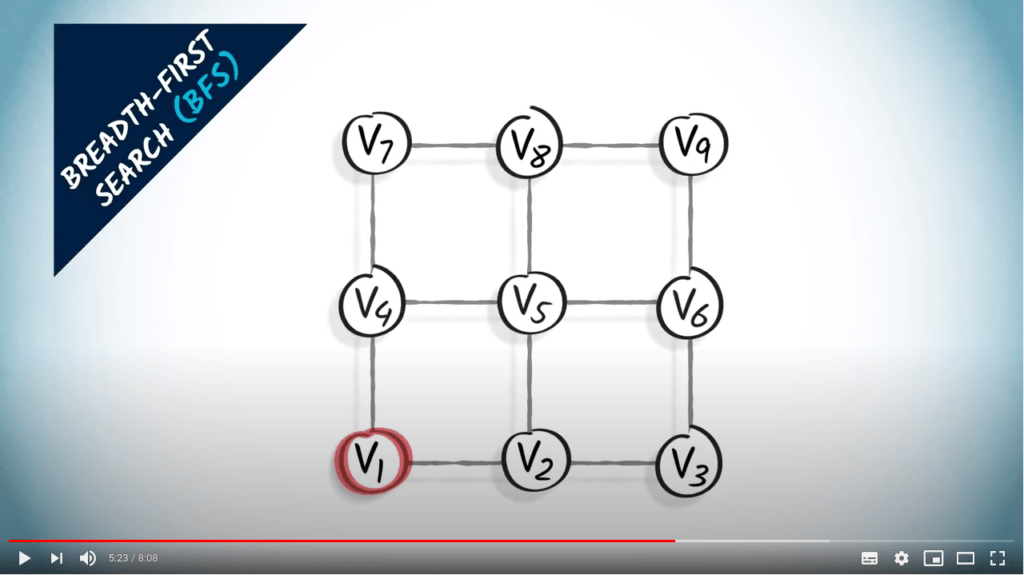
Graph traversal
Two strategies on a non-weighted graph
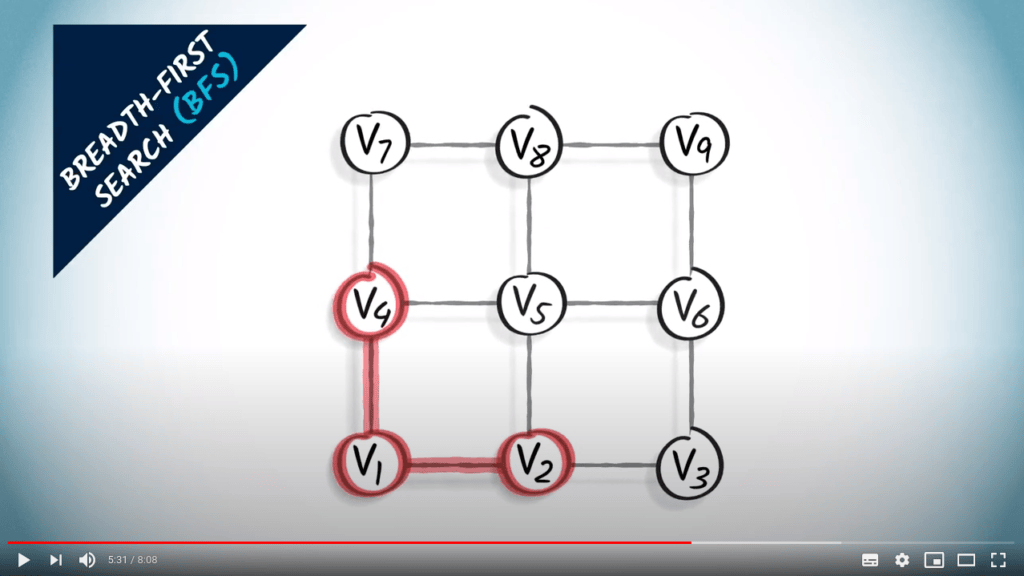
Graph traversal
Two strategies on a non-weighted graph
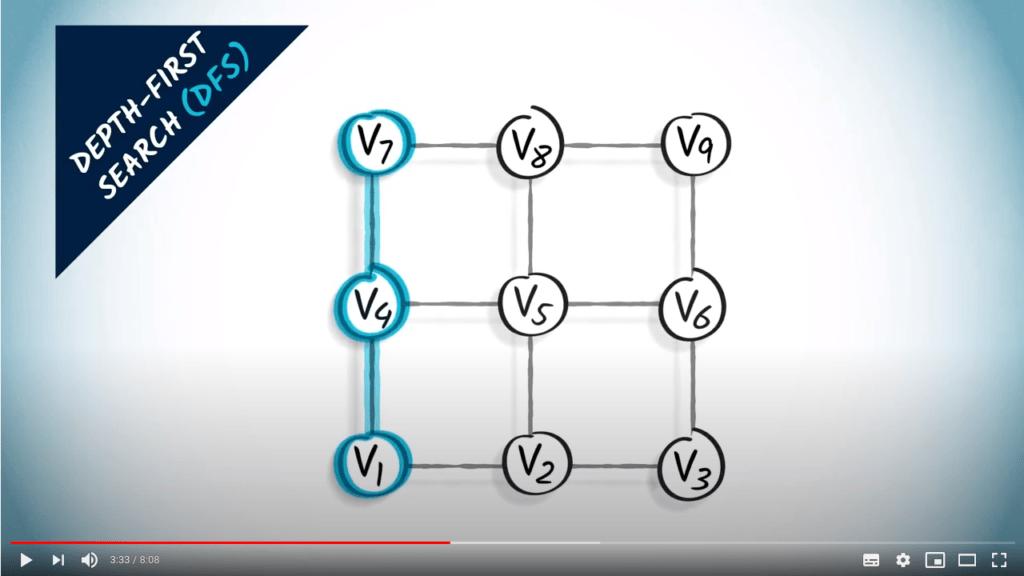
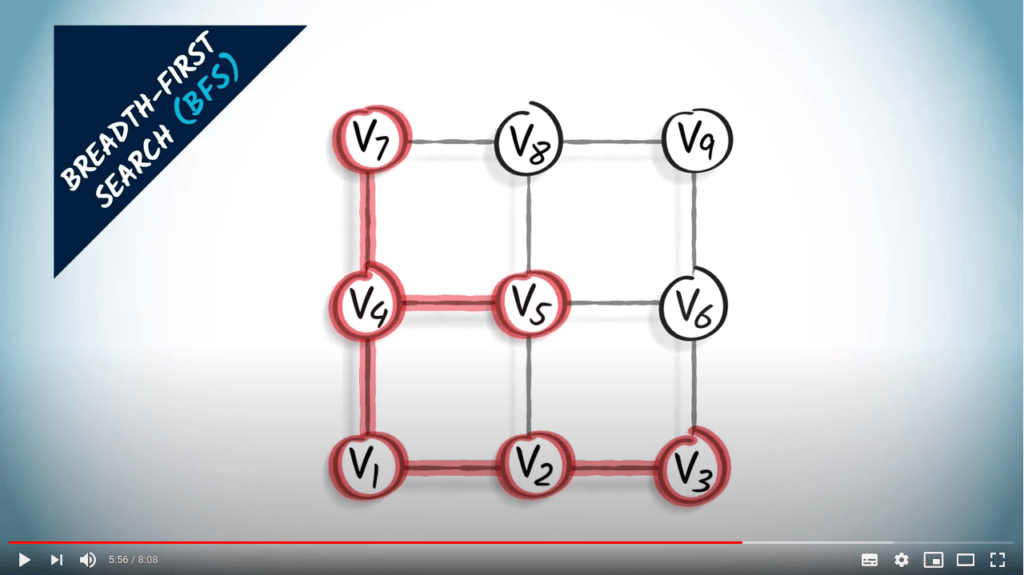
Graph traversal
Two strategies on a non-weighted graph
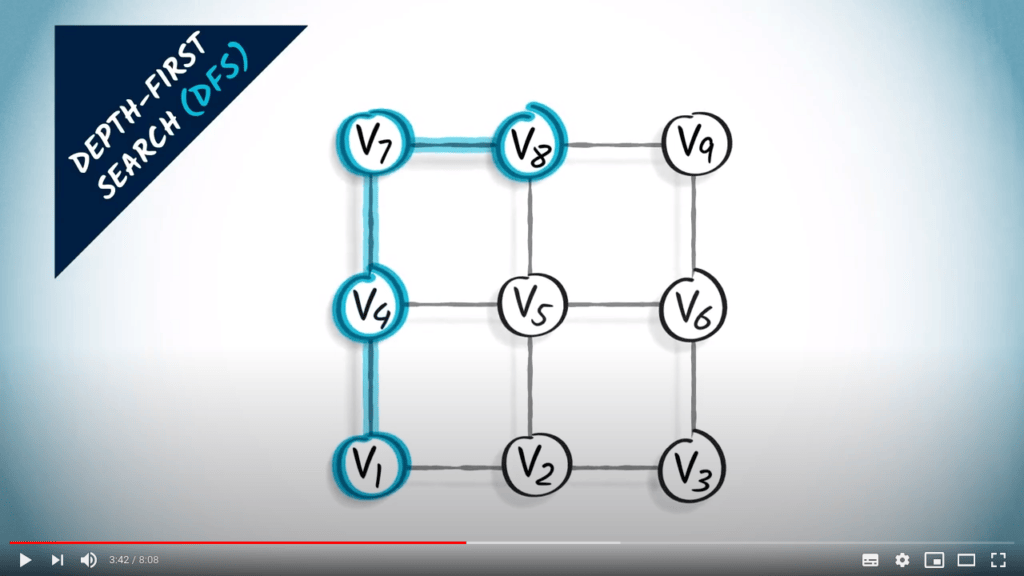
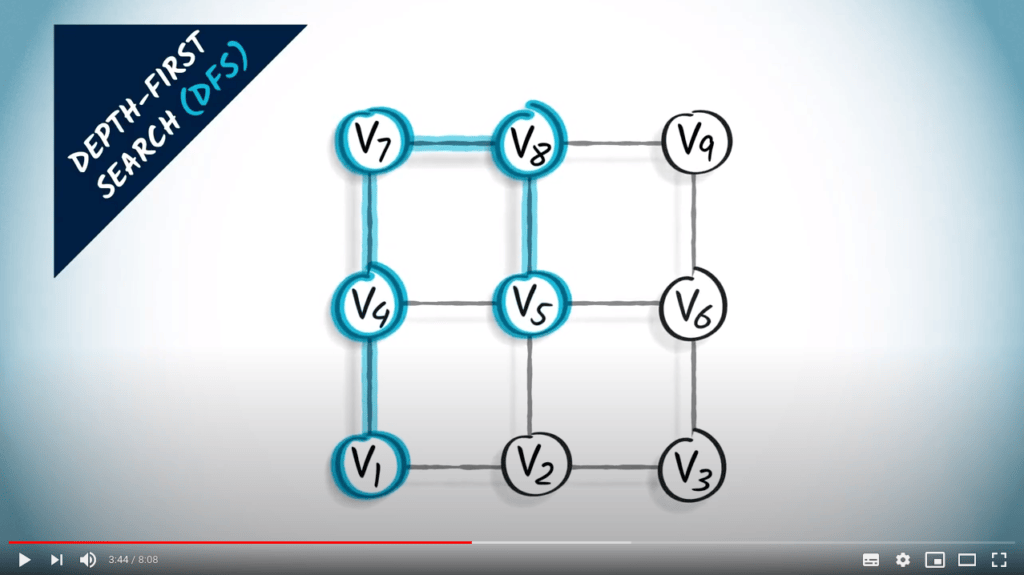
Graph traversal
Two strategies on a non-weighted graph
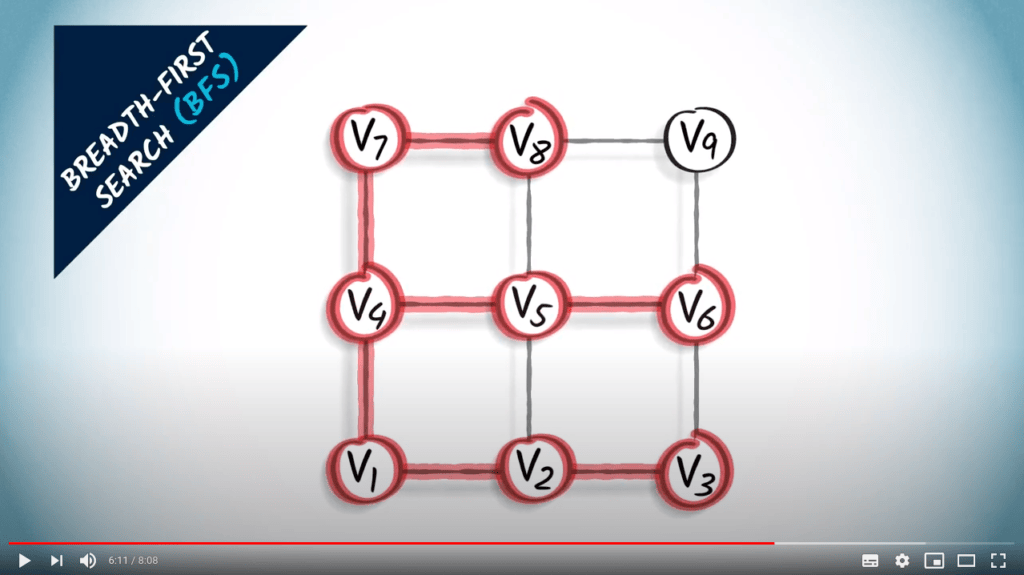
Graph traversal
Two strategies on a non-weighted graph

Graph traversal
Two strategies on a non-weighted graph

Graph traversal
Two strategies on a non-weighted graph

Graph traversal
Two strategies on a non-weighted graph
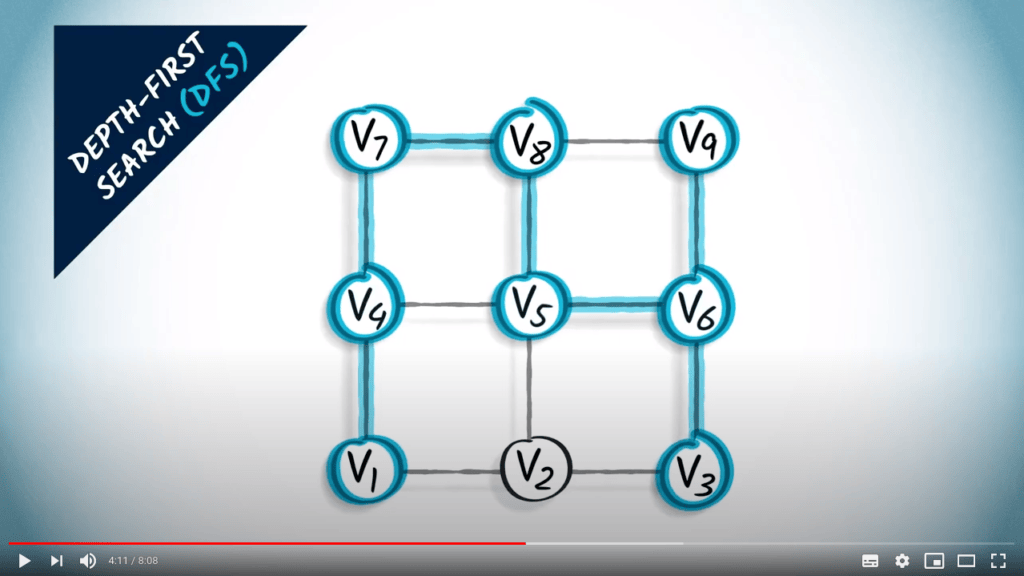

Graph traversal
Two strategies on a non-weighted graph
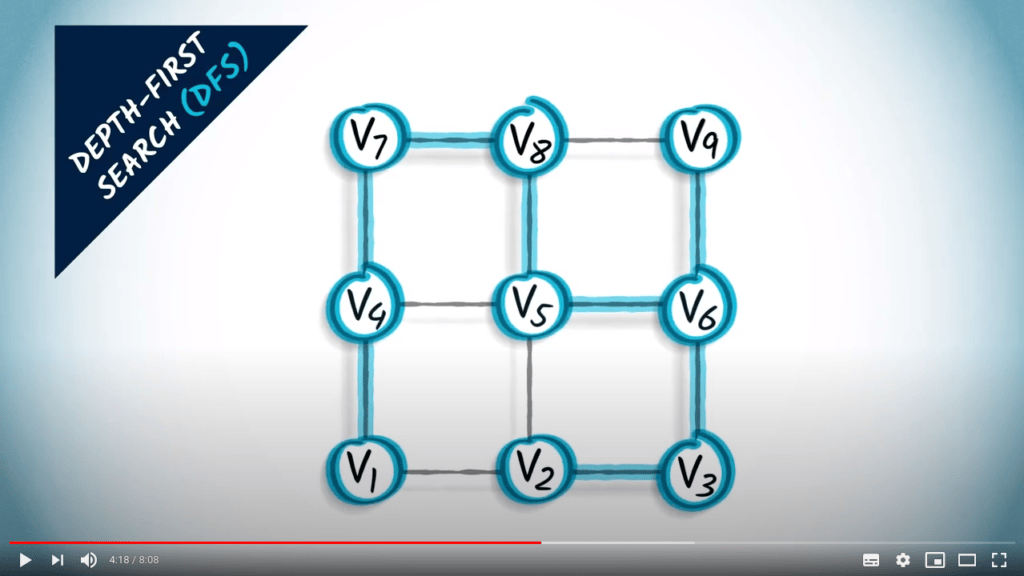

Graph traversal
Two strategies on a non-weighted graph
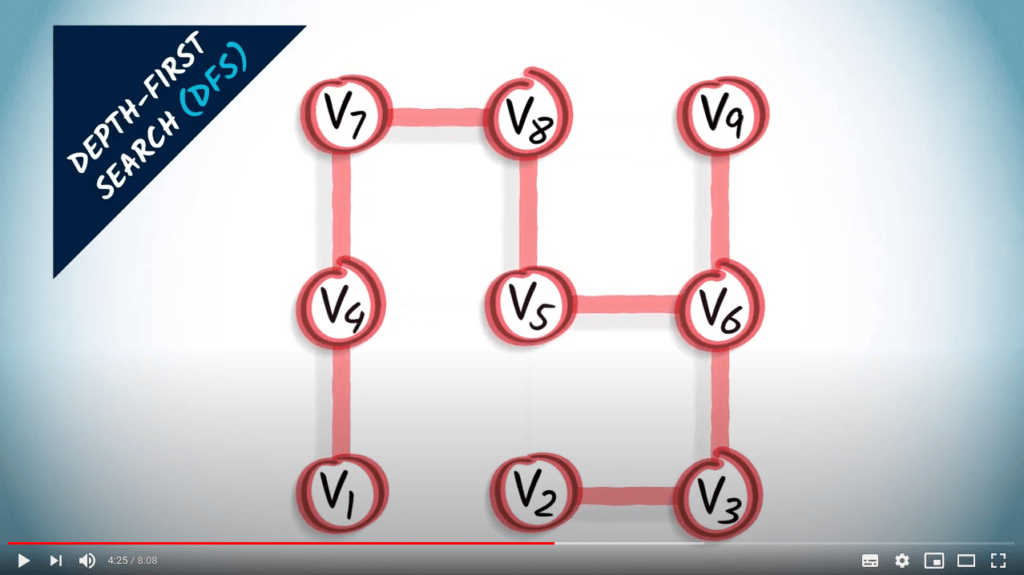
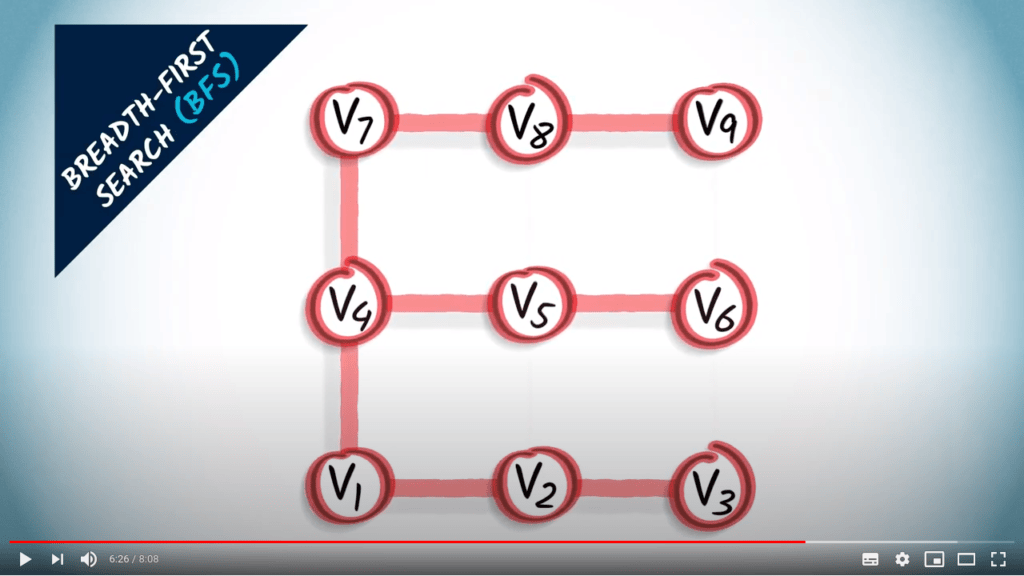
- A traversal coresponds to a spanning tree of the graph
- BFS finds the shortest path from $v_1$ to all other vertices
Routing tables
A way to store the spanning tree in memory
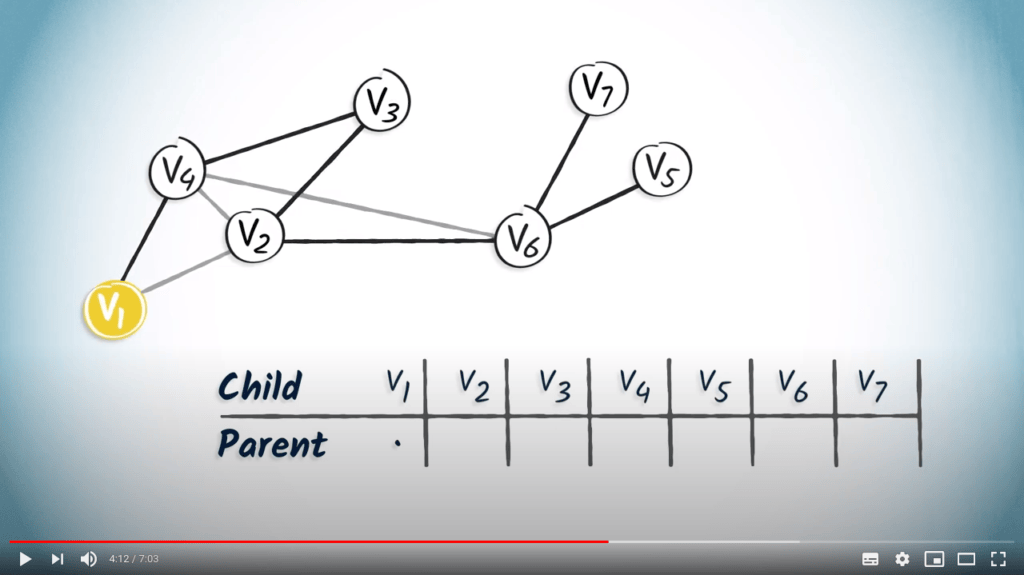
Routing tables
A way to store the spanning tree in memory
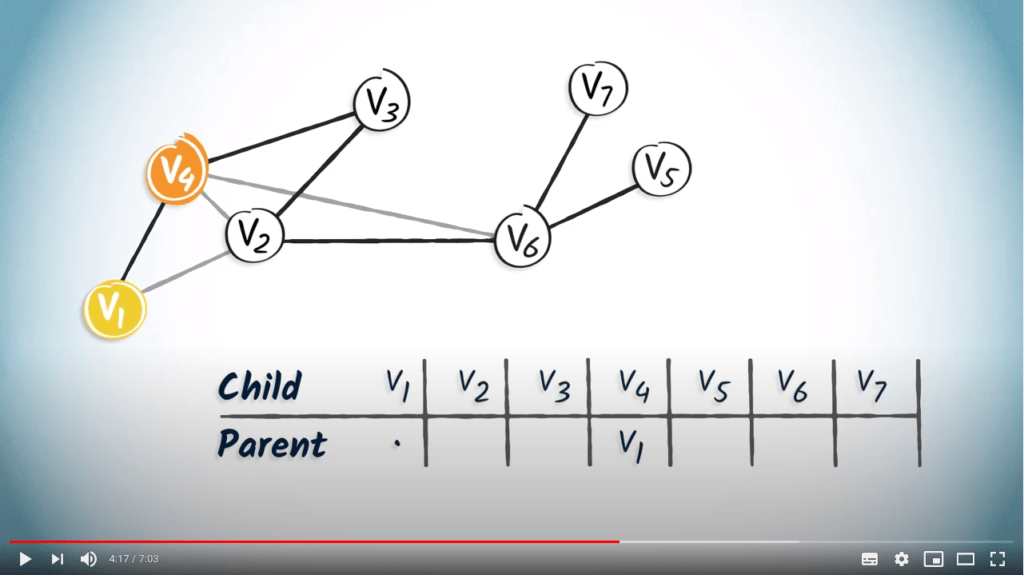
Routing tables
A way to store the spanning tree in memory
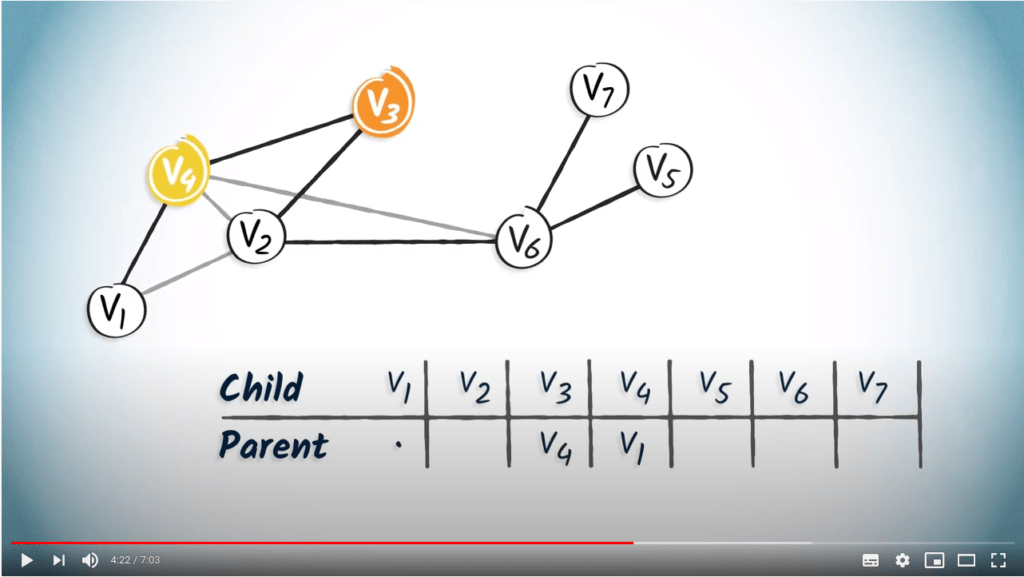
Routing tables
A way to store the spanning tree in memory
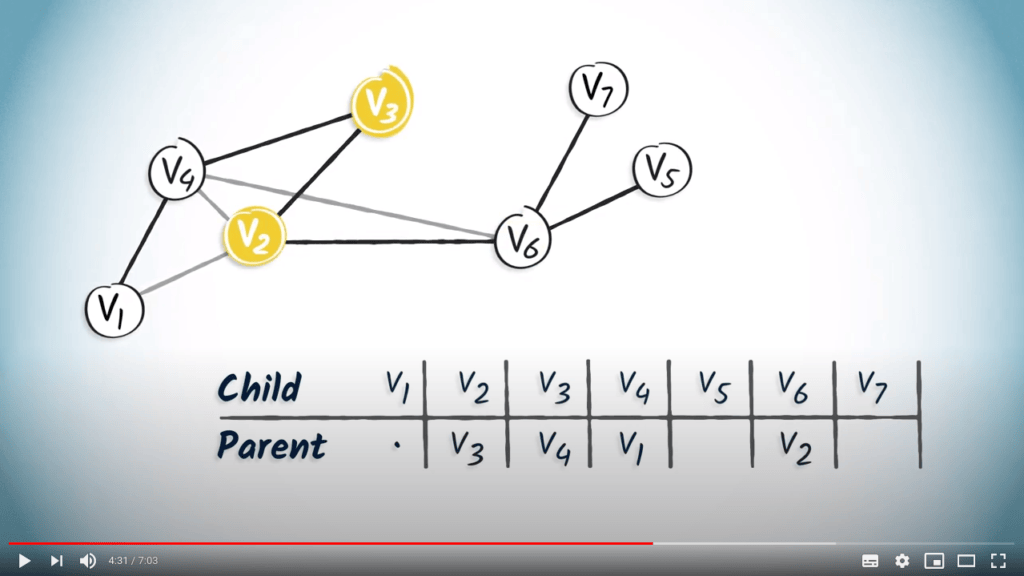
Routing tables
A way to store the spanning tree in memory
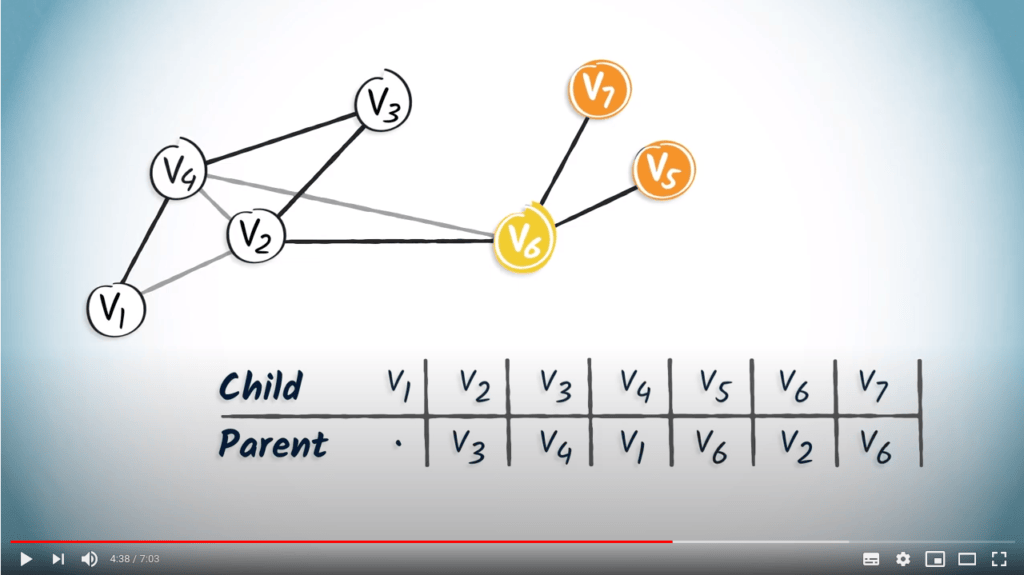
Routing tables
Retrieving the shortest path
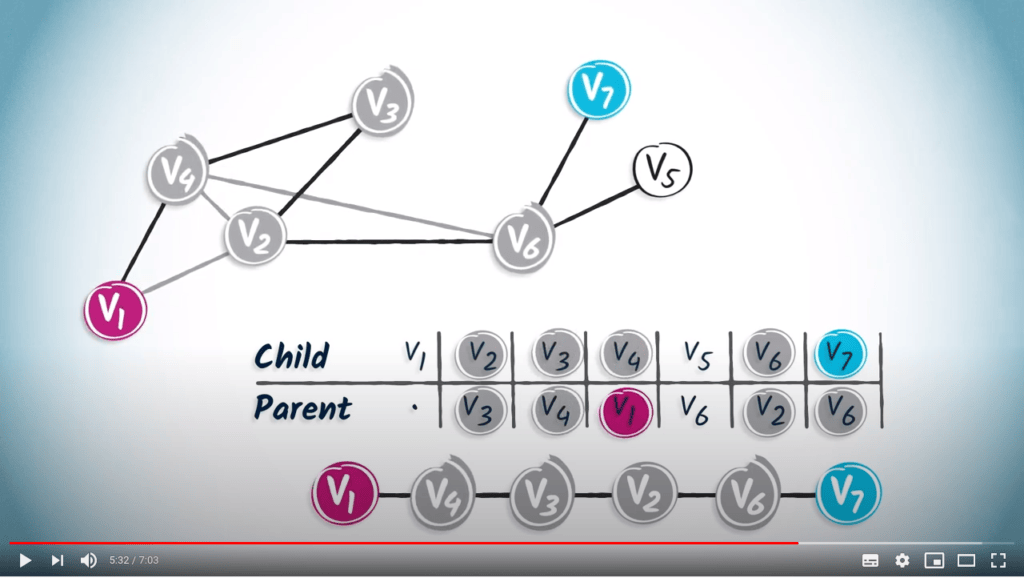
Queuing structures for graph traversals
Queues / First-In First-Out / FIFO

- Elements enter and exit the structure in the same order
- Adapted to a BFS
Queuing structures for graph traversals
Stacks / Last-In First-Out / LIFO

- First elements to enter the structure are the last ones to exit it
- Adapted to a DFS
Queuing structures for graph traversals
A unified algorithm
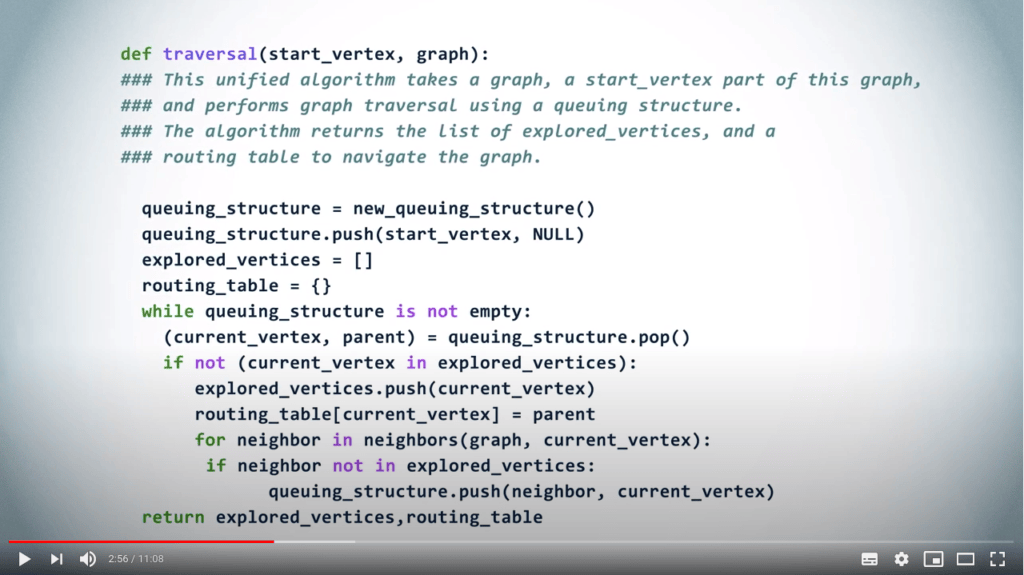
- The traversal performed depends on the order in which neighbors are explored
- The data structure used determines that order
Recap of the session
Main elements to remember
-
To address a problem: formalize, specify, then code
-
Graph theory provides an abstract modelization for elements of interest and their relationships
-
Traversals are algorithms made to explore a graph
-
BFS is a strategy that finds the shortest path in a non-weighted graph
-
Data structures have their properties, that can be exploited by algorithms
Recap of the session
What’s next?
Practical activity (~2h30)
Catch one cheese
- Program a DFS
- Program a BFS
- Compare algorithms
After the session
- Review the articles of the session
- Check your understanding with the quiz
- Complete the practical activity
- Check next session’s “Before the class” section
Evaluation
- Evaluated quiz to start next session!