Catch a single piece of cheese… with mud

Project – Session 3

• Dijkstra’s algorithm
• Min-heaps
• Recap of the session

Dijkstra’s algorithm

Finding the shortest path in a weighted graph

Dijkstra’s algorithm

A direct application of the BFS algorithm

Dijkstra’s algorithm

The actual shortest path

Dijkstra’s algorithm

How does it work?

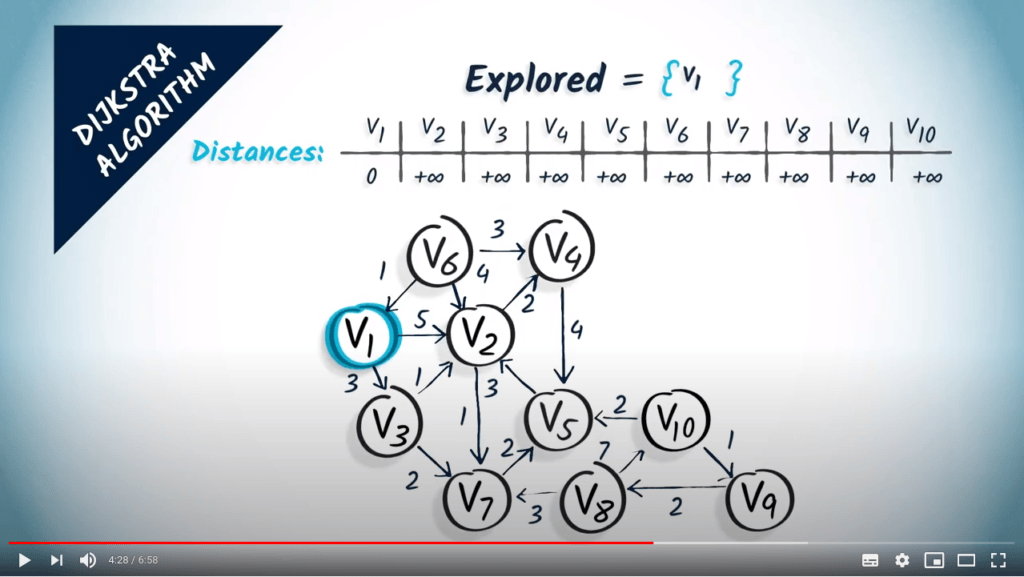
• Initialize an array of $+\infty$ distances to the initial vertex $v_1$
• Initialize a set to remember which vertices were explored

Dijkstra’s algorithm

How does it work?

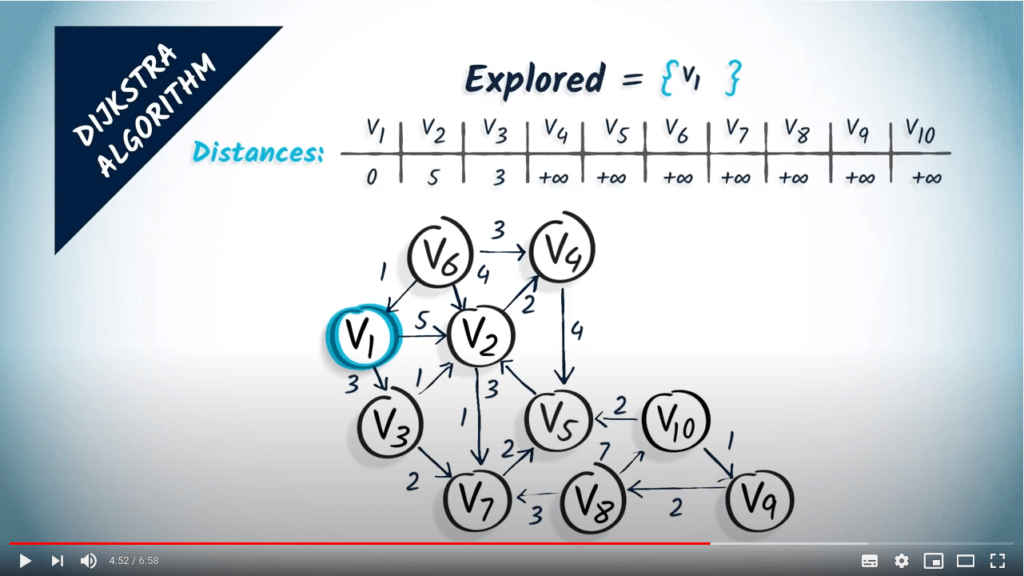
• Update the distances to accessible neighbors
• We update $v_2$ (distance of $5 < +\infty$) and $v_3$ (distance of $3 < +\infty$)

Dijkstra’s algorithm

How does it work?

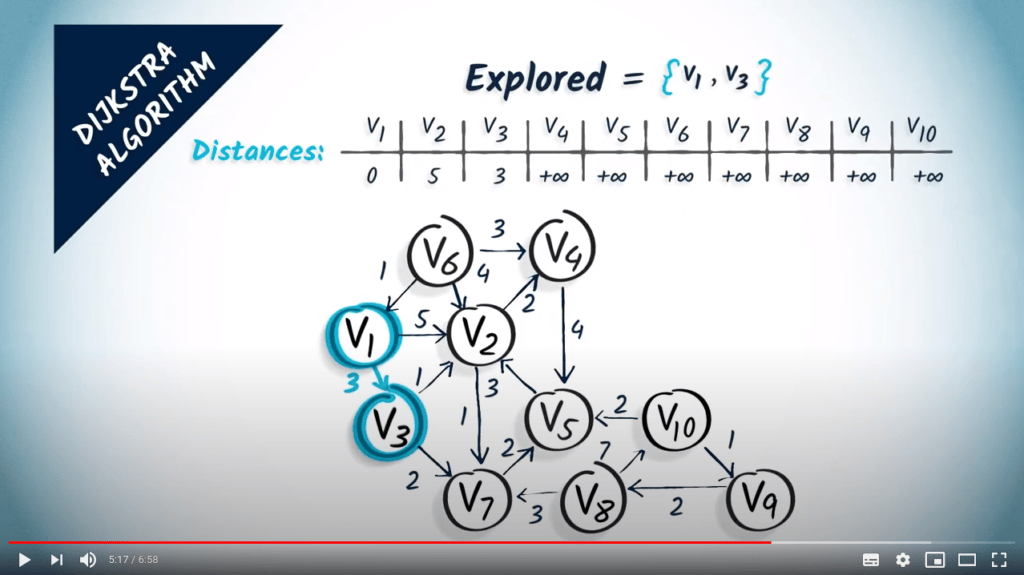
• Explore the unvisited neighbor with minimum distance to $v_1$
• We explore $v_3$

Dijkstra’s algorithm

How does it work?

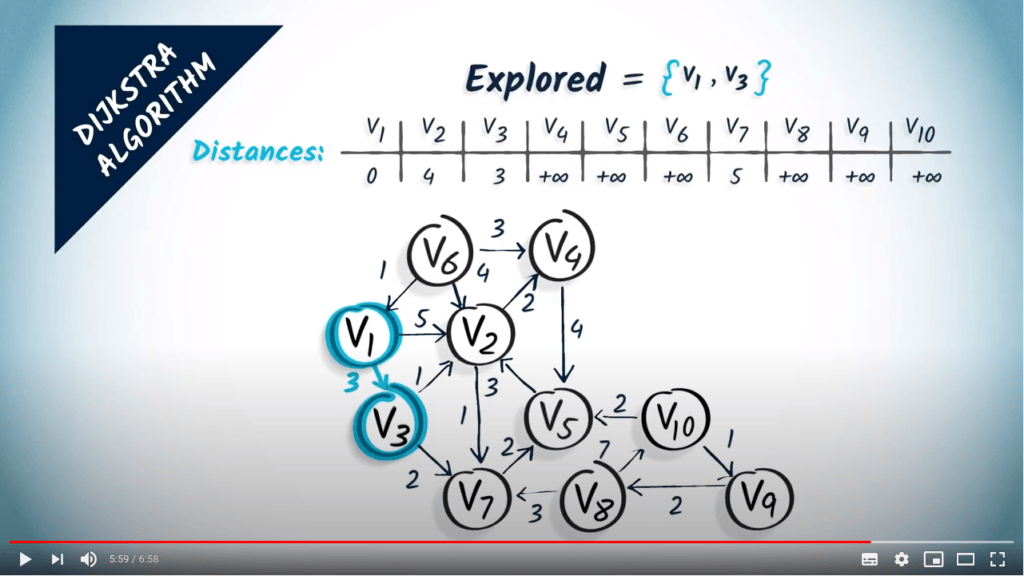
• Update the distances to accessible neighbors
• We update $v_2$ (distance of $3+1 < 5$) and $v_7$ (distance of $3+2 < +\infty$)

Dijkstra’s algorithm

How does it work?

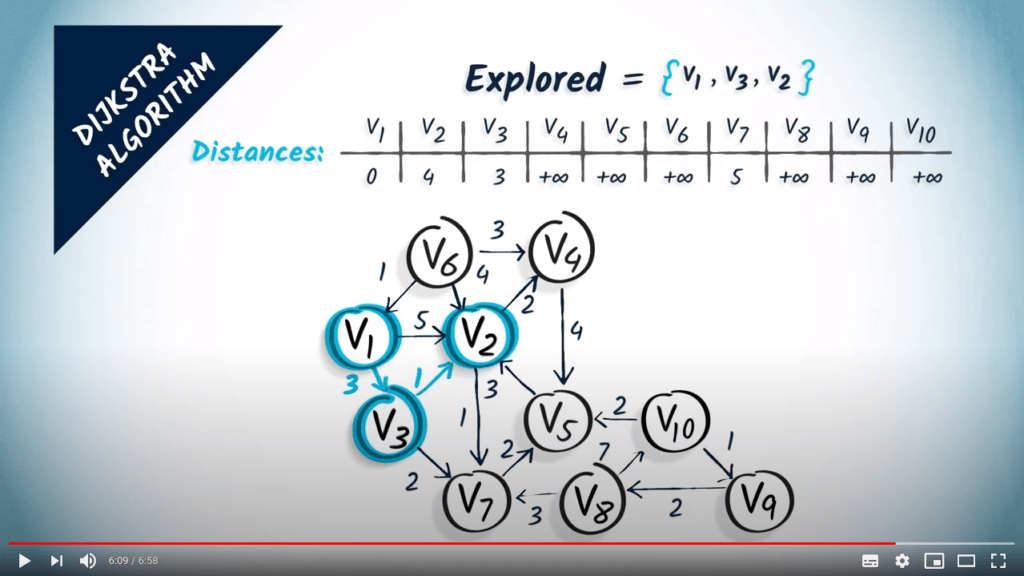
• Explore the unvisited neighbor with minimum distance to $v_1$
• We explore $v_2$

Dijkstra’s algorithm

How does it work?

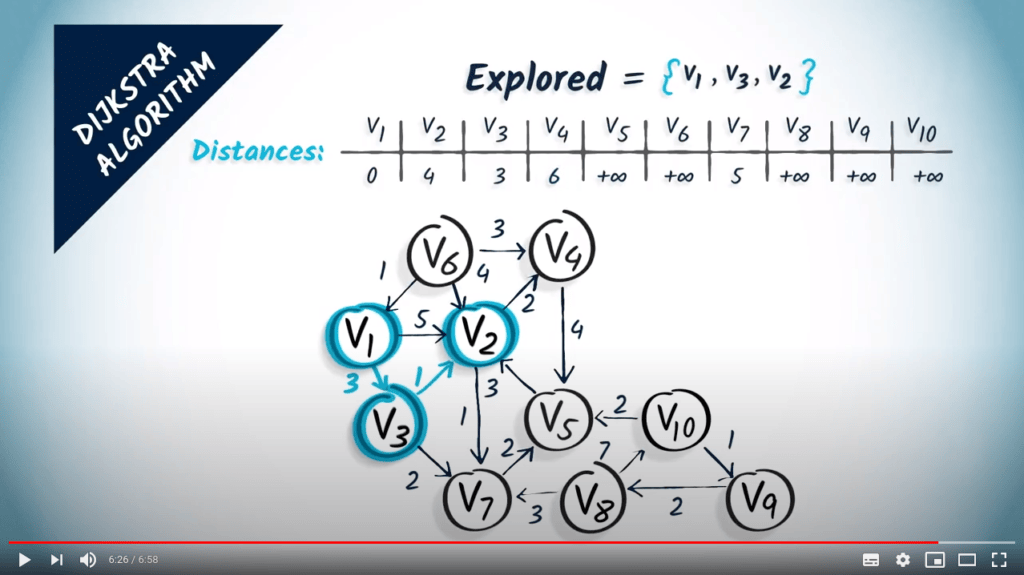
• Update the distances to accessible neighbors
• We update $v_4$ (distance of $3+1+2 < +\infty$)

Dijkstra’s algorithm

How does it work?

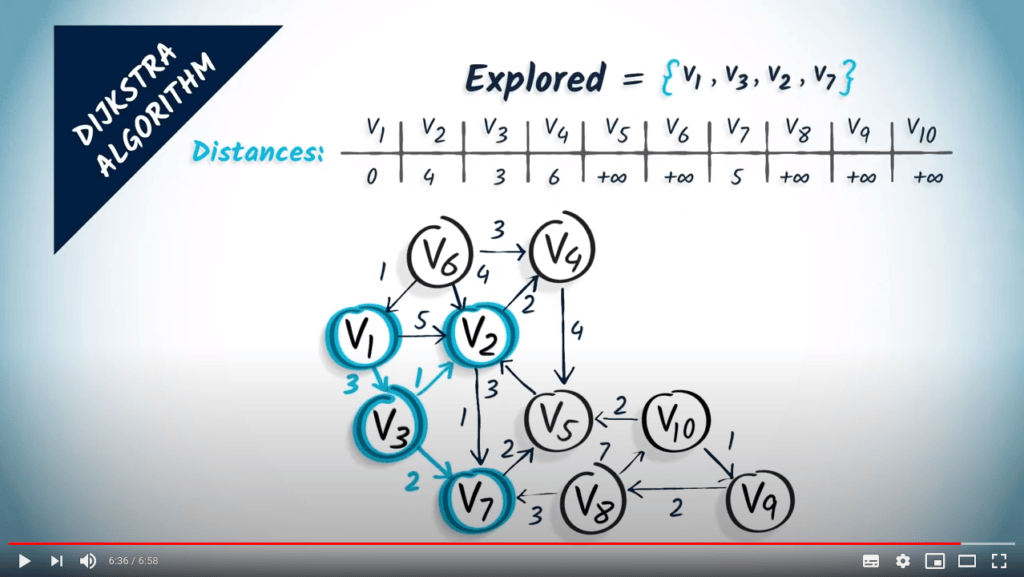
• Explore the unvisited neighbor with minimum distance to $v_1$
• We explore $v_7$, no distances to update

Dijkstra’s algorithm

How does it work?

• Explore the unvisited neighbor with minimum distance to $v_1$
• We explore $v_5$, no distances to update, we are done!

Min-heaps

Using a min-heap

# Create a min-heap
heap = new_heap()

[]

# Add elements to the heap
push(heap, ("A", 50))
push(heap, ("B", 22))
push(heap, ("C", 10))

[('A', 50), ('B', 22), ('C', 10)]

# Extract smallest element from the heap
pop(heap)

('A', 50)

Min-heaps

Dijkstra’s algorithm and min-heaps

• Explore the unvisited neighbor with minimum distance to $v_1$
• Maintain a min-heap with elements (distance to $v_1$, $v_x$)

Recap of the session

Main elements to remember

Recap of the session

What’s next?