Catch multiple pieces of cheese
Project – Session 4
- Algorithm complexity
- Problem complexity & NP-completeness
- The traveling salesman problem
- Bruteforce & backtracking to solve NP-complete problems
Algorithm complexity
How to compare algorithms efficiency?
Measure execution time
- Needs to run the program
- Dependent on hardware, programming language, other running processes…
Something more abstract: complexity
- Number of operations as a function of the input size $n$
- We use the $O(\cdot)$ notation, e.g., $O(n)$, $O(n^2)$, $O(n!)$
$\rightarrow$ Independent of hardware, programming language…
$\rightarrow$ Does not need the program to be run
- Examples – DFS/DFS: $O(|E|)$ ; Dijkstra: $O(|E| + |V| \cdot log(|V|))$
Algorithm complexity
Comparing algorithms using complexity
$$O(n) < O(n^2)$$
$$O(n) = O(123456789 \cdot n)$$
$$O(n^2) = O(n^2 + n)$$
$$O(n^{10000}) < O(n!)$$
$$O(n) = O(123456789 \cdot n)$$
$$O(n^2) = O(n^2 + n)$$
$$O(n^{10000}) < O(n!)$$
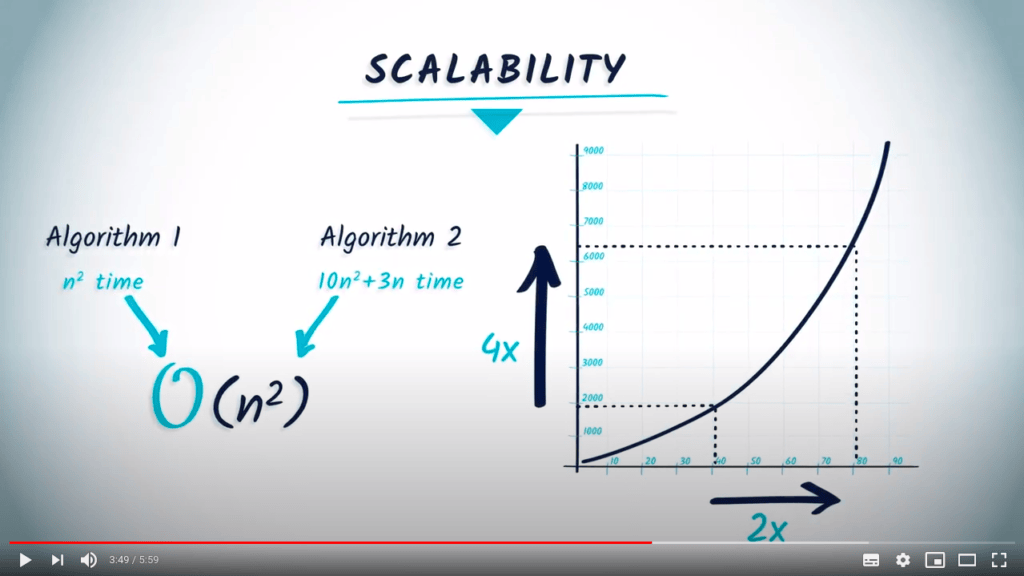
Remarks
- Compare asymptotic behavior
- We are interested in worst-case complexity, i.e., estimation in the least favorable case
Problem complexity & NP-completeness
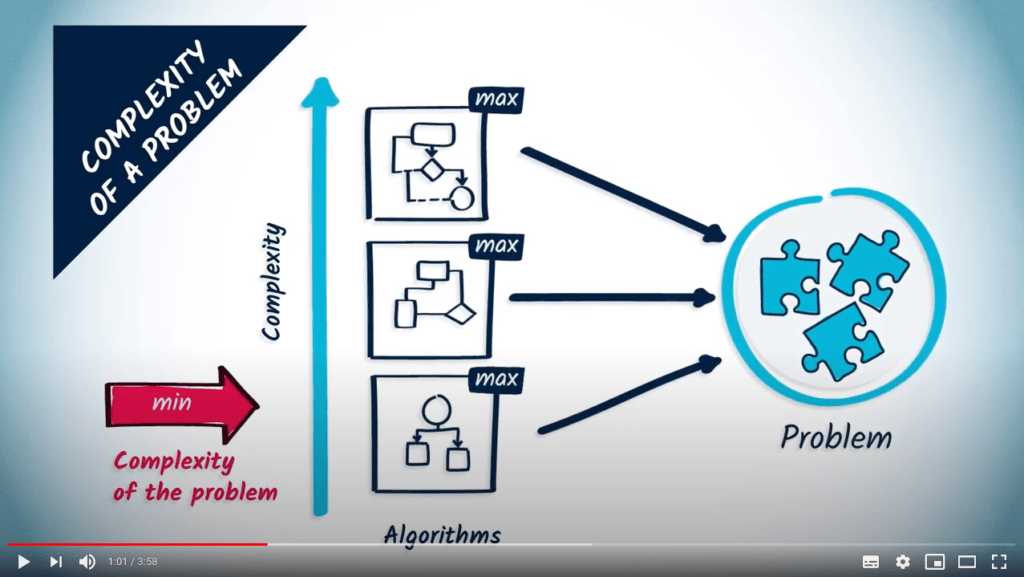
From algorithm complexity to problem complexity
The complexity of a problem is the minimum complexity of the algorithms solving the problem
Problem complexity & NP-completeness
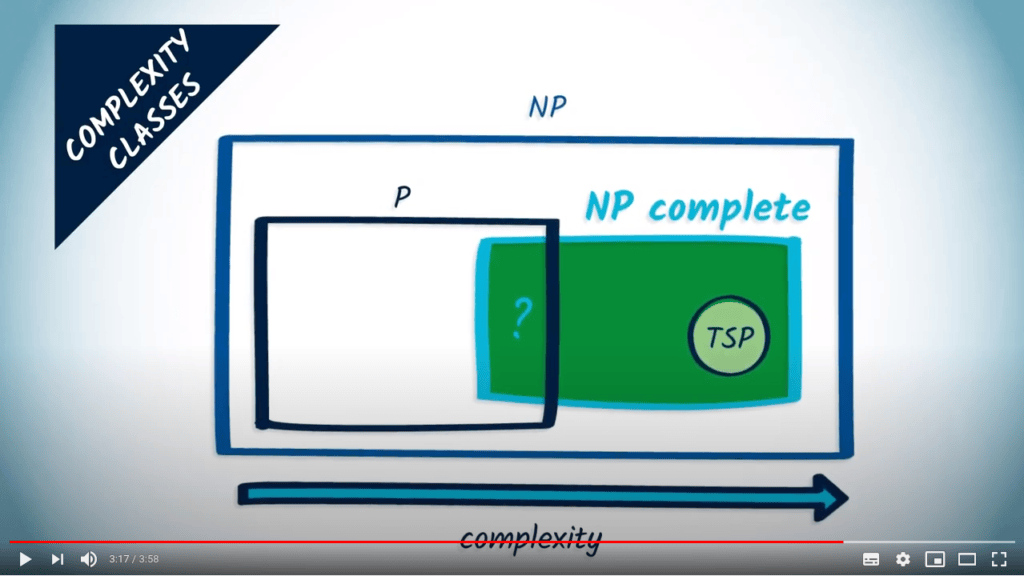
Complexity classes
- Equivalence classes between algorithms and problems
- Dijkstra, BFS, DFS are polynomial algorithms for finding paths (problems of class P)
- Some problems cannot be solved with a known polynomial algorithm, e.g, the traveling salesman problem (NP-complete problem)
The traveling salesman problem
Problem description
Find the shortest path that goes through all locations
The traveling salesman problem
Step 1: abstract useless details
Find the shortest route that goes through all vertices of a complete graph
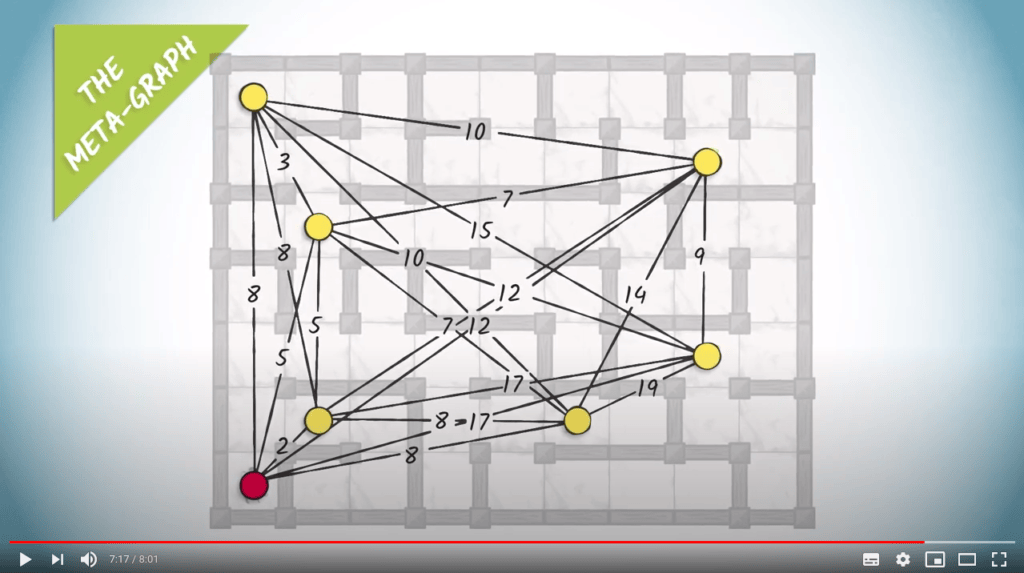
Bruteforce & backtracking to solve NP-complete problems
Step 2: test every permutation
- Note – This boils down to performing a DFS per branch
Bruteforce & backtracking to solve NP-complete problems
Step 2 (alternative): test (nearly) every permutation
- Number of skipped branches depend on quality of the first explored ones
- This doesn’t change the (worst-case) complexity
Recap of the session
Main elements to remember
-
Algorithms can be compared according to their complexity
-
Problem complexity is determined by the best algorithm to solve it
-
There are some very hard to solve problems, like TSP
-
Such problems can only be solved by testing all possible solutions
Recap of the session
What’s next?
Practical activity (~2h30)
Catch multiple pieces of cheese
- Program the TSP (+ backtracking)
- Use Dijkstra or BFS as a basis
After the session
- Review the articles of the session
- Check your understanding with the quiz
- Complete the practical activity
- Check next session’s “Before the class” section
Evaluation
- Evaluated quiz to start next session!