Algorithmic complexity
Reading time15 minEn bref
Résumé de l’article
La complexité algorithmique est une notion fondamentale en informatique. Elle permet de caractériser un algorithme et de fournir une estimation du temps nécessaire à son exécution, en fonction de ses entrées. Cela permet d’évaluer si un problème peut être résolu dans un temps raisonnable, mais aussi de comparer plusieurs algorithmes qui résolvent un même problème. De plus, c’est une mesure qui ne dépend pas de la qualité de votre processeur, car elle ne nécessite pas l’exécution du programme.
Points clés
-
La complexité algorithmique estime le temps nécessaire à l’exécution d’un algorithme.
-
La complexité s’exprime en fonction de la taille de l’entrée.
-
Il existe des classes de complexité.
-
On s’intéresse généralement à la complexité dans le pire des cas, mais d’autres mesures existent.
Contenu de l’article
1 — Complexité algorithmique
Le but de tout algorithme est de proposer une solution à un problème donné. Minimiser le temps de traitement est directement lié au nombre de calculs effectués.
La complexité algorithmique est une mesure de la performance d’un programme en termes de nombre de calculs qu’il réalise. Plus la complexité algorithmique est faible, moins l’algorithme effectue de calculs, et meilleure est sa performance.
Les boucles sont la principale cause du grand nombre de calculs. Une utilisation non contrôlée conduit à un nombre croissant d’opérations. Au-delà d’un certain nombre, le temps de calcul devient un obstacle à l’utilisation du programme. Il est donc important de pouvoir évaluer la performance d’un algorithme avant de le programmer.
2 — Analyse de la complexité
Il existe plusieurs méthodes d’analyse de la complexité, notamment :
- L’analyse moyenne fournit des informations sur le temps moyen de calcul.
- L’analyse pessimiste (pire cas) est la plus couramment utilisée. Elle fournit des informations sur le nombre de calculs à considérer dans un scénario de pire cas. Son objectif principal est d’évaluer les algorithmes dans leurs cas les plus extrêmes.
Par exemple, si un algorithme cherche un élément parmi $N$ données initiales, dans le pire des cas il devra parcourir toutes les données. L’analyse pessimiste indiquera que la recherche peut effectuer jusqu’à $N$ comparaisons. La complexité algorithmique est alors notée $O(N)$. La notation $O(\cdot)$ indique que l’analyse de performance se concentre sur la borne supérieure. La valeur $N$ indique qu’un maximum de $N$ opérations de traitement doivent être effectuées lorsqu’il y a $N$ données initiales.
3 — Principales catégories de complexité
La complexité varie d’un algorithme à l’autre, mais peut être regroupée dans les catégories suivantes :
3.1 — Algorithmes logarithmiques
Ils sont notés $O(log(N))$. Ces algorithmes sont très efficaces en termes de temps de traitement. Le nombre de calculs dépend du logarithme du nombre initial de données à traiter. La fonction $log(N)$ a une courbe qui s’aplatit horizontalement à mesure que le nombre de données augmente. Le nombre de calculs augmente légèrement avec la quantité de données à traiter (voir figure ci-dessous).
La fonction logarithme donne un résultat différent selon la base sur laquelle elle est calculée, ex. $log_{10}(1000) = 3$, $log_2(1000)= 9.97$ ou $ln(1000)=6.9$.
Les algorithmes logarithmiques traitent l’ensemble de données en le divisant en deux parties égales, puis répètent le processus sur chaque moitié. C’est le logarithme en base 2, $log_2(N)$. Pour simplifier l’écriture de la complexité de ces algorithmes, la notation $log(N)$ est utilisée au lieu de $log_2(N)$.
La recherche dichotomique est l’un de ces algorithmes. Vous cherchez dans la moitié où se trouve la donnée, puis répétez la recherche en divisant la moitié sélectionnée par deux. Cependant, les données doivent être triées au préalable, ce qui fait $log_2(N)$ comparaisons.
3.2 — Algorithmes linéaires
Ils sont notés sous la forme $O(N)$. Ce sont des algorithmes rapides. Le nombre de calculs dépend linéairement du nombre de données initiales à traiter.
Considérons un algorithme qui cherche un nom dans une liste de 1 000 noms et compare ce nom avec chacun des noms de la liste. Si le traitement de 1 000 données initiales ($N$) nécessite 1 000 calculs de base pour trouver le résultat, la complexité de l’algorithme est $O(N)$. Si un autre algorithme, avec la même quantité de données initiales, effectue 2 000 opérations pour obtenir le résultat, sa complexité est $O(2N)$.
Cependant, avec la complexité, on s’intéresse généralement à l’ordre des calculs. Pour cette raison, on néglige généralement les constantes, donc on dira souvent que les deux algorithmes ont une complexité $O(N)$.
3.3 — Algorithmes linéaires et logarithmiques
Ils sont notés sous la forme $O(N \cdot log(N))$. Ce sont des algorithmes qui divisent à plusieurs reprises un ensemble en deux parties et itèrent complètement sur chaque partie.
Considérons un algorithme qui cherche la plus longue sous-séquence croissante. Le but est de trouver une sous-séquence d’une séquence donnée dans laquelle les éléments de la sous-séquence sont triés par ordre croissant et dans laquelle la sous-séquence est la plus longue possible. Cette sous-séquence n’est pas nécessairement contiguë ni unique.
3.4 — Algorithmes polynomiaux
Ils sont notés sous la forme $O(N^p)$, où $p$ est la puissance.
Un algorithme qui compare une liste de 1 000 noms avec une autre liste de 1 000 noms, et itère sur la seconde liste pour chaque nom de la première, effectue $1,000 \times 1,000$ calculs. Il est de type $O(N^2)$. Les algorithmes dont la complexité est au carré sont aussi appelés quadratiques.
3.5 — Algorithmes exponentiels ou factoriels
Ils sont notés sous la forme $O(e^N)$ ou $O(N!)$. Ce sont parmi les algorithmes les plus complexes. Le nombre de calculs augmente de façon exponentielle ou factorielle selon les données traitées.
Un algorithme exponentiel traitant 10 données initiales effectuera 22 026 calculs, tandis qu’un algorithme factoriel en effectuera 3 628 800. Ce type d’algorithme se rencontre couramment dans les problèmes d’intelligence artificielle (IA).
4 — Résumé
Visuellement, on peut comprendre les relations entre les complexités comme suit :
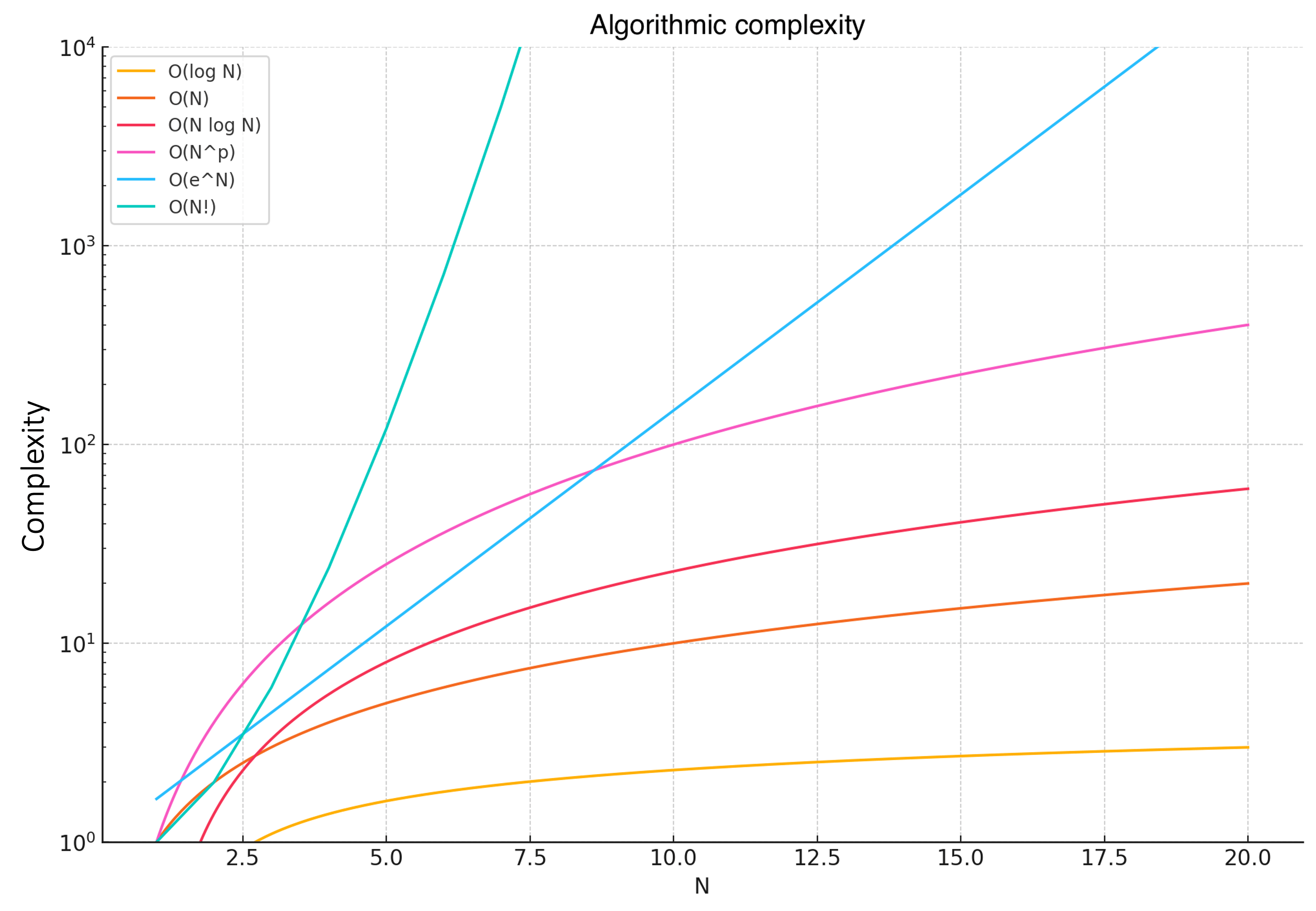
Les courbes montrent clairement comment chaque fonction de complexité croît avec l’augmentation de $N$.
- $O(log(N))$ – Croissance très lente de la courbe (complexité faible).
- $O(N)$ – Croissance linéaire de la courbe.
- $O(N \cdot log(N))$ – Croissance légèrement plus rapide de la courbe.
- $O(N^2)$ – Croissance quadratique.
- $O(e^N)$ – Croissance exponentielle (complexité très élevée).
- $O(N!)$ – Croissance factorielle (complexité extrêmement élevée).
Bien que la gestion de la mémoire ne soit pas incluse dans la notion de complexité, elle en dépend souvent. Il est courant d’utiliser plus de mémoire pour minimiser le nombre d’opérations. Il faut donc vérifier que la gestion mémoire des algorithmes performants ne devienne pas une nouvelle contrainte à leur utilisation.
Pour aller plus loin
5 — Complexité minimale
Parfois, on s’intéresse aussi à déterminer le temps minimal qu’un algorithme doit prendre pour résoudre un problème. Lorsque $N$ devient suffisamment grand, si le temps d’exécution d’un algorithme est au moins $kf(N)$ pour une certaine constante $k$ et une fonction $f(N)$ de $N$ (par exemple, $N!$ ou $N^2$), on décrit le temps d’exécution comme $\Omega(f(N))$.
Enfin, si le temps d’exécution d’un algorithme est à la fois $O(f(N))$ et $\Omega(f(N))$, on dit que le temps d’exécution est $\Theta(f(N))$. Cela signifie que, à une constante près, lorsque $N$ devient suffisamment grand, le temps d’exécution est borné entre $k_1f(N)$ et $k_2f(N)$ pour certaines constantes $k_1$ et $k_2$.
Pour aller au-delà
- TimeComplexity.
The complexities of various methods of standard data structures in Python.