Binary search tree

En bref

Résumé de l’article

Nous présentons la structure de données appelée “arbre binaire de recherche” (BST). Cette structure de données permet de maintenir un ensemble ordonné, supportant des opérations efficaces telles que l’insertion et la recherche des valeurs minimales.

Les opérations clés dans un BST, telles que la recherche de la valeur minimale et l’insertion d’une nouvelle clé tout en préservant la structure de l’arbre, sont expliquées avec des algorithmes et du pseudocode.

Points clés à retenir

• Un BST maintient l’ordre en plaçant les valeurs plus petites à gauche et les valeurs plus grandes à droite de chaque nœud.

• Les opérations comme la recherche du minimum ou du maximum sont efficaces car la structure de l’arbre réduit le nombre de comparaisons.

• L’insertion dans un BST et la recherche de la valeur minimale ont toutes deux une complexité temporelle de $O(h)$, où $h$ est la hauteur de l’arbre.

• Les BST sont efficaces lorsqu’ils sont équilibrés, c’est-à-dire $h= O(log_2(n))$, bien que leurs performances puissent se dégrader si l’arbre est déséquilibré.

Contenu de l’article

1 — Choisir une structure de données

Dans le cours précédent, vous avez exploré différentes façons de stocker des données, telles que les tableaux et les listes chaînées. Selon la manière dont vous comptez utiliser les données, certaines opérations peuvent être effectuées plus efficacement avec des structures de données spécifiques. Il est donc important de choisir une structure de données qui convient le mieux aux exigences de votre problème. Dans ce cours, nous allons nous concentrer sur les arbres binaires de recherche, un type de structure de données qui permet une insertion efficace de nouvelles données tout en conservant la capacité à trouver rapidement les valeurs minimales dans l’ensemble de données.

Mais pourquoi ce problème est-il important ? Une application simple est la suivante :

Vous êtes responsable de la planification des tâches d’apprentissage automatique (ML) pour un cluster de calcul haute performance. Différentes tâches ont des niveaux d’urgence variables basés sur des facteurs tels que les délais, les besoins en calcul et l’impact des résultats. Par exemple, une tâche qui affine un modèle pour une application médicale urgente devrait probablement obtenir des ressources de calcul plus rapidement qu’une tâche par lots entraînant un modèle pour des recommandations de films, indépendamment du temps de soumission.

Comment choisir toujours la tâche ML la plus urgente lorsque de nouvelles tâches continuent d’arriver ?

Du point de vue d’un informaticien, votre problème est le suivant :

Quelle structure de données devez-vous choisir pour ajouter facilement de nouvelles tâches et retirer rapidement la tâche la plus urgente ?

Nous pourrions commencer avec une liste de taille $N$. Mais quel type de liste ?

1. Option 1 – Stocker les tâches dans une liste :

   • Ajouter une nouvelle tâche est d’ordre $O(N)$. En effet, rappelez-vous qu’un tableau est excellent pour les opérations statiques, mais pas du tout pour les opérations dynamiques. Par exemple, lors de l’ajout ou de la suppression d’un élément (et non du remplacement d’un élément à un certain emplacement), vous êtes obligé de réallouer le tableau et de décaler tous les éléments après l’élément modifié.
   • Supprimer le min/max se fait en recherchant dans toute la liste et sera donc d’ordre $O(N)$.

2. Option 2 – Stocker les tâches dans une liste triée :

   • Ajouter une nouvelle tâche est d’ordre $O(N)$.
   • Supprimer une tâche est d’ordre $O(1)$.

Nous cherchons une structure de données où ces opérations sont en $\Theta(log(N))$. Une structure possible qui satisfait ces propriétés s’appelle un arbre binaire de recherche.

2 — Arbre binaire de recherche (BST)

2.1 — Définition d’un BST

Commençons par donner la définition d’un arbre binaire :

Un arbre binaire est un arbre (un graphe connexe sans cycles) où chaque nœud possède les champs suivants :

• Un élément avec un champ clé.
• Une référence à un nœud parent (qui peut être absent).
• Une référence à un nœud enfant gauche (qui peut être absent).
• Une référence à un nœud enfant droit (qui peut être absent).

Utilisons les notations suivantes dans le reste de cet article :

• x – Le nœud courant dans l’arbre.
• x.key – La clé associée au nœud x.
• x.left – L’enfant gauche du nœud x.
• x.right – L’enfant droit du nœud x.
• NIL : une valeur nulle ou un indicateur de nœud feuille, signifiant qu’il n’y a pas d’enfant.

Pour mieux comprendre comment fonctionne un arbre binaire, vous pouvez jeter un œil à la bibliothèque binarytree (voir la documentation). Voici un exemple de code pour visualiser différents arbres :

# Needed imports
from binarytree import tree, bst, heap, build

# Create a tree using functions from library binarytree
my_tree = tree(height=3, is_perfect=False)
print(my_tree)

# Build the tree from some values
values = [1, 14, 10, 5, 7]
my_tree = build(values)
print(my_tree)

2.2 — La propriété BST

On dit qu’un arbre binaire satisfait la propriété d’arbre binaire de recherche si pour chaque nœud :

• Les clés dans le sous-arbre gauche d’un nœud sont inférieures à la clé stockée dans le nœud.
• Les clés dans le sous-arbre droit du nœud sont supérieures à la clé stockée dans le nœud.

Exemples d’arbres binaires avec ou sans la propriété d’arbre binaire de recherche :

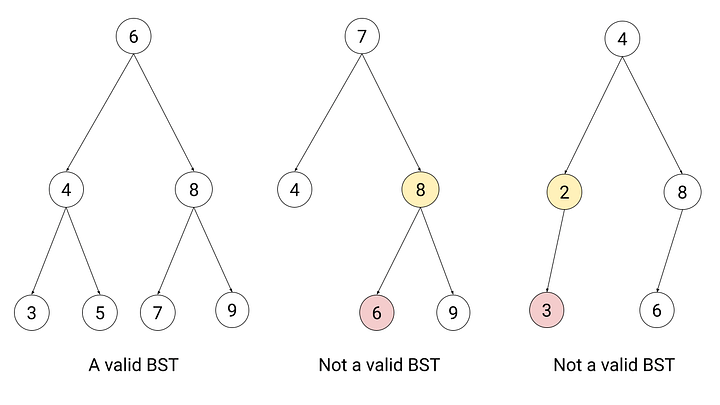
Pour plus d’informations, visitez la source de l’image.

2.3 — Opérations sur un BST

Revenons à notre problème, nous allons définir des algorithmes pour trouver efficacement le minimum ou le maximum et insérer ou supprimer rapidement des éléments dans un arbre binaire de recherche.

2.3.1 — Minimum

Une façon efficace de trouver le nœud associé à la clé minimale dans un BST est simplement de suivre l’enfant gauche depuis la racine jusqu’à rencontrer une valeur NIL. Le pseudocode est donné ci-dessous :

TREE-MINIMUM(x)
    while x.left ≠ NIL
        do x = x.left
    return x

Observez que si la propriété d’arbre binaire de recherche est satisfaite, alors TREE-MINIMUM(x) est correct (ce qui signifie que le minimum est trouvé).

La complexité de TREE-MINIMUM(x) est d’ordre $O(h)$, où $h$ est la hauteur de l’arbre.

Vous pouvez maintenant réfléchir à la façon de concevoir TREE-MAXIMUM(x) qui devrait retourner le nœud associé à la clé maximale dans un BST.

2.3.2 — Insertion dans un BST

Lorsque nous voulons insérer une clé dans un BST, une des principales difficultés est de maintenir la propriété d’arbre binaire de recherche. L’approche classique est d’insérer la nouvelle clé à une feuille. Pour décider après quelle feuille la nouvelle clé doit être ajoutée, la procédure itérative suivante peut être suivie :

• Si la nouvelle clé est inférieure au nœud courant, on se déplace dans le sous-arbre gauche.
• Sinon, on se déplace dans le sous-arbre droit.

Pour implémenter effectivement l’insertion dans un BST, vous pouvez utiliser la récursion (vous verrez des implémentations dans le pratique) ou pour chaque nœud x, vous devrez aussi définir son parent x.p (le pseudocode ci-dessous utilise cette méthode).

Vous pouvez trouver le pseudocode ci-dessous :

TREE-INSERT(T, z)
    x = T.root 
    y = NIL 
    while x ≠ NIL 
        y = x
        if z.key < x.key
            x = x.left
        else
            x = x.right
    z.p = y 
    if y == NIL
        T.root = z // tree T was empty
    elseif z.key < y.key
        y.left = z
    else
        y.right = z

Dans ce pseudocode, la variable x suit le chemin dans l’arbre et y est le parent courant de x. La boucle while aux lignes 3–8 fait descendre les deux variables dans l’arbre, allant à gauche ou à droite selon que la clé de z est plus grande ou plus petite que la clé du nœud courant x. Si x est NIL, alors une feuille a été atteinte. Cette feuille est l’endroit où l’élément ``_ est placé. Les lignes 9–15 définissent les variables pour s’assurer que z est inséré au bon endroit dans l’arbre.

TREE-INSERT(T, z) s’exécute en $O(h)$, où $h$ est la hauteur de l’arbre.

Pour aller plus loin

Nous avons dit précédemment que la plupart des complexités des différentes opérations effectuées sur un arbre dépendent de sa hauteur. Il est donc important que, lorsque nous ajoutons un élément, même si nous voulons conserver la propriété d’arbre binaire de recherche, la hauteur ne croisse pas linéairement avec le nombre de nœuds.

Vous pouvez essayer de voir à quoi ressemble l’arbre lorsque vous faites TREE-INSERT(T, z) sur la liste [1, 2, 3, 4, 5] et [3, 4, 1, 2, 5]. Vous observerez que l’ordre dans lequel vous traitez la liste change complètement la hauteur de l’arbre.

En pratique, nous sommes intéressés par un arbre ayant une hauteur $O(log_2(n))$. En effet, $log_2(n)$ est la borne inférieure optimale sur la hauteur d’un arbre avec $n$ nœuds. Ces arbres sont appelés arbres équilibrés.

Les arbres équilibrés doivent avoir les propriétés suivantes :

• Pour chaque nœud, la différence absolue entre les hauteurs des sous-arbres gauche et droit doit être inférieure à 1.
• Pour chaque nœud, le sous-arbre gauche (resp. droit) doit être un arbre binaire équilibré.

Une solution simple pour s’assurer que l’arbre reste équilibré une fois qu’on ajoute un élément est de “faire pivoter” l’arbre pour diminuer la hauteur de l’arbre. Une rotation implique une paire de nœuds $x$ et son parent $y$. Si $x$ est initialement l’enfant gauche de $y$, alors après la rotation $y$ devient l’enfant droit de $x$.

Vous pouvez trouver un exemple dans l’image ci-dessous : Pour plus d’informations, visitez la source de l’image.

Vous pouvez trouver le pseudocode ci-dessous pour LEFT-ROTATE :

LEFT-ROTATE(T, x)
    y = x.right
    x.right = y.left 
    if y.left ≠ T.nil 
        y.left.p = x 
    y.p = x.p 
    if x.p == T.nil 
        T.root = y 
    elseif x == x.p.left 
        x.p.left = y 
    else
        x.p.right = y 
    y.left = x         
    x.p = y

Notez qu’une des belles propriétés de la rotation est que la propriété BST est toujours satisfaite après la rotation.

Vous pouvez maintenant implémenter les fonctions LEFT-ROTATE(T, x) et RIGHT-ROTATE(T, x) et essayer de voir comment faire pour que la hauteur de l’arbre ne soit pas trop grande ! En pratique, lorsque vous voulez toujours avoir un arbre équilibré, vous devez utiliser soigneusement LEFT-ROTATE(T, x) et RIGHT-ROTATE(T, x) lors de l’ajout ou de la suppression d’un élément. Différentes approches conduisent à différents arbres de recherche équilibrés tels que :

Les différents pseudocodes montrés dans cette partie du cours se trouvent dans les chapitres 12 et 13 du livre Introduction to Algorithms, Fourth Edition.

Pour aller plus loin

• Red-Black Trees.

  Une autre structure de données basée sur les arbres.

• AVL Trees.

  Un arbre équilibré avec des contraintes supplémentaires. ```