Practical session

Présentation & objectifs

Dans cette activité pratique, nous vous guidons à travers une première utilisation des outils d’apprentissage automatique. Nous nous appuierons sur des données sous forme de matrice, et implémenterons à la fois un algorithme $k$-NN et un algorithme $k$-means. Plus tard, dans la session de programmation 5, nous utiliserons des bibliothèques existantes pour plus d’efficacité.

Contenu de l’activité

1 — Préparation des données

L’objectif de ce premier exercice est de :

• Vous familiariser avec la manipulation de données multidimensionnelles.
• Générer un jeu de données synthétique composé de nuages de points.
• Diviser ce jeu de données en un ensemble d’entraînement et un ensemble de test.

Pour cela, nous utiliserons le package numpy en Python.

1.1 — Comment créer des tableaux

Numpy propose plusieurs fonctions pour construire des tableaux :

• Création de tableaux avec np.array(), np.zeros(), np.ones(), np.arange().
• Utilisez la fonction np.shape() sur n’importe quel tableau numpy pour connaître sa forme (nombre de lignes, colonnes, etc.).

La fonction np.array() convertit une liste Python (ou une liste de listes) en un tableau numpy. Vous pouvez également créer des tableaux remplis de zéros ou de uns en utilisant np.zeros() et np.ones().

Voici quelques exemples de définition de tableaux en Python avec numpy :

# Needed imports
import numpy as np



# Creating a 1D array from a list
array_1d = np.array([1, 2, 3, 4, 5])
print("1D Array:", array_1d)

# Creating a 2D array (list of lists)
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("2D Array:\n", array_2d)

# Creating a 1D array of zeros
zeros_1d = np.zeros(5)
print("1D Array of zeros:", zeros_1d)

# Creating a 2D array (3 rows, 4 columns) of zeros
zeros_2d = np.zeros((3, 4))
print("2D Array of zeros:\n", zeros_2d)

# Creating a 2D array (2 rows, 3 columns) of ones
ones_2d = np.ones((2, 3))
print("2D Array of ones:\n", ones_2d)
print(np.shape(ones_2d))

Une fois les tableaux numpy définis, vous pouvez accéder à leurs valeurs (ou groupes de valeurs), en utilisant des crochets, comme pour les listes, mais en séparant les dimensions avec des virgules (,). Vous pouvez aussi utiliser les deux-points (:) pour sélectionner tous les éléments d’une dimension, et utiliser des entiers négatifs pour compter à rebours.

Illustration avec quelques exemples d’indexation utiles :

# Once numpy arrays have been defined, you can access their values (or groups of values), using square brackets, like lists, but separating dimensions using `,`. 
print("Array1D: " , array_1d)
print("Array2D: " , array_2d)

# Accessing elements of a 1D array
print("Element of array1d at index 0:", array_1d[0])
print("Element at array1d at index 1:", array_1d[1])

# Accessing elements of a 2D array
print("Element of array2d at 0, 0:", array_2d[0, 0])
print("Element at array2d 0, 1:", array_2d[0, 1])

# Accessing all elements of a row
print("All elements of array2d row 0:", array_2d[0])
print("All elements of array2d, column 0: ", array_2d[:,0])

# Accessing the last row
print("Elements of last row:", array_2d[-1])
print("Element at last row, second column:", array_2d[-1, 1])
print("Elements of second to last column:", array_2d[:,-2])

# It is also possible to use an array of booleans (`True` or `False`, or ones and zeros) in order to select specific rows / columns

# Select elements that are greater than 2, and get their indices
print(f"Elements greater than 2: {array_1d[array_1d > 2]}, at indices {np.where(array_1d > 2)}")

# Use a vector of indices to select specific elements
print("Elements at 0, 2, 4 of array_1d:", array_1d[[0, 2, 4]])

Un tutoriel plus complet sur l’indexation est disponible ici : numpy tutorial on indexing.

Enfin, il est aussi possible de générer des tableaux aléatoires avec numpy, avec les fonctions np.random.normal(), np.random.uniform(), np.random.randint().

1.2 — Génération de données synthétiques

En utilisant ces fonctions, générez un jeu de données synthétique :

• cloudA et cloudB, deux nuages (ensembles) de points en dimension 2, suivant une distribution normale centrée autour de deux coordonnées distinctes (coord1_A ou coord1_B) avec une variance 1 (coord2_A ou coord2_B).
• Le nombre de points à générer dans chaque nuage est donné, N_A = 500 et N_B = 200.

# Needed imports
import numpy as np



# Parameters of the first distribution
coord1_A, coord2_A = (1, 1)

# Number of points in the first cloud
N_A = 500

# Parameters of the second distribution
coord1_B, coord2_B = (-1, 1)

# Number of points in the second cloud
N_B = 200

# Generate random points
cloudA = np.random.normal(coord1_A, coord2_A, size=(N_A, 2))
cloudB = np.random.normal(coord1_B, coord2_B, size=(N_B, 2))

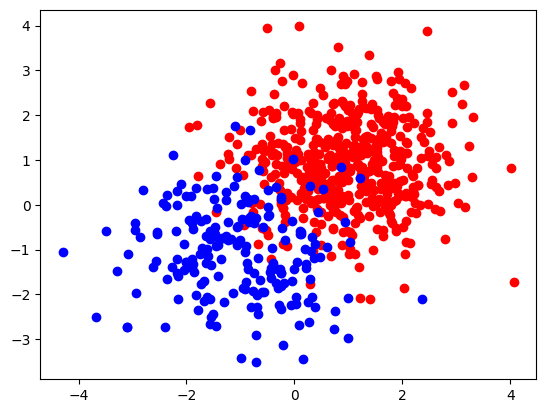
Voici une visualisation des deux nuages (en supposant que vous avez nommé les deux nuages de points cloudA et cloudB) sous forme de nuage de points en utilisant la bibliothèque matplotlib.

# Needed imports
import matplotlib.pyplot as plt



# Plot the clouds
plt.scatter(cloudA[:, 0], cloudA[:, 1], c='r')
plt.scatter(cloudB[:, 0], cloudB[:, 1], c='b')

# Display all open figures
plt.show()

1.3 — Préparer le jeu de données et le diviser en ensemble d’entraînement et de test

Nous allons maintenant préparer le jeu de données. Les étapes suivantes sont nécessaires :

• Pour chaque nuage, préparer un vecteur d’étiquettes, en utilisant une valeur entière différente pour chacun, par exemple 0 pour le nuage A et 1 pour le nuage B.
• En utilisant la fonction np.vstack et/ou np.hstack (empilement vertical/horizontal), concaténer les deux nuages en un tableau X et le vecteur d’étiquettes en un tableau (1D) y.
• Générer un vecteur de permutations des indices du tableau concaténé en utilisant np.random.permutation().
• Utiliser cette permutation pour diviser X et y en X_train,y_train et X_test,y_test avec un ratio de 80 % pour l’entraînement / 20 % pour le test.
• Vérifier les formes des ensembles d’entraînement et de test générés.

a = np.array([[1, 2], [3,4]])
b = np.array([[5,6], [7,8]])
c = np.vstack([a, b])
print(c)

[[1 2]
 [3 4]
 [5 6]
 [7 8]]

a = np.array([[1, 2], [3,4]])
b = np.array([[5,6], [7,8]])
c = np.hstack([a, b])
print(c)

[[1 2 5 6]
 [3 4 7 8]]

a = np.array([[1, 2, 3,4]])
permuted = np.random.permutation(4)
print(permuted)

[2 0 3 1]

# Needed imports
import numpy as np



# For each cloud, prepare a vector of labels, using a different integer value for each.
y_A = np.zeros(N_A) # we will assign the value "0" to cloud A 
y_B = np.ones(N_B) # we will assign the value "1" to cloud B

# Using the `np.vstack` and `np.hstack` functions, concatenate the two clouds into one array `X` and the labels vector into a (1D) array `y`
X = np.vstack([cloudA, cloudB])
y = np.hstack([y_A, y_B])

# Generate a vector of permutations of the indices of the concatenated array using `np.random.permutation()`
permuted = np.random.permutation(N_A+N_B)

# Permute the rows of `X` and `y` using the generated permutation
X = X[permuted]
y = y[permuted]

# Split `X` and `y` into `X_train,y_train` and `X_test,y_test` with ratios 80 percent for train / 20 percent for test.
split_train = int(0.8*(N_A+N_B))
X_train = X[:split_train]
y_train = y[:split_train]
X_test = X[split_train:]
y_test = y[split_train:]

# Check the shapes of the resulting arrays
print(f"Number of samples in train set: {np.shape(y_train)}")
print(f"Number of samples in test set: {np.shape(y_test)}")

2 — Apprentissage supervisé avec $k$-plus proches voisins

Dans cet exercice, nous allons implémenter la prédiction sur un jeu de données de test en utilisant un $k$-NN sur un jeu de données d’entraînement. Vous pouvez consulter le matériel de cours pour comprendre le principe de l’algorithme. Les différentes étapes du $k$-NN sont les suivantes.

Pour chaque échantillon du jeu de test :

1. Calculer toutes les distances paires entre l’échantillon et le jeu d’entraînement.
2. Extraire les étiquettes des k plus petites distances.
3. Assigner l’étiquette selon celle qui est la plus représentée parmi les étiquettes associées aux $k$ plus petites distances (vote majoritaire).

Nous utiliserons la distance euclidienne pour considérer les distances entre échantillons. Vous pouvez tester votre fonction sur les jeux d’entraînement / test générés dans la première partie.

La fonction doit avoir la signature suivante :

# Needed imports
import numpy as np
from typing import List


def kNN (k: int, X_train: np.array, y_train: List[int], X_test: np.array) -> np.array:
    
    """
        k-NN prediction on a test set using a training dataset.
        In: 
            * k:       Number of neighbours to consider. 
            * X_train: Training dataset, numpy array with N (samples) rows and d (features) columns.
            * y_train: List of N labels associated with each example in X_train.
            * X_test:  Test dataset, numpy array with M (samples rows and d (features) columns.
        Out:
            * List of M labels associated with each example in X_test according to the k nearest neighbours with X_train.
    """

    pass

Testez votre fonction avec k = 3 en utilisant les jeux d’entraînement et de test que vous avez générés dans la partie précédente.

# Needed imports
import numpy as np
from typing import List



def kNN (k: int, X_train: np.array, y_train: List[int], X_test: np.array) -> np.array:
    
    """
        k-NN prediction on a test set using a training dataset.
        In: 
            * k:       Number of neighbours to consider. 
            * X_train: Training dataset, numpy array with N (samples) rows and d (features) columns.
            * y_train: List of N labels associated with each example in X_train.
            * X_test:  Test dataset, numpy array with M (samples rows and d (features) columns.
        Out:
            * List of M labels associated with each example in X_test according to the k nearest neighbours with X_train.
    """

    # Inner function to compute the Euclidean distance between two points
    def euclidean_distance (x1, x2):
        """Compute the Euclidean distance between two points."""
        return np.sqrt(np.sum((x1 - x2) ** 2))

    # Predict for all data
    predictions = []
    for x_test in X_test:

        # Compute distances between the test point and all training points
        distances = [euclidean_distance(x_test, x_train) for x_train in X_train]

        # Get the indices of the k nearest neighbors
        k_indices = np.argsort(distances)[:k]

        # Get the labels of the k nearest neighbors
        k_labels = [y_train[i] for i in k_indices]

        # Determine the most common label (majority vote) using numpy
        unique_labels, counts = np.unique(k_labels, return_counts=True)
        most_common = unique_labels[np.argmax(counts)]
        predictions.append(most_common)
    
    # Return this in an array
    return np.array(predictions)



# Test the k-NN 
# Assuming that X_train, y_train, X_test have been defined in the previous exercize 
k = 3
predictions = kNN(k, X_train, y_train, X_test)
print("Predicted labels:", predictions)

Vous pouvez utiliser le snippet suivant pour vérifier la précision du $k$-NN entraîné. La précision correspond à la proportion de réponses correctes.

# Percentage of correct predictions
accuracy = np.mean(predictions == y_test)
print(f"Accuracy of k-NN with k={k}: {accuracy}")

Avec les paramètres qui génèrent le jeu de données de la correction ci-dessus, vous devriez obtenir une précision d’environ 0.93.

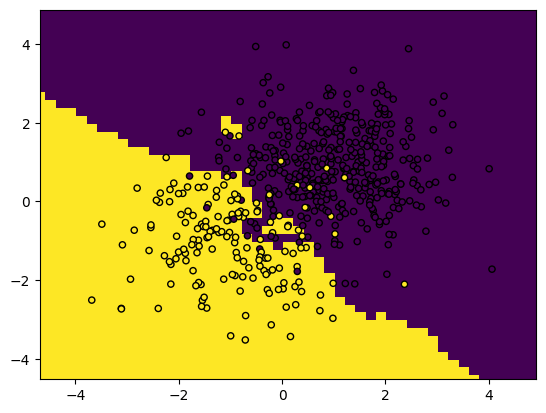
Vous pouvez également tracer les frontières de décision avec ce snippet. Cela montre les zones qui, selon la position des points d’entraînement, seront classées comme classe A ou B.

# Needed imports
from matplotlib.colors import ListedColormap
import numpy as np



def plot_boundaries (classifier, X, Y, h=0.2):

    # Create color maps
    x0_min, x0_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x1_min, x1_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    x0, x1 = np.meshgrid(np.arange(x0_min, x0_max, h), np.arange(x1_min, x1_max, h))
    dataset = np.c_[x0.ravel(), x1.ravel()]
    Z = kNN(k, X, Y, dataset)

    # Put the result into a color plot
    Z = Z.reshape(x0.shape)
    plt.figure()
    plt.pcolormesh(x0, x1, Z)

    # Plot also the training points
    plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolor='k', s=20)
    plt.xlim(x0.min(), x0.max())
    plt.ylim(x1.min(), x1.max())

    # Display the plot
    plt.show()


# Call the function with your training set
plot_boundaries(predictions, X_train, y_train)

3 — $k$-means clustering

Dans cet exercice, nous allons implémenter l’algorithme $k$-means depuis zéro. Vous pouvez consulter le matériel de cours) pour comprendre le principe de l’algorithme.

Les différentes étapes de $k$-means sont les suivantes :

1. Initialiser aléatoirement les centroïdes
2. Calculer l’assignation actuelle des clusters.
3. Mettre à jour les centroïdes.
4. Calculer la qualité actuelle de l’ajustement (GoF).
5. Répéter à partir de l’étape 2 jusqu’à convergence (GoF suffisamment petit).

La fonction doit avoir la signature suivante :

from typing import List, Tuple

def k_means (k: int, X_train: np.array, X_test: np.array,max_iters:int, tol: float) -> Tuple[np.array, np.array]:

    """
        Cluster assignments on a test set according to clusters defined using k-means clustering on a training dataset.
        In: 
            * k:         Number of clusters to consider.
            * X_train:   Training dataset, numpy array with N (samples) rows and d (features) columns.
            * X_test:    Test dataset, numpy array with M (samples rows and d (features) columns.
            * max_iters: Maximum number of iterations to run the k-means algorithm.
            * tol:       Convergence tolerance for centroid changes.
        Out:
            * List of M cluster assignements associated with each example in X_test.
            * Cluster centroids as a numpy array.
    """

    pass

Testez votre fonction avec k = 2 en utilisant les jeux d’entraînement et de test que vous avez générés.

# Needed imports
import numpy as np
from typing import List, Tuple


def k_means (k: int, X_train: np.array, X_test: np.array,max_iters:int, tol: float) -> Tuple[np.array, np.array]:

    """
        Cluster assignments on a test set according to clusters defined using k-means clustering on a training dataset.
        In: 
            * k:         Number of clusters to consider.
            * X_train:   Training dataset, numpy array with N (samples) rows and d (features) columns.
            * X_test:    Test dataset, numpy array with M (samples rows and d (features) columns.
            * max_iters: Maximum number of iterations to run the k-means algorithm.
            * tol:       Convergence tolerance for centroid changes.
        Out:
            * List of M cluster assignements associated with each example in X_test.
            * Cluster centroids as a numpy array.
    """

    # Inner function for initialization of centroids
    def initialize_centroids (X: np.array, k: int) -> np.array:
        """Randomly initialize k centroids from the dataset."""
        indices = np.random.choice(X.shape[0], k, replace=False)
        return X[indices]

    # Inner function for assigning clusters to centroids
    def assign_clusters (X: np.array, centroids: np.array) -> np.array:
        """Assign each data point to the nearest centroid."""
        distances = np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)
        return np.argmin(distances, axis=1)

    # Inner function for updating centroids
    def update_centroids(X: np.array, labels, k: int) -> np.array:
        """Compute new centroids as the mean of points in each cluster."""
        return np.array([X[labels == i].mean(axis=0) for i in range(k)])

    # Inner function for fitting k-means
    def fit_k_means (X: np.array, k: int, max_iters: int, tol: float) -> np.array:
        """Run the {k-means algorithm to find cluster centroids."""
        centroids = initialize_centroids(X, k)
        for _ in range(max_iters):
            labels = assign_clusters(X, centroids)
            new_centroids = update_centroids(X, labels, k)
            if np.linalg.norm(centroids - new_centroids) < tol:
                break
            centroids = new_centroids
        return centroids

    # Fit k-means on the training set
    centroids = fit_k_means(X_train, k, max_iters, tol)

    # Assign clusters to the test set
    test_labels = assign_clusters(X_test, centroids)
    return test_labels,centroids

# Test the k-means with the training set
k = 2 # Number of clusters
test_labels, centroids = k_means(k, X_train, X_test, 100, 1e-4)
print("Predicted labels:", test_labels)

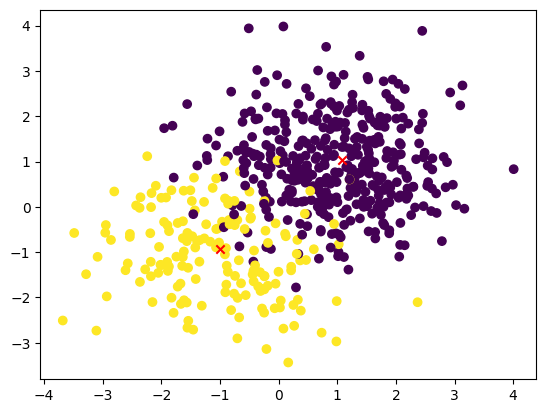
Utilisez ce code pour visualiser le jeu de données avec les centroïdes de clusters ajoutés :

# Needed imports
import matplotlib.pyplot as plt

## Plot
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
plt.scatter(centroids[:, 0], centroids[:, 1], c='r',marker ='x')

5 — Optimisez vos solutions

Ce que vous pouvez faire maintenant est d’utiliser des outils d’IA tels que GitHub Copilot ou ChatGPT, soit pour générer la solution, soit pour améliorer la première solution que vous avez proposée ! Essayez de faire cela pour tous les exercices ci-dessus, pour voir les différences avec vos solutions.

Pour aller plus loin

6 — Matrice de confusion et métriques de performance

Vous pouvez analyser plus en détail la performance d’un algorithme d’apprentissage supervisé en utilisant d’autres outils :

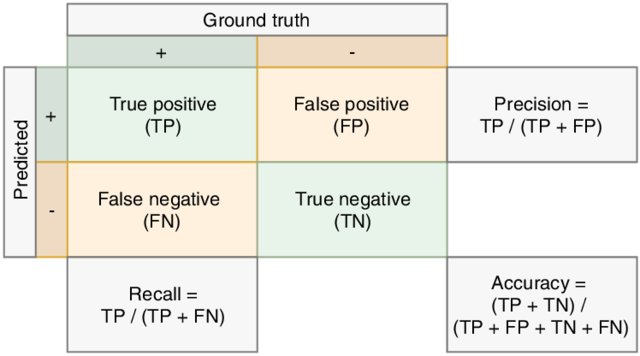
• La matrice de confusion est un comptage (normalisé) des échantillons selon toutes les possibilités de classes prédites et classes réelles. Elle fournit donc des détails sur les erreurs de classification, montrant quelles classes sont plus difficiles que d’autres. Vous pouvez estimer la matrice de confusion en utilisant la fonction confusion_matrix de sklearn.

• Le score de précision est le pourcentage d’exemples correctement classés par rapport à tous les exemples récupérés.

• Le score de rappel est le pourcentage d’exemples correctement classés par rapport à tous les exemples appartenant à une classe donnée.

• Le score f1 est la moyenne harmonique de la précision et du rappel.

Voici une illustration de la précision et du rappel :

Ces trois métriques peuvent être calculées à partir des fonctions du module sklearn.metrics. Une manière simple de les afficher toutes est d’imprimer le rapport de classification.

Pour aller encore plus loin

On dirait que cette section est vide !

Y a-t-il quelque chose que vous auriez aimé voir ici ? Faites-le nous savoir sur le serveur Discord ! Peut-être pouvons-nous l’ajouter rapidement. Sinon, cela nous aidera à améliorer le cours pour l’année prochaine