Representing graphs
Reading time5 minEn bref
Résumé de l’article
Dans cet article, vous apprendrez des solutions pour représenter des graphes dans la mémoire d’un ordinateur. Après la vidéo, nous vous présenterons la structure de graphe que vous manipulerez dans le projet PyRat.
Points clés
-
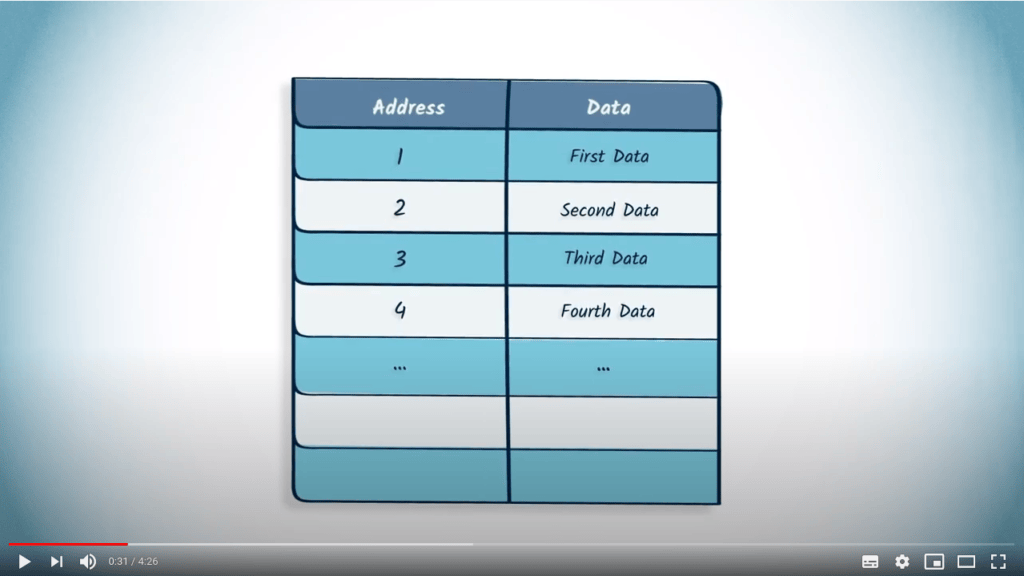
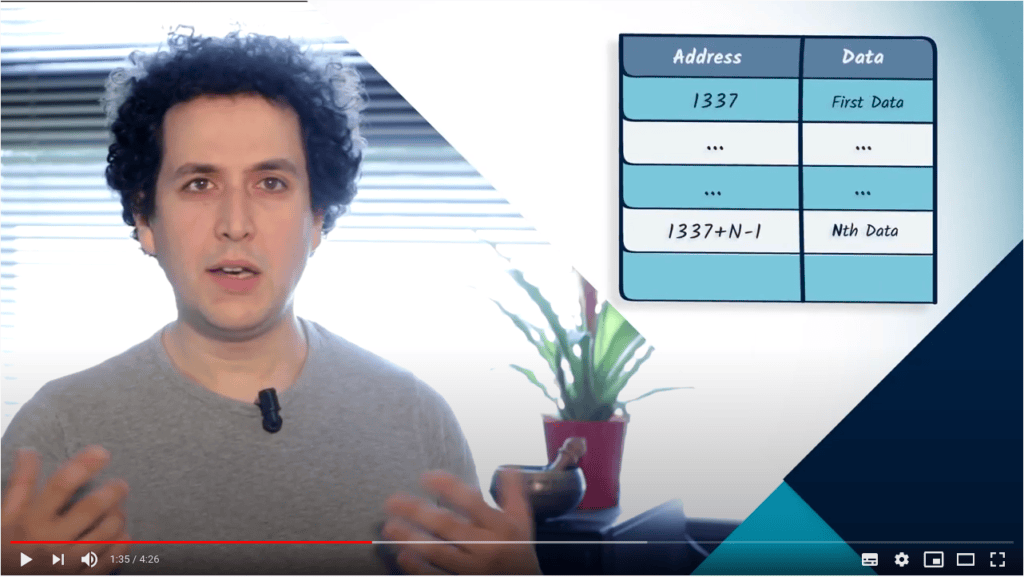
La matrice d’adjacence d’un graphe peut être représentée en mémoire à l’aide d’un tableau.
-
Les listes et les dictionnaires sont également des solutions pour représenter un graphe en mémoire.
-
Chaque représentation a ses propres avantages et inconvénients.
-
Dans PyRat, la représentation d’un graphe est abstraite dans un objet.
Contenu de l’article
1 — Vidéo
Veuillez regarder la vidéo ci-dessous. Vous pouvez également lire la transcription si vous préférez.
2 — La représentation d’un graphe dans PyRat
Dans le logiciel PyRat, le graphe est encapsulé dans un objet, c’est-à-dire une structure complexe qui vous fournit une interface pratique pour le manipuler. En termes simples, vous n’avez pas un accès direct à la matrice d’adjacence, à la liste ou au dictionnaire qui stocke le graphe en mémoire. À la place, vous avez accès à de nombreux attributs et méthodes, qui vous permettent de manipuler le graphe sans entrer dans les détails de son implémentation.
Plus précisément, soit g une instance d’un Graph PyRat.
Vous pouvez utiliser les éléments suivants :
g.vertices– Vous donne une liste des sommets du graphe.g.nb_vertices– Vous donne le nombre de sommets dans le graphe.g.edges– Vous donne la liste des arêtes du graphe.g.nb_edges– Vous donne le nombre d’arêtes dans le graphe.g.add_vertex(v)– Ajoute le sommetvau graphe.g.add_edge(v1, v2, w)– Ajoute une arête de poidswentrev1etv2.g.get_neighbors(v)– Vous donne les voisins devdans le graphe.g.get_weight(v1, v2)– Vous donne le poids de l’arête entrev1etv2.g.remove_vertex(v)– Supprime le sommetvet toutes les arêtes qui y sont attachées du graphe.g.remove_edge(v1, v2)– Supprime l’arête entrev1etv2du graphe.g.is_connected()– Indique si le graphe est connexe.g.has_edge(v1, v2)– Indique si une arête existe entre les sommetsv1etv2.g.edge_is_symmetric(v1, v2)– Indique si l’arête dev1versv2peut être utilisée pour aller dev2àv1.g.minimum_spanning_tree()– Vous donne un arbre couvrant minimal pour le graphe.g.as_dict()– Vous donne une représentation dictionnaire du graphe.g.as_numpy_ndarray()– Vous donne une représentation matricielle du graphe (comme unnumpy.ndarray).g.as_torch_tensor()– Vous donne une représentation matricielle du graphe (comme untorch.tensor).
En pratique, un labyrinthe PyRat est une instance de la classe Maze, qui hérite de Graph.
Par conséquent, il possède quelques attributs supplémentaires (par exemple, une width et une height en nombre de cellules) et des méthodes (par exemple, coords_difference(v1, v2) pour obtenir la différence selon les axes largeur et hauteur, i_exists(v) pour vérifier qu’une cellule existe dans le labyrinthe).
Consultez la documentation de Maze.py pour toutes les informations !
Vous voyez, à aucun moment vous n’avez besoin de connaître la structure sous-jacente pour utiliser le graphe dans votre projet. C’est très pratique si le développeur de PyRat décide un jour de changer cette structure pour une raison quelconque. En effet, tant que l’interface reste inchangée, les codes des utilisateurs continueront de fonctionner.
Il existe de nombreuses bibliothèques en ligne qui fournissent de telles interfaces pour utiliser des graphes. Quel que soit le langage que vous utilisez, il est toujours judicieux de vérifier les implémentations existantes avant de réimplémenter une structure à partir de zéro !
Pour aller plus loin
3 — Plus de détails sur la solution basée sur les listes
Nous avons vu précédemment qu’une matrice d’adjacence est un objet pratique pour représenter un graphe en mémoire.
Cependant, dans la plupart des cas, les graphes sont des objets clairsemés, c’est-à-dire que le nombre d’arêtes existantes est faible comparé au nombre d’arêtes d’un graphe complet. Une implication directe est que la plupart des entrées de la matrice d’adjacence sont des zéros. Puisque le nombre d’éléments dans une matrice d’adjacence est égal au carré de l’ordre du graphe, cela peut rapidement conduire à une grande consommation d’espace mémoire.
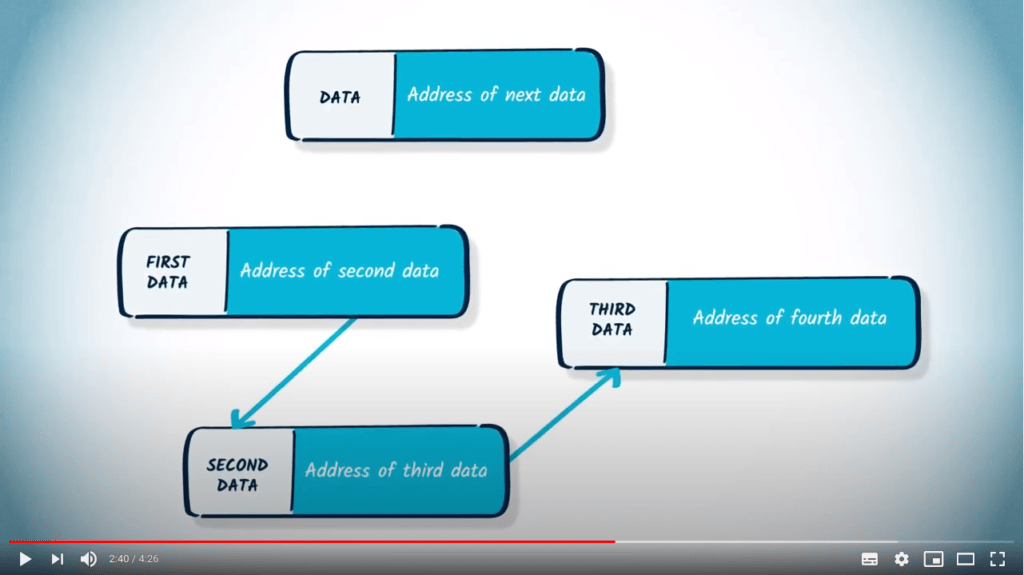
Une solution possible pour contourner ce problème est d’utiliser une structure de données différente : une liste de listes. Appelons un tel objet $L = (l_1, \dots, l_n)$, avec $l_1, \dots, l_n$ étant des listes. Dans cette structure, $l_i$ $(i \in [1, n])$ représentera les arêtes accessibles depuis le sommet $i$.
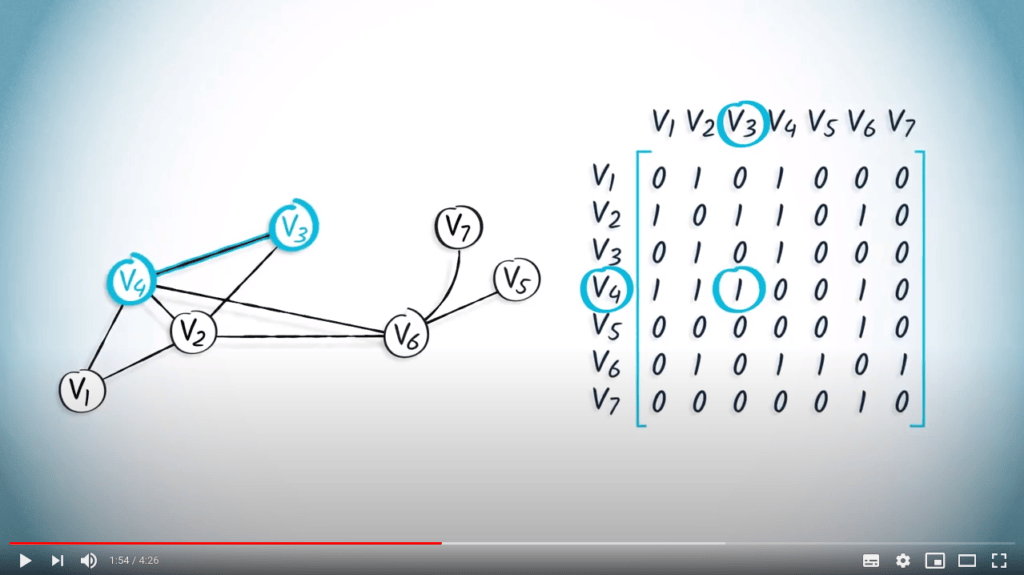
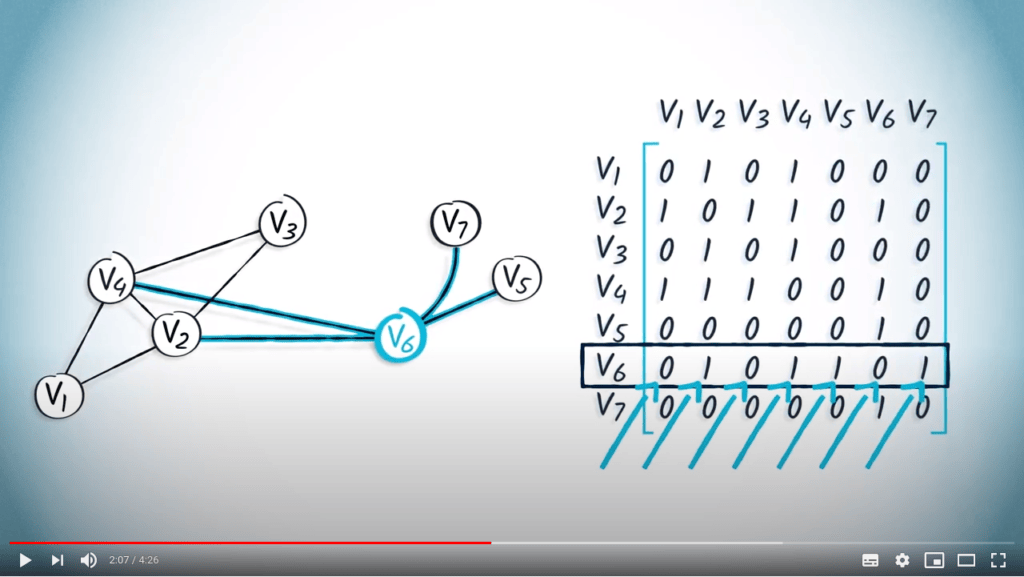
Par exemple, considérons la matrice d’adjacence suivante : $${\bf A} = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{pmatrix}$$
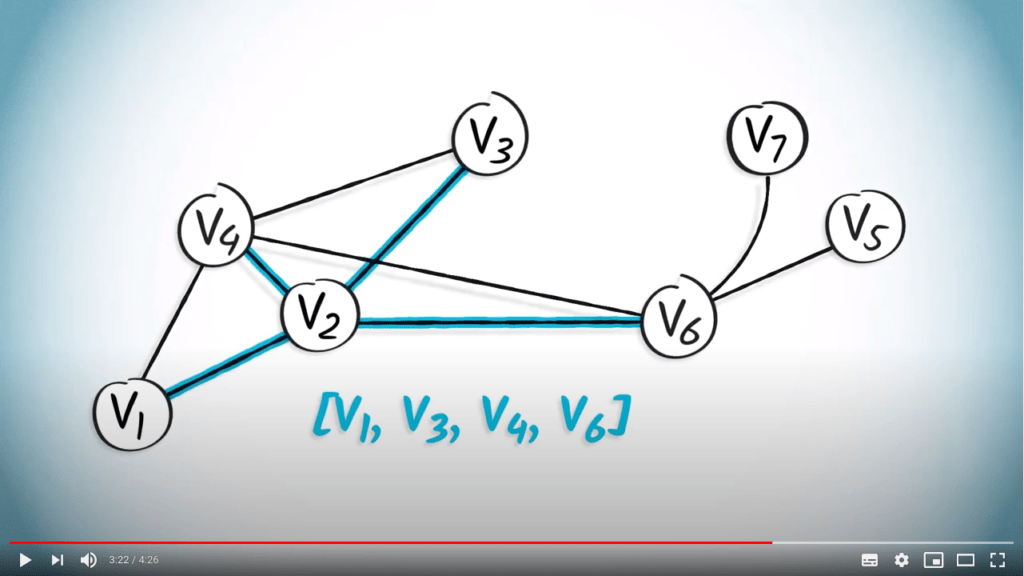
En supposant que les sommets soient étiquetés de 1 à $n$, cette matrice est équivalente à la liste $L = ( (2, 4) , (1, 3, 4, 6), (2, 4), (1, 2, 3, 6), (6), (2, 4, 5, 7), (6) )$.
On peut rapidement remarquer que le nombre de nombres stockés est passé de $n^2$ = 49 à 18.
Bien que cette solution économise de l’espace mémoire, elle souffre de différentes limitations :
-
Vérifier l’existence d’une arête $\{i, j\}$ nécessite de parcourir tous les éléments de la liste $l_i$ pour vérifier si $j$ en fait partie. Cela peut prendre du temps si $i$ a beaucoup de voisins. En comparaison, faire la même vérification avec une matrice d’adjacence ${\bf A}$ ne prend qu’une seule opération, car il suffit de vérifier que ${\bf A}[i, j] \neq 0$.
-
Ce n’est pas aussi facile à étendre aux graphes pondérés. Dans le cas des matrices d’adjacence, les entrées représentent le poids associé à l’arête. Ici, les entrées sont des indices d’éléments non nuls, qui ne peuvent pas être modifiés sans créer/supprimer des arêtes. Une solution possible est de remplacer les listes d’indices $l_i = (j, k, \dots)$ par des listes de couples $l_i = ( (j, w_j), (k, w_k), \dots )$, où $w_j$ est le poids de l’arête $\{i, j\}$.
Pour aller encore plus loin
-
Understanding the efficiency of GPU algorithms for matrix-matrix multiplication.
Un article de recherche illustrant l’une des principales raisons pour lesquelles les matrices sont fréquemment utilisées.
-
Graph Processing on FPGAs: Taxonomy, Survey, Challenges.
Un article de recherche illustrant l’utilisation de matériel spécifique (ici, FPGA) pour le traitement de grands graphes.