Practical activity

Présentation & objectifs

Dans cette activité, vous devrez développer une solution pour attraper un seul morceau de fromage dans un labyrinthe sans boue. Ici, nous choisissons de nous concentrer sur deux algorithmes : la recherche en largeur (breadth-first search) et la recherche en profondeur (depth-first search).

Contenu de l’activité

1 — Recherche en profondeur (DFS)

1.1 — Préparation

Avant de commencer, créons d’abord les fichiers nécessaires dans l’espace de travail :

• pyrat_workspace/players/DFS.py – Dupliquez le fichier TemplatePlayer.py, et renommez-le en DFS.py. Ensuite, comme dans la session précédente, renommez la classe en DFS.

• pyrat_workspace/games/visualize_DFS.ipynb – Créez un fichier qui lancera une partie avec un joueur DFS, dans un labyrinthe sans boue (argument mud_percentage), et un seul morceau de fromage (argument nb_cheese). Optionnellement, vous pouvez définir une random_seed et une trace_length. Vous devriez vous inspirer des autres fichiers dans le sous-répertoire games que vous avez rencontrés lors de la session précédente.

  Essayez de le faire vous-même d’abord. Si vous avez des difficultés, voici la correction :

  Correction

  • Cliquez ici pour télécharger la correction de visualize_DFS.ipynb.

1.2 — La méthode de parcours

1.2.1 — Implémentation

Pour écrire un algorithme DFS, nous devons effectuer un parcours. Créons une fonction pour cela. Copiez-collez le morceau de code suivant dans votre fichier DFS.py, en tant que méthode de la classe DFS :

def traversal ( self:   Self,
                graph:  Graph,
                source: Integral
              ) ->      Tuple[Dict[Integral, Integral], Dict[Integral, Optional[Integral]]]:

    """
        This method performs a DFS traversal of a graph.
        It returns the explored vertices with associated distances.
        It also returns the routing table, that is, the parent of each vertex in the traversal.
        In:
            * self:   Reference to the current object.
            * graph:  The graph to traverse.
            * source: The source vertex of the traversal.
        Out:
            * distances:     The distances from the source to each explored vertex.
            * routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
    """

    # Your code here

Remplissez maintenant cette méthode pour qu’elle effectue une recherche en profondeur, comme décrit dans la documentation fournie. Veuillez vous assurer que les variables retournées ont les types indiqués.

1.2.2 — Tests

Pour vous assurer que votre code fonctionne, il est essentiel de le tester. En fait, on distingue trois grandes familles de tests :

• Debug – Exécutez fréquemment votre programme, afin de pouvoir détecter facilement une erreur. En effet, il est plus facile de trouver une erreur dans les dernières lignes de code écrites que dans tout le programme.

• Tests statistiques – Comme mentionné dans la session précédente, ces tests peuvent vous aider à prouver des propriétés sur vos programmes. Ils ne sont cependant pas destinés à faire fonctionner votre code.

• Tests unitaires – Les tests unitaires sont une manière automatisée de déboguer. L’idée est de définir plusieurs entrées pour une fonction donnée, pour lesquelles vous connaissez la sortie attendue (ou des propriétés de la sortie), et d’appeler cette fonction avec ces entrées. Si toutes les sorties produites correspondent aux sorties attendues (ou valident les propriétés), alors on peut avoir une bonne confiance que la fonction est correcte. Un bon ensemble de tests unitaires devrait essayer de couvrir tous les cas d’exécution possibles de la fonction (ex. toutes les branches d’une condition if). Il doit garantir que la fonction fonctionne dans les cas d’usage standard, mais aussi dans les cas limites.

Dans cette activité, nous vous fournissons des tests unitaires, afin que vous puissiez vérifier que votre code fonctionne correctement. Plus tard, vous devrez développer vos propres tests, alors regardons ceux déjà fournis.

Commencez par créer un sous-répertoire pyrat_workspace/tests. Puis, téléchargez le fichier de test suivant pour le joueur DFS, et placez-le dans ce répertoire.

Si vous avez bien compris l’algorithme de recherche en profondeur, vous devriez voir qu’il existe plusieurs solutions possibles, selon l’ordre dans lequel les sommets voisins sont explorés. Pour cette raison, nous ne pouvons pas directement créer un test pour vérifier que, pour un graphe donné $G$, on obtient une table de routage particulière. À la place, nous allons évaluer des propriétés de la solution produite par la fonction traversal :

• Les sorties ont les types attendus.
• Tous les sommets sont visités.
• La table de routage est un arbre, avec la racine correspondant au début du parcours.
• Les distances trouvées sont correctes, c’est-à-dire strictement positives et croissantes, sauf pour le sommet de départ qui doit être 0.

Regardons le fichier de test fourni. D’abord, les tests unitaires doivent être définis dans une classe héritant de unittest.TestCase comme suit :

class DFSTests (unittest.TestCase):

Ensuite, pour chaque méthode que vous souhaitez tester, vous devez créer une fonction dédiée. Par exemple, ici, nous voulons tester la méthode traversal de la classe DFS, alors créons une méthode nommée test_traversal :

def test_traversal ( self: Self
                   ) ->    None:

Dans cette méthode, nous allons vérifier les points listés ci-dessus. Pour avoir une plus grande confiance dans les tests, nous allons les vérifier sur plusieurs labyrinthes aléatoires. Pour générer ces labyrinthes, nous utilisons une des classes PyRat qui fait cela :

# Constants
NB_GRAPHS = 10
WIDTHS = [2, 30]
HEIGHTS = [2, 30]
CELL_PERCENTAGES = [20.0, 100.0]
WALL_PERCENTAGES = [20.0, 100.0]
MUD_PERCENTAGE = 0.0

# Test on several graphs
for i in range(NB_GRAPHS):
    
    # Instantiate the player
    player = DFS()

    # Generate a random maze
    # We use a fixed random seed for reproducibility of tests
    rng = random.Random(i)
    maze = BigHolesRandomMaze(width = rng.randint(WIDTHS[0], WIDTHS[1]),
                              height = rng.randint(HEIGHTS[0], HEIGHTS[1]),
                              cell_percentage = rng.uniform(CELL_PERCENTAGES[0], CELL_PERCENTAGES[1]),
                              wall_percentage = rng.uniform(WALL_PERCENTAGES[0], WALL_PERCENTAGES[1]),
                              mud_percentage = MUD_PERCENTAGE,
                              random_seed = i)

Ensuite, nous exécutons la fonction traversal sur ce labyrinthe, à partir d’un sommet aléatoire :

# Choose a random starting vertex
start_vertex = rng.choice(maze.vertices)

# Perform the traversal
distances, routing_table = player.traversal(maze, start_vertex)

Maintenant que tout est prêt, faisons les tests ! D’abord, vous avez été invité à vous assurer que les sorties de traversal ont un certain type :

# Check the output type for distances
# It should be a dictionary with integer keys and integer values
self.assertTrue(isinstance(distances, Dict))
self.assertTrue(all(isinstance(k, Integral) for k in distances.keys()))
self.assertTrue(all(isinstance(v, Integral) for v in distances.values()))

# Check the output type for the routing table
# It should be a dictionary with integer keys and integer or None values
self.assertTrue(isinstance(routing_table, Dict))
self.assertTrue(all(isinstance(k, Integral) for k in routing_table.keys()))
self.assertTrue(all(isinstance(v, (type(None), Integral)) for v in routing_table.values()))

Ensuite, nous voulons vérifier que tous les sommets ont été visités. Équivalemment, nous pouvons vérifier que tous les sommets ont une distance au sommet de départ lors de la recherche.

# All vertices should be visited
# Equivalently, the distances should have the same keys as the maze vertices
self.assertEqual(sorted(set(distances.keys())), sorted(maze.vertices))

Maintenant, assurons-nous que le sommet de départ est la racine de l’arbre, et qu’aucun autre sommet ne pourrait être racine :

# Check that the start vertex is the only tree root
self.assertEqual(routing_table[start_vertex], None)
self.assertTrue(all(routing_table[v] is not None for v in routing_table.keys() if v != start_vertex))
self.assertEqual(distances[start_vertex], 0)
self.assertTrue(all(distances[v] > 0 for v in distances.keys() if v != start_vertex))

Enfin, vérifions que nous avons un arbre valide. Pour détecter un arbre, nous devons pouvoir atteindre la racine depuis n’importe quel sommet. En même temps, nous pouvons vérifier que la distance à un sommet est toujours supérieure à la distance à son parent :

# We check that the routing table is a tree
# Also we check that associated distances are decreasing as we go to the root
for vertex in routing_table:

    # We check that the parent is closer to the root
    if routing_table[vertex] is not None:
        self.assertTrue(distances[routing_table[vertex]] < distances[vertex])
    
    # We ckeck that we can reach the root from any vertex
    path = [vertex]
    while routing_table[path[-1]] is not None:
        self.assertTrue(routing_table[path[-1]] not in path)
        path.append(routing_table[path[-1]])

Maintenant, lancez les tests en exécutant la commande en bas du fichier. Si tout est correct, vous devriez observer la sortie suivante :

test_traversal (__main__.DFSTests)
This method tests the 'traversal' method. ... ok

----------------------------------------------------------------------
Ran 1 test in 2.453s

OK

1.3 — Utilisation de la table de routage

1.3.1 — Implémentation

Maintenant que vous avez un parcours fonctionnel, écrivons une méthode qui exploite la table de routage pour retourner la série de positions à suivre pour atteindre un sommet donné. Copiez-collez le morceau de code suivant dans votre fichier DFS.py en tant que méthode de la classe DFS :

def find_route ( self:          Self,
                 routing_table: Dict[Integral, Optional[Integral]],
                 source:        Integral,
                 target:        Integral
               ) ->             List[Integral]:

    """
        This method finds the route from the source to the target using the routing table.
        In:
            * self:          Reference to the current object.
            * routing_table: The routing table.
            * source:        The source vertex.
            * target:        The target vertex.
        Out:
            * route: The route from the source to the target.
    """

    # Your code here

Remplissez maintenant cette fonction pour qu’elle retourne la route du sommet source au sommet cible. Encore une fois, assurez-vous que votre code respecte les types.

1.3.2 — Tests

Maintenant que nous avons écrit une autre méthode, ajoutons quelques tests. Ici, notez que pour une table de routage donnée, des sommets source et cible donnés, il n’y a qu’une seule solution possible. Par conséquent, nous pouvons appeler la méthode sur des scénarios fixes.

Copiez le code suivant dans votre fichier tests_DFS.ipynb, en tant que nouvelle méthode de votre classe DFSTests :

def test_find_route ( self: Self,
                    ) ->    None:
    
    """
        This method tests the 'find_route' method.
        Here, we want to make sure that the output corresponds indeed to a route from the start to the end.
        We are going to check the following:
        - Outputs are of the expected types.
        - The route is a valid path from the start to the end.
        The method will be tested on some controlled examples, where we can easily check the validity of the output.
        In:
            * self: Reference to the current object.
        Out:
            * None.
    """

    # Constants
    INPUTS = [{"routing_table": {0: None, 1: 0, 2: 1, 3: 2, 4: 3},
               "start": 0,
               "end": 4},
              {"routing_table": {0: 2, 1: None, 2: 1, 3: 0, 4: 0, 5: 4, 6: 1},
               "start": 1,
               "end": 6}]

    # Test on several controlled examples
    for i in range(len(INPUTS)):
        
        # Instantiate the player
        player = DFS()

        # Get the input data
        routing_table = INPUTS[i]["routing_table"]
        start = INPUTS[i]["start"]
        end = INPUTS[i]["end"]

        # Find the route
        route = player.find_route(routing_table, start, end)

        # Check the output type
        # It should be a list of integers
        self.assertTrue(isinstance(route, List))
        self.assertTrue(all(isinstance(v, Integral) for v in route))

        # Check that the route is a valid path from the start to the end
        self.assertEqual(route[0], start)
        self.assertEqual(route[-1], end)
        self.assertTrue(all(routing_table[route[j + 1]] == route[j] for j in range(len(route) - 1)))

Ici, nous définissons deux tables de routage à la main, et les utilisons comme entrées pour tester la méthode find_route. Nous aurions pu en définir beaucoup plus, et aussi utiliser des tables de routage valides aléatoires, générées avec la fonction traversal que nous avons développée et validée précédemment.

Dans ces tests, nous effectuons une vérification de type de la sortie, puis vérifions que les parents dans la table de routage apparaissent bien comme prédécesseurs dans la route obtenue. De plus, nous vérifions que la route va bien du début à la fin.

Voici ce que vous devriez obtenir en exécutant le script :

test_find_route (__main__.DFSTests)
This method tests the 'find_route' method. ... ok
test_traversal (__main__.DFSTests)
This method tests the 'traversal' method. ... ok

----------------------------------------------------------------------
Ran 2 tests in 2.798s

OK

1.4 — Mise en place complète

1.4.1 — Implémentation

Maintenant, il ne reste plus qu’à assembler les briques. Voici les modifications que vous devez faire :

• __init__ – Mettez à jour votre fonction __init__ pour déclarer un attribut self.actions = [].

• preprocessing – Pendant le prétraitement, utilisez les méthodes introduites précédemment (self.traversal et self.find_route) pour calculer les actions depuis votre position initiale (game_state.player_locations[self.name]) jusqu’à la position du seul morceau de fromage (game_state.cheese[0]). Ensuite, stockez ces actions dans l’attribut self.actions. Pour obtenir des actions à partir d’une route, la classe Maze fournit une méthode locations_to_actions.

• turn – À chaque tour, vous devez retourner une action depuis self.actions. Il suffit d’extraire la prochaine action à effectuer depuis cet attribut, et de la retourner.

1.4.2 — Tests

Utilisez maintenant votre script visualize_DFS.ipynb pour jouer avec votre joueur ! La vidéo suivante montre un exemple de ce que vous devriez observer :

2 — Recherche en largeur (BFS)

Comme vous pouvez le voir dans la vidéo précédente, le DFS trouve un chemin qui n’est pas exactement le plus court. Nous allons maintenant utiliser un autre algorithme de parcours appelé BFS. Cet algorithme a la propriété de retourner le chemin le plus court dans un graphe non pondéré.

Suivez les mêmes étapes qu’auparavant pour créer un joueur qui suit un chemin trouvé par un algorithme BFS pour attraper le morceau de fromage. Créez un fichier pour lancer une partie, appelé visualize_BFS.ipynb dans le sous-répertoire pyrat_workspace/games, et un fichier joueur appelé BFS.py dans le sous-répertoire pyrat_workspace/players. Pour ce dernier, vous devriez partir d’une copie de votre fichier DFS.py, car il n’y aura pas beaucoup de différences !

N’oubliez pas non plus de tester vos fonctions ! Voici les tests que vous pouvez utiliser pour vous assurer que votre code fonctionne. Notez à quel point ils sont similaires à ceux du DFS. Notez aussi que nous avons ajouté une nouvelle fonction de test pour vérifier que nous trouvons bien les chemins les plus courts, sur quelques exemples contrôlés pour lesquels une seule table de routage est solution du parcours.

La vidéo suivante montre un exemple de ce que vous devriez observer :

3 — Comparaison avec les aléatoires

Maintenant que vous avez deux nouveaux joueurs, il serait intéressant de les comparer avec les joueurs aléatoires que vous avez développés lors de la session précédente. Adaptez (et renommez) le script de jeu compare_all_randoms.ipynb pour intégrer les joueurs DFS et BFS dans l’analyse.

Essayez également de répondre aux questions suivantes :

• Est-ce que DFS est significativement meilleur que le meilleur programme RandomX que vous avez écrit ?
• Est-ce que BFS est significativement meilleur que DFS ?

Pour aller plus loin

4 — Factoriser les codes

Comme vous l’avez peut-être remarqué, les parcours BFS et DFS sont extrêmement similaires. En fait, la structure de données utilisée détermine l’ordre dans lequel les sommets sont explorés. En effet, en utilisant une FIFO, le parcours effectue une recherche en largeur. En utilisant une LIFO, le parcours effectue une recherche en profondeur.

Ainsi, en généralisant un peu, un parcours peut être vu comme un algorithme global qui, à un moment donné, doit :

• Créer une structure de données.
• Ajouter un élément à la structure de données.
• Extraire un élément de la structure de données.

Le cadre de la programmation orientée objet rend cela assez pratique dans ce genre de situations, via un mécanisme appelé “héritage”. L’idée est d’avoir une classe de base qui factorise le code commun, et des sous-classes qui spécialisent les particularités. Schématiquement, nous pourrions organiser notre code comme suit :

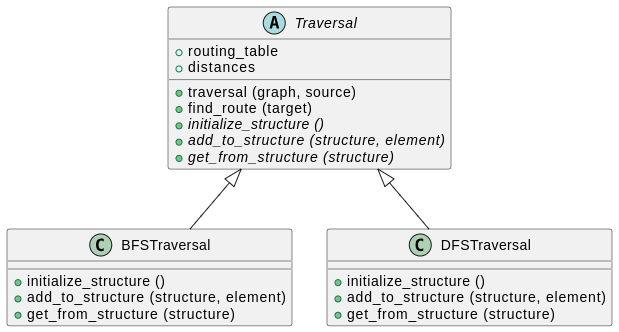
Le diagramme ci-dessus est une version simplifiée de ce que nous appelons un “diagramme de classes UML”. Il se lit comme suit :

• Nous avons trois classes : Traversal, BFSTraversal et DFSTraversal. Traversal ayant son nom en italique, c’est une classe “abstraite”, ce qui signifie qu’elle ne peut pas être instanciée. Elle est là uniquement pour abstraire la notion de parcours d’un graphe, et regroupera les aspects communs à tous les parcours.
• La classe Traversal a deux attributs (tous définis par la méthode traversal) : routing_table et distances.
• La classe Traversal a cinq méthodes : traversal, find_route, initialize_structure, add_to_structure et get_from_structure. Notez que les trois dernières sont en italique. Cela signifie qu’elles sont des “méthodes abstraites”, c’est-à-dire qu’elles ne font rien et doivent être implémentées dans les classes enfants.
• Les flèches signifient que les classes BFSTraversal et DFSTraversal héritent de Traversal. Elles auront donc accès à tous les attributs et méthodes définis dans Traversal.
• Notez que ces deux classes redéfinissent les méthodes abstraites dans Traversal pour les rendre utilisables.

Avec cette organisation, vous pouvez instancier bfs = BFSTraversal() et appeler la méthode bfs.traversal(...). Si traversal appelle initialize_structure, alors c’est l’implémentation de initialize_structure dans BFSTraversal qui sera appelée. De même, vous pouvez instancier dfs = DFSTraversal() et appeler la méthode dfs.traversal(...). Dans ce cas, traversal utilisera l’implémentation de initialize_structure dans DFSTraversal. Comme vous le voyez, le même code dans la fonction traversal se comportera donc différemment, car il a été spécialisé par les classes enfants.

Passons à la pratique :

• Tout d’abord, téléchargez cette archive, et extrayez son contenu dans un nouveau sous-répertoire pyrat_workspace/utils. Cette archive contient les codes correspondant aux trois classes du diagramme ci-dessus.

• Ensuite, téléchargez ce fichier joueur, qui contient un joueur pouvant effectuer un parcours ou l’autre. Placez ce fichier dans votre sous-répertoire pyrat_workspace/players.

  Information

  Notez que les fichiers dans le sous-répertoire pyrat_workspace/utils sont importés par TraversalPlayer.py comme suit :

  ​

  Python

  # Add needed directories to the path
  this_directory = os.path.dirname(os.path.realpath(__file__))
  sys.path.append(os.path.join(this_directory, "..", "utils"))

  Cela signifie que, à partir du répertoire contenant TraversalPlayer.py (c’est-à-dire le sous-répertoire pyrat_workspace/players), le répertoire utils peut être trouvé en remontant d’un répertoire. Utiliser cette technique pour importer des modules peut être un peu plus flexible que le code suivant :

  ​

  Python

  # Add needed directories to the path
  sys.path.append(os.path.join("..", "utils"))

  Contrairement au code précédent, cette version cherchera utils dans le répertoire parent, en partant du répertoire contenant le script exécuté.

  En général, dans PyRat, tous les fichiers .py devraient utiliser le premier code, car ils sont destinés à être importés. En revanche, tous les fichiers .ipynb devraient utiliser le second code, car ce sont les fichiers exécutés (et __file__ n’est pas une commande supportée dans ces fichiers).

• Enfin, téléchargez ce fichier de jeu, et ce fichier de jeu Ces jeux créent respectivement une partie avec un joueur BFS et un joueur DFS, utilisant le code factorisé. Placez ces fichiers dans votre sous-répertoire pyrat_workspace/games.

Maintenant, complétez les codes manquants dans Traversal.py, en vous inspirant de ce que vous avez fait précédemment dans l’activité pratique. Les codes dans BFSTraversal.py et DFSTraversal.py sont déjà fonctionnels. Jetez-y un œil pour voir comment ils diffèrent !

Une fois terminé, lancez le script visualize_TraversalPlayer.ipynb pour exécuter des parties avec les nouveaux programmes BFS et DFS.

5 — Limiter l’algorithme de parcours

Pour calculer les informations nécessaires pour se déplacer vers le morceau de fromage, vous n’avez besoin que de déterminer où se trouve ce fromage. Cependant, le BFS est un algorithme 1-à-n, c’est-à-dire qu’il retournera les plus courts chemins d’un emplacement vers tous les autres. Ainsi, tous les calculs effectués après avoir trouvé ce morceau de fromage particulier sont inutiles, car vous n’utiliserez pas les résultats.

Une amélioration possible est donc de modifier l’algorithme de parcours pour qu’il s’arrête dès que toutes les informations nécessaires sont disponibles.

Pour aller au-delà

6 — Un DFS récursif

Puisque DFS utilise une pile, et que les fonctions récursives exploitent la pile d’appels des programmes, cela rend DFS assez facile à coder récursivement. Trouvez des ressources en ligne pour vous guider, et essayez de le faire !

7 — Étendre les tests unitaires

Comme mentionné plus tôt, les tests unitaires que nous vous fournissons dans cette activité correspondent à l’usage standard des fonctions testées. Une chose possible est d’anticiper les erreurs possibles de l’utilisateur, et de produire un message d’erreur adapté.

Vous avez un exemple de cela dans l’archive donnée dans la partie factorisation du code de cette activité. Dans le fichier Traversal.py, dans la méthode find_route, vous pouvez voir le code suivant :

# Debug
assert(self.source is not None) # Should not be called before traversal

Ce test lèvera une exception AssertionError lorsque l’utilisateur essaiera d’appeler find_route avant que la méthode traversal n’ait été utilisée pour définir l’attribut routing_table. Il est alors possible de le tester dans le fichier de test unitaire associé avec :

# Check that an exception is raised if find_route is called before traversal
with self.assertRaises(AssertionError):
    traversal = BFSTraversal()
    traversal.find_route(5)

Dans le même esprit que ce que nous venons de vous présenter, vous pouvez lister les erreurs possibles qu’un utilisateur pourrait faire en utilisant les méthodes traversal et find_route. Puis, mettez à jour vos fichiers BFS.py et DFS.py (ou les fichiers que vous avez écrits dans la section factorisation du code si vous l’avez complétée) pour lever des exceptions lorsque ces erreurs surviennent. Enfin, mettez à jour vos tests unitaires pour vérifier que les exceptions sont bien levées quand il le faut.

8 — L’algorithme IDDFS

Une autre direction que vous pouvez explorer est de programmer un algorithme appelé IDDFS. Cet algorithme combine des aspects des algorithmes BFS et DFS, mais nécessite moins de mémoire que les deux.

• Si vous le souhaitez, vous pouvez essayer d’implémenter cet algorithme (ou peut-être trouver une bibliothèque qui le fait ?).

9 — L’algorithme de Seidel

Alors que le BFS vous donne le plus court chemin d’un sommet vers tous les autres, l’algorithme de Seidel vous donne les plus courts chemins de tous les sommets vers tous les autres dans un graphe non pondéré.

• Si vous le souhaitez, vous pouvez essayer d’implémenter cet algorithme (ou peut-être trouver une bibliothèque qui le fait ?).