Practical activity
Duration2h30Présentation & objectifs
Dans cette activité, vous devrez développer une solution pour attraper un seul morceau de fromage dans un labyrinthe avec de la boue. Pour ce faire, nous proposons d’utiliser l’algorithme de Dijkstra.
Contrairement aux activités précédentes, vous serez beaucoup moins guidé. Nous ne vous fournissons que des indications générales, le reste dépend de vous.
Contenu de l’activité
1 — L’algorithme de Dijkstra
1.1 — Préparez-vous
Avant de commencer, créons d’abord les fichiers dont nous avons besoin dans l’espace de travail :
-
pyrat_workspace/players/Dijkstra.py– Dupliquez le fichierTemplatePlayer.py, et renommez-le enDijkstra.py. Ensuite, comme dans la session précédente, renommez la classe enDijkstra. -
pyrat_workspace/games/visualize_Dijkstra.ipynb– Créez un fichier qui lancera une partie avec un joueurDijkstra, dans un labyrinthe avec de la boue (argumentmud_percentage), et un seul morceau de fromage (argumentnb_cheese). Optionnellement, vous pouvez définir unerandom_seedet unetrace_length. Vous devriez vous inspirer des autres fichiers dans le sous-répertoiregamesque vous avez rencontrés lors de la session précédente. -
pyrat_workspace/tests/tests_Dijkstra.ipynb– En vous inspirant des fichierstest_DFS.ipynbettest_BFS.ipynbrencontrés lors de la session précédente, créez un fichiertest_Dijkstra.ipynb. Ce fichier contiendra les tests unitaires que vous développerez pour tester l’algorithme de Dijkstra.
1.2 — Programmer l’algorithme de Dijkstra
Vous savez déjà que l’algorithme de Dijkstra peut être utilisé pour atteindre cet objectif. Consultez les articles que vous avez étudiés jusqu’à présent, ou d’autres ressources en ligne, comme vous préférez !
Voici quelques points que vous devriez faire.
1.2.1 — Identifier les fonctions
La dernière fois, lors de la programmation des algorithmes BFS et DFS, nous avons identifié quelques sous-programmes que nous pouvions utiliser comme fonctions.
En effet, nous avons créé les méthodes traversal et find_route.
Séparer l’ensemble en ces deux blocs nous a facilité l’écriture des tests unitaires et l’obtention d’un code pleinement fonctionnel.
Vous devriez d’abord prendre un moment pour réfléchir aux méthodes dont vous avez besoin pour écrire l’algorithme de Dijkstra.
Aussi, quelles devraient être leurs entrées ?
Et quelle sortie devraient-elles produire ?
Une fois cela fait, écrivez leurs prototypes (i.e., la ligne def, et un return temporaire si nécessaire) dans votre fichier joueur Dijkstra.py.
1.2.2 — Programmer et tester
Une fois cela fait, il y a deux écoles :
-
Approche classique – La manière la plus courante de développer un programme est de programmer le corps d’une méthode, puis de la tester. Une fois validée, passez à la méthode suivante, etc., jusqu’à ce que toutes les méthodes soient programmées.
-
Développement piloté par les tests – Si vous préférez, avant de coder le contenu de vos méthodes, vous pouvez déjà écrire les tests unitaires dans
test_Dijkstra.ipynb. Cela vous permettra de tester vos méthodes plus fréquemment lors de leur développement, et vous pourrez être convaincu de votre travail lorsqu’elles passent tous les tests que vous avez préalablement conçus.
Dans tous les cas, vous devriez prendre un moment pour réfléchir et lister les tests unitaires que vous souhaitez effectuer. Pour chaque test, nous vous invitons à déterminer s’il correspond à un usage normal, ou à une erreur possible.
Il est important que vous conceviez avec précision des tests qui vous convainquent que votre programme fonctionne comme prévu !
Par exemple, supposons que vous vouliez concevoir un test pour vous assurer que Dijkstra trouve le chemin le plus court dans un graphe pondéré, contrairement à un BFS. Intuitivement, vous voulez créer un graphe fixe, identifier le chemin le plus court à disposition, et vérifier que la sortie de Dijkstra sera égale à ce chemin. Cependant, le choix du graphe que vous utiliserez est très important :
-
Si vous choisissez un labyrinthe dans lequel il n’y a qu’un seul chemin de votre position initiale au morceau de fromage, alors BFS et l’algorithme de Dijkstra trouveront tous deux le chemin correct.
-
De même, s’il n’y a pas de boue sur le chemin le plus court de votre position initiale au morceau de fromage (ou qu’il est toujours plus rapide de traverser cette boue que de l’éviter), alors encore une fois BFS et l’algorithme de Dijkstra trouveront le chemin correct.
1.2.3 — À quoi cela devrait-il ressembler ?
La vidéo suivante vous montre un exemple de ce que vous devriez observer :
N’hésitez pas à comparer avec les autres vidéos de la session précédente pour vérifier les différences.
En particulier, notez que le rat a suivi le chemin [97, 98, 99, 114, ...] au lieu de [97, 112, 113, 114...] pour éviter une boue.
Essayez aussi d’exécuter votre joueur BFS.py sur un labyrinthe pondéré pour vérifier la différence (utilisez l’argument random_seed pour garder le même labyrinthe).
Pour aller plus loin
2 — Comparer avec les autres parcours
Comme précédemment, une chose facile que vous pouvez faire maintenant est de comparer tous les fichiers RandomX.py, DFS.py, BFS.py et Dijkstra.py sur des graphes pondérés.
Vous pouvez adapter le script précédent compare_all_randoms.ipynb (ou quel que soit son nouveau nom) pour cela.
Ensuite, essayez de répondre aux questions suivantes :
-
L’algorithme de Dijkstra réduit-il significativement le nombre de tours nécessaires pour attraper un morceau de fromage comparé à un BFS ?
-
Est-ce le cas pour toutes les valeurs de
mud_percentage? Sinon, quel est le pourcentage minimum de cases séparées par de la boue que vous devez avoir dans le labyrinthe pour que cela soit significatif ? -
Cela dépend-il de l’option
mud_range?
3 — Factoriser les codes
Si vous avez suivi la partie optionnelle de la session précédente, vous devriez avoir factorisé vos fichiers BFS.py et DFS.py en une classe Traversal dont vous dérivez deux classes BFSTraversal et DFSTraversal.
-
Avec possiblement quelques adaptations dans
Traversal.py, pouvez-vous créer une classeDijkstraTraversalqui hérite deTraversal? Voici le diagramme UML de la session 2, avec cette nouvelle classe :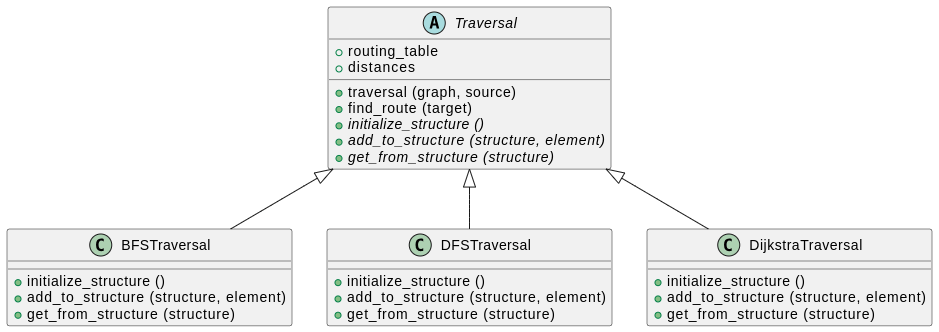
-
Si vous y parvenez, adaptez l’énumération et le constructeur dans
TraversalPlayer.pypour ajouter l’option d’utiliser l’algorithme de Dijkstra.
Pour aller encore plus loin
4 — L’algorithme de Floyd-Warshall
L’algorithme de Dijkstra est ce que l’on appelle un algorithme “1-à-*”. Cela signifie qu’il trouvera les chemins les plus courts depuis une seule position initiale vers toutes les autres positions dans le graphe.
L’algorithme de Floyd-Warshall est ce que l’on appelle un algorithme “*-à-*”. Il calcule simultanément tous les plus courts chemins de tous les sommets vers tous les sommets.
-
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
Correction -
Si vous le souhaitez, vous pouvez essayer d’implémenter cet algorithme (ou peut-être trouver une bibliothèque qui le fait ?).
5 — L’algorithme de Bellman-Ford
L’algorithme de Bellman-Ford est aussi un algorithme “1-à-*”. Cependant, contrairement à l’algorithme de Dijkstra, il a la propriété de pouvoir trouver le chemin le plus court si certaines arêtes ont des poids négatifs. De plus, il peut être utilisé pour détecter un cycle absorbant dans le graphe.
-
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
Correction -
Si vous le souhaitez, vous pouvez essayer d’implémenter cet algorithme (ou peut-être trouver une bibliothèque qui le fait ?).
6 — L’algorithme de Johnson
L’algorithme de Johnson est un algorithme “*-à-*”, qui exploite l’algorithme de Bellman-Ford pour trouver tous les plus courts chemins dans le graphe.
-
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
Correction -
Comment se compare-t-il à l’algorithme de Floyd-Warshall ?
-
Si vous le souhaitez, vous pouvez essayer d’implémenter cet algorithme (ou peut-être trouver une bibliothèque qui le fait ?).