The traveling salesman problem

Bonjour, et bienvenue dans cette leçon sur l’algorithmique et les mathématiques discrètes !

Dans la leçon d’aujourd’hui, vous allez découvrir le problème du voyageur de commerce, qui est probablement l’un des problèmes les plus connus en informatique. Il est aussi souvent utilisé comme premier exemple d’un problème NP-complet, ce qui signifie que nous n’avons pas encore identifié d’algorithme de résolution rapide.

Le problème du voyageur de commerce

Commençons par quelques définitions de base : étant donné un ensemble de villes et le coût de déplacement entre chaque paire de villes, le problème du voyageur de commerce, ou TSP en abrégé, consiste à trouver le moyen le moins cher de visiter toutes les villes et, éventuellement, de revenir au point de départ.

Les problèmes tels que le TSP sont appelés “problèmes d’optimisation”, car l’objectif est de trouver des paramètres qui optimisent une certaine quantité, qui, dans le cas du TSP, est de minimiser le coût total.

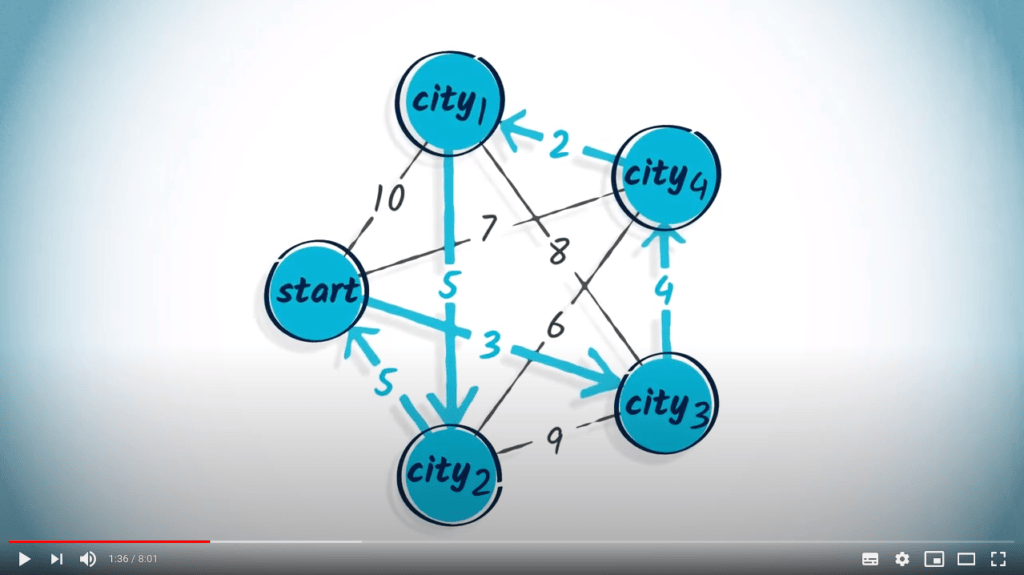
Le TSP peut être représenté par un graphe pondéré, où les sommets représentent les villes, et les poids sur les arêtes représentent le coût de déplacement entre les paires de villes. Résoudre le TSP revient à trouver un chemin passant une et une seule fois par tous les sommets du graphe et ayant un poids total minimal.

Exemple

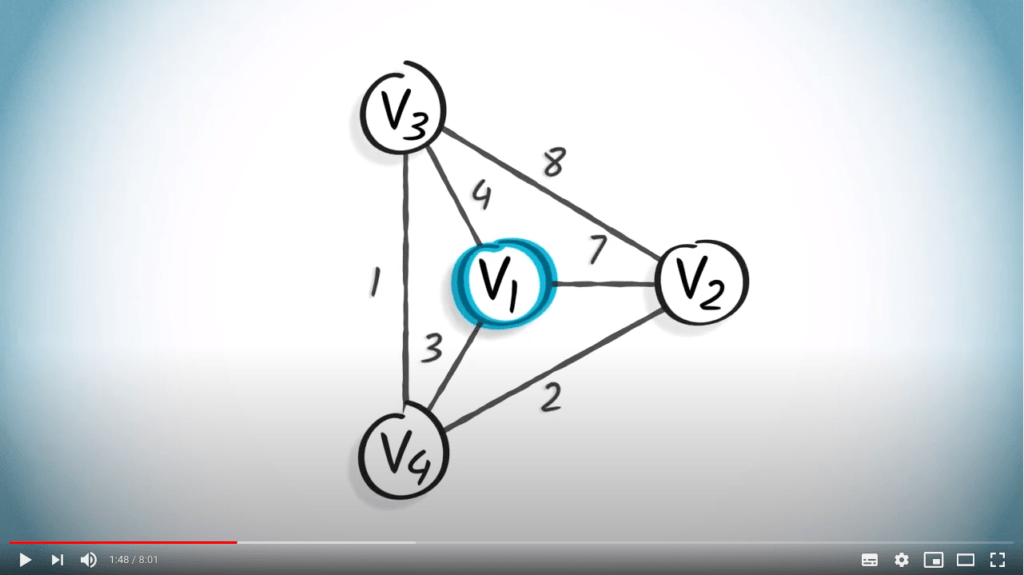
Prenons un exemple. Considérons le graphe suivant, où le point de départ est le sommet $v_1$. Considérons une situation où le voyageur n'a pas à revenir au sommet initial.

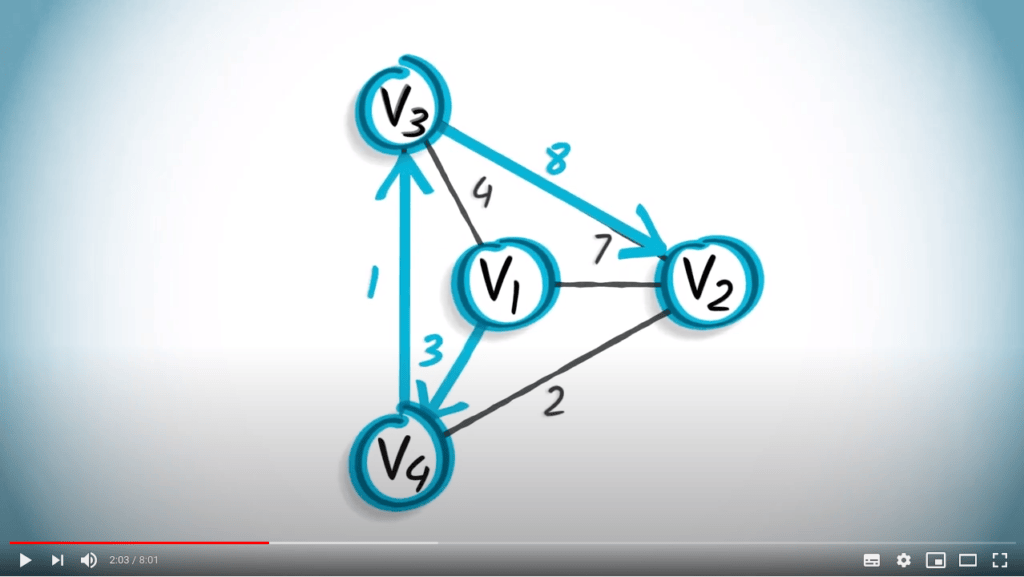
Le chemin $( \{v_1,v_4\}, \{v_3,v_4\}, \{v_2,v_3\} )$ a un poids total de $3 + 1 + 8 = 12$. Ce chemin pourrait potentiellement être une solution du TSP.

Cependant, ce n’est pas une solution optimale, car on peut trouver un chemin avec un poids plus petit.

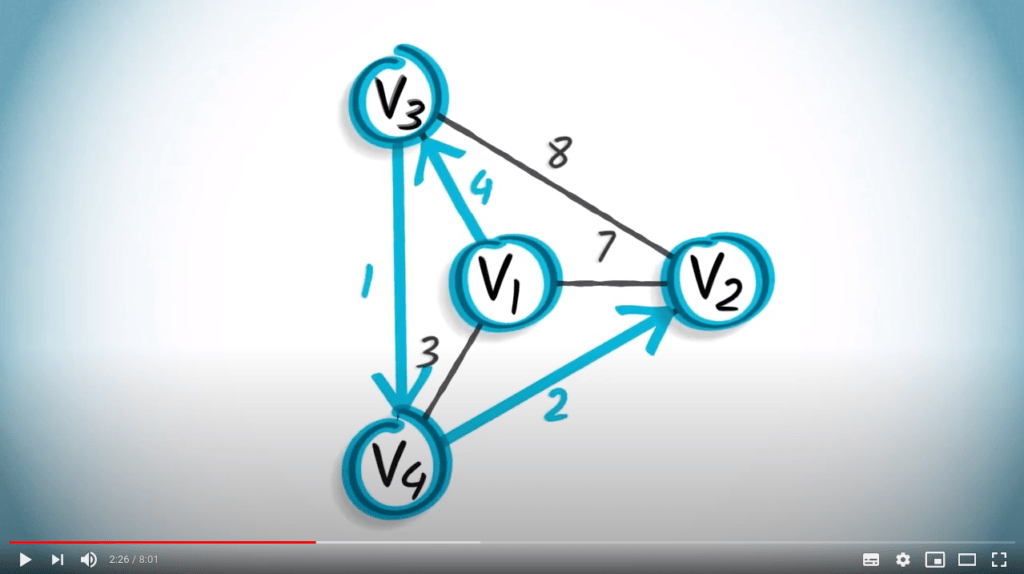
Le chemin $( \{v_1,v_3\}, \{v_3,v_4\}, \{v_2,v_4\}) $ a un poids total de $4 + 1 + 2 = 7$, et est le chemin le plus court partant de $v_1$ et passant par tous les sommets du graphe. C'est donc la solution optimale du TSP pour ce graphe.

Le TSP dans les problèmes quotidiens

Le TSP est un problème récurrent que l’on retrouve dans de nombreux domaines de l’informatique. Voici quelques exemples.

Le TSP apparaît naturellement comme un sous-problème dans de nombreuses applications de transport et de logistique, telles que, par exemple, la planification des itinéraires de bus scolaires et la prise en charge des élèves à différents endroits. D'autres exemples pouvant être modélisés comme des TSP incluent la planification des livraisons de repas aux personnes confinées à domicile et la planification des tournées des camions postaux pour la collecte des colis.

Le TSP intervient également lorsqu'il s'agit de minimiser le temps et les coûts d'un voyage potentiellement long et coûteux. C'est le cas, par exemple, des satellites qui doivent passer par plusieurs emplacements différents pour accomplir leurs missions.

Le déploiement de la fibre optique soulève le problème de desservir un ensemble de lieux tout en limitant les travaux de construction impliqués. Un tel problème peut généralement être formalisé comme un TSP.

La planification d'une machine pour percer des trous dans un objet lors d'un processus de fabrication peut aussi être vue comme un TSP. Les trous à percer sont les "villes", et le coût de déplacement est le temps nécessaire pour déplacer la tête de perçage d'un trou à l'autre.

Le TSP comme réduction pour d’autres problèmes

En informatique, une réduction est une méthode pour transformer un problème en un autre problème, généralement pour lequel des solutions sont déjà connues.

Intuitivement, un problème $P$ est réductible à un problème $Q$ si un algorithme pour résoudre efficacement le problème $Q$ peut aussi être utilisé pour résoudre le problème $P$. D’une certaine manière, cela signifie que lorsque vous résolvez le problème $Q$, une partie de ce que vous faites peut aussi être considérée comme la résolution du problème $P$.

Plus formellement, réduire un problème $P$ à un problème $Q$ se fait en trouvant deux algorithmes polynomiaux $alg_1$ et $alg_2$ tels que, si l’algorithme $alg_Q$ résout le problème $Q$, alors l’algorithme concaténé $ [alg_1, alg_Q, alg_2]$ résout le problème $P$.

Pour mieux comprendre la réduction, pensez à la traduction de langues. Imaginez que vous avez un moyen de résoudre un problème en français, mais que votre problème est exprimé en anglais. Une solution possible est de d'abord traduire votre problème en français, de le résoudre en français, puis de traduire la solution en anglais. C'est un exemple de réduction.

Continuons en anglais. Pas de français, je vous le promets !

La réduction est un moyen très pratique d’obtenir rapidement des résultats. Par exemple, la réduction peut être utilisée pour prouver qu’un problème peut être résolu par un algorithme donné, ou pour montrer qu’un problème est au moins aussi difficile qu’un autre. En d’autres termes, si $P$ est réductible à $Q$, alors vous pouvez résoudre $P$ en utilisant un algorithme conçu pour résoudre $Q$.

Cela ne vous dit rien sur la capacité à résoudre $Q$ en utilisant un algorithme conçu pour résoudre $P$. Donc, on peut seulement dire que $Q$ est au moins aussi difficile que $P$.

Le méta-graphe

Voyons maintenant comment ramasser tous les morceaux de fromage dans un labyrinthe est une réduction du TSP.

Considérons ce labyrinthe, qui montre également son graphe associé.

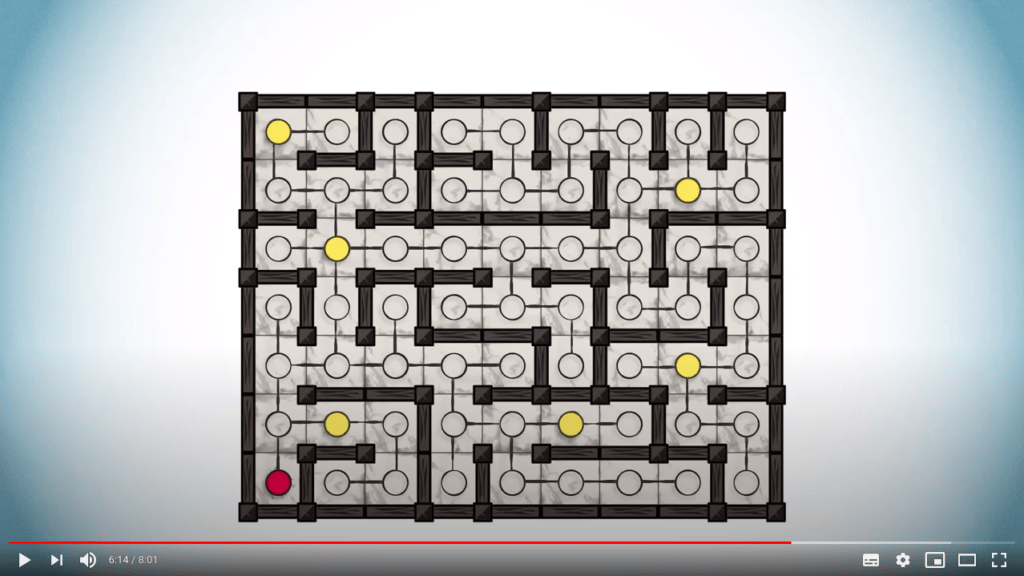
Les morceaux de fromage sont représentés par des sommets jaunes. Notre position de départ est indiquée en rouge.

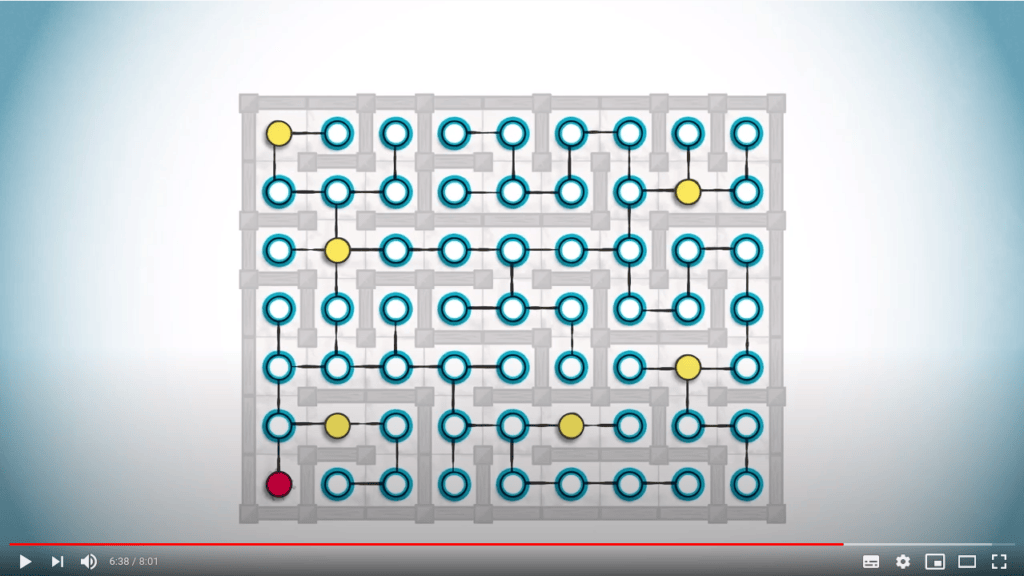
Il est facile de voir comment déterminer le chemin le plus court pour collecter tous les morceaux de fromage revient en quelque sorte à résoudre un TSP. Cependant, si nous utilisons ce graphe pour résoudre le TSP, vous pouvez voir que nous allons passer par de nombreux sommets parasites, qui ne contiennent pas de fromage. Nous aimerions ne passer que par les sommets qui contiennent un morceau de fromage.

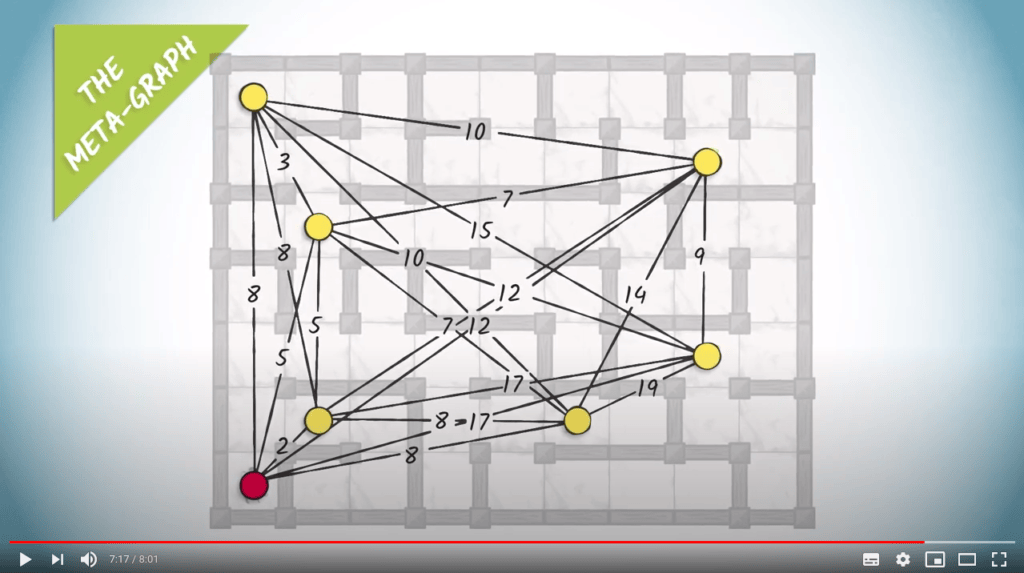
Nous proposons donc de transformer notre graphe en un nouveau graphe, que nous appelons le "méta-graphe". Les sommets du méta-graphe sont la position de départ plus les morceaux de fromage. Le poids entre deux sommets dans le nouveau graphe correspond à la longueur d'un chemin le plus court entre les sommets correspondants dans le labyrinthe. Si nous faisons cela pour chaque paire de sommets colorés dans l'exemple précédent, nous obtenons un graphe complet avec sept sommets. Pour décider comment passer d'un sommet à un autre, un algorithme de routage doit être utilisé.

Nous pouvons maintenant résoudre le problème de trouver la route la plus courte pour attraper tous les morceaux de fromage. D’abord, nous construisons le méta-graphe. Ensuite, nous résolvons le TSP sur le méta-graphe. Puis nous utilisons le routage pour trouver les itinéraires correspondants dans le labyrinthe.

Ainsi, nous avons concaténé trois algorithmes, le premier et le troisième étant polynomiaux, et prouvé que notre problème est réductible au TSP.

Mots de conclusion

Dans la prochaine leçon, nous verrons comment coder une solution au TSP.