Practical activity
Duration2h30Présentation & objectifs
Dans cette activité, vous devrez développer une solution pour récupérer plusieurs morceaux de fromage en un nombre minimum d’actions.
Pour ce faire, nous allons programmer une recherche exhaustive, puis la compléter avec du backtracking.
Si vous souhaitez aller plus loin, nous vous conseillons au moins de jeter un œil à la partie sur les solveurs.
Vous y découvrirez des concepts additionnels intéressants.
Contenu de l’activité
1 — L’algorithme exhaustif
1.1 — Préparez-vous
Avant de commencer, créons d’abord les fichiers nécessaires dans l’espace de travail :
-
pyrat_workspace/players/Exhaustive.py– Dupliquez le fichierTemplatePlayer.py, et renommez-le enExhaustive.py.
Puis, comme dans la session précédente, renommez la classe enExhaustive. -
pyrat_workspace/games/visualize_Exhaustive.ipynb– Créez un fichier qui lancera une partie avec un joueurExhaustive, dans un labyrinthe avec de la boue (argumentmud_percentage), et 5 morceaux de fromage (argumentnb_cheese).
Optionnellement, vous pouvez définir unerandom_seedet unetrace_length.
Vous devriez vous inspirer des autres fichiers dans le sous-répertoiregamesque vous avez rencontrés lors de la session précédente. -
pyrat_workspace/tests/tests_Exhaustive.ipynb– En vous inspirant des fichierstest_DFS.ipynb,test_BFS.ipynbettest_Dijkstra.ipynbvus lors des sessions précédentes, créez un fichiertest_Exhaustive.ipynb.
Ce fichier contiendra les tests unitaires que vous développerez pour tester les méthodes de votre joueurExhaustive.
Dans cette activité pratique, vous aurez besoin d’utiliser un algorithme de parcours à un moment donné.
Si vous n’avez pas réussi à avoir un algorithme de Dijkstra fonctionnel, vous pouvez retirer la boue dans le labyrinthe et utiliser une recherche en largeur (BFS) à la place.
Cela vous permettra de travailler sur l’activité pratique.
Plus tard, vous pourrez essayer de remplacer votre BFS par l’algorithme de Dijkstra pour étendre vos résultats aux graphes pondérés.
1.2 — Programmer l’algorithme exhaustif
Pour écrire un algorithme exhaustif (sans backtracking), suivez les mêmes étapes que la dernière fois, c’est-à-dire :
-
Identifier les méthodes – Vous devez d’abord identifier quelles méthodes vous allez avoir besoin.
N’hésitez pas à revenir sur les articles que vous avez dû étudier pour aujourd’hui.
Une fois identifiées, écrivez leurs prototypes dans votre fichier joueurExhaustive.py. -
Identifier les tests – Déterminez quels tests vous devez effectuer pour garantir que ces méthodes fonctionnent comme attendu.
-
Programmer les méthodes – Ensuite, écrivez du code (tests et joueur) pour vous assurer que vos méthodes fonctionnent comme prévu, et passent les tests que vous avez conçus.
Identifier tous les chemins possibles dans un graphe complet peut se faire de plusieurs manières :
-
Parcours – Dans les articles, nous vous suggérons une approche basée sur un parcours en profondeur (DFS).
C’est encore plus simple avec une implémentation récursive d’un DFS, comparée à celle que vous avez faite dans la session 2.
Cette approche a l’avantage de vous permettre d’intégrer des optimisations à différentes étapes de la recherche. -
Permutations – Chaque chemin dans le graphe complet correspond à une permutation des sommets (et vice versa).
Ainsi, vous pouvez facilement itérer sur toutes les permutations possibles, en utilisant par exemple la bibliothèque Pythonitertools.
Cette solution est plus facile à programmer, mais ne vous permettra pas d’ajouter du backtracking dans votre recherche.
Par conséquent, nous vous suggérons d’utiliser cette approche uniquement si vous avez trop de difficultés avec l’autre.
La vidéo suivante vous montre un exemple de ce que vous devriez observer :
Une fois que vous avez un programme fonctionnel, essayez d’augmenter le nombre de morceaux de fromage.
Quel est le nombre maximum de morceaux de fromage que vous pouvez atteindre dans un temps raisonnable ?
1.3 — Ajouter le backtracking
1.3.1 — Améliorations de la recherche exhaustive
Nous allons maintenant ajouter une stratégie de backtracking à notre recherche exhaustive.
Écrivons deux nouveaux joueurs :
-
Backtracking – Créez un nouveau joueur
Backtracking.py(copiezExhaustive.pycomme base), et un jeu l’utilisant.
Puis, améliorez votre algorithme exhaustif en intégrant une stratégie de backtracking. -
SortedNeighbors – Le nombre de branches explorées par l’algorithme exhaustif dépend de la qualité des premières solutions trouvées.
Pour exploiter cela, créez un nouveau joueurSortedNeighbors.py(copiezBacktracking.pycomme base), et un jeu l’utilisant.
Ensuite, réfléchissez à un ordre dans lequel il serait intéressant d’explorer les sommets, et mettez à jour vos codes pour que votre recherche en tienne compte.
N’oubliez pas les tests !
1.3.2 — Évaluer vos améliorations
Vous avez maintenant trois programmes basés sur une recherche exhaustive.
Il serait intéressant d’évaluer si vos améliorations accélèrent effectivement la résolution du TSP, ou si vos calculs supplémentaires nuisent aux performances.
Pour cela, voici deux choses à faire :
-
Surveiller le temps – Comparez le temps nécessaire aux différents programmes pour résoudre le TSP.
Pour cela, vous pouvez :-
Tracer le temps moyen (sur 100 parties par exemple) nécessaire pour terminer une partie, en fonction du nombre de morceaux de fromage dans le labyrinthe.
-
Pour un nombre fixe de morceaux de fromage, calculer les distributions des temps nécessaires pour chaque programme.
Ensuite, utilisez des tests statistiques adaptés pour évaluer si les distributions sont significativement différentes.
InformationAssurez-vous d’exécuter vos expériences avec un noyau Python qui désactive les asserts, car cela serait comptabilisé dans le temps d’exécution.
Pour cela, voici deux solutions possibles :-
Sans VSCode :
- Convertissez ce notebook
.ipynben fichier.pyavec la commandeipynb-py-convert <this_notebook.ipynb> <created_file.py>(vous devrez peut-être installeripynb-py-convertavecpip). - Lancez le nouveau fichier Python avec
python3 -O <created_file.py>.
- Convertissez ce notebook
-
Avec VSCode :
- Créez un noyau Jupyter avec la commande suivante :
python3 -m ipykernel install --user --name python-o --display-name "Python (no asserts)". - Modifiez le fichier du noyau (dans
~/.local/share/jupyter/kernels/python-o/kernel.jsonou%APPDATA%\jupyter\kernels\python-o\kernel.json) pour ajouter l’option-Odans la listeargv. - Redémarrez VSCode.
- Créez un noyau Jupyter avec la commande suivante :
-
-
Compter les branches – Comparez les branches coupées et restantes dans votre exploration.
Pour cela, vous pouvez :-
Adapter votre code pour compter combien de branches ont été coupées lors de l’exploration.
Un graphique intéressant à produire est le nombre de branches coupées, en fonction de leur profondeur dans l’arbre (c’est-à-dire le nombre de sommets dans le chemin avant la coupure).
En effet, plus vous coupez tôt une branche, moins vous avez de branches complètes à explorer, et donc plus l’algorithme sera rapide. -
Adapter votre code pour compter combien de branches complètes ont été explorées.
Un graphique intéressant à produire est le nombre de branches complètes explorées de longueur au plus $l$, en fonction de la longueur $l$.
Avec ces indicateurs, quelle est la qualité de votre stratégie de tri dans
SortedNeighbors.py? -
Pour aller plus loin
2 — Factoriser les codes
En vous inspirant des sessions précédentes, vous pouvez essayer de factoriser vos différentes recherches exhaustives.
En effet, nous vous avons demandé plusieurs fois de copier le fichier précédent pour l’utiliser comme base.
Cela a probablement pour conséquence que vous avez plusieurs fois la même fonction dans ces fichiers, ce qui est très problématique.
En effet, si vous trouvez une erreur dans une telle fonction maintenant, vous devrez mettre à jour plusieurs endroits dans vos codes.
C’est une surcharge de travail inutile, et vous risquez d’introduire de nouvelles erreurs en le faisant.
Voici deux choses possibles à faire (choisissez votre préférée) :
-
Bibliothèque – Vous pouvez créer un fichier Python externe (par exemple appelé
tsp_utils.py) et y écrire vos fonctions dupliquées.
Puis, mettez à jour vos joueurs pour importer les fonctions dont vous avez besoin depuis ce fichier. -
Classe – Comme proposé dans la session sur les parcours de graphes, vous pouvez ici créer une classe abstraite
TSPSolver(dans un répertoireutils), qui regroupe les méthodes communes à tous les solveurs exhaustifs.
Ensuite, écrivez les classesExhaustiveTSPSolver,BacktrackingTSPSolveretSortedNeighborsTSPSolverqui héritent deTSPSolver.
Enfin, créez un joueurTSPPlayer.pyqui exploite le solveur que vous souhaitez.Voici un petit diagramme UML qui représente une factorisation possible.
Consultez la session 2 pour un guide sur la lecture de ce diagramme.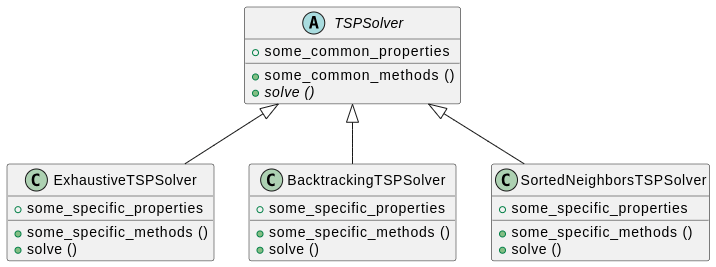
3 — L’algorithme branch-and-bound
Alors que le backtracking est une optimisation basée sur un algorithme DFS, l’algorithme branch-and-bound repose sur une approche de type BFS.
Cet algorithme vous a été présenté dans la section optionnelle d’un article que vous avez dû étudier pour aujourd’hui.
Essayez de l’implémenter dans un nouveau joueur appelé BranchAndBoundTSPSolver.
Comment se compare-t-il à vos autres joueurs ?
Pour aller au-delà
4 — Solveurs
4.1 — Intuition des améliorations possibles
Il peut vous sembler étrange que nous ayons du mal à trouver la solution du TSP dans un graphe avec aussi peu de sommets que 10-15, alors que des outils tels que les GPS, planificateurs de trajets, etc. existent dans la vie réelle.
En pratique, la plupart de ces outils reposent sur ce que l’on appelle des “heuristiques”, qui trouvent des solutions approximatives (pas exactes).
Vous étudierez ces approches lors de la prochaine session.
Cependant, il reste encore de la place pour améliorer les algorithmes exacts.
En effet, on peut facilement imaginer quelques améliorations simples.
Par exemple, il est probablement une mauvaise décision d’aller et venir dans le labyrinthe comme suit :
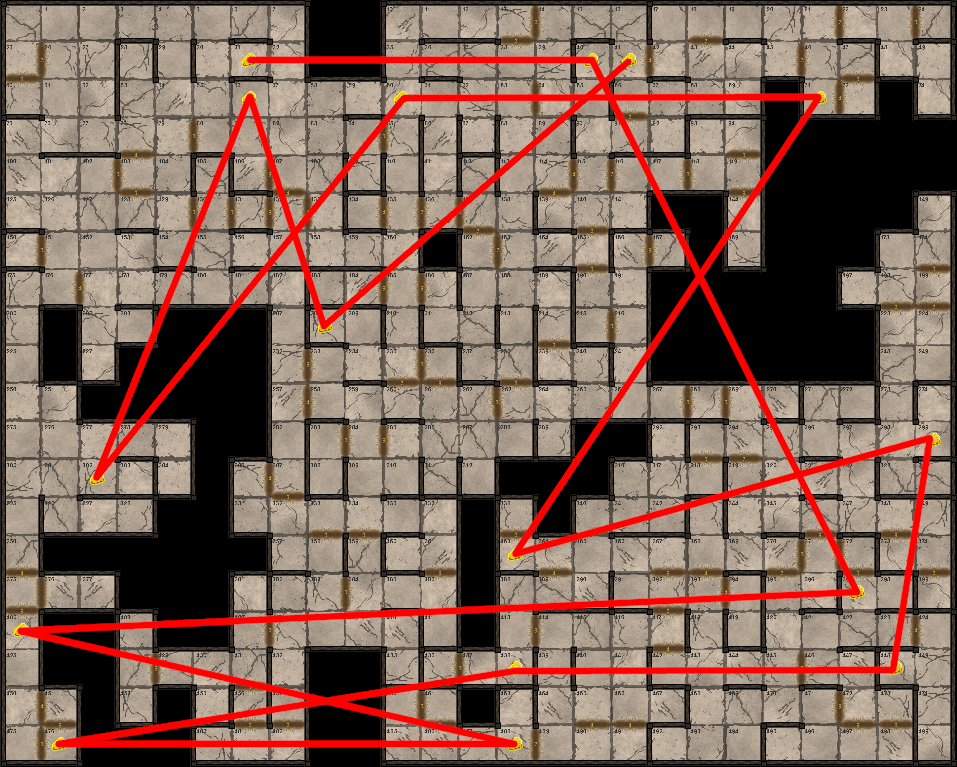
Attraper les morceaux de fromage proches est évidemment mieux que cette approche.
Par exemple, cette permutation est définitivement plus courte (bien que pas nécessairement la meilleure) :
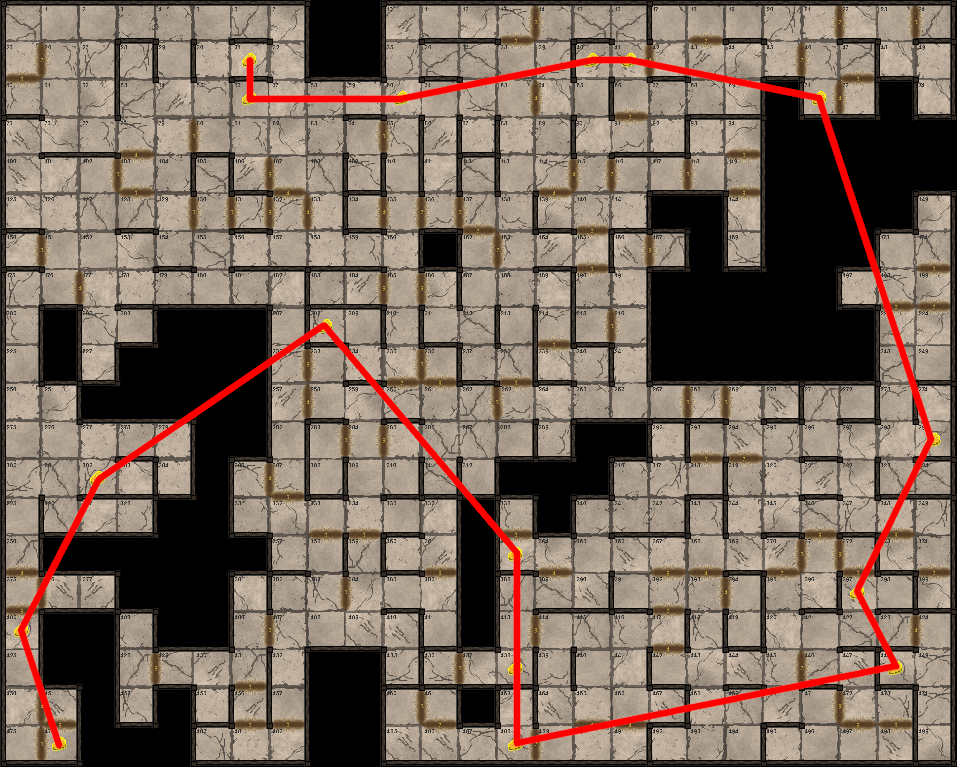
Vous pouvez voir cette optimisation comme une sorte d’inégalité triangulaire.
En effet, le méta-graphe qui représente la répartition des morceaux de fromage dans le labyrinthe est une matrice de distances avec des propriétés particulières.
Cette propriété — et de nombreuses autres — sont exploitées par des outils avancés appelés “solveurs”.
4.2 — Qu’est-ce qu’un solveur ?
Un solveur est un outil générique qui — pour un problème donné — explore l’espace des solutions de manière intelligente.
En effet, les solutions peuvent être organisées dans un espace abstrait, et leur proximité dans cet espace indique la similarité entre les solutions.
Vous pouvez voir cela comme un graphe de solutions, et les solveurs explorent ce graphe intelligemment pour trouver l’optimal.
Nous n’entrerons pas dans les détails du fonctionnement des solveurs, mais voici un lien sur comment le formaliser mathématiquement si vous êtes curieux.
4.3 — Utilisons un solveur
Essayons d’utiliser un solveur pour résoudre le TSP sur un labyrinthe PyRat.
En Python, vous pouvez par exemple utiliser la bibliothèque ORTools.
Pour l’utiliser, vous devez définir une matrice de distances qui modélise votre problème.
Puis, adaptez l’exemple fourni par ORTools pour résoudre le TSP sur un labyrinthe PyRat.
Avec cette solution, vous devriez pouvoir calculer la solution du TSP pour un grand nombre de morceaux de fromage dans un temps de prétraitement raisonnable.