Combinatorial game theory
Reading time15 minEn bref
Résumé de l’article
Dans cet article, nous vous présentons quelques éléments de la “théorie des jeux”.
Cette branche des mathématiques étudie les stratégies, et a de nombreuses applications dans des domaines tels que l’optimisation, la politique ou l’économie.
Points clés
-
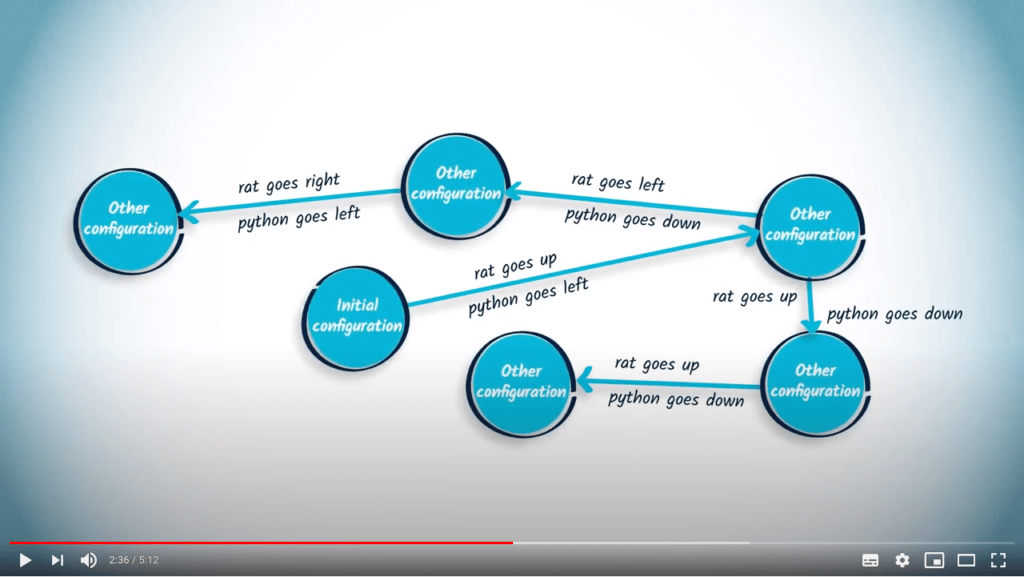
La théorie des jeux représente un jeu dans un espace abstrait de configurations.
-
Une stratégie consiste en une fonction qui explique quelle configuration suivante atteindre, étant donné la configuration actuelle du jeu.
-
Il existe des résultats mathématiques sur les jeux, tels que le théorème de von Neumann.
-
Ces résultats s’appliquent à de nombreux domaines de la vie réelle.
Contenu de l’article
1 — Vidéo
Veuillez regarder la vidéo ci-dessous.
Vous pouvez également lire la transcription si vous préférez.
Pour aller plus loin
2 — Le théorème minimax de von Neumann
2.1 — Catégories de jeux
Il existe plusieurs catégories de jeux, selon que les joueurs jouent simultanément (ex. pierre-papier-ciseaux) ou non (ex. échecs), si les joueurs peuvent cacher certaines informations (ex. poker), etc.
Dans le cas de PyRat, nous considérons un jeu “simultané”.
Cela signifie que les deux joueurs prennent des décisions en même temps.
C’est le cas dans une partie normale de PyRat, car les mouvements sont appliqués à une période fixe.
PyRat est aussi un jeu à “information parfaite”, car toutes les informations sur le plateau, toutes les décisions possibles qui peuvent être prises (et les gains qui en résulteraient), ainsi que l’objectif du jeu, sont connus de tous les joueurs.
De plus, le jeu est “non coopératif”, car chaque joueur essaie de gagner contre l’autre.
En outre, PyRat est un jeu à “somme nulle”, car un morceau de fromage pris par un joueur ne sera pas pris par l’adversaire.
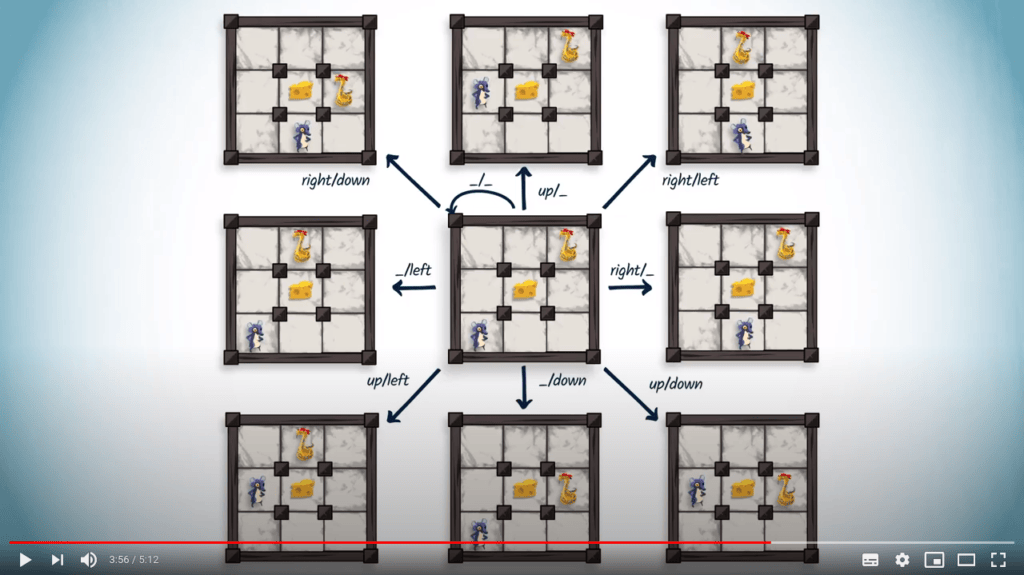
Enfin, PyRat admet un nombre fini de stratégies pures, car le nombre de décisions possibles par sommet de l’arène est un entier.
Une stratégie pure est une définition complète de la façon dont un joueur jouera une partie.
En particulier, elle détermine le coup qu’un joueur fera pour chaque situation qu’il pourrait rencontrer.
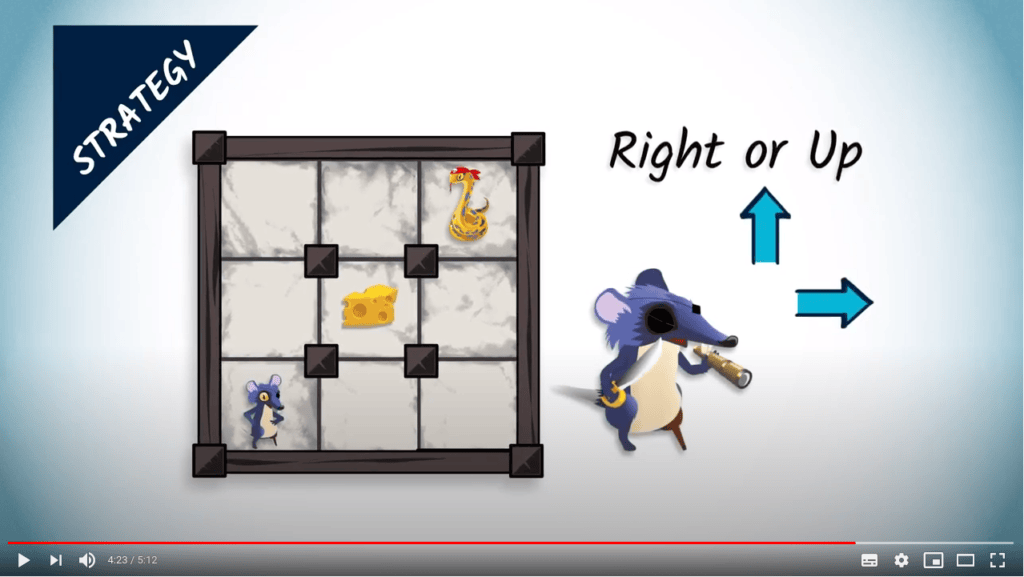
Lorsqu’une stratégie attribue des probabilités à chaque décision, on parle de stratégie mixte.
2.2 — Le théorème
Le théorème minimax de John von Neumann est un résultat important en théorie des jeux.
Dans un jeu non coopératif, simultané, à information parfaite, avec un nombre fini de stratégies pures et à somme nulle, le théorème affirme qu’il existe au moins une situation d’interaction stable, à savoir une situation dans laquelle aucun des deux joueurs n’a intérêt à changer sa stratégie mixte si l’autre ne la change pas.
En d’autres termes, ce que dit le théorème, c’est qu’il existe une situation dans laquelle les deux joueurs devraient se stabiliser, car changer de stratégie n’améliorerait pas les gains tant que l’adversaire ne change pas non plus de stratégie.
Pour aller plus loin
-
Le théorème de von Neumann est un cas particulier d’un équilibre de Nash.
-
Un problème célèbre de la théorie des jeux.