Installing Python modules

En bref

Résumé de l’article

Dans cet article, nous entrons plus en détail sur le gestionnaire de modules Python, pip. Cet outil est central en Python pour installer des modules externes, qui sont des collections de fichiers et de fonctions pour répondre à vos besoins.

Points clés

• Un module est une collection de fonctions et de variables, généralement avec une cohérence thématique.

• En Python, pip permet d’installer simplement des modules.

Contenu de l’article

1 — Packages et modules

En Python, une bibliothèque externe s’appelle un “module”. Un module est un fichier contenant du code (fonctions, variables), que vous pouvez réutiliser dans votre propre code.

Le langage Python est livré avec une pléthore de fonctions déjà définies regroupées en modules thématiques.

Nous allons maintenant apprendre à utiliser les modules Python fournis par la communauté Python, qui doivent être installés avant utilisation. Ils permettent d’accélérer votre temps de développement, en s’appuyant sur le travail déjà réalisé par la communauté.

Avant d’aller plus loin, introduisons le concept de “package” Python. Un package est simplement une collection de modules, qui peut être installée dans son ensemble. Il vous permet également d’utiliser des noms de modules pointés, c’est-à-dire des sous-parties d’un module plus large.

Dans cette leçon, nous allons apprendre à installer et utiliser de tels packages Python.

2 — Installer des packages Python

2.1 — Un exemple simple

Supposons que nous devons multiplier deux matrices. Comme vous pouvez le deviner, c’est un problème récurrent, donc il y a une forte probabilité que des packages Python pour cela existent déjà. Un tel package pour le calcul scientifique est NumPy. Utilisons NumPy pour calculer le résultat d’un produit matriciel.

# Needed imports
import numpy as np

# Define matrices A and B
matrix_a = np.array([1,2,3])
matrix_b = np.array([1,1,-1])

# Compute the matrix product of A and B
product = np.matmul(matrix_a, matrix_b)

# Print the matrix product of A and B
print(product)

Remarquez que nous utilisons la syntaxe suivante pour renommer le package dans notre code :

import package_name as new_name

Cela est généralement fait pour raccourcir un nom de package long, mais cela peut aussi être fait pour désambiguïser entre des packages. Dans notre cas, nous renommons simplement numpy en le plus court np.

Enregistrez le script ci-dessus sous le nom matrix_multiplication.py, et exécutez-le. Si vous n’avez jamais installé numpy auparavant, vous devriez obtenir la sortie suivante :

Traceback (most recent call last):
  File "<stdin>", line 2, in <module>
ModuleNotFoundError: No module named 'numpy'

Ce message d’erreur vous informe que le package numpy est absent. En d’autres termes, NumPy n’est pas installé, donc nous devons l’installer avant de l’utiliser.

python -m pip show numpy

python -m pip show numpy

pip show numpy

pip show numpy

2.2 — Utiliser Pip pour installer des packages

Par défaut, de nombreux modules sont déjà installés : ils constituent la bibliothèque standard Python. Cependant, selon votre domaine (ex. traitement du signal, science des données), les modules standards peuvent ne pas fournir certaines fonctionnalités spécifiques. C’est pourquoi des modules ou packages externes existent, pour fournir des fonctionnalités supplémentaires au développeur.

La manière la plus simple d’installer un package en Python est d’utiliser un “installateur de packages”. L’installateur de packages Python s’appelle pip, un acronyme récursif pour “Pip Installs Packages”. Pip pour Python3 s’appelle pip3.

where python

Get-Command python

which python3

which python3

2.2.1 — Installer Pip

Normalement, cet outil a été installé avec l’interpréteur Python. Vous pouvez vérifier cela en exécutant la commande suivante dans un terminal :

python -m pip --version

python -m pip --version

pip3 --version

pip3 --version

Si pip n’est pas installé, consultez le site officiel Python pour l’installer.

2.2.2 — Installer un package externe avec Pip

Maintenant, vous avez l’outil (pip) pour installer des packages externes, mais où pouvez-vous et pip trouver ces packages ?

Le Python Package Index (PyPI) est un dépôt de logiciels pour le langage de programmation Python. PyPI vous aide à trouver et installer des logiciels développés et partagés par la communauté Python. L’installateur pip utilise le dépôt PyPI pour installer les packages que vous spécifiez comme décrit ici.

En gros, cela consiste à lancer pip en spécifiant le package que vous souhaitez installer (ici le package matplotlib).

python -m pip install matplotlib

python -m pip install matplotlib

pip3 install matplotlib

pip3 install matplotlib

Avant d’installer un package, vérifiez le contenu de la page de description du projet dans le dépôt PyPI car vous pouvez y trouver des informations pertinentes sur le package (fonctionnalités) et sur la manière de faire les choses correctement (ex. versions compatibles de l’interpréteur Python, dépendances spécifiques ou contraintes, bibliothèques externes additionnelles à installer pour obtenir des fonctionnalités supplémentaires).

2.2.3 — Contrôler la version du package

Parfois, pour des raisons de compatibilité, vous pouvez avoir besoin d’installer une version spécifique d’un package. Découvrez les différentes versions d’un package disponibles au téléchargement sur PyPI en utilisant la commande suivante (remplacez <package_name> par le nom du module) :

python -m pip index versions <package_name>

python -m pip index versions <package_name>

pip3 index versions <package_name>

pip3 index versions <package_name>

Ensuite, pour installer une version spécifique d’un package, vous pouvez utiliser la syntaxe suivante (remplacez <version_number> par le numéro de version, ex. 1.2.5) :

python -m pip install <package_name>==<version_number>

python -m pip install <package_name>==<version_number>

pip3 install <package_name>==<version_number>

pip3 install <package_name>==<version_number>

Pour mettre à jour un package avec Pip, utilisez simplement :

python -m pip install --upgrade <package_name>

python -m pip install --upgrade <package_name>

pip3 install --upgrade <package_name>

pip3 install --upgrade <package_name>

Si vous avez plusieurs versions de Python installées simultanément (ex. 3.7, 3.11), la commande pip3 install <package_name> devient ambiguë, car il n’est pas clair pour quelle version de Python l’installation est faite. Pour désambiguïser ce cas, nous pouvons appeler le pip d’une version spécifique de Python en utilisant la même syntaxe que pour Windows, même sous Linux et MacOS. Dans ce cas, vous devez simplement préciser l’exécutable Python que vous souhaitez utiliser (ex. python3.7, python3.11).

2.3 — Retour à l’exemple

Pour revenir à notre exemple de multiplication de matrices, installons numpy :

python -m pip install numpy

python -m pip install numpy

pip3 install numpy

pip3 install numpy

Félicitations ! Vous savez maintenant comment trouver, installer et importer un package Python.

Pour aller plus loin

3 — Quelques packages utiles pour s’amuser

Installons quelques packages qui peuvent vous être utiles. Évidemment, cette liste n’est pas du tout exhaustive. N’hésitez pas à parcourir le dépôt, trouver des packages d’intérêt et peut-être les améliorer plus tard via vos contributions.

• Matplotlib – Visualisation avec Python.

  Exemple

  Voici un script exemple utilisant Matplotlib pour créer un graphique simple :

  ​

  Python Java

  # Needed imports
  import matplotlib.pyplot as plt
  
  # Make a simple plot
  plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
  plt.xlabel("$n$")
  plt.ylabel("$n^2$")
  plt.title("Square of some values")
  plt.show()

  // Needed imports
  import org.jfree.chart.ChartFactory;
  import org.jfree.chart.ChartPanel;
  import org.jfree.chart.JFreeChart;
  import org.jfree.chart.plot.PlotOrientation;
  import org.jfree.data.category.DefaultCategoryDataset;
  import javax.swing.JFrame;
  
  /**
   * To run this code, you need to have Java installed on your computer, then:
   * - Create a file named `Main.java` in a directory of your choice.
   * - Copy this code in the file.
   * - Open a terminal in the directory where the file is located.
   * - Run the command `javac Main.java` to compile the code.
   * - Run the command `java -ea Main` to execute the compiled code.
   * Note: '-ea' is an option to enable assertions in Java.
   */
  public class Main {
  
     /**
      * This is the entry point of your program.
      * It contains the first codes that are going to be executed.
      *
      * @param args Command line arguments received.
      */
     public static void main(String[] args) {
         // Create a dataset
         DefaultCategoryDataset dataset = new DefaultCategoryDataset();
         dataset.addValue(1, "Values", "1");
         dataset.addValue(4, "Values", "2");
         dataset.addValue(9, "Values", "3");
         dataset.addValue(16, "Values", "4");
  
         // Create a chart
         JFreeChart lineChart = ChartFactory.createLineChart(
             "Square of some values", // Title
             "$n$", // X-axis Label
             "$n^2$", // Y-axis Label
             dataset, // Dataset
             PlotOrientation.VERTICAL,
             false, // Include legend
             true,
             false
         );
  
         // Display the chart in a window
         JFrame chartFrame = new JFrame("Line Chart Example");
         ChartPanel chartPanel = new ChartPanel(lineChart);
         chartFrame.setContentPane(chartPanel);
         chartFrame.setSize(800, 600);
         chartFrame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
         chartFrame.setVisible(true);
     }
  
  }

  L’exécution de ce script devrait ouvrir une nouvelle fenêtre contenant le graphique suivant :

  

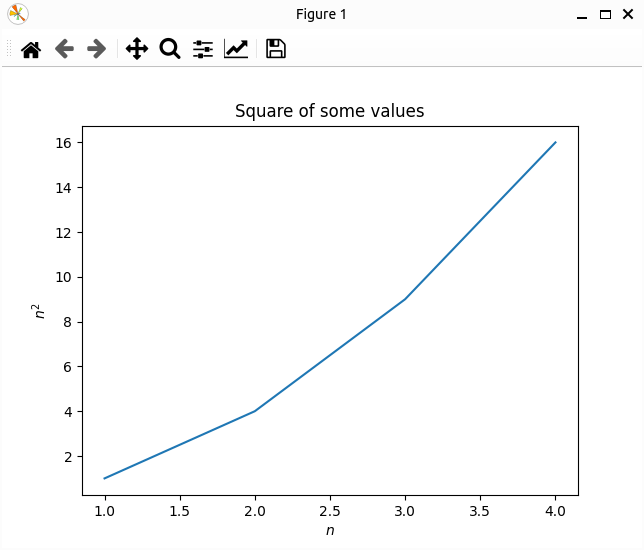
• SciPy – Algorithmes fondamentaux pour le calcul scientifique en Python.

  Exemple

  Voici un script exemple utilisant Scipy pour calculer une telle expression : $​I(a,b)=\int_{0}^{1} ax^2+b , dx$

  ​

  Python Java

  # Needed imports
  from scipy.integrate import quad
  
  # Define function f for which to compute the integral
  def f (x, a: float, b: float):
      return a * x**2 + b
  
  # Compute the integral for some values of a and b
  lower_bound = 0
  upper_bound = 1
  a = 2
  b = 1
  result = quad(f, lower_bound, upper_bound, args=(a, b))
  print(result)

  // Needed imports
  import org.apache.commons.math3.analysis.integration.SimpsonIntegrator;
  import org.apache.commons.math3.analysis.integration.BaseAbstractUnivariateIntegrator;
  import org.apache.commons.math3.analysis.UnivariateFunction;
  
  /**
  * Define function f for which to compute the integral.
  * This class should be put in a file named "FunctionToIntegrate.java"
  */
  public static class FunctionToIntegrate implements UnivariateFunction {
  
      /**
       * Arguments taken by the function.
       */
      private final double a;
      private final double b;
  
      /**
       * Constructor of the class.
       *
       * @param a: First argument of the function.
       * @param b: Second argument of the function.
       */
      public FunctionToIntegrate(double a, double b) {
          this.a = a;
          this.b = b;
      }
  
      /**
       * Function to integrate.
       *
       * @param x: Variable to use for integration.
       * @return   The integral of f.
       */
      public double value(double x) {
          return a * x * x + b;
      }
  
  }
  
  /**
   * To run this code, you need to have Java installed on your computer, then:
   * - Create a file named `Main.java` in a directory of your choice.
   * - Copy this code in the file.
   * - Open a terminal in the directory where the file is located.
   * - Run the command `javac Main.java` to compile the code.
   * - Run the command `java -ea Main` to execute the compiled code.
   * Note: '-ea' is an option to enable assertions in Java.
   */
  public class Main {
  
     /**
     * This is the entry point of your program.
     * It contains the first codes that are going to be executed.
     *
     * @param args Command line arguments received.
     */
     public static void main(String[] args) {
         // Compute the integral for some values of a and b
         double lowerBound = 0;
         double upperBound = 1;
         double a = 2;
         double b = 1;
  
         // Create an instance of the function
         UnivariateFunction function = new FunctionToIntegrate(a, b);
  
         // Use Simpson's rule for integration
         BaseAbstractUnivariateIntegrator integrator = new SimpsonIntegrator();
         double result = integrator.integrate(1000, function, lowerBound, upperBound);
  
         // Print the result
         System.out.println("Integral result: " + result);
     }
  
  }

  L’exécution de ce script devrait produire la sortie suivante :

  Output

  Python Java

  (1.6666666666666667, 1.8503717077085944e-14)

  (1.6666666666666667, 1.8503717077085944E-14)

Pour aller plus loin

• Packaging Python projects.

  Si vous souhaitez savoir comment écrire votre propre package Python, que vous pourrez ensuite distribuer.

• Most downloaded PyPI packages

  Quels sont les packages les plus populaires en Python ?