Bonjour, et bienvenue dans cette leçon sur les structures de file d’attente.
Dans les leçons précédentes, nous avons étudié les deux principaux algorithmes de parcours de graphe, DFS et BFS, et comment construire et utiliser des tables de routage pour naviguer dans leurs graphes correspondants.
Dans cette leçon, nous verrons comment ces algorithmes peuvent être implémentés en pratique, en utilisant des structures de file d’attente.
Une structure de file d’attente est une structure mémoire qui peut être utilisée pour gérer les priorités entre les tâches.

Par exemple, imaginez que nous avons une liste de documents, et que nous devons décider de l'ordre dans lequel nous allons les traiter.
Les structures de file d'attente peuvent être utilisées pour stocker les documents et gérer la priorité entre les documents.
Il n’y a que deux opérations qui peuvent être effectuées lors de l’utilisation d’une structure de file d’attente.
À savoir, ajouter (ou pousser) un élément, et retirer (ou dépiler) un élément.
Je vais maintenant présenter deux structures de file d’attente qui peuvent être utilisées pour gérer les priorités de différentes manières.
Piles / LIFO / Last-In First-Out
Une pile, connue sous le nom de Last-In First-Out, ou LIFO en abrégé, est une structure mémoire pour laquelle le dernier élément ajouté dans la pile est le premier qui sera retiré.

Imaginons une liste de documents que nous devons traiter.
Utiliser un LIFO signifie mettre tous les documents dans une pile.
Vous ne pouvez prendre que le document en haut de la pile, qui a été le dernier ajouté.
Files / FIFO / First-In First-Out
Au contraire, une file, connue sous le nom de First-In First-Out, ou FIFO en abrégé, est une structure mémoire pour laquelle le premier élément ajouté sera le premier à être retiré.

Imaginez cela comme une file d'attente dans un magasin.
Les clients sont servis selon le principe du premier arrivé, premier servi.
Un algorithme unifié pour le parcours de graphe
Une structure de file d’attente peut être utilisée pour gérer les priorités avec lesquelles nous examinons les sommets dans un graphe lors d’un parcours.
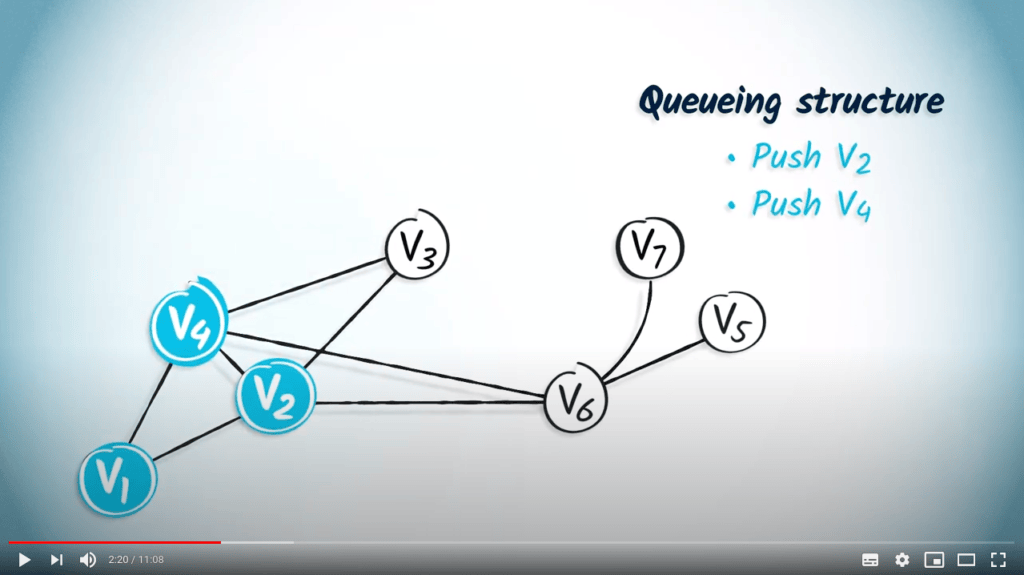
Lors de l'exploration d'un sommet, une structure de file d'attente peut être utilisée pour stocker les sommets voisins, mais seulement si ces sommets n'ont pas été explorés auparavant.
En répétant ce principe jusqu’à ce que la structure de file d’attente soit vide, on obtient un DFS si l’on choisit d’utiliser un LIFO, et un BFS lorsque l’on utilise un FIFO.
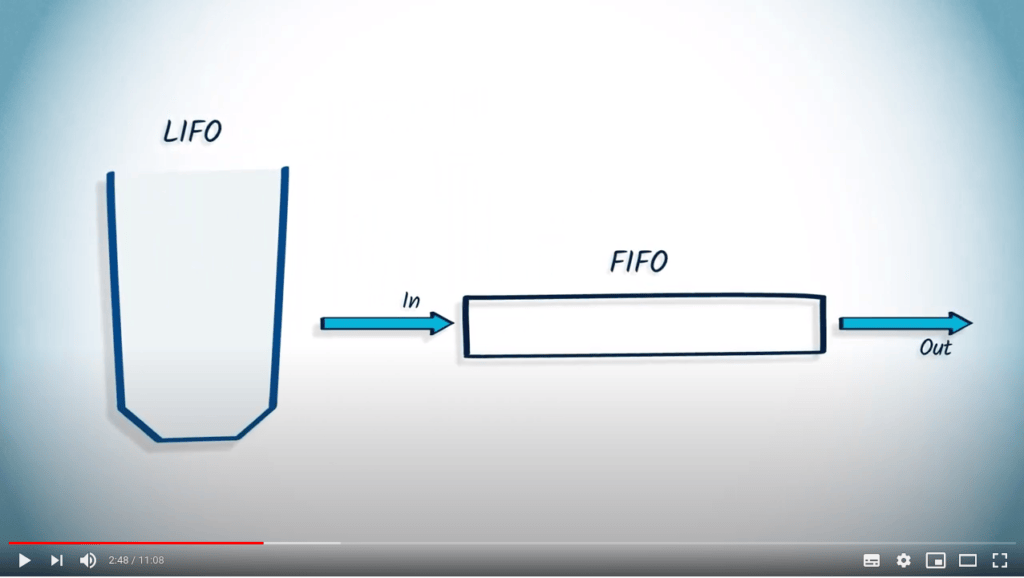
En effet, en utilisant un LIFO, on explore d'abord les derniers sommets qui ont été ajoutés à la structure de file d'attente, et on continue donc à suivre la dernière direction.
Cependant, en utilisant un FIFO, on explore d'abord les premiers sommets ajoutés, et on procède donc par nombre croissant de sauts depuis le départ.
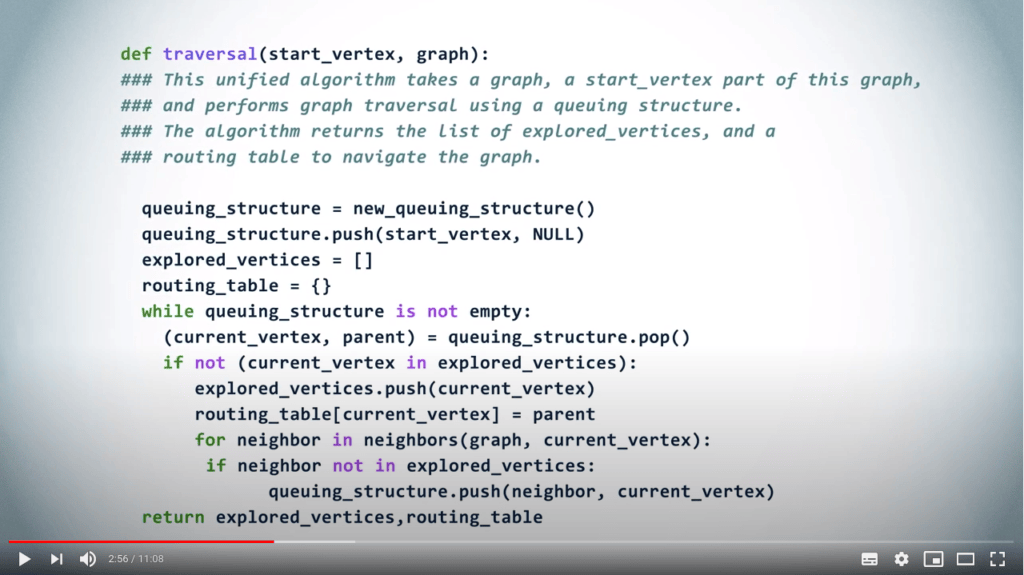
L'algorithme unifié suivant fonctionnera pour un BFS comme pour un DFS en changeant simplement la structure de file d'attente.
En d'autres termes, en utilisant le LIFO pour un DFS, et le FIFO pour un BFS.
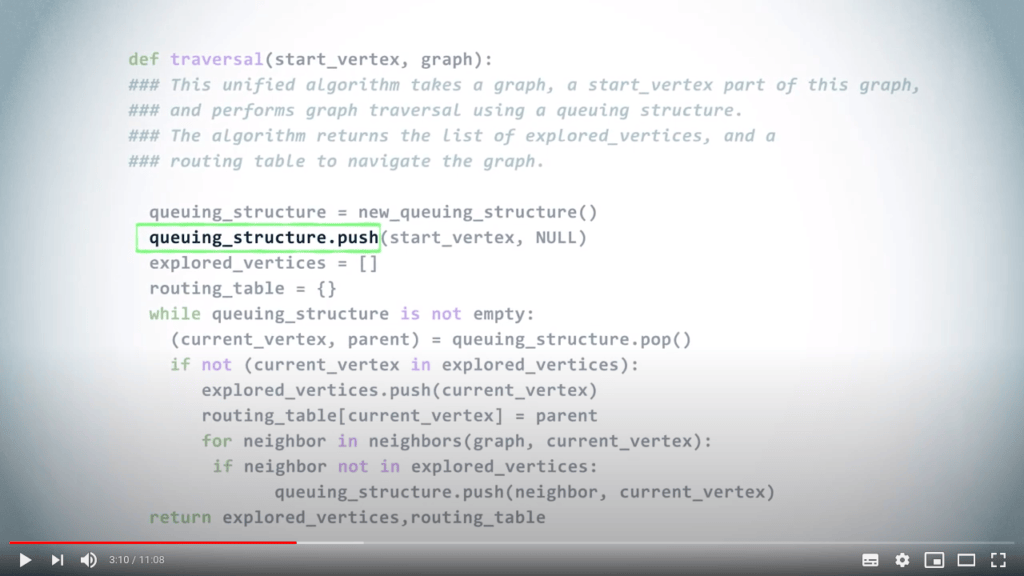
Une fois que nous avons choisi une structure de file d'attente, nous poussons d'abord le sommet de départ.
Ici, nous sommes également intéressés par la construction de la table de routage, donc, dans la structure de file d'attente, nous poussons des couples composés du sommet et de son parent dans l'arbre couvrant correspondant.
Comme le sommet de départ n'a pas de parent, nous utilisons NULL ici.
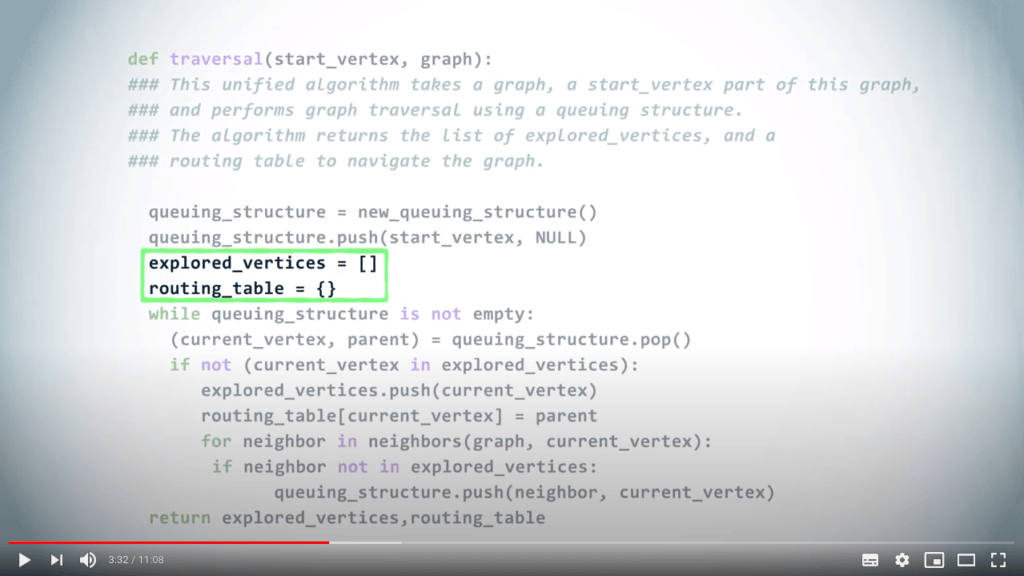
Nous créons également l'ensemble initialement vide des sommets explorés, et la table de routage initialement vide.
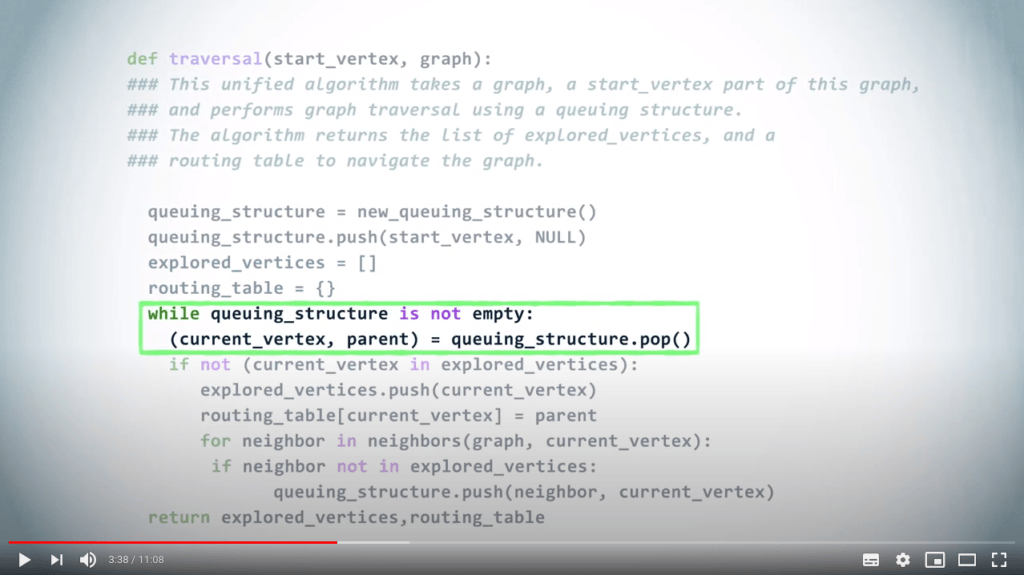
Ensuite, tant que la structure de file d'attente n'est pas vide, nous dépilons un sommet et son parent.
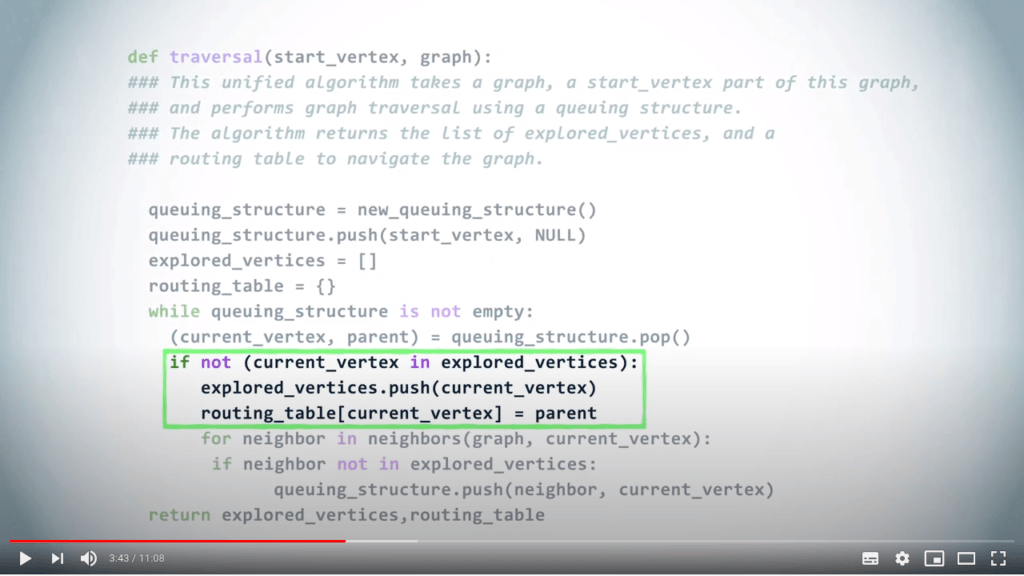
Si ce sommet n'est pas déjà exploré, nous le marquons comme exploré et nous mettons à jour la table de routage en associant le sommet à son parent.
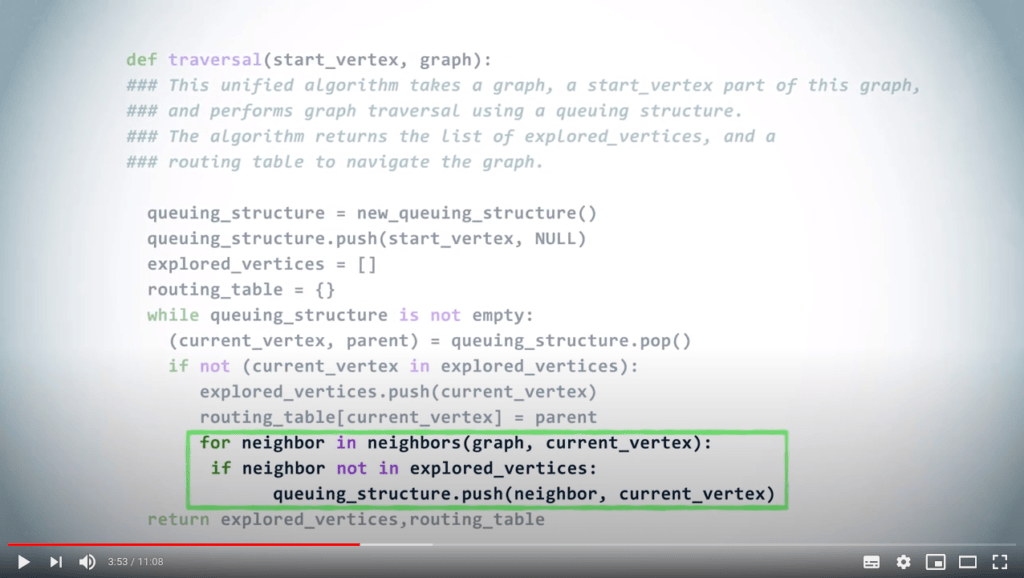
Enfin, nous ajoutons tous les voisins non explorés du sommet à la structure de file d'attente, avec le sommet actuel comme parent.
Si le sommet que nous avons dépilé de la structure de file d'attente était déjà exploré, nous l'ignorons simplement.
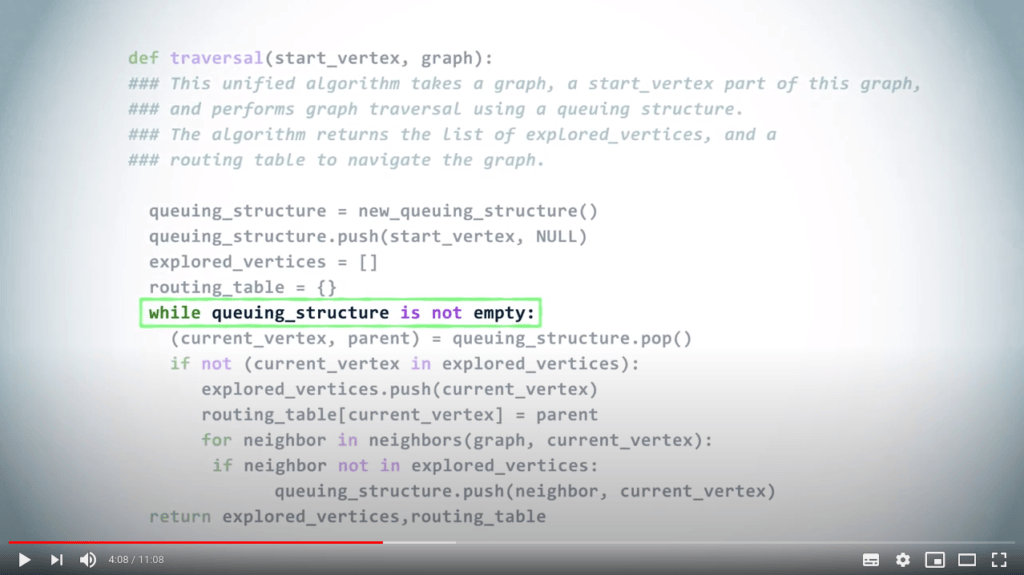
L'algorithme se termine lorsque la structure de file d'attente est finalement vide.
Selon le choix de la structure de file d'attente : un LIFO ou un FIFO, on obtient un DFS ou un BFS.
Illustrons cela avec un exemple.
Application avec DFS
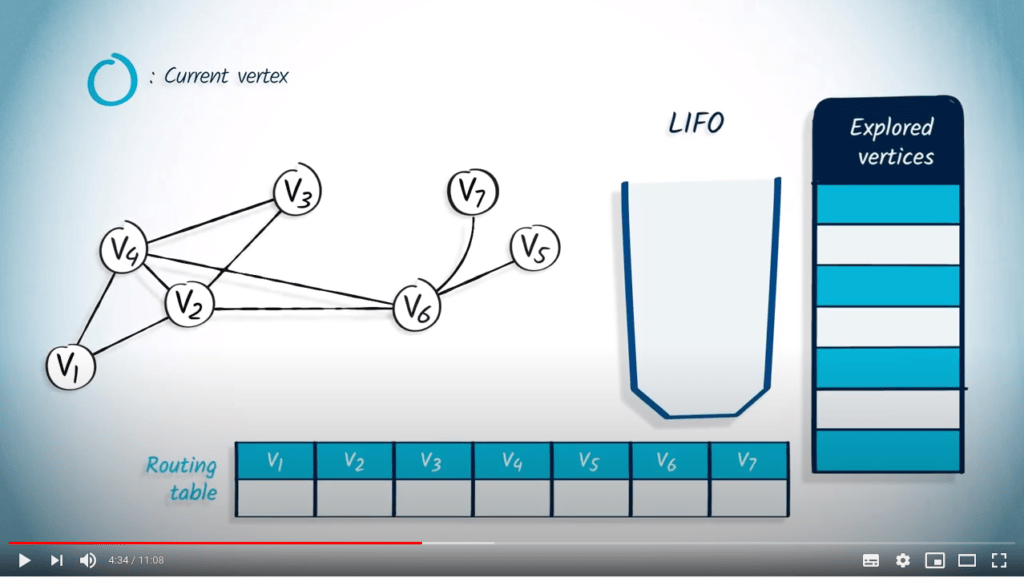
Effectuons un DFS à partir de $v_1$.
Nous montrons le contenu du LIFO au fur et à mesure du parcours du graphe.
La liste des sommets explorés est à droite.
Nous montrons également la table de routage.
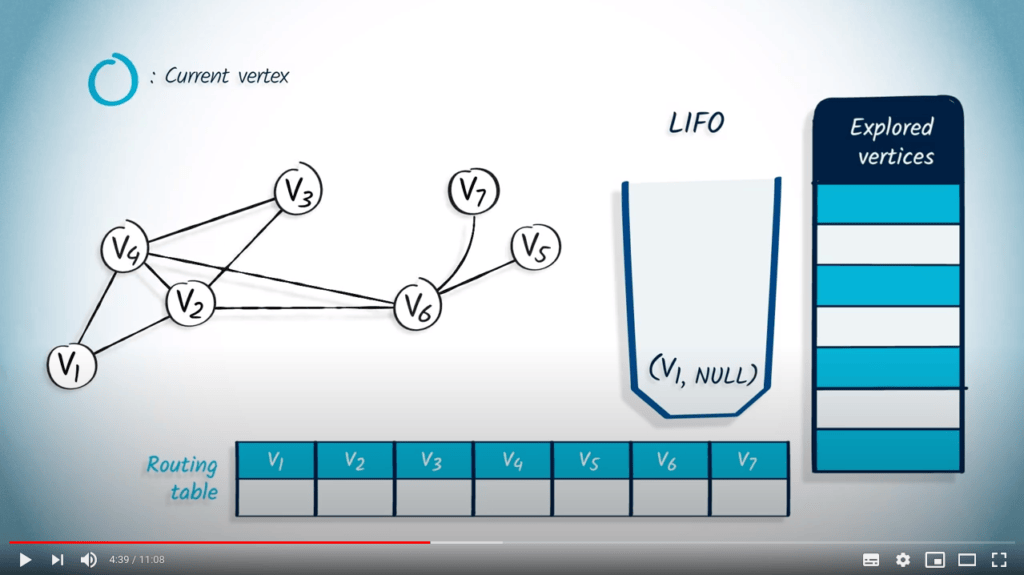
Nous commençons par pousser le sommet de départ $v_1$ dans le LIFO, avec NULL comme parent.
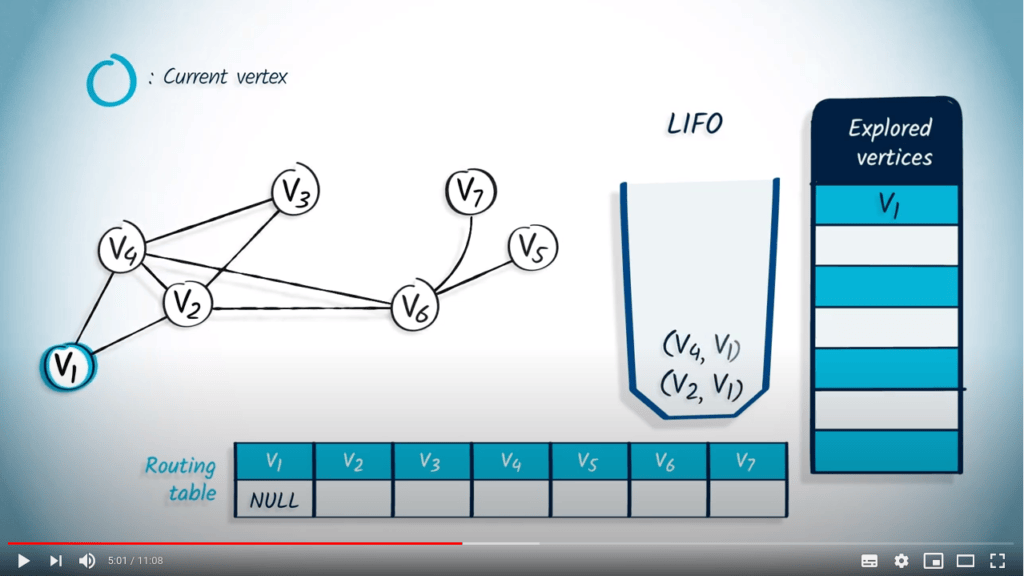
Nous dépilons un sommet et son parent du LIFO, $v_1$, et NULL.
Comme $v_1$ n'est pas dans la liste des sommets explorés, nous le marquons comme exploré et mettons à jour l'entrée correspondant à $v_1$ dans la table de routage en la mettant à NULL.
Ensuite, nous poussons dans le LIFO tous les voisins de $v_1$ qui ne sont pas dans la liste des sommets explorés, à savoir $v_2$ et $v_4$, avec leur parent $v_1$.
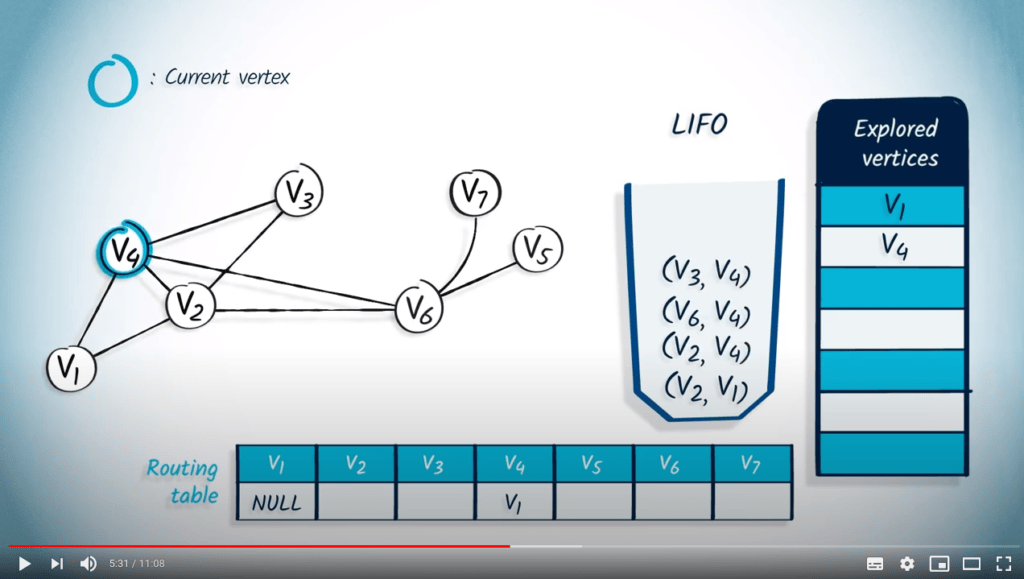
Nous retirons un élément du LIFO, qui est $v_4$, avec $v_1$ comme parent, car c'est le dernier élément qui a été ajouté.
Le sommet $v_4$ n'est pas dans la liste des sommets explorés, donc nous le marquons comme exploré, et mettons à jour l'entrée correspondant à $v_4$ dans la table de routage en la mettant à $v_1$.
Ensuite, nous poussons tous ses voisins non explorés dans le LIFO.
Comme $v_1$ a déjà été exploré, nous poussons $v_2$, $v_6$ puis $v_3$ dans le LIFO, avec $v_4$ comme parent.
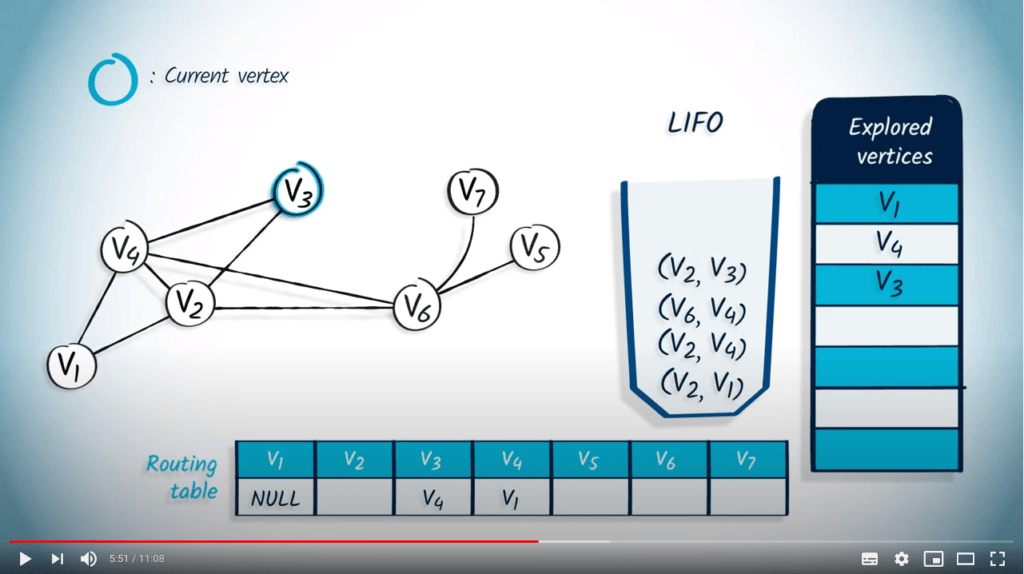
L'élément suivant à retirer est $v_3$ et son parent $v_4$.
Comme $v_3$ n'avait pas été exploré auparavant, nous l'ajoutons à la liste des sommets explorés et mettons à jour la table de routage en conséquence.
Parmi les voisins de $v_3$, seul $v_2$ n'a pas été exploré, donc nous poussons $v_2$ dans le LIFO, avec $v_3$ comme parent.
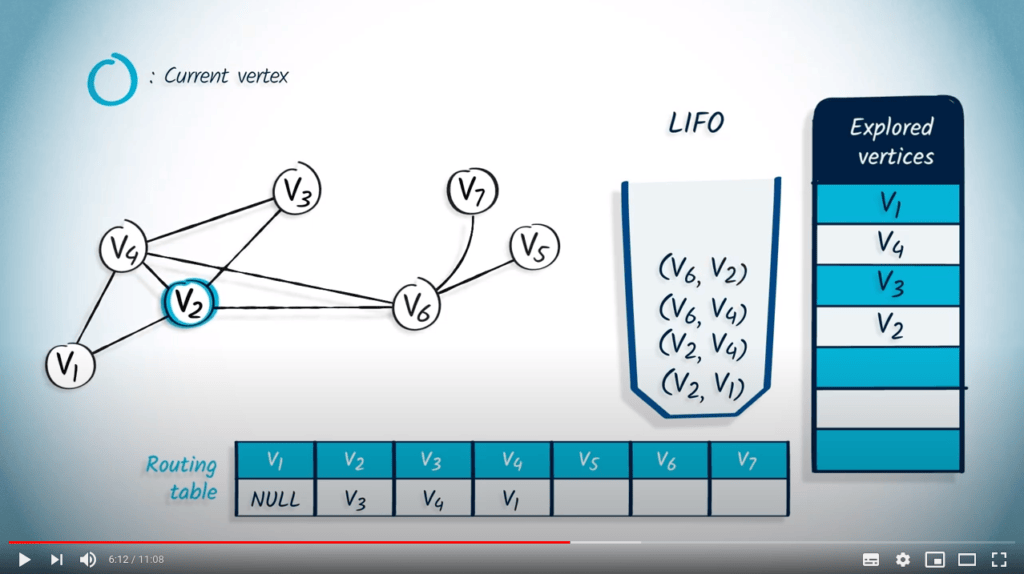
Nous retirons $v_2$ et son parent $v_3$ du LIFO.
Le sommet $v_2$ n'avait pas été exploré auparavant, donc nous le marquons comme exploré et mettons à jour la table de routage en mettant l'entrée correspondante à $v_3$.
Parmi les voisins de $v_2$, seul $v_6$ n'a pas été exploré, donc nous poussons $v_6$ avec $v_2$ comme parent dans le LIFO.
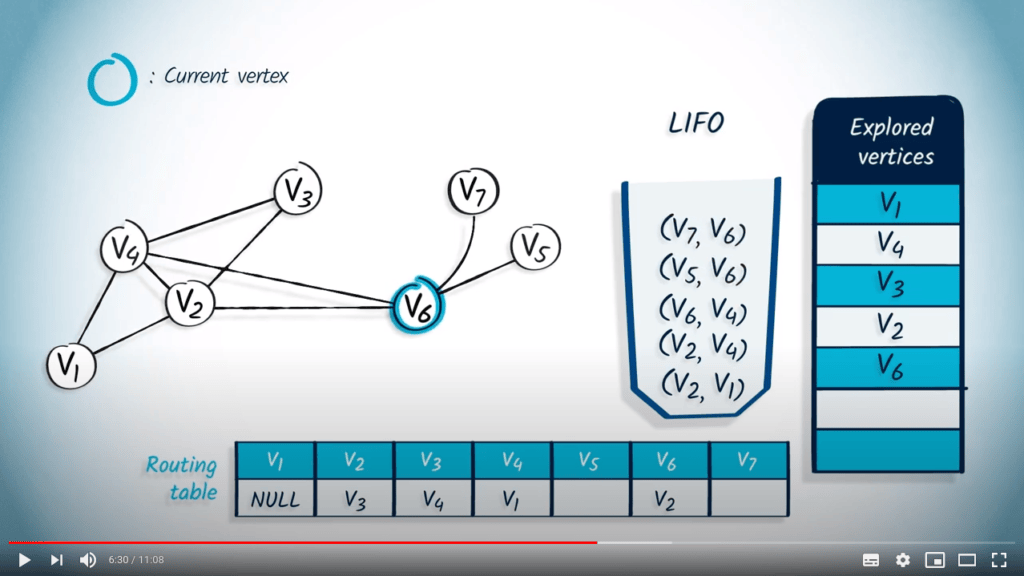
L'élément suivant à retirer est $v_6$ et son parent $v_2$.
Le sommet $v_6$ n'avait pas été exploré auparavant, donc nous le marquons et mettons à jour la table de routage.
Les voisins non explorés de $v_6$ sont $v_5$ et $v_7$, donc nous les poussons dans le LIFO avec $v_6$ comme parent.
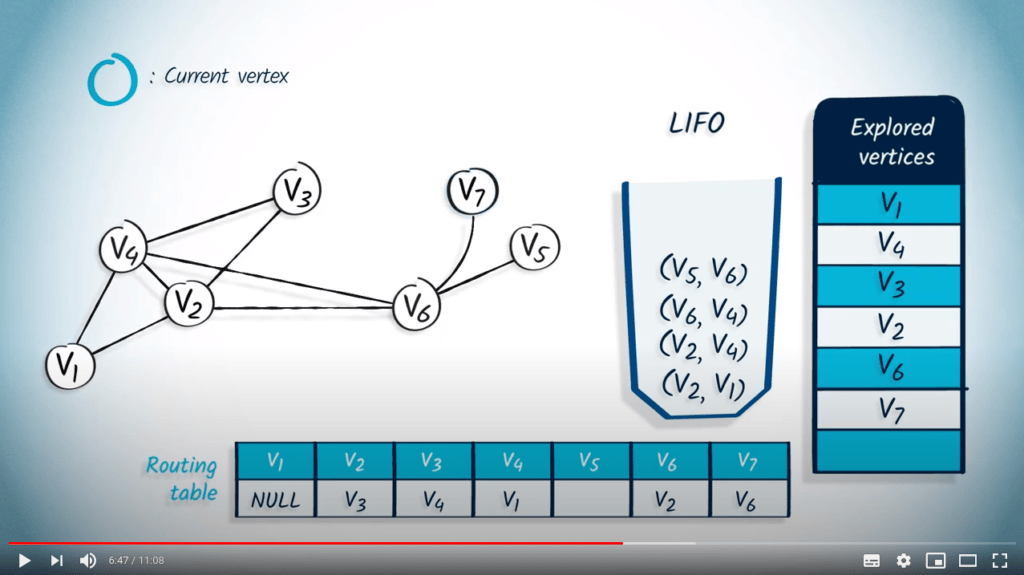
Nous retirons ensuite $v_7$ avec son parent $v_6$.
Comme $v_7$ n'avait pas été exploré auparavant, nous le marquons comme exploré et mettons à jour la table de routage.
Le seul voisin de $v_7$ est $v_6$, qui a été exploré auparavant, donc rien n'est poussé dans le LIFO.
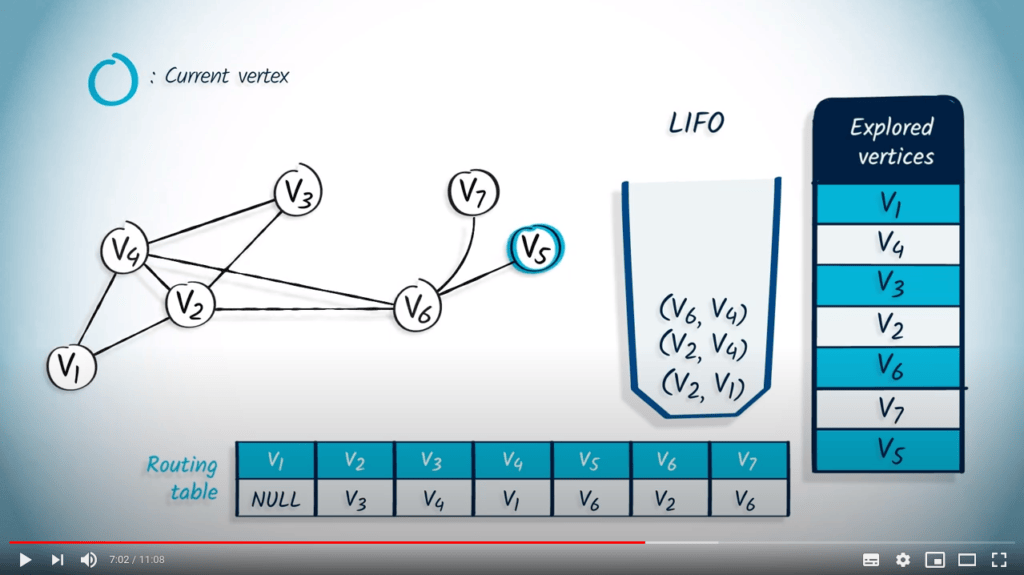
L'élément suivant qui est dépilé du LIFO est $v_5$ et son parent $v_6$.
Le sommet $v_5$ n'avait pas été exploré, donc nous le marquons comme exploré et mettons à jour la table de routage. Ici encore, le seul voisin de $v_5$ est $v_6$, qui a déjà été exploré, donc rien n'est poussé dans le LIFO.
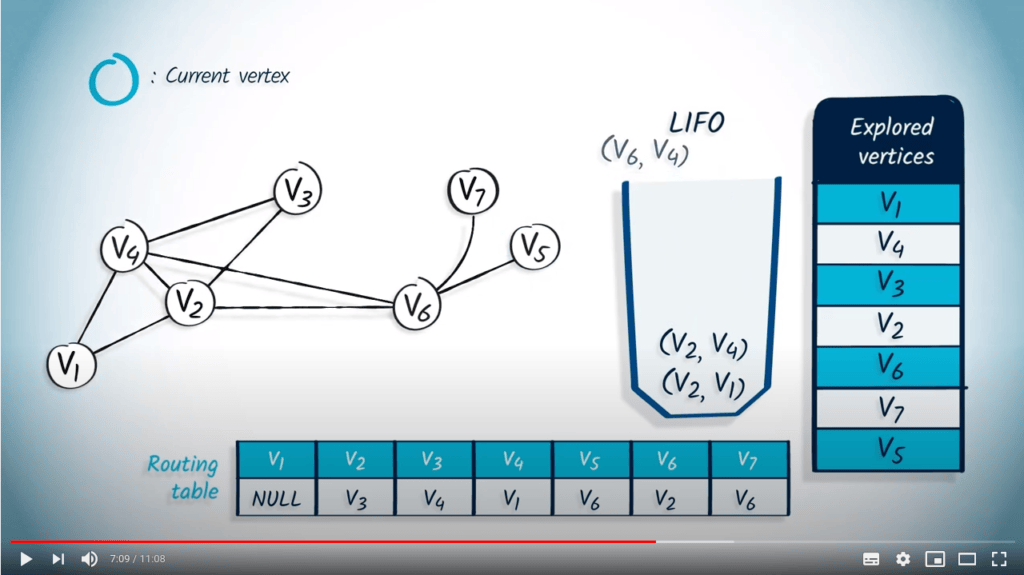
Ensuite, nous dépilons $v_6$ avec $v_4$ comme parent.
Comme $v_6$ a déjà été exploré, rien ne se passe.
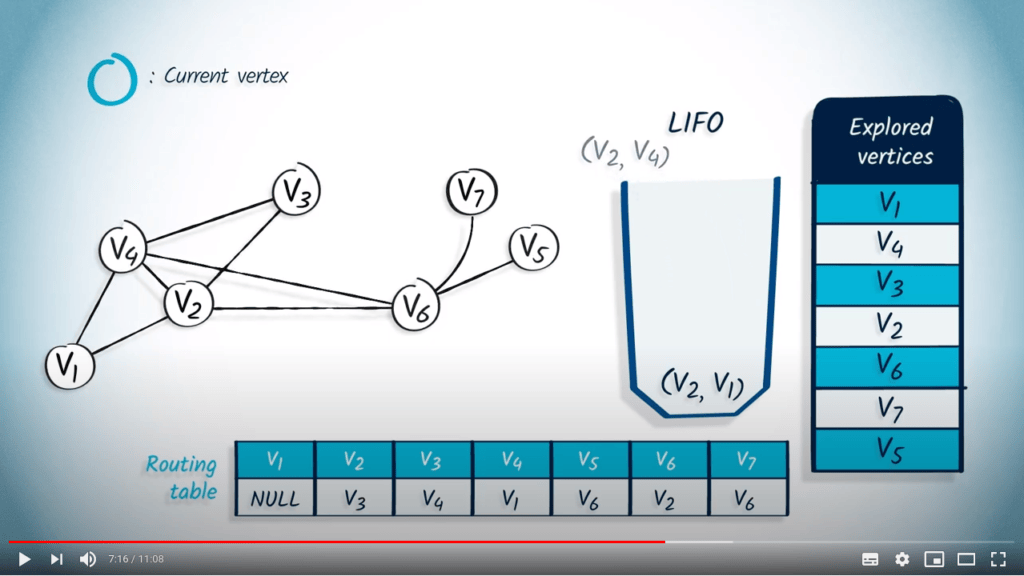
Nous dépilons $v_2$ avec $v_4$ comme parent, et ici encore, $v_2$ a déjà été exploré, donc rien ne se passe.
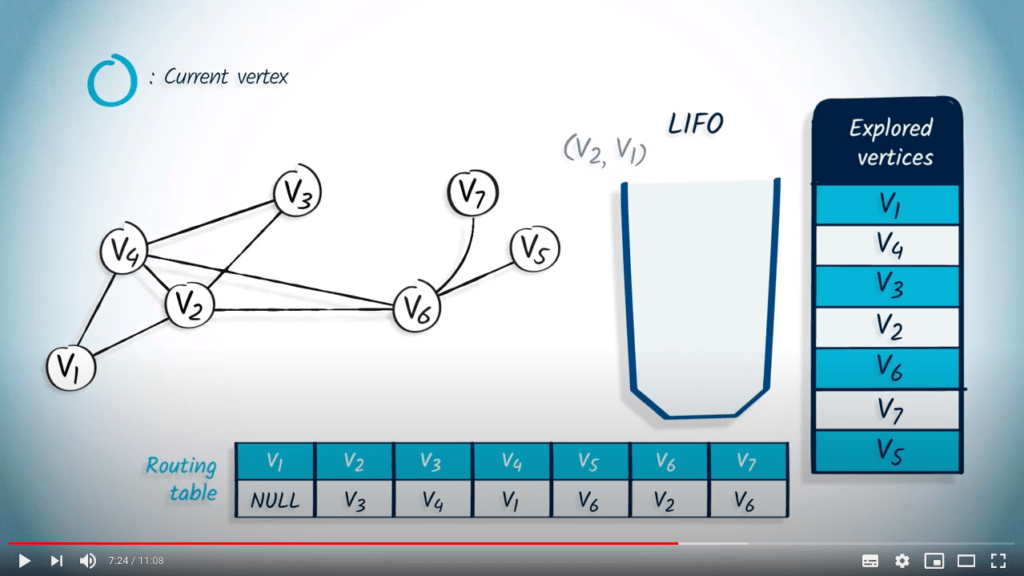
Enfin, $v_2$ avec $v_1$ comme parent est dépilé du LIFO, mais encore une fois, $v_2$ a déjà été exploré, donc rien ne se passe.
La structure de file d’attente est maintenant vide, donc l’algorithme se termine.
Notez que le fait d’utiliser un LIFO correspond directement au fait que nous continuons à explorer le graphe jusqu’à ce que la recherche atteigne un sommet sans voisins non explorés, auquel cas nous revenons aux sommets explorés précédemment.
Application avec BFS
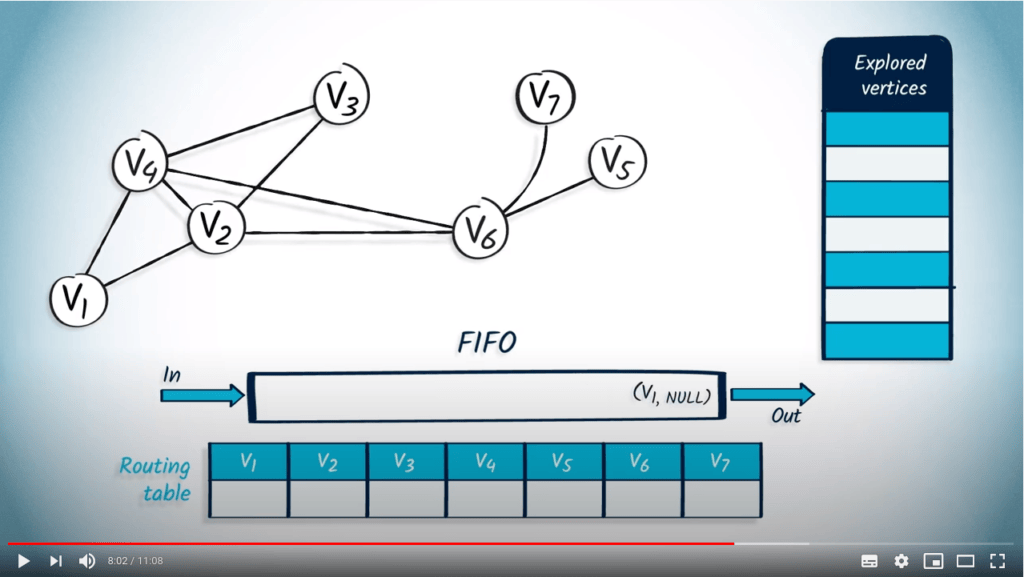
Voyons maintenant comment effectuer un BFS à partir de $v_1$ en utilisant un FIFO.
Nous commençons par pousser $v_1$ dans le FIFO, avec NULL comme parent.
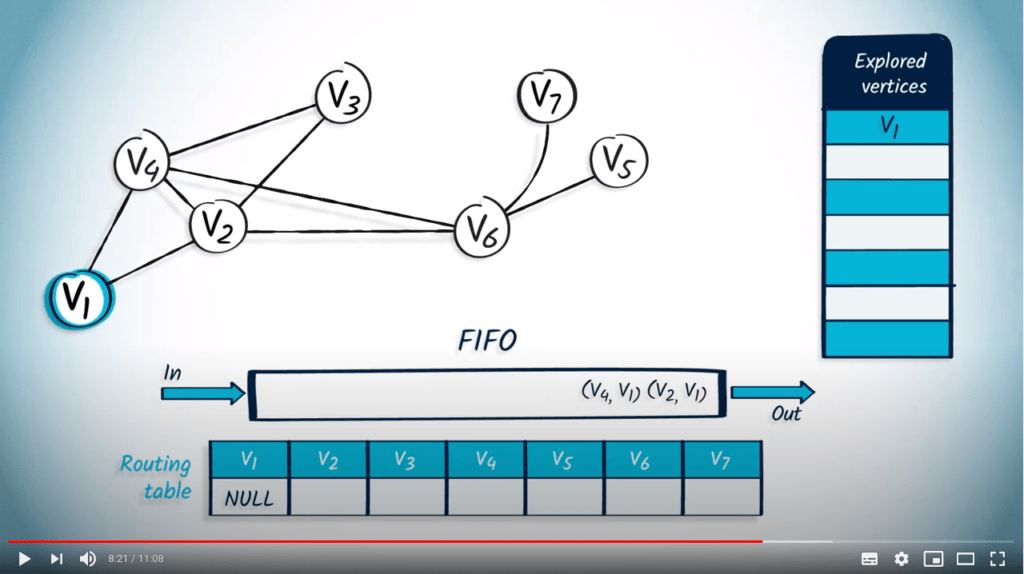
Nous dépilons un sommet et son parent du FIFO, $v_1$ et NULL.
Le sommet $v_1$ n'avait pas été exploré auparavant, donc nous le marquons, et mettons à jour la table de routage.
Ensuite, nous poussons dans le FIFO tous les voisins non explorés de $v_1$, à savoir $v_2$ et $v_4$, avec leur parent $v_1$.
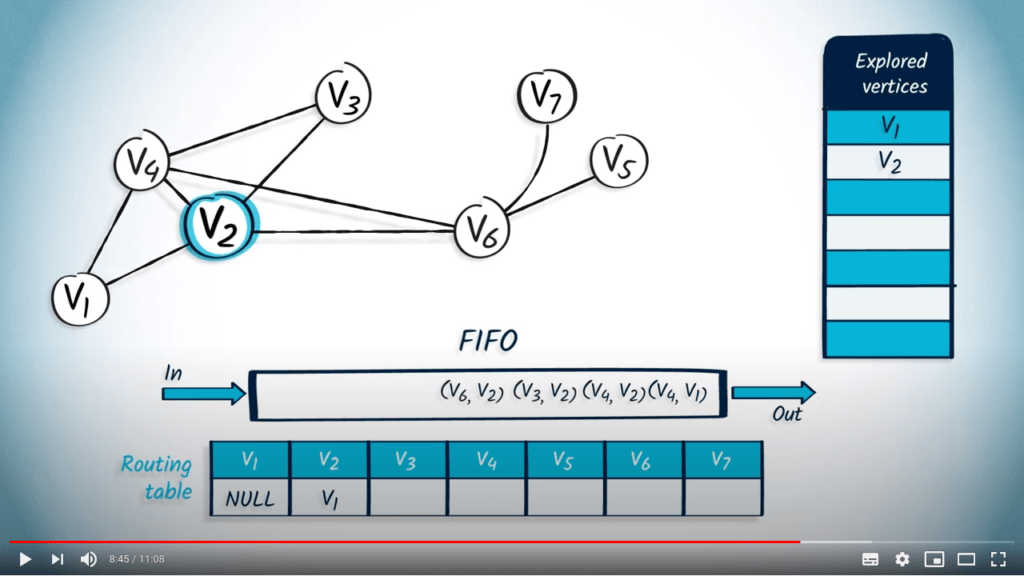
Nous dépilons un élément du FIFO, qui est $v_2$ avec $v_1$ comme parent, car c'est le premier élément qui a été poussé.
Le sommet $v_2$ n'avait pas été exploré auparavant, donc nous l'ajoutons à la liste des sommets explorés et mettons à jour la table de routage en conséquence.
Nous poussons tous les voisins de $v_2$ qui ne sont pas dans la liste des sommets explorés : $v_4$, $v_3$ et $v_6$, avec $v_2$ comme parent.
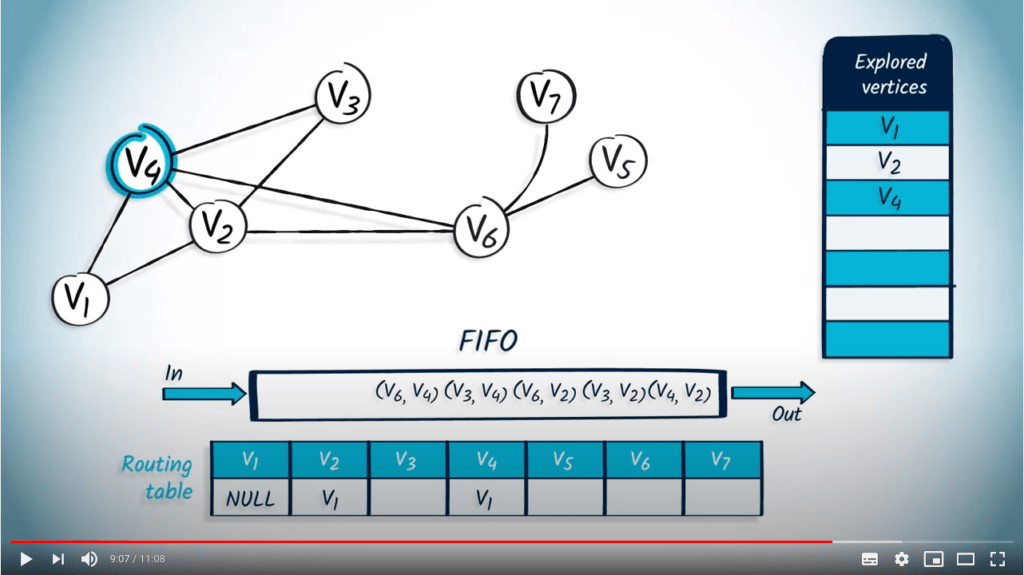
L'élément suivant à retirer du FIFO est $v_4$ avec $v_1$ comme parent.
Comme $v_4$ n'est pas dans la liste des sommets explorés, nous le marquons et mettons à jour la table de routage.
Parmi les voisins de $v_4$, seuls $v_3$ et $v_6$ ne sont pas dans la liste des sommets explorés, donc nous les poussons dans le FIFO avec $v_4$ comme parent.
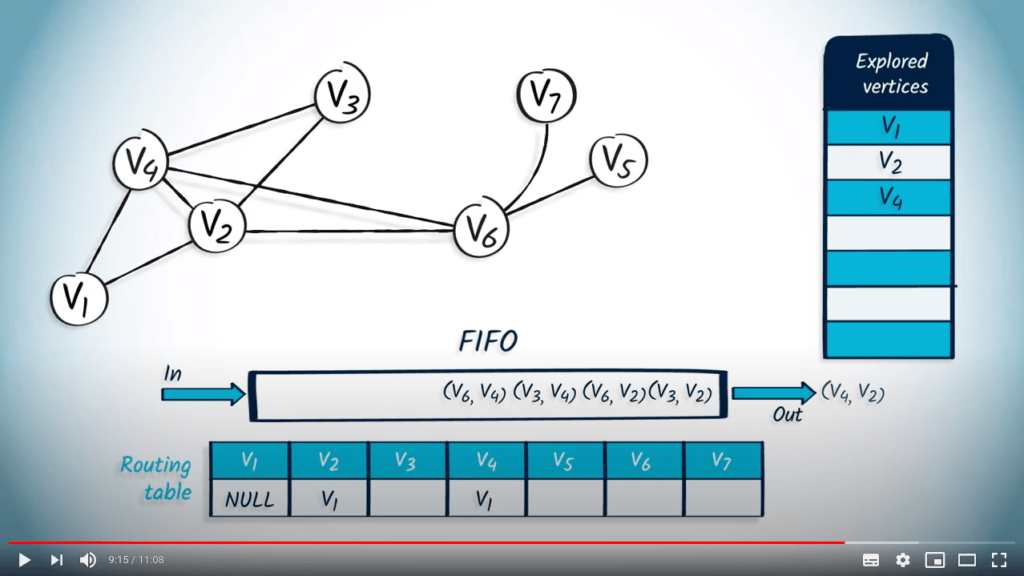
Ensuite, nous dépilons l'élément $v_4$ avec $v_2$ comme parent.
Le sommet $v_4$ a déjà été exploré, donc nous passons au suivant.
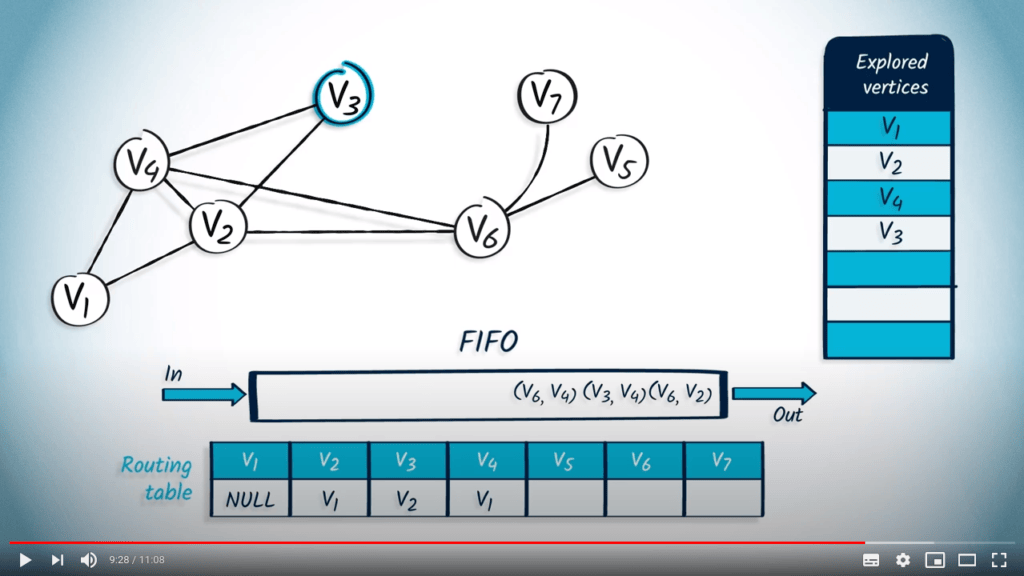
Nous dépilons l'élément suivant du FIFO, $v_3$ avec $v_2$ comme parent.
Le sommet $v_3$ n'avait pas été exploré, donc nous le marquons et mettons à jour la table de routage en conséquence.
Tous les voisins de $v_3$ ont été explorés, donc nous continuons.
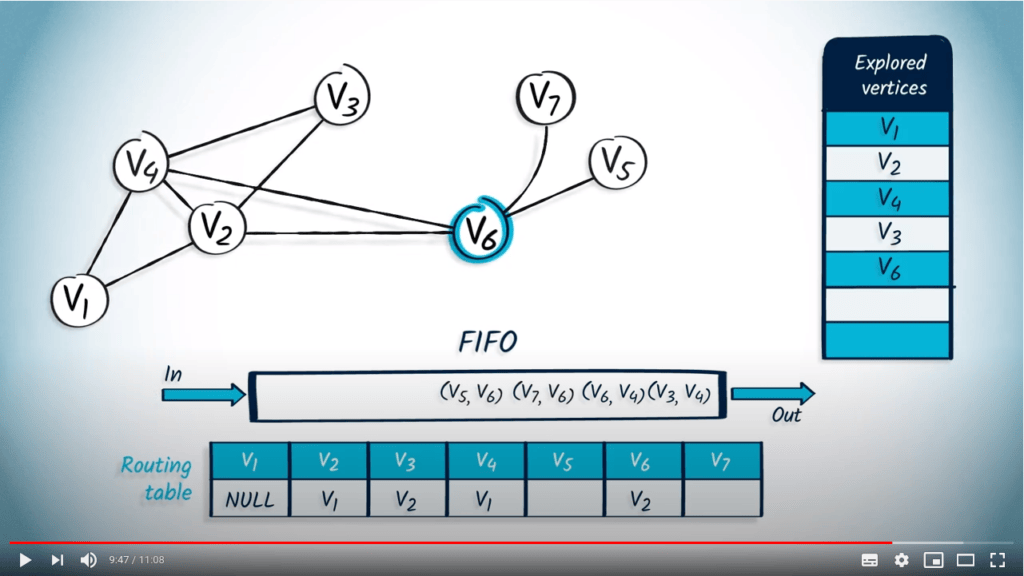
L'élément suivant à dépiler du FIFO est $v_6$ avec $v_2$ comme parent.
Ce sommet n'avait pas été exploré auparavant, donc nous le marquons et mettons à jour la table de routage.
Parmi les voisins de $v_6$, seuls deux voisins sont non explorés : $v_7$ et $v_5$, donc nous les poussons dans le FIFO avec $v_6$ comme parent.
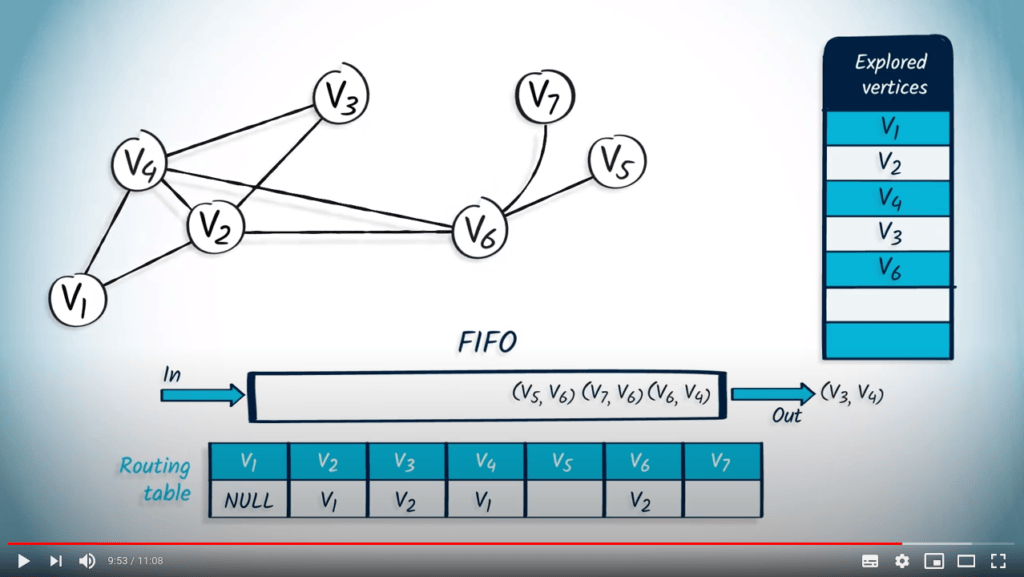
Nous dépilons l'élément $v_3$ avec $v_4$ comme parent, mais comme $v_3$ a déjà été exploré, rien ne se passe.
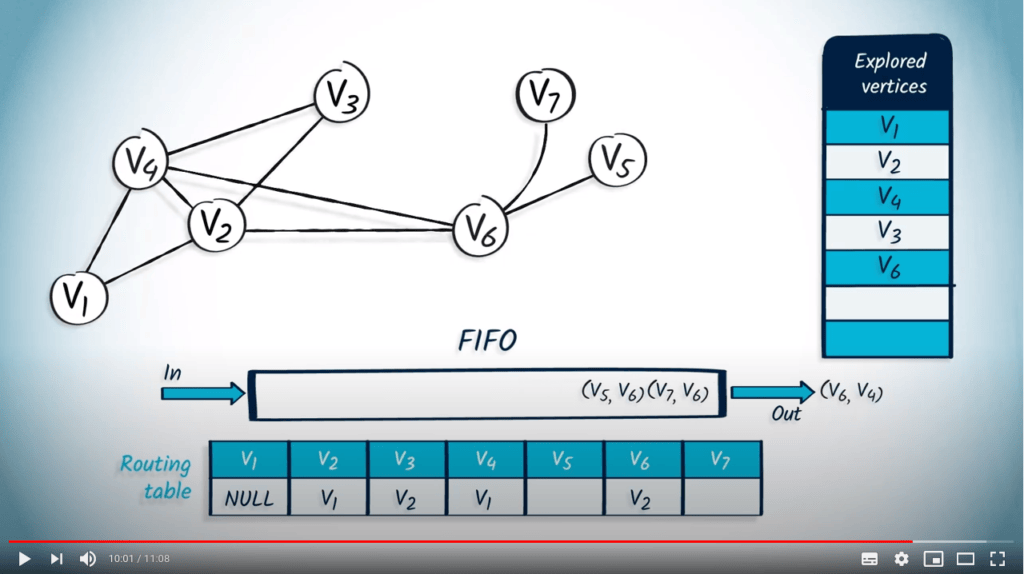
De même, $v_6$ avec $v_4$ est dépilé du FIFO, mais comme $v_6$ a déjà été exploré, nous passons au suivant.
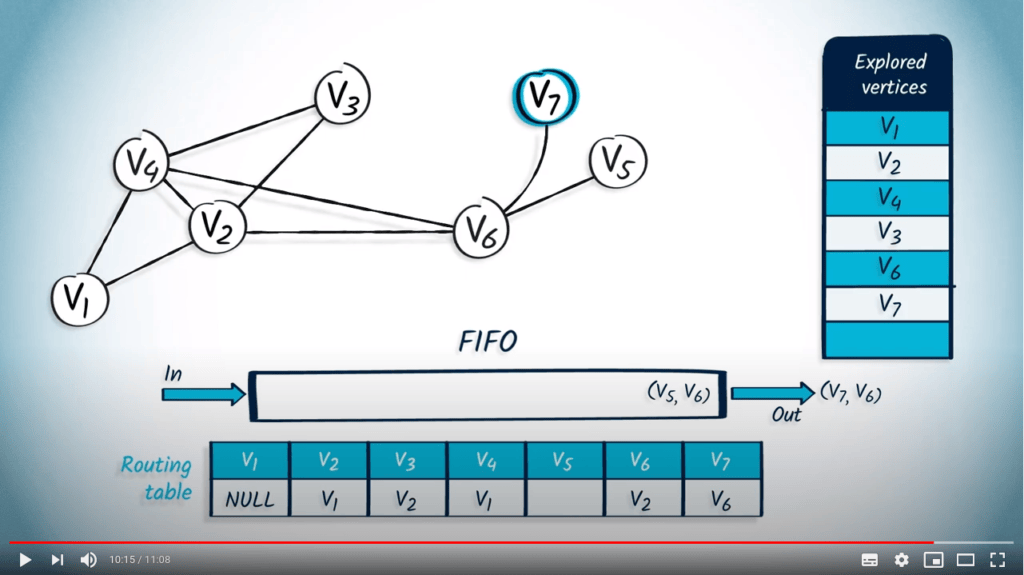
Maintenant, nous retirons du FIFO l'élément $v_7$ avec $v_6$ comme parent.
Le sommet $v_7$ n'avait pas été exploré auparavant, donc nous le marquons et mettons à jour la table de routage.
Le seul voisin de $v_7$ est $v_6$, qui a été exploré auparavant, donc nous continuons.
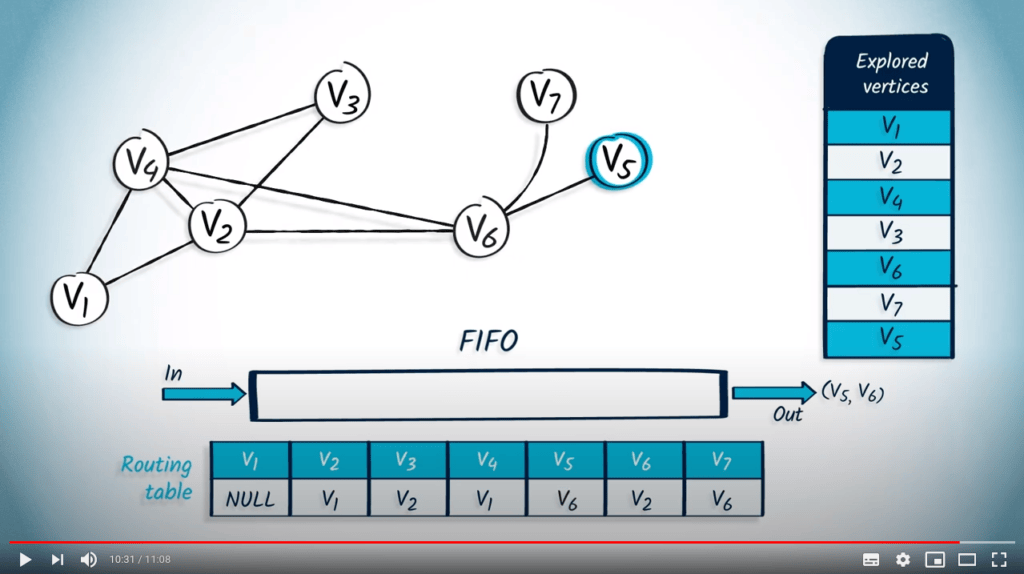
Enfin, nous dépilons $v_5$ avec $v_6$ comme parent du FIFO.
Le sommet $v_5$ n'est pas dans la liste des sommets explorés, donc nous l'ajoutons à cette liste, et mettons à jour la table de routage.
Ici encore, $v_5$ n'a pas de voisins non explorés.
La structure de file d’attente est maintenant vide, donc l’algorithme se termine.
Nous avons maintenant parcouru avec succès le graphe en utilisant BFS.
Mots de conclusion
Voilà comment vous pouvez utiliser des structures de file d’attente pour implémenter DFS et BFS.
Merci d’avoir regardé !
J’espère que vous avez apprécié apprendre sur les structures de file d’attente.
C’est la fin des leçons de cette semaine.
La semaine prochaine, nous verrons comment gérer les graphes pondérés.


































