Bonjour à tous ! Dans la leçon d’aujourd’hui, nous allons voir comment construire des tables de routage pour naviguer dans un graphe, en utilisant les arbres couvrants obtenus à partir des algorithmes de parcours de graphe, tels que le BFS ou le DFS.
Ces tables de routage aideront l’intelligence artificielle que vous développerez dans ce cours à se déplacer entre deux positions dans le labyrinthe.
Des arbres couvrants au routage
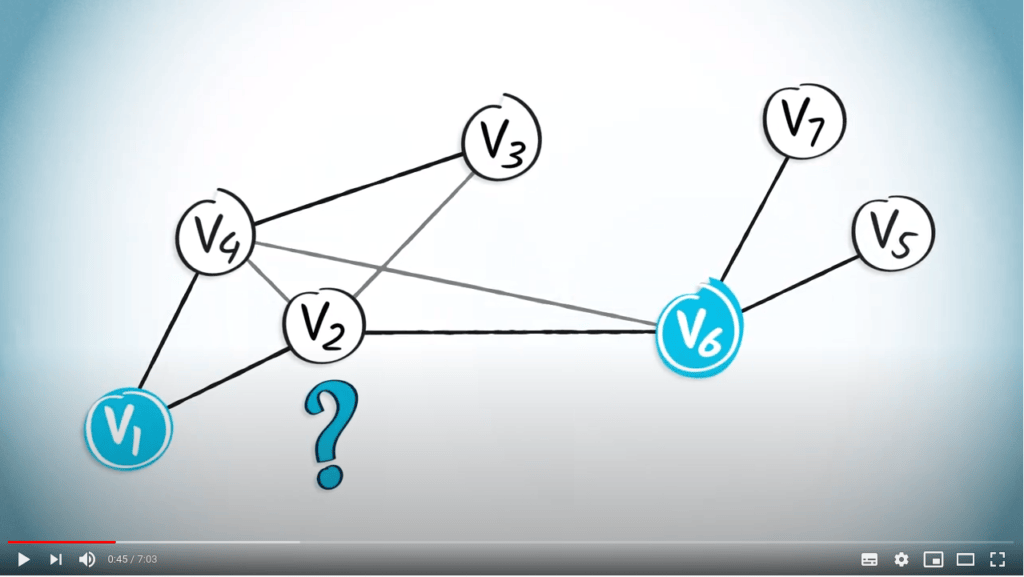
Dans la leçon précédente, vous avez appris comment construire des arbres couvrants. Une fois que nous avons un tel arbre couvrant, nous avons besoin d'un algorithme de routage pour pouvoir naviguer entre deux sommets quelconques du graphe.
Le routage d’un point de départ à une destination s’interprète à l’envers.
Nous connaissons déjà le point de départ, donc nous devons commencer par la destination pour trouver un chemin.
Ainsi, un algorithme de routage fournit un chemin de la destination au point de départ.
Tracer un chemin à l'envers est plus intuitif qu'il n'y paraît.
Imaginez que vous, le cercle bleu sur la carte, devez conduire jusqu'à la maison d'un ami, qui est le cercle orange sur la carte.
Vous pourriez commencer par décider si vous devez tourner à gauche ou à droite au prochain carrefour.
Puis, à chaque carrefour que vous rencontrez, identifiez quelle route peut être prise ensuite, jusqu'à ce que vous atteigniez finalement la maison de votre ami.
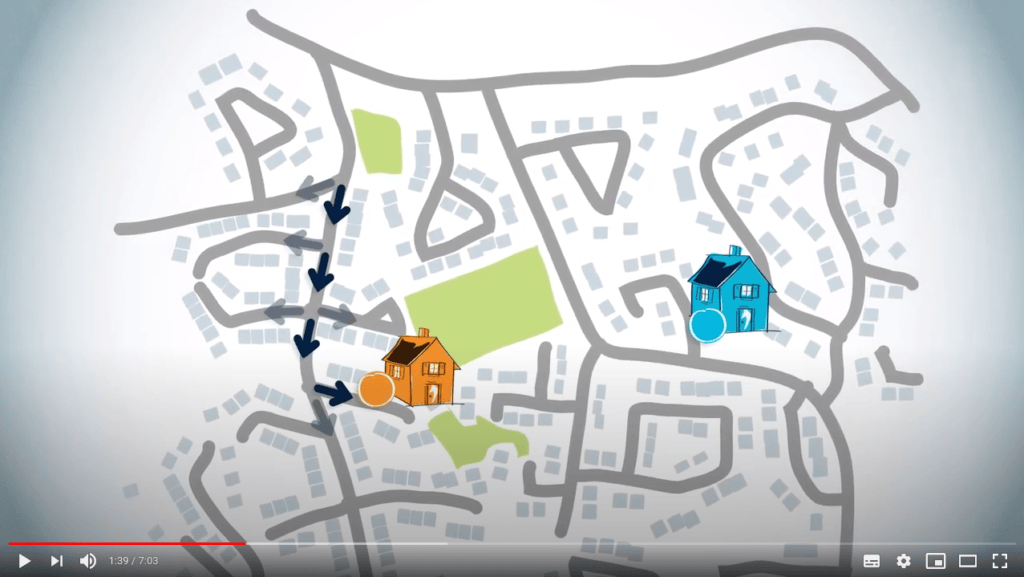
Ou bien, vous pourriez penser au meilleur itinéraire à l'envers, en identifiant d'abord dans quelle rue se trouve la maison de votre ami.
Puis, quelle autre route mène à cette rue, etc.
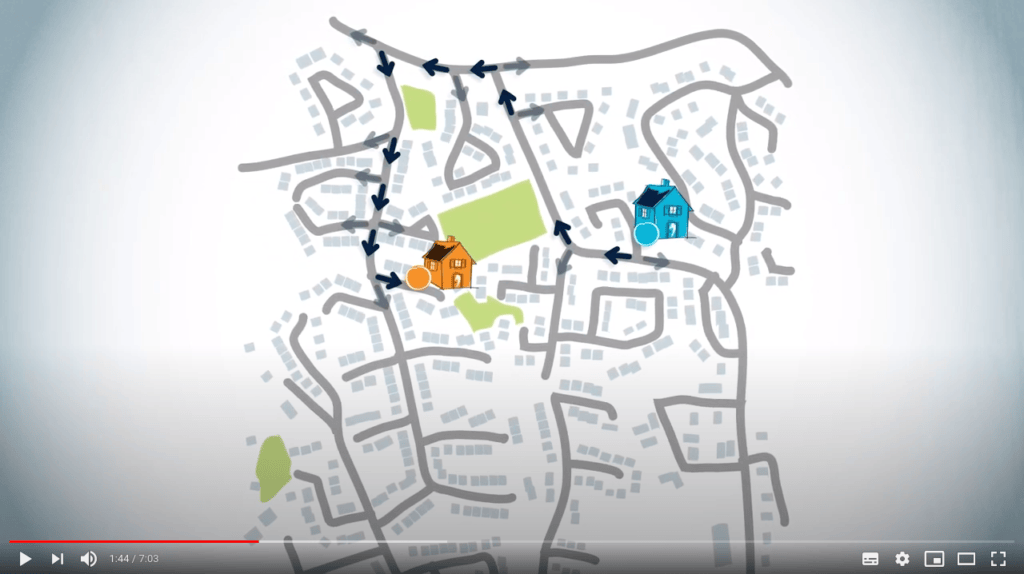
Jusqu'à savoir si vous devez tourner à gauche ou à droite au prochain carrefour.
Cette seconde façon de penser est celle que l’algorithme de routage va utiliser.
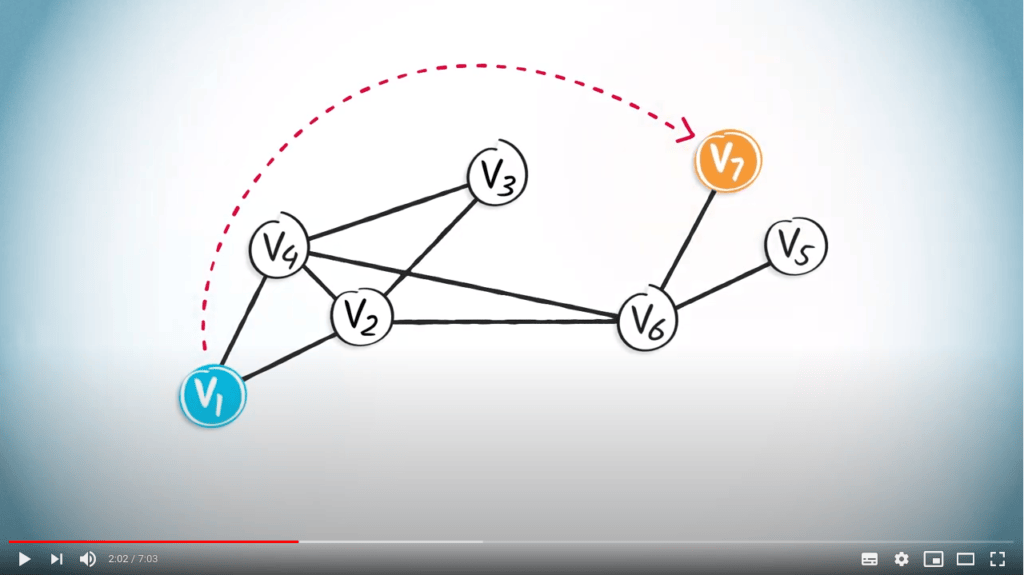
Pour mieux comprendre cela, regardons un exemple que nous avons déjà vu dans la leçon précédente que vous avez eue avec Vincent.
Considérons le chemin entre $v_1$ et $v_7$.
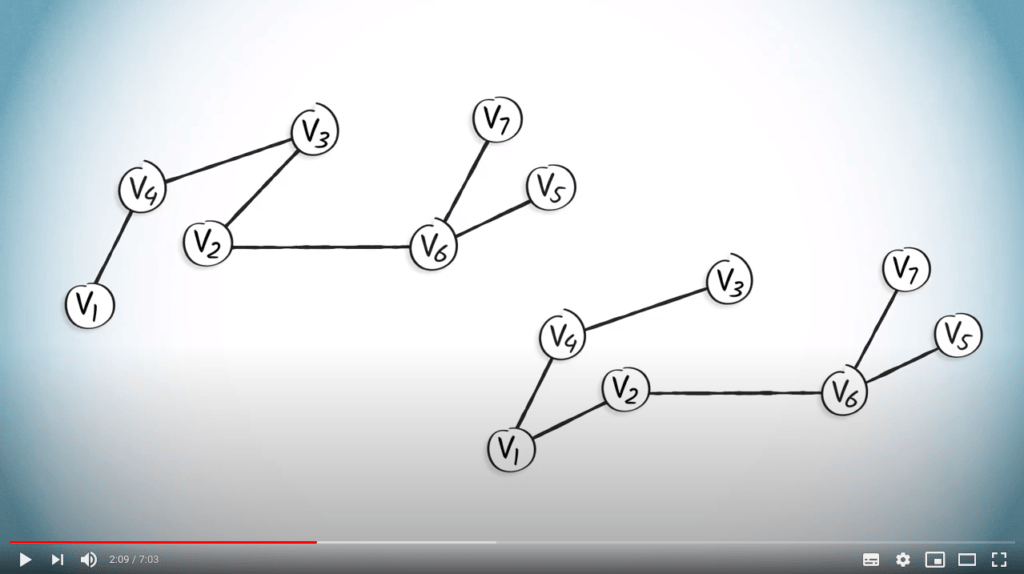
Nous pouvons voir l'arbre couvrant obtenu en utilisant un DFS à gauche, et l'arbre couvrant obtenu en utilisant un BFS à droite.
Le routage de $v_1$ vers n’importe quel autre sommet peut être facile lorsque nous utilisons des arbres.
Mais pour cela, nous avons d’abord besoin de quelques définitions supplémentaires.
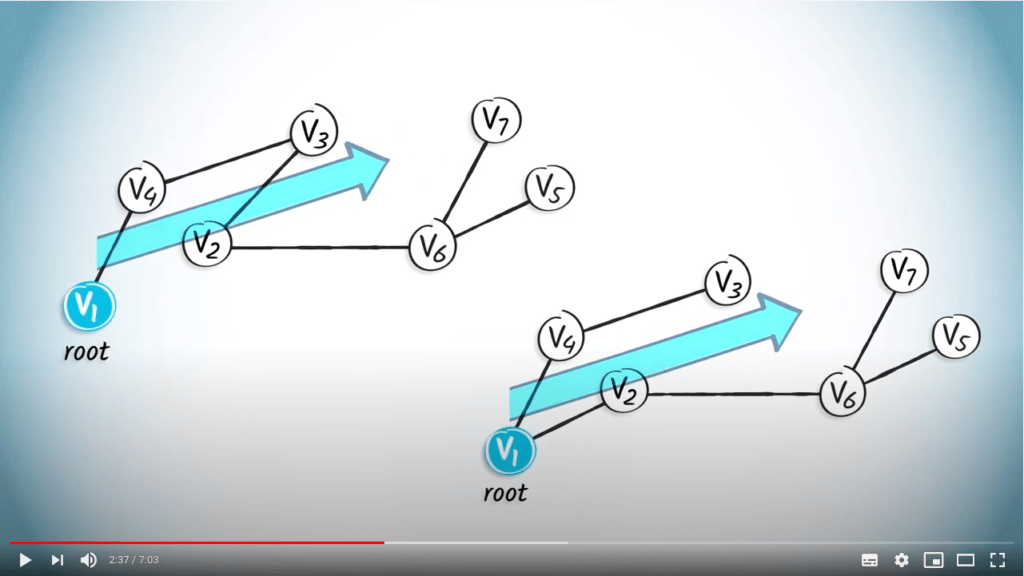
Un arbre enraciné est un arbre dans lequel nous désignons un sommet particulier comme racine, parfois appelé origine.
Dans ce cas, nous considérerons $v_1$ comme la racine, car c'est notre position de départ.
Par conséquent, les arêtes de cet arbre enraciné ont une orientation naturelle s'éloignant de la racine.
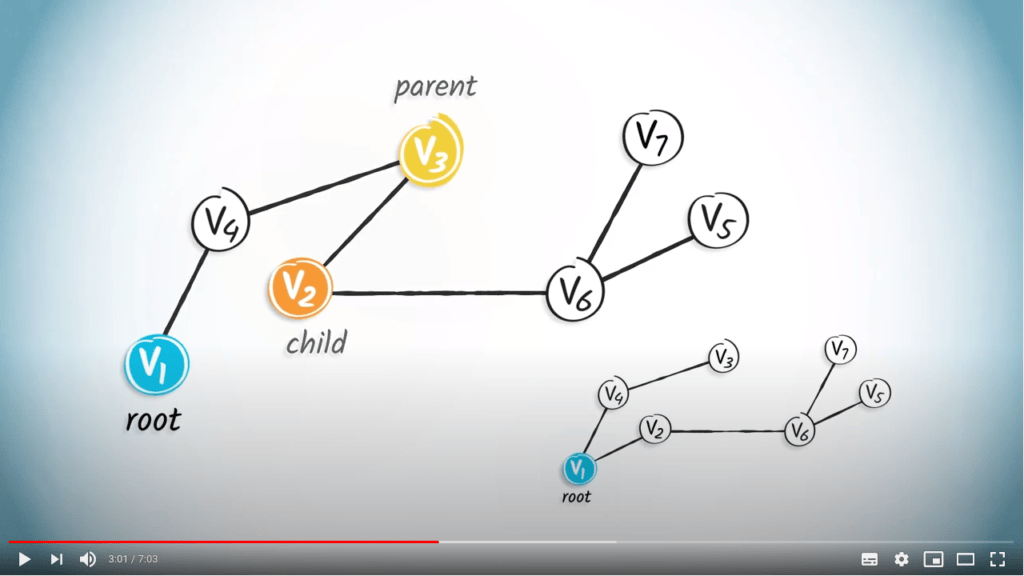
Dans un arbre enraciné, le parent d'un sommet est le sommet qui lui est connecté sur le chemin depuis la racine.
Par exemple, le parent de $v_2$ est $v_3$ dans l'arbre à gauche.
Chaque sommet sauf la racine a un seul parent.
Un enfant d'un sommet $v$ est un sommet dont $v$ est le parent.
Ainsi, $v_2$ est l'enfant de $v_3$ dans l'arbre à gauche.
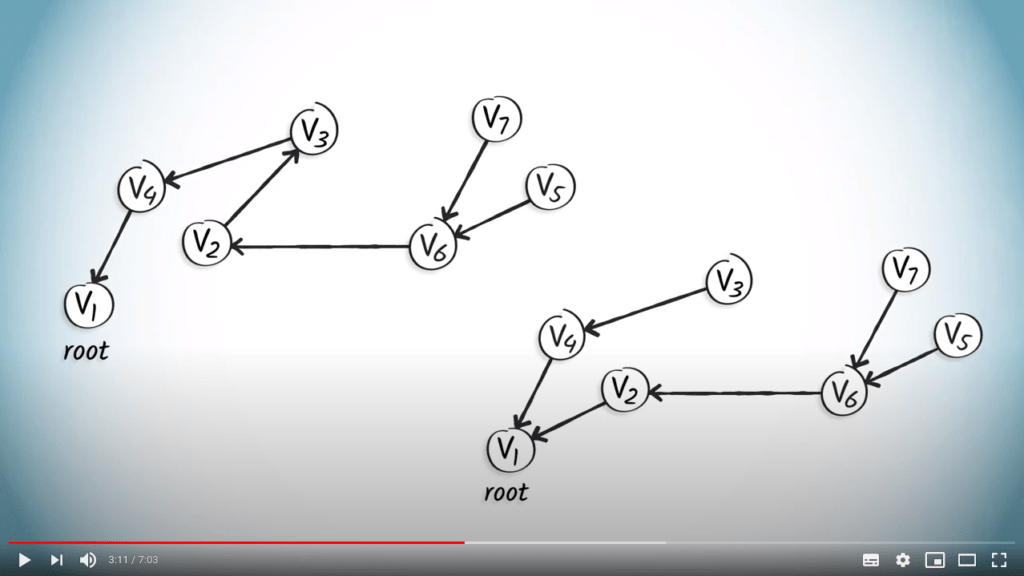
Si nous appliquons ces concepts à l'ensemble des arbres, nous obtenons les arbres enracinés suivants, où l'orientation des arêtes indique les parents des sommets.
Par exemple, dans les deux graphes, $v_1$ n'a pas de parent, le parent de $v_4$ est $v_1$, et les enfants de $v_6$ sont $v_7$ et $v_5$.
Tables de routage
Nous pouvons maintenant construire des tables de routage en considérant le parent de chaque sommet dans le chemin depuis $v_1$.
Les tables de routage sont des structures de données utiles qui peuvent être utilisées pour reconstruire un chemin.
Comme nous l’avons mentionné plus tôt, le routage est considéré à l’envers, de la destination vers la position de départ.
Une table de routage n'a qu'une seule ligne, et autant de colonnes qu'il y a de sommets dans le graphe.
Chaque colonne correspond à un sommet, et la valeur associée dans la table est son parent dans l'arbre couvrant enraciné en $v_1$.
Voyons maintenant comment cette table est construite étape par étape en utilisant un arbre couvrant.
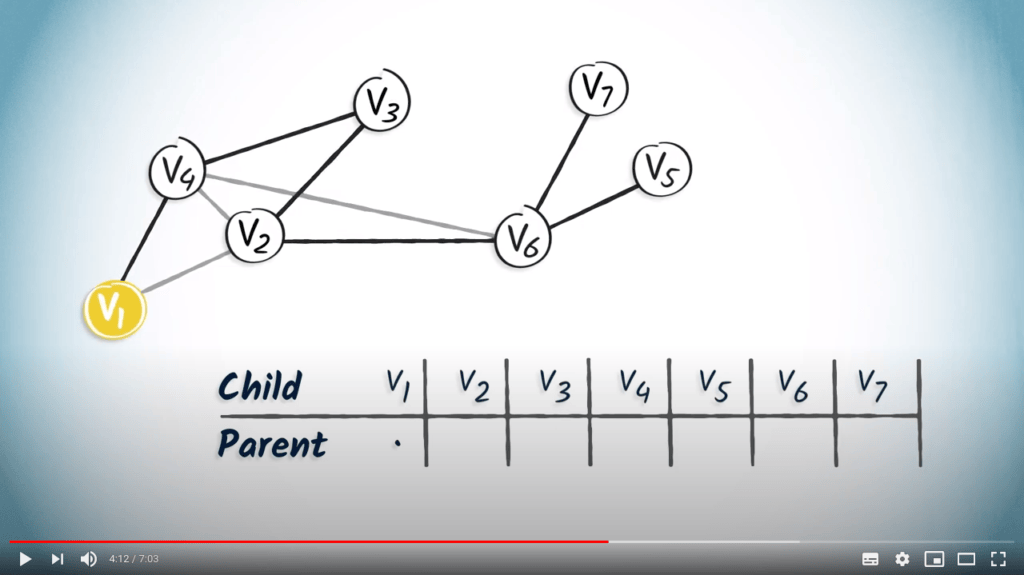
Commençons par un arbre obtenu à partir d'un DFS.
Nous commençons avec une table vide.
Le sommet $v_1$ est la racine, donc il n'a pas de parent.
Nous notons simplement un point dans la colonne $v_1$.
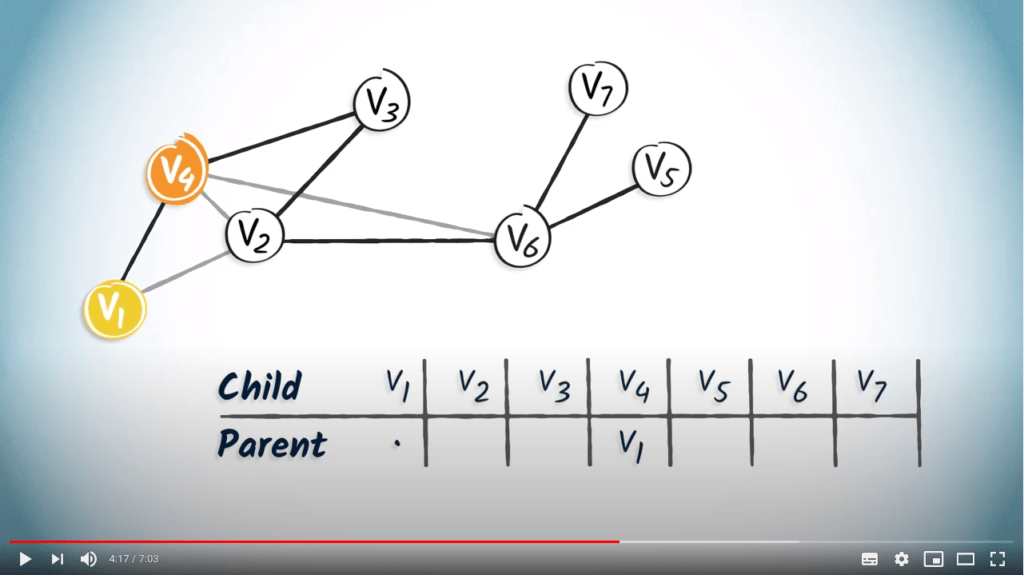
Le sommet $v_1$ n'a qu'un seul enfant, $v_4$.
Nous ajoutons donc $v_1$ dans la colonne correspondant à $v_4$.
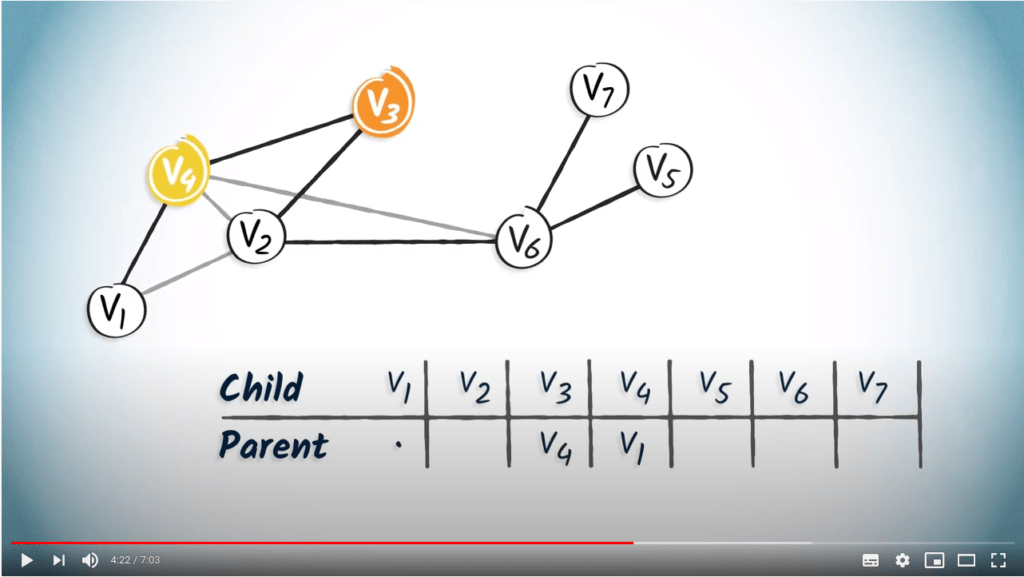
Le sommet $v_4$ n'a qu'un seul enfant, $v_3$.
Nous ajoutons donc $v_4$ dans la colonne de $v_3$.
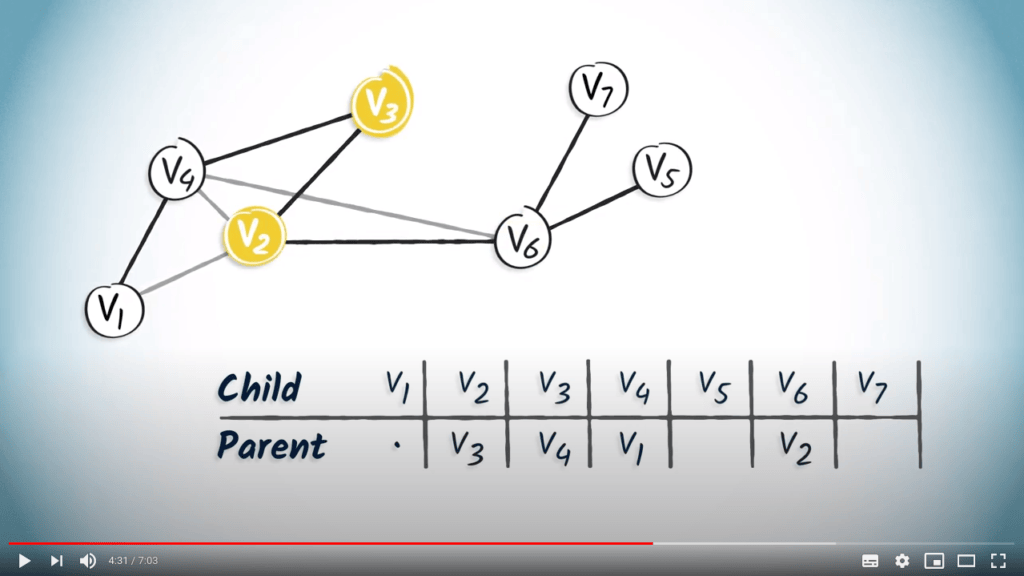
Appliquons maintenant simplement le même principe aux sommets $v_2$ et $v_6$, qui sont les seuls enfants de $v_3$ et $v_2$, respectivement.
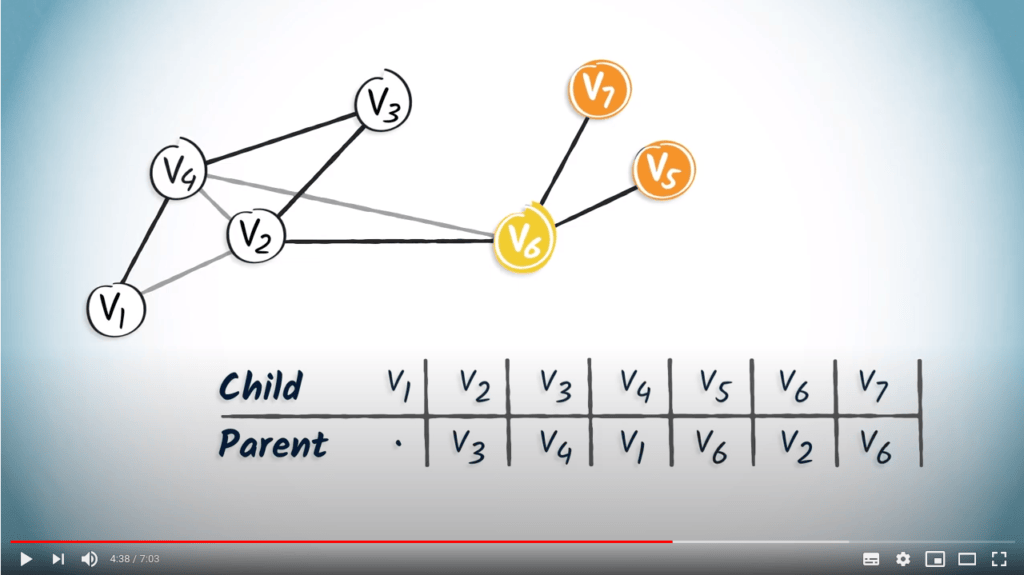
Enfin, $v_6$ a deux enfants, $v_7$ et $v_5$.
Ajoutons donc $v_6$ dans les colonnes correspondant à $v_5$ et $v_7$.
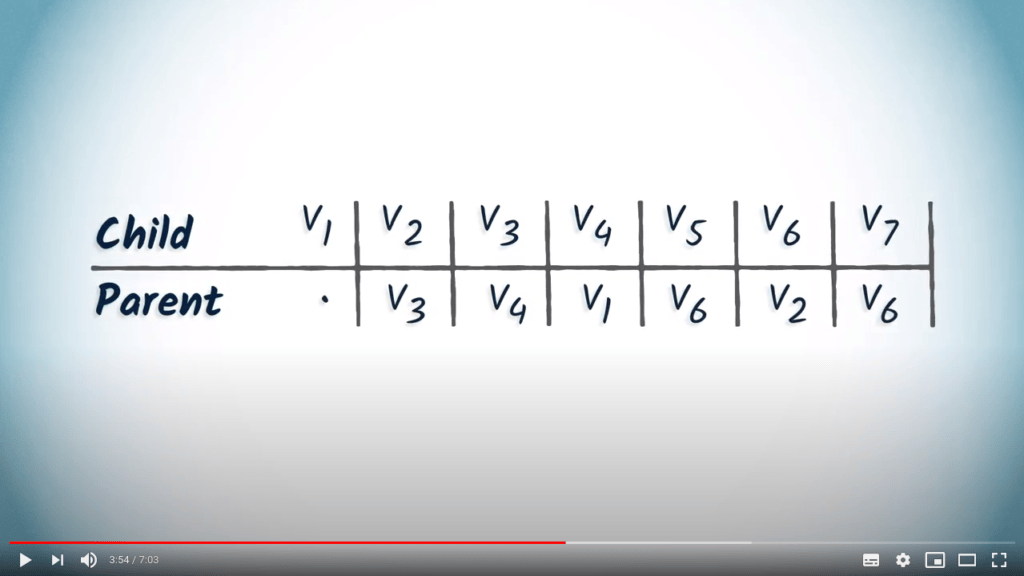
Voilà, la table de routage est complète.
Pour lire cette table, vous pouvez simplement commencer par la destination souhaitée et lire l’entrée correspondante, qui fait référence au sommet parent de la destination.
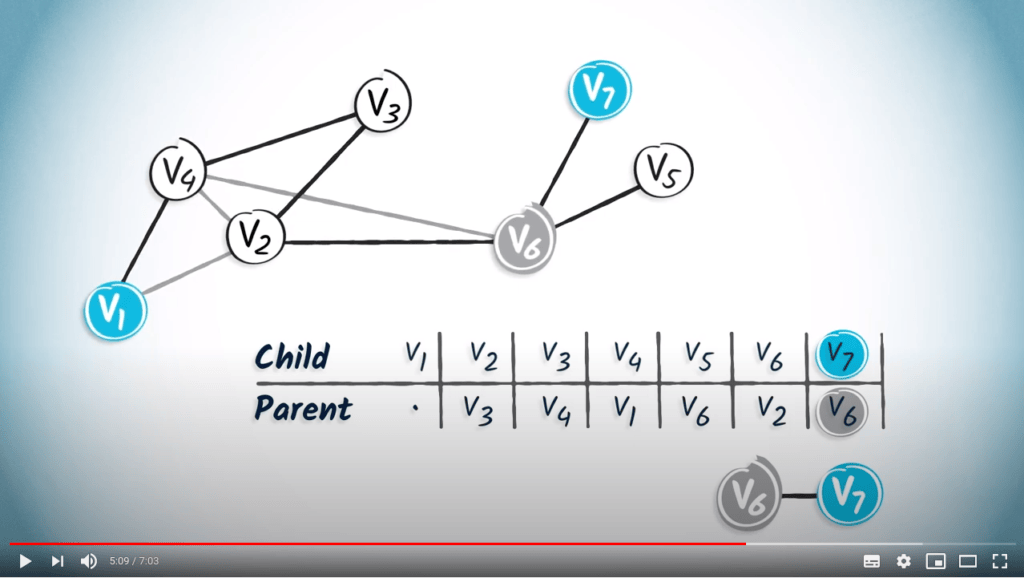
Par exemple, si nous cherchons le chemin de $v_1$ à $v_7$, nous lisons d'abord l'entrée correspondant à $v_7$, qui est $v_6$.
Par définition, le parent de la destination correspond à son tour au sommet précédent dans le chemin de $v_1$ à la destination.
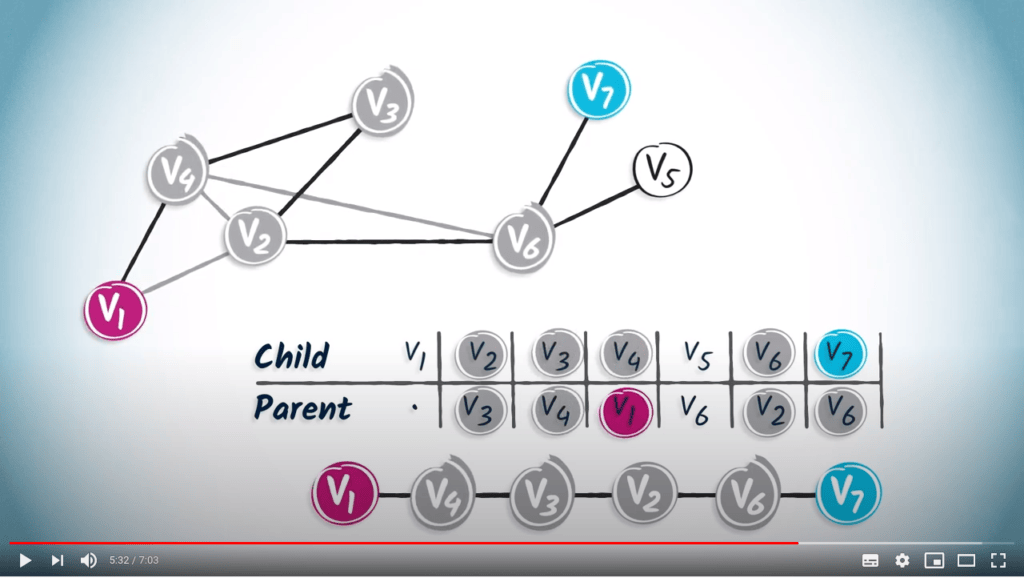
En lisant les entrées correspondant à chaque prédécesseur, vous atteindrez finalement la position de départ $v_1$.
Donc, dans notre exemple, l'étape suivante est d'identifier l'entrée correspondant à $v_6$, qui est $v_2$.
En continuant ainsi, nous obtenons le chemin $(v_7, v_6, v_2, v_3, v_4, v_1)$.
Comme deuxième exemple, construisons également la table de routage à partir de l’arbre couvrant obtenu par un BFS.
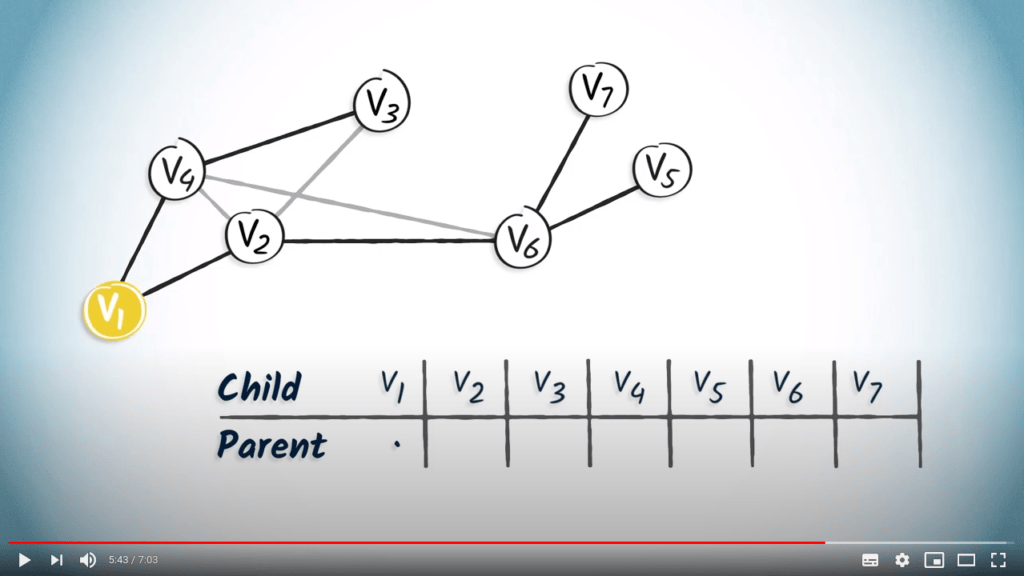
Voici l'arbre couvrant. Encore une fois, nous commençons avec une table vide.
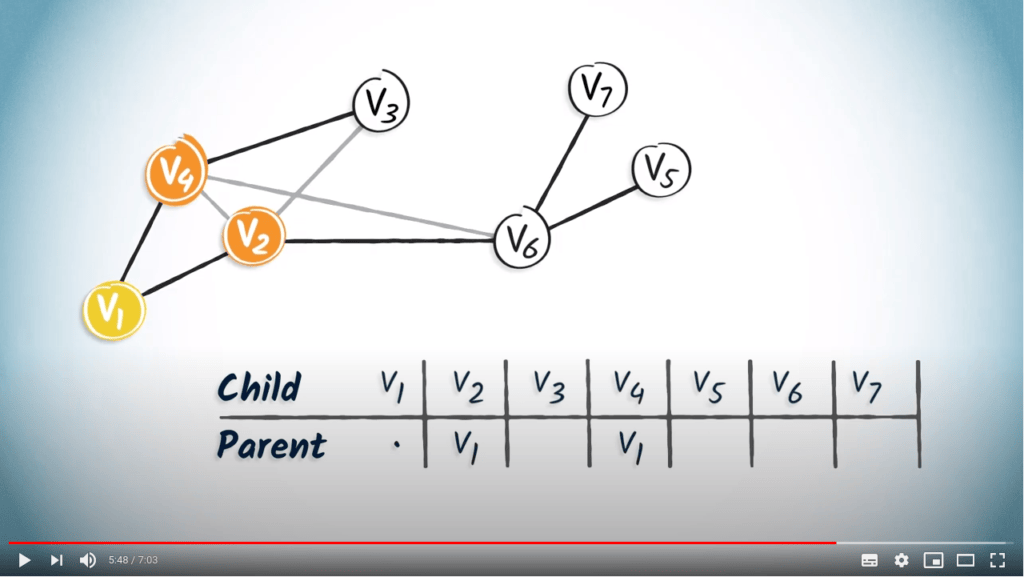
Le sommet $v_1$ a deux enfants, $v_4$ et $v_2$.
Nous ajoutons donc $v_1$ dans les colonnes correspondantes.
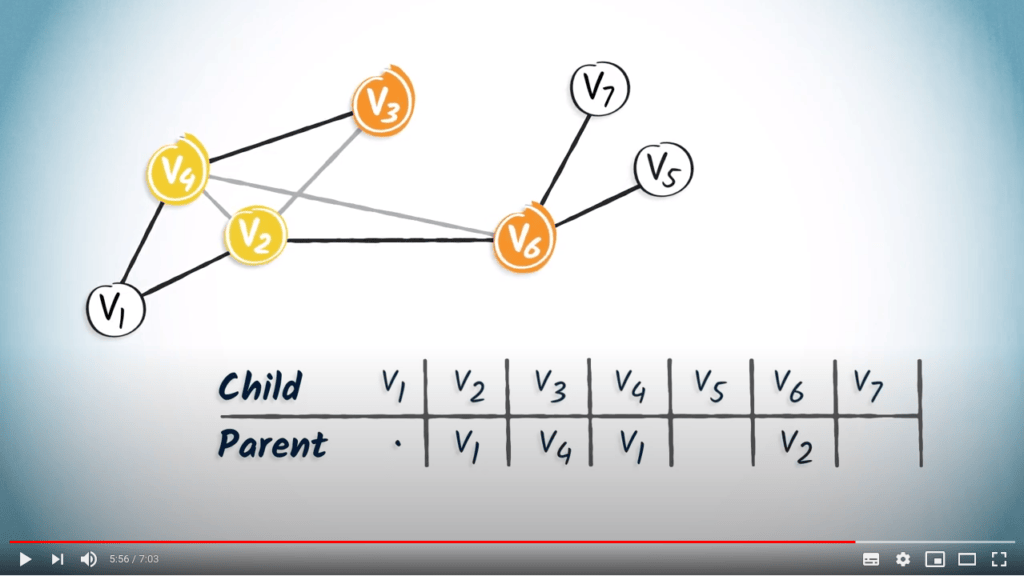
Le seul enfant de $v_4$ est $v_3$, et le seul enfant de $v_2$ est $v_6$.
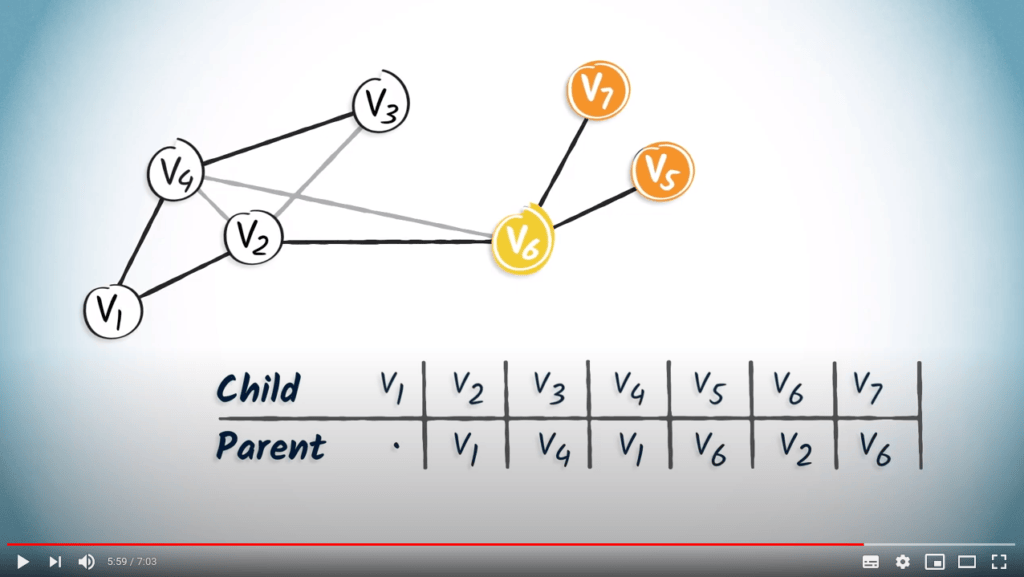
Ensuite, $v_6$ a deux enfants, $v_7$ et $v_5$.
La table de routage est complète.
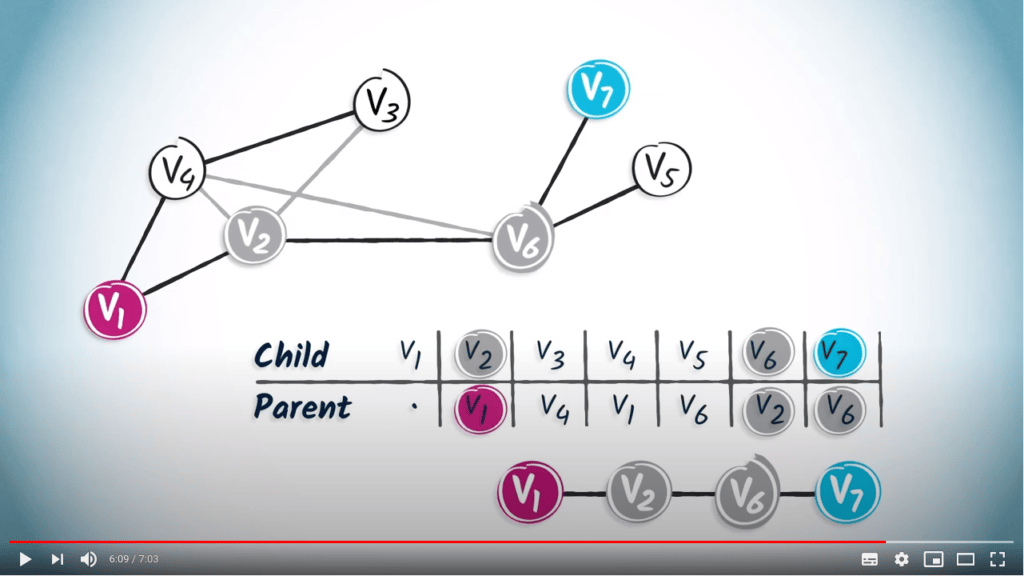
Si nous lisons le chemin de $v_1$ à $v_7$ dans la table, nous obtenons $(v_7, v_6, v_2, v_1)$.
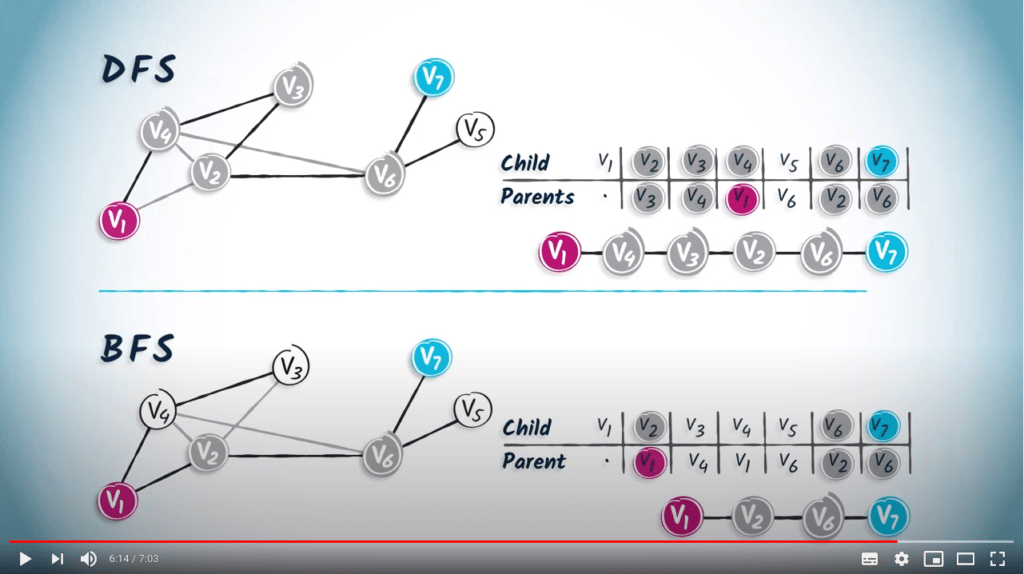
Nous pouvons voir que ce chemin est plus court que celui obtenu avec un DFS, qui était $(v_7, v_6, v_2, v_3, v_4, v_1)$.
C'est une différence importante entre DFS et BFS.
BFS est une approche plus prudente que DFS, car BFS augmente progressivement la distance depuis la position de départ.
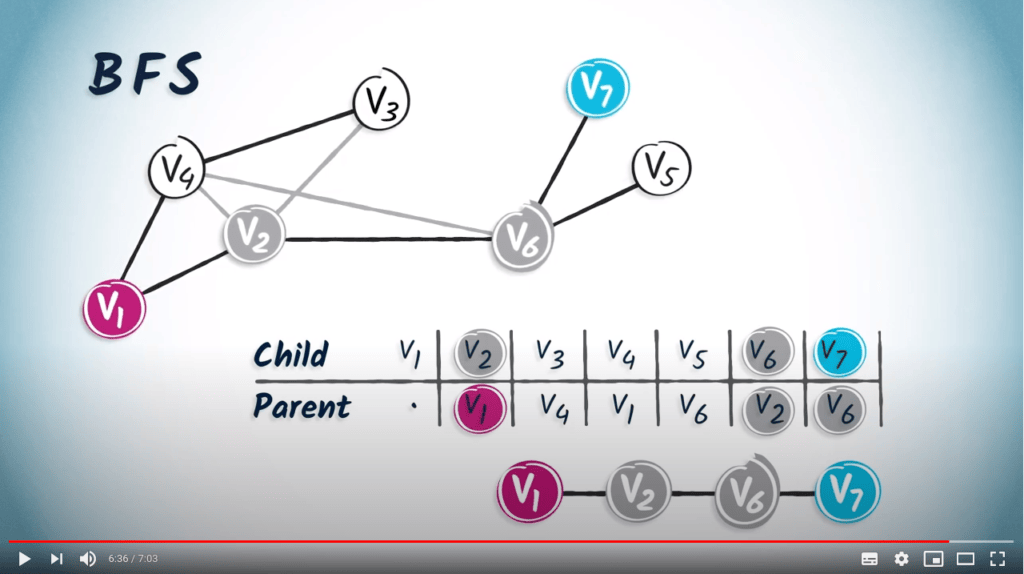
En utilisant BFS, nous pouvons être absolument certains de trouver le chemin le plus court entre deux sommets.
Mots de conclusion
C’est tout pour aujourd’hui.
Merci pour votre attention !
J’ai vraiment apprécié parler de routage avec vous.
Vous devez vous souvenir qu’il ne suffit pas de construire l’arbre couvrant pour naviguer entre les sommets du graphe, mais qu’il faut aussi un algorithme de routage.
À bientôt pour d’autres aventures algorithmiques !

























