Greedy algorithms

Salut ! C’est encore moi. Je vois que vous avez faim d’en apprendre plus sur la théorie des graphes. Moi aussi !

Parfois, quand un problème est trop complexe à résoudre, on utilise des algorithmes approximatifs. Les algorithmes approximatifs fournissent une solution proche de la solution exacte, mais en beaucoup moins de temps. Un exemple d’algorithmes approximatifs sont les algorithmes gloutons.

Principe

Le but d’un algorithme glouton est d’approximer la solution à un problème par une succession de solutions localement optimales. Pour illustrer cela, considérons le problème du voyageur de commerce, le TSP, que nous avons vu être un problème complexe à résoudre.

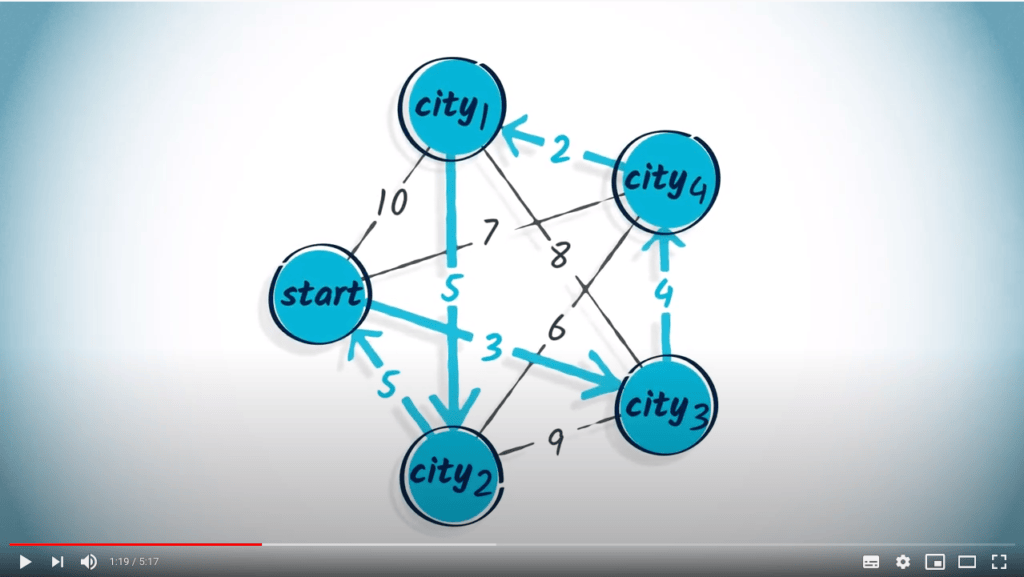
Au lieu de chercher une solution exacte, on peut choisir d'aller toujours vers le sommet inexploré le plus proche du sommet où nous nous trouvons actuellement. C'est un algorithme glouton car, à chaque étape, la distance à parcourir est minimisée, une étape à la fois. Ainsi, nous avons pris des décisions localement optimales.

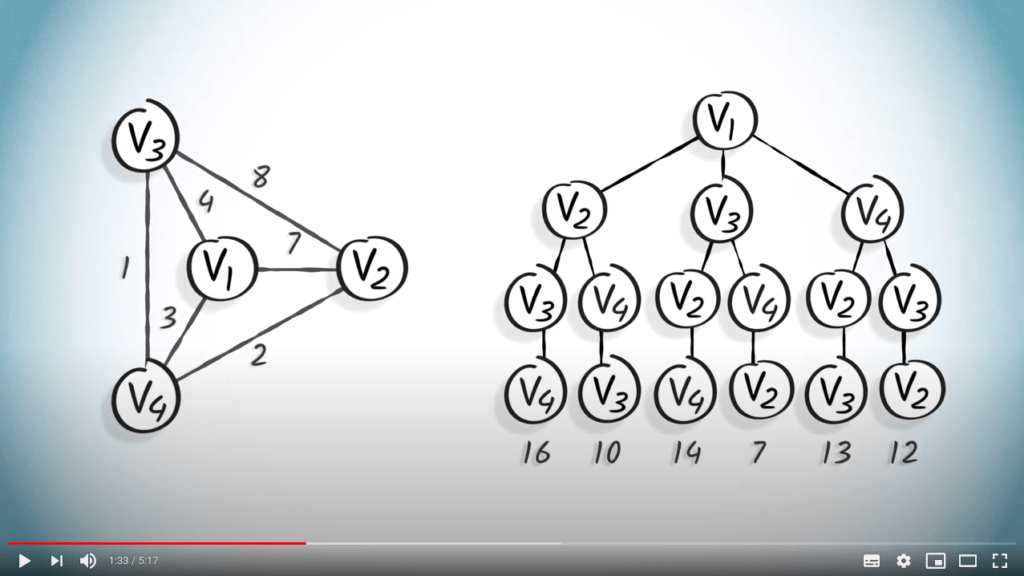
Cependant, cette solution n'est pas nécessairement optimale. Prenons l'exemple du graphe suivant, pour lequel nous explorons tous les chemins possibles.

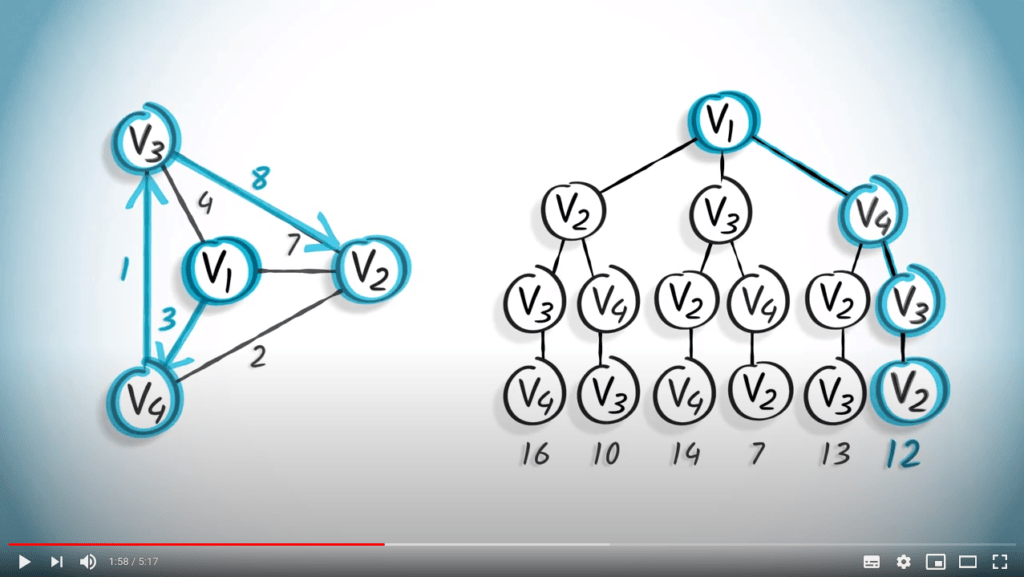
Mettons l'algorithme glouton en pratique. En partant du sommet $v_1$, nous irons d'abord à $v_4$, car l'arête correspondante est la plus courte parmi toutes les possibilités. En suivant le même principe, nous irons ensuite à $v_3$ puis enfin à $v_2$. N'est-ce pas ? Dans cet exemple, le chemin obtenu a une longueur totale de 12.

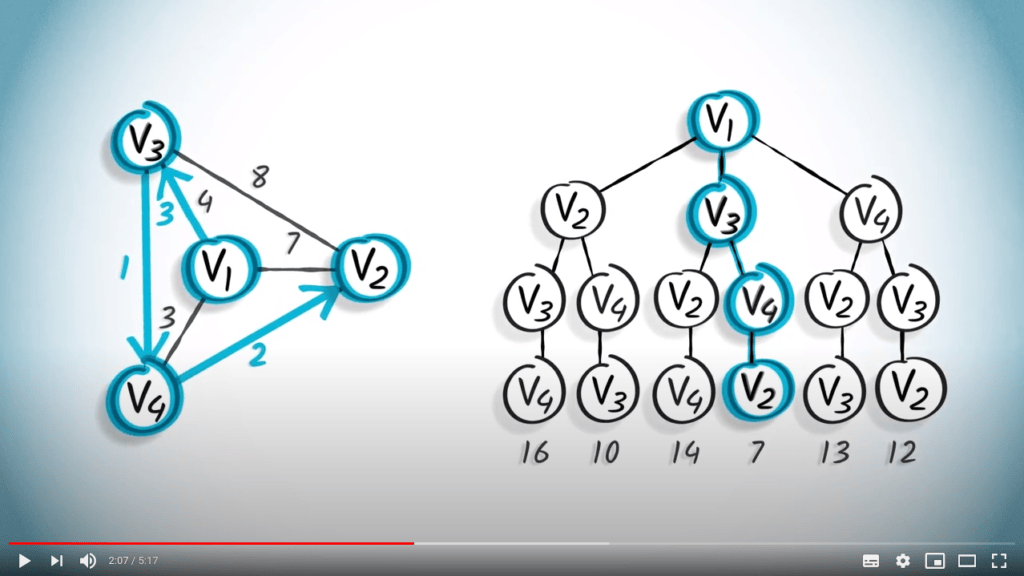
Cependant, la solution optimale est un chemin de longueur 7, qui est le chemin $( \{v_1,v_3\}, \{v_3,v_4\}, \{v_2,v_4\} )$.

N’oubliez pas, cet algorithme n’est qu’un exemple d’algorithme glouton pour répondre au TSP. En plus de choisir systématiquement le voisin le plus proche, comme dans l’exemple que nous venons de voir, d’autres heuristiques peuvent être utilisées. Voici quelques exemples :

Vous pouvez choisir le chemin de longueur minimale en explorant $k$ sommets restants ($k = 2, 3, \dots$) ? Si $k = 1$, alors c’est l’algorithme glouton simple que nous venons de voir, Vous pouvez choisir d’aller vers une zone dense d’un labyrinthe où il y a beaucoup de morceaux de fromage à trouver, Ou, vous pouvez choisir de lancer aléatoirement plusieurs recherches possibles, et retenir la meilleure option.

Un cas où l’algorithme glouton est optimal

Dans certains cas, les algorithmes gloutons peuvent être optimaux.

Considérons le problème de rendre la monnaie après un paiement. Nous souhaitons rendre une certaine somme en euros, et nous disposons des pièces suivantes : 1c, 2c, 5c, 10c, 20c, 50c, 1€, 2€. Le but est d'utiliser le moins de pièces possible.

Un algorithme glouton typique est de sélectionner la pièce de la plus grande valeur possible, inférieure à la somme à rendre, jusqu'à ce que la monnaie restante à rendre soit 0. Donc, si vous voulez rendre 3,27€, l'algorithme rendra d'abord 2€ (il reste 1,27€ à rendre), puis 1€ (il reste 27c à rendre), 20c (il reste 7c à rendre), 5c (il reste 2c à rendre), et enfin 2c.

En examinant toutes les combinaisons possibles, on peut voir que c’est effectivement la solution optimale. Pour le montrer, il suffit de remarquer que chaque pièce a une valeur au moins égale au double de la pièce de valeur inférieure. Cela signifie qu’il sera toujours plus efficace de donner la priorité à la pièce de plus grande valeur, car une seule pièce sera rendue au lieu de plusieurs.

Maintenant, considérons les pièces suivantes : 1c, 2c, 5c, 10c, 20c, 40c, 50c, 1€, et dans ce cas nous voulons rendre 80c. L'algorithme glouton rendra 50c (30c restants), puis 20c (10c restants) et 10c, c'est-à-dire trois pièces.

Cependant, rendre 80c peut aussi se faire en rendant deux pièces de 40c. Dans ce cas, un algorithme glouton n'est pas optimal.

Mots de conclusion

Pour résumer, cette leçon vous a introduit aux algorithmes gloutons pour trouver des solutions approximatives à des problèmes complexes tels que le TSP.

À la prochaine !