Notation UML pour la modélisation conceptuelle des données
Temps de lecture30 minRésumé
La modélisation conceptuelle des données est une approche fondamentale pour concevoir des bases de données structurées et cohérentes, servant de pont entre le monde réel et l’implémentation technique.
Points essentiels
- La modélisation conceptuelle offre une représentation intuitive des données complexes
- La notation UML fournit les outils pour représenter les classes, associations et contraintes
- Les cardinalités permettent d’exprimer précisément les relations entre entités
- Différents types d’associations (binaires, n-aires, réflexives) permettent de modéliser des situations variées
- L’héritage permet d’organiser hiérarchiquement les concepts et leurs propriétés
Introduction
La modélisation conceptuelle est une approche intuitive pour concevoir une base de données. Elle est adaptée dès qu’on doit structurer un ensemble de données un peu complexe (à chacun de juger quand un ensemble de données atteint ce seuil). Une autre approche, la théorie de la normalisation, est plus formelle, plus rigoureuse et offre des moyens d’analyse très fins pour régler des problèmes sur des sous-ensembles précis des données.
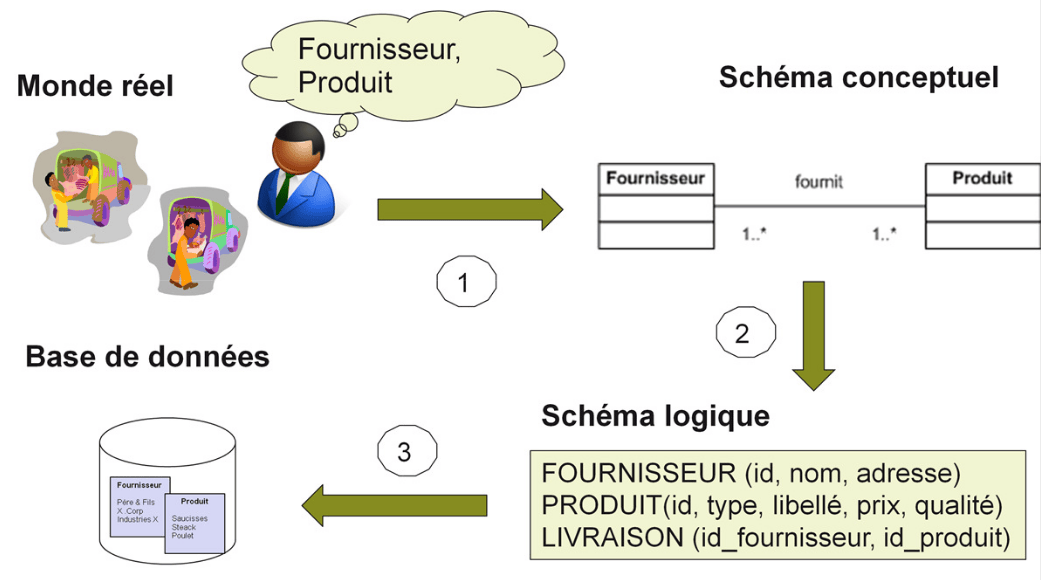
Sur ce schéma, on montre où se situe la modélisation conceptuelle de données. Entre le monde réel qu’elle doit permettre de représenter de manière assez intuitive et les modèles logiques des SGBD sous-jacents.
Au bénéfice des modèles conceptuels, on peut dire qu’il est souvent plus simple (plus intuitif) de passer par une modélisation conceptuelle entre le monde réel et la modélisation logique (dans notre cas, la modélisation relationnelle).
L’étape intermédiaire de transformation d’un modèle conceptuel vers un modèle logique s’appelle la dérivation. La limite des modèles conceptuels est liée à ce qui fait leur force : si l’expert qui modélise les données n’a pas la bonne intuition, alors le modèle ne met pas de garde-fous pour aider l’utilisateur dans sa démarche, contrairement à des formalismes logiques plus formels, tels que le modèle relationnel qui s’accompagne d’un formalisme de modélisation très rigoureux (appelé « théorie de la normalisation »).
Les séances dédiées à la théorie de la normalisation illustrent ainsi la complémentarité que l’on peut trouver entre la modélisation conceptuelle (utile quand les données sont complexes) et la modélisation relationnelle (permettant, sur un ensemble de données restreint, d’avoir une démarche rigoureuse).
La notation UML
Les notations UML présentées dans ce document sont présentées dans l’optique d’effectuer un modèle conceptuel de données. Afin d’effectuer un diagramme de classe, les mêmes éléments de notation sont utilisés, mais les usages peuvent parfois sensiblement différer.
Les classes
Une classe est un objet concret ou abstrait qui a une existence propre et qui permet de décrire un concept dans le système d’information.

Dans cet exemple, nous allons évoquer deux classes : Étudiant et Livre.
Les associations binaires (dimension 2)
Une association binaire est un groupement de deux classes pour décrire une réalité de l’organisation.

Les associations permettent de représenter les règles de gestion d’une organisation. Ici, nous voulons exprimer le fait qu’un étudiant puisse emprunter un livre.
Les contraintes de cardinalités
La cardinalité indique le nombre d'instances d'une classe qui sont associées à chacune des instances de l'autre classe.

Les cardinalités s’écrivent au moyen d’un couple de valeurs permettant d’exprimer les cardinalités minimale et maximale. En UML, la cardinalité caractérisant l’association d’une classe A à une autre classe B s’écrit à l’opposé de la classe A, près de la classe B.
Par exemple, en observant l’exemple ci-dessus, nous pouvons dire :
- Un étudiant (instance de la classe
Etudiant) peut avoir emprunté aucun ou plusieurs livres : cardinalité 0..* du côté deLivre. - Un livre (instance de la classe
Livre) peut ne pas avoir été emprunté par un étudiant, ou avoir été emprunté une seule fois : cardinalité 0..1 du côté deEtudiant.
Les différents types d’association
A partir de cette notion de cardinatité nous pouvons ainsi caractériser 3 grands types d’association :
- Les associations un-à-un notées 1:1
- Les associations un-à-plusieurs notées 1:N
- Les associations plusieurs-à-plusieurs notées N:M (ou N:N)
Ici quand on parle d’une cardinalité de type “1” on évoque les couples de cardinalités (0..1) et (1..1). Quand on parle d’une cardinalité de type “N” on évoque les couples de cardinaliltés (0..*) et (1..*).
Dans notre exemple précédent, l’association emprunt entre Etudiant et Livre est une association 1:N (un à plusieurs).
Les propriétés
Une propriété désigne une valeur ou un groupe de valeurs pour décrire une classe ou une association entre classes.

Les associations portées
Une association N:M peut avoir en propre des propriétés. Cela n’est en aucun cas obligatoire.

Dans cet exemple, un étudiant peut avoir aucun ou plusieurs abonnements (à une revue), et une revue être concernée par aucun ou plusieurs abonnements (d’étudiants). Ici les attributs date_début et durée caractérisent l’association entre les deux entités.
Les associations réflexives
Une association réflexive est une association binaire qui relie une classe avec elle-même.

Dans cet exemple, chaque personne est associée à un seul et unique manager, c’est-à-dire que chaque personne apparait une seule et unique fois en tant qu’employé dans l’association entre manager et employé.
Par ailleurs, chaque manager est associé à aucun ou plusieurs employés, c’est-à-dire que chaque personne apparait aucune ou plusieurs fois en tant que manager dans l’association entre manager et employé.
Les associations n-aires (dimension n)
On généralise le concept d’association binaire à un nombre quelconque de classes. Le schéma ci-dessous montre l’exemple d’une association ternaire, de dimension 3.
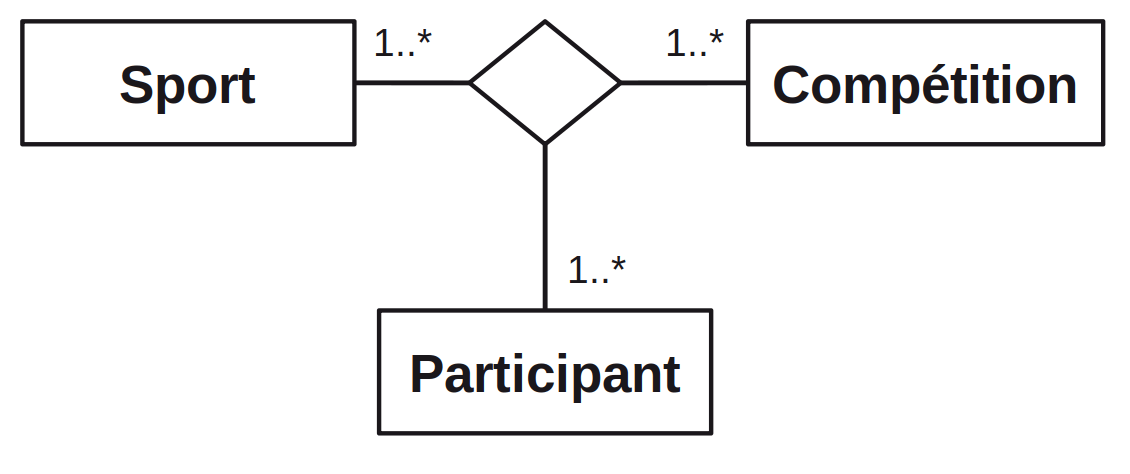
Dans cet exemple, l’association ternaire représente l’inscription d’un participant à un sport pour une compétition donnée. Pour déterminer les cardinalités il faut se poser 3 questions :
- Pour une compétition donnée et un participant donné, à combien de sports peut on s’inscrire ?
- Pour une compétition donnée et un sport donné, combien de particants peuvent-ils s’inscrire ?
- Pour un participant et un sport donné, à combien de compétition peut on s’inscrire ?
Dans notre exemple la réponse est à chaque fois 1 fois ou plusieurs.
L’héritage
L’héritage permet d’exprimer des propriétés communes à plusieurs classes : il peut être exclusif ou non exclusif
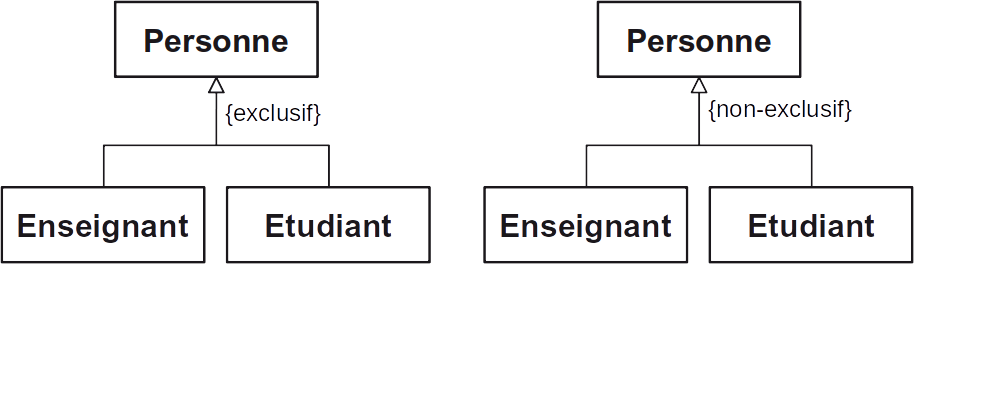
- Héritage exclusif : une personne ne peut pas être à la fois un enseignant et un étudiant.
- Héritage non exclusif : un étudiant peut également être un enseignant (par exemple un doctorant).
Conclusion
La modélisation conceptuelle des données avec UML constitue une étape cruciale dans la conception de bases de données. Elle offre plusieurs avantages clés :
- Une représentation visuelle claire facilitant la communication entre les différents acteurs
- Une approche intuitive adaptée aux données complexes
- Une transition naturelle vers le modèle relationnel
- Une documentation précieuse pour la maintenance future
Cependant, elle présente aussi certaines limites :
- Elle repose fortement sur l’intuition du modélisateur
- Elle nécessite une bonne compréhension des besoins métier
- Elle doit être complétée par des approches plus formelles pour certains aspects