Queues

Reading time10 min

In brief

Article summary

In this article, we present you a data structure called “queue”. With this structure, elements are removed in the order in which they are added.

Two possible implementations of a queue are discussed. One is introduced here, and the other one is the subject of the practical session. It is shown that they can be used independendly if the primitives abstract the details.

Main takeaways

  • Queues are data structures where the first element to be added is the first element to be removed.

  • Depending on implementation of the queue, some operations may take longer than others.

  • Using primitives allows to hide implementation details.

Article contents

1 — What is a queue?

A queue is a data structure with restricted access as the first element in is the first element out. This access method is called FIFO (First In, First Out). Managing a queue consists in adding elements at the end of the queue (enqueue) and removing elements at the beginning (dequeue).

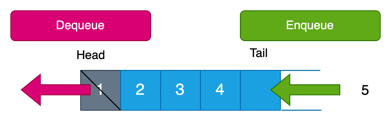
Queue operations

Queues are less common in algorithms than stacks because their scope is less extensive. However, there are areas where they are useful, such as managing the flow of people at a counter, where the first to arrive is the first to be served.

2 — Primitives

In a program using a queue, the implementation details of the data are abstracted away. The program simply queues or dequeues elements from the queue using sub-programs known as “management primitives”. The main primitives for queue operations are:

  • initialize – Initializes the queue.
  • push – Adds an element to the end of the queue.
  • pop – Removes the first element from the queue.
  • is_empty ** Returns true if the queue is empty, and false otherwise.

Like stacks, queues can be implemented as “arrays” or “linked lists”.

3 — Implementation of queues

In practice, each programming language offers a proper implementation of a queue. Here, we show possible implementations for pedagogical purpose.

3.1 — Use of a list

Managing a queue can be done by adding elements to the beginning of the list (enqueuing) and removing elements at the end of the list (dequeuing), or vice versa.

Here is a possible implementation of a queue, using a list to store information:

​
"""
    This module provides an implementation of the primitives to handle a queue of values. 
    The queue is materialized by means of a list with a size limit to simulate an array.

"""

# Needed imports
from typing import List,Any

# Define your own custom type
Queue = List[Any]



def initialize() -> Queue:

    """
        Initializes an empty queue.
        In:
            * None.
        Out:
            * An empty queue.
    """

    # We use lists to represent queues
    return []



def is_empty (queue: Queue) -> bool:

    """
        This function checks if the queue is empty.
        In:
            * queue: Queue to check.
        Out:
            * True if the queue is empty, False otherwise.
    """

    # Check list length
    return len(queue) == 0



def push (queue: Queue, item: Any) -> None:

    """
        This function adds an element to the queue.
        The element is added at the last position of the storage structure.
        In:
            * queue: Queue to modify.
            * item:  Element to add.
    """

    # Add the element to the end of the list
    queue.append(item)



def pop (queue: Queue) -> Any:
    
    """
        This function removes the next element of the queue.
        In:
            * queue: Queue to modify.
        Out:
            * The next element of the queue.
    """
    
    # Extract and return the first element of the list
    return queue.pop(0)



def display (queue: Queue) -> None:
    
    """
        This function displays the content of the queue.
        In:
            * queue: Queue to display.
        Out:
            * None.
    """

    # Shows the list
    print(queue)
import java.util.ArrayList;
import java.util.List;

public class ListQueue {
    private List<Object> queue;

    public ListQueue() {
        this.queue = new ArrayList<>();
    }

    public boolean isEmpty() {
        /**
         * This function checks if the queue is empty.
         * @return True if the queue is empty, False otherwise.
         */
        return this.queue.isEmpty();
    }

    public void push(Object item) {
        /**
         * This function adds an element to the queue.
         * The element is added at the beginning of the list.
         * @param item Element to add.
         */
        this.queue.add(0, item);
    }

    public Object pop() {
        /**
         * This function removes the last element of the queue.
         * @return The removed element.
         */
        if (this.queue.isEmpty()) {
            throw new IllegalStateException("Queue is empty");
        }
        return this.queue.remove(this.queue.size() - 1);
    }
}

3.2 — Use of doubly-linked lists

A doubly-link list can be used to implement a stack or a queue. Enqueuing creates a new element which is added to the beginning of the doubly-linked list, as with a stack. But dequeuing consists, in the case of a queue, in removing the element at its tail, whereas it is the element at its head in case of a stack.

The implementation of a queue using a doubly-linked list is left for the pratical activity.

4 — A practical use

The following is a toy example of a program that uses a queue to process a string.

​
# Ask for a string
s = input("Enter a string: ")

# Initialize a queue with the length of the string
my_queue = initialize()
for i in range(len(s)):
    push(my_queue, s[i])

# Process the elements one by one
result = ""
while not is_empty(my_queue):
    result += pop(my_queue)

# Show the result
print(f"Characters of {s} processed in order using a queue:")
display(result)
/**
 * Three elements processed in order using a queue
 **/
public static void main(String[] args) {
        ListQueue queue = new ListQueue();
        queue.push(1);
        queue.push(2);
        queue.push(3);
        System.out.println("Queue after pushes: " + queue.queue);
        System.out.println("Popped element: " + queue.pop());
        System.out.println("Queue after pop: " + queue.queue);
    }

To go further

Remember that all examples above are pedagogical, and made to understand how to create structures. For such simple structures, you should use default implementations.

For instance, it is more appropriate to use the Python deque class in package collections, which provides the optimal operations for enqueuing and dequeuing.

An exercice in the pratical activity will illustrate the efficiency gain when appropriate and optimized data structures are used.

To go beyond