Binary search tree

In brief

Article summary

We introduce the data structure called the “binary search tree” (BST). This data structure helps maintain an ordered dataset, supporting efficient operations such as insertion and searching for minimum values.

Key operations in a BST, such as finding the minimum value and inserting a new key while preserving the tree’s structure, are explained with algorithms and pseudocode.

Main takeaways

• A BST maintains order by placing smaller values to the left and larger values to the right of each node.

• Operations like finding the minimum or maximum are efficient because the tree structure reduces the number of comparisons.

• Insertion in a BST and searching for the minimum value both have a time complexity of $O(h)$, where $h$, is the height of the tree.

• BSTs are efficient when balanced, i.e., $h= O(log_2(n))$, though their performance can degrade if the tree is unbalanced.

Article contents

1 — Choosing a data structure

In the previous class, you explored different ways of storing data, such as arrays and linked lists. Depending on how you intend to use the data, certain operations can be performed more efficiently with specific data structures. Therefore, it’s important to choose a data structure that best suits your problem’s requirements. In this class, we will focus on binary search trees, a type of data structure that allows for efficient insertion of new data while maintaining the ability to quickly find minimum values within the dataset.

But why such problem is important? A simple application is the following:

You are in charge of scheduling machine learning (ML) jobs for a high-performance computing cluster. Different jobs have varying levels of urgency based on factors such as deadlines, computational requirements, and the impact of results. For instance, a job that fine-tunes a model for an urgent medical diagnosis application should probably get computational resources sooner than a batch job training a model for movie recommendations, regardless of submission time.

How do we always choose the most urgent ML job when new jobs continue to arrive?

From a computer scientist perspective, your problem is as follows:

Which data structure should you choose to easily add new jobs and quickly remove the most urgent job?

We could start with a list of size $N$. But what type of list?

1. Option 1 – Store jobs in a list:

   • Adding a new job is of order $O(N)$. Indeed, remember that an array is great for static operations, but not at all for dynamic operation. For instance, when adding or removing an element (and not replacing an element at a certain location), you are forced to reallocate the array and shifting all items after the modified item.
   • Remove min/max is done by searching in the entire list and therefore will be of order $O(N)$.

2. Option 2 – Store jobs in a sorted list:

   • Adding a new job is of order $O(N)$.
   • Remove a new job is of order $O(1)$

We are looking for a data structure where such operations are in $\Theta(log(N))$. A possible structure which can satisfied such properties is called a Binary Search Tree.

2 — Binary Search Tree (BST)

2.1 — Defining a BST

Let us start by giving the definition of a Binary tree:

A binary tree is a tree (a connected graph with no cycles) where each node has the following fields:

• An item with a key field.
• A reference to a parent node (which can be absent).
• A reference to a left child node (which can be absent).
• A reference to a right child node (which can be absent).

Let’s use the following notations in the rest of this article:

• x – The current node in the tree.
• x.key – The key associated to node x.
• x.left – The left child of node x.
• x.right – The right child of node x.
• NIL : a null value or a leaf node indicator, meaning that there is no child.

To understand better how a binary tree is working, you can have a look the library binarytree (see the documentation). Here is a sample of code to vizualize different trees:

# Needed imports
from binarytree import tree, bst, heap, build

# Create a tree using functions from library binarytree
my_tree = tree(height=3, is_perfect=False)
print(my_tree)

# Build the tree from some values
values = [1, 14, 10, 5, 7]
my_tree = build(values)
print(my_tree)

2.2 — The BST property

We say that a binary tree satisfies the binary search tree property if for every node:

• Keys in a node’s left subtree are less than the key stored at the node.
• Keys in the node’s right subtree are greater than the key stored at the node.

Examples of binary trees with binary search tree property or not:

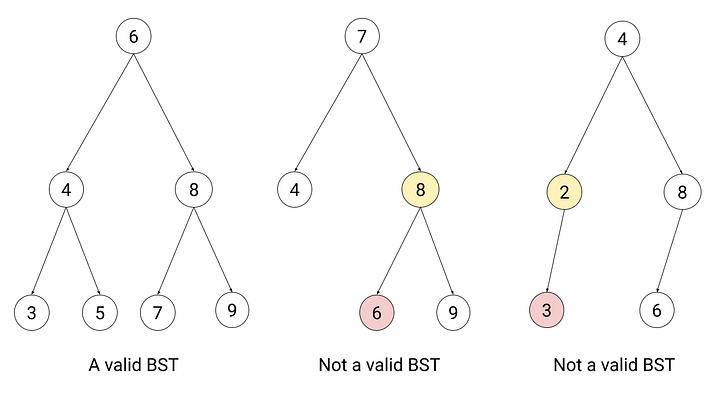
For more information, visit the source of the image.

2.3 — Operations on a BST

Returning to our problem, we will define algorithms to efficiently find the minimum or maximum and quickly insert or delete items in a binary search tree.

2.3.1 — Minimum

A efficient way of finding the node associated to the minimum key in a BST is simply done by following the left child from the root until we encoutner a NIL value. The pseudo-code is given below:

TREE-MINIMUM(x)
    while x.left ≠ NIL
        do x = x.left
    return x

Observe that if the binary search tree property is satisfied, then TREE-MINIMUM(x) is correct (meaning that the minimum is found).

The complexity of TREE-MINIMUM(x) is of order $O(h)$, where $h$ is the height of the tree.

You can think now on how to design TREE-MAXIMUM(x) which should return the node associated to the maximum key in a BST.

2.3.2 — Insertion in BST

When we want to insert a key in a BST, one of the main difficulty is that we have to maintain the binary search property. The classical approach is to insert the new key at a leaf. To decide after which leaf the new key should be added, the following iterative procedure can be followed:

• If the new key is less than the current node move to the left subtree.
• Otherwise, move to the right subtree.

To actually implement insertion in a BST, you can use recursion (you will see implementations in the practical) or for each node x, you will also need to define its parents x.p (the pseudo-code below uses this method).

You can find the pseudo-code below:

TREE-INSERT(T, z)
    x = T.root 
    y = NIL 
    while x ≠ NIL 
        y = x
        if z.key < x.key
            x = x.left
        else
            x = x.right
    z.p = y 
    if y == NIL
        T.root = z // tree T was empty
    elseif z.key < y.key
        y.left = z
    else
        y.right = z

In that pseudo-code, the variable x traces the path in the tree and y is the current parent of x. The while loop in lines 3–8 causes the two variables to move down the tree, going left or right depending on whether the key of z is bigger or smaller than the key of the current node x. If x is NIL then a leaf has been reached. This leaf is where the item ``_ is placed. Lines 9–15 set the variables to ensure that z is inserted in the right place in the tree.

TREE-INSERT(T, z) runs in $O(h)$, where $h$ is the height of the tree.

To go further

We said previously that most of the complexities of the different operations performed on a tree depend on its height. So it is important that, when we add an element, even if we want to conserve the binary search tree property, the height is not increasing linearly with the number of nodes.

You can try to see how the tree is looking like when you TREE-INSERT(T, z) on the list [1, 2, 3, 4, 5] and [3, 4, 1, 2, 5]. You will observe that the order in which you process the list will completly change the height of the tree.

In practice, we are interested in a tree having a length $O(log_2(n))$. Indeed $log_2(n)$ is the optimal lower bound on the height of a tree with $n$ nodes. Such tree are called balanced tree.

Balanced trees should have the following properties:

• For each node, the absolute difference between heights of left and right subtrees be less than 1.
• For each node, the left subtree (resp. right subtree) should be a balanced binary tree.

One simple solution to ensure that the tree is still balanced once we add an element is to “rotate” the tree to decrease the height of the tree. A rotation involves a pair of nodes $x$ and its parent $y$. If $x$ is initially the left child of $y$, then after the rotation $y$ is the right child of $x$.

You can find an example in the image below: For more information, visit the source of the image.

You can find the pseudo-code below for LEFT-ROTATE:

LEFT-ROTATE(T, x)
    y = x.right
    x.right = y.left 
    if y.left ≠ T.nil 
        y.left.p = x 
    y.p = x.p 
    if x.p == T.nil 
        T.root = y 
    elseif x == x.p.left 
        x.p.left = y 
    else
        x.p.right = y 
    y.left = x         
    x.p = y

Note that one of the nice property of the rotation is that the BST property is still satisfied after the rotation.

Now you can implement the functions LEFT-ROTATE(T, x) and RIGHT-ROTATE(T, x) and try to see how to make sure that the height of the tree is not too big! In practice, when you always want to have a balanced tree, you need to carefully use the LEFT-ROTATE(T, x) and _RIGHT-ROTATE(T, x) when adding or supressing an element. Different approaches lead to different balanced search tree such as:

The different pseudo-codes shown in this part of the course can be found in chapter 12 and 13 of the book Introduction to Algorithms, Fourth Edition.

To go beyond

• Red-Black Trees.

  Another data structure based on trees.

• AVL Trees.

  A balanced tree with additional constraints.