Divide and conquer
Reading time20 minIn brief
Article summary
This article explores the divide-and-conquer strategy in computer science, tracing its historical roots and explaining its application in algorithm design. It outlines the three main steps: divide, conquer, and combine, and discusses the inefficiencies that arise with overlapping subproblems.
The article also introduces memoization and dynamic programming as techniques to optimize recursive algorithms, using the Fibonacci sequence as a case study. It also covers optimization problems and the change-making problem, demonstrating how dynamic programming and greedy algorithms can be applied. The article concludes with a comparison of these approaches and their trade-offs.
Main takeaways
-
The divide-and-conquer strategy involves dividing a problem into smaller subproblems, solving them independently, and then combining their solutions to solve the original problem.
-
Memoization and dynamic programming techniques can optimize recursive algorithms by avoiding redundant computations of overlapping subproblems.
-
Dynamic programming ensures optimal solutions by considering all possibilities of solutions.
-
Choosing the right algorithmic approach (recursive, memoized, or dynamic programming) based on the problem’s characteristics is essential for efficient problem-solving.
Article contents
1 — Divide and conquer
The maxim “Divide and Conquer” has taken very different guises over time and been used in many political occasions before being used in computer science. Its origin may be attributed to Philip II of Macedon, as “Διαίρει καὶ βασίλευε” (Diaírei kaì basíleue) in Greek, literally “divide and reign”. Whether in politics or science, it is indeed easier to master a complex problem when it can be divided in smaller, simpler, subproblems.
Algorithmically solving a problem using a divide-and-conquer strategy requires three steps:
- Divide – The problem is divided (or decomposed) into smaller subproblems.
- Conquer – Each of the subproblems is solved independently.
- Combine: The subproblem solutions are combined (or composed) to produce the solution to the initial problem.
The Conquer step may require in turn to apply a specific divide-and-conquer strategy, because the subproblems are of another nature than the initial problem. When looking at basic problems, the subproblems are however typically of the same nature as the initial one, only smaller (this could actually be used as a definition of a basic problem). Such problems can be defined recursively and directly implemented as recursive functions. You have previously seen some examples of such problems with their recursive implementation in session 2.
In this course, we are going to consider specific cases where the same (sub)problem instances occur several times when solving a given problem instance. The initial problem is said to have overlapping subproblems. In such a case, a direct implementation of the recursive definition of the problem can be terribly inefficient as the same subproblem instances are solved again and again.
There are two basic techniques to avoid this redundancy: memoization and dynamic programming. We are going to see how these techniques apply to single-solution problems, that is problems that are neither search problems nor optimization problems (see the article on problems).
In the literature, the term “divide-and-conquer” is sometimes only used when the subproblems are non-overlapping.
2 — Single-solution problems
2.1 — The Fibonacci numbers
Let us explain the principle of problem decomposition by looking at the the Fibonacci numbers. This sequence was already used very early by Indian mathematicians as a way to enumerate patterns of Sanskrit poetry. It owes its name to the Italian mathematician Leonardo of Pisa, later called Fibonacci, who introduced the sequence in his Book of Calculation (1202). The Fibonacci number $F_n$ gives, at the end of month $n$, the size of an idealized rabbit population that behaves as follows:
- Initially, a first breeding pair of rabbits is put in a field.
- A breeding pair of rabbits mates when they are one-month old and produces a new pair of rabbits a month later. Once they are mature, they do so each month.
Here is an illustration of how the population evolves over the first six months:
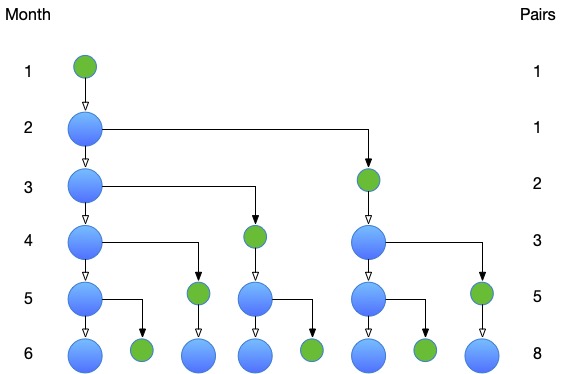
At the end of the first month, there is only one breeding pair, $F_1 = 1$. At the end of the second month, there is still one breeding pair, $F_2 = 1$, but this breeding pair is mature, and has produced, by the end of the third month, a new breeding pair, $F_3 = 2$.
More generally, at the end of month $n$, there are the breeding pairs that were there at the end of the previous month, as well as the new breeding pairs produced by the mature pairs, that is, the breeding pairs that were there two months before. This gives $F_n = F_{n-1} + F_{n-2}$. The sequence can be completed with $F_0 = 0$, in which case $F_n = F_{n-1} + F_{n-2}$ is already true for $n = 2$.
To sum up, the Fibonacci numbers may be defined by the recurrence relation: $F_0 = 0$, $F_1 = 1$, and $F_n = F_{n-1} + F_{n-2}$.
2.2 — The recursive version
This can easily be implemented in Python:
# Required to measure the time taken by the program
import time
from typing import Callable
def fib (n: int) -> int:
"""
The Fibonacci numbers are defined by the recurrence relation F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}.
This function computes F_n.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Base cases
if n == 0:
return 0
if n == 1:
return 1
# Recursive case
return fib(n - 1) + fib(n - 2)
def time_call (f: Callable, n: int) -> None:
"""
This function measures the time taken by the function f to compute f(n) and prints the result.
In:
* f: A function to measure.
* n: An integer.
Out:
None
"""
start = time.perf_counter()
print(f'{f.__name__}({n}) = {f(n)}')
elapsed = time.perf_counter() - start
print(f'Time taken: {elapsed:.6f} seconds')
# Test cases
time_call(fib, 10) # 55
time_call(fib, 20) # 6765
time_call(fib, 40) # 832040import java.util.function.IntFunction;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
}
}Unfortunately, the complexity of the program is exponential in time.
This can be seen experimentally by timing the program (with the function time_call in the illustration) as well as theoretically by computing the running time $T(n)$ of the program:
Noting that:
$$T(n) \geq T(n-1) + T(n-2) \geq 2T(n-2) \geq 2^n(n-4) \geq ... \geq 2^{n/2} T(0) = 2^{n/2}$$In practice, drawing the call tree of, for instance, fib(5) shows that each call is actually repeated a growing number of times as the size of the subproblem decreases:
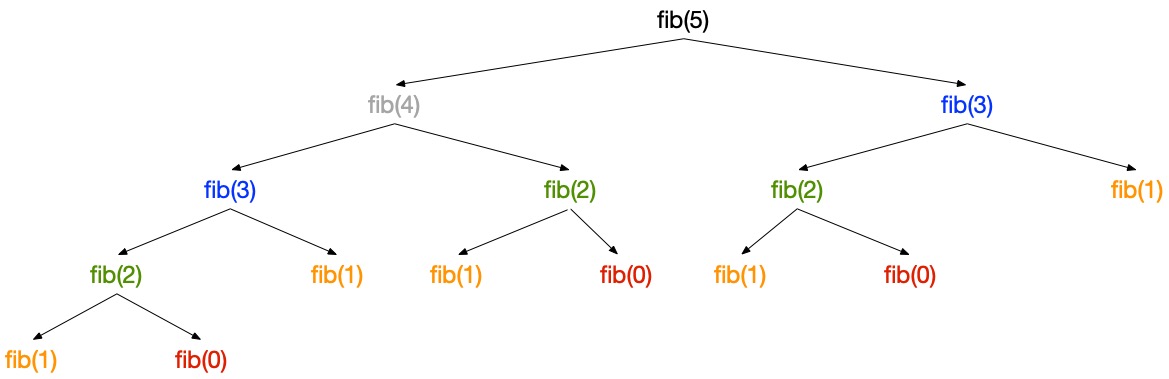
The call tree also gives the intuition that the program is linear in space. Each call pushes an activation record on the call stack and pops it when it returns. The maximum size of the stack corresponds to the maximum depth of the call tree. A call to $fib(n)$ pushes at most $n$ activation records on the stack.
A full study of the complexity of fib would require to look at the complexity of adding big integers, which does not take a constant time.
2.3 — The memoized version
The observation that almost all calls are repeatedly computed lead to the idea of memoization. What about building a memo (hence the term memoization) recording the results of the encountered calls in order to reuse them later?
A memo for a function $f$ of type $E \rightarrow S$ can be implemented as a dictionary of pairs $(key, value)$, where $key$ is an element of $E$ and $value$ is simply equal to $f(key)$. When a call $f(e)$ is encountered, either $e$ is a key in the dictionary and the corresponding value is returned, or there is no such key, $f(e)$ is computed, $(e, f(e))$ is added to the dictionary, and $f(e)$ is returned. Note that if $f$ has several parameters, i.e., $E$ has the form $E_1 \times...\times E_n$, then the keys are tuples of parameters.
In the case of Fibonacci, the parameter is an integer, it is possible to reduce the dictionay to an array, which has to be initialized with an invalid value (for instance -1), making it possible to tell between already computed values and still-to-be-computed values.
Here is the corresponding implementation in Python:
def fib_memo (n):
"""
This function computes the n-th Fibonacci number using memoization.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Initialization of memo
memo = [-1 for _ in range(n + 1)]
# Inner auxiliary function to recursively define Fibonacci and hide memoization from the user
def __fib_memo (n):
"""
This function computes recursively the n-th Fibonacci number using memoization.
In:
* n: an integer.
Out:
* The n-th Fibonacci number.
"""
# If the result has already been computed, return it
if memo[n] != -1:
return memo[n]
# Otherwise, standard computation (see earlier)
if n == 0:
result = 0
elif n == 1:
result = 1
else:
result = __fib_memo(n - 1) + __fib_memo(n - 2)
# Record the result in memo
memo[n] = result
return result
# Call the inner function
return __fib_memo(n)
# Test cases
time_call(fib_memo, 10) # 55 # cold start
time_call(fib_memo, 10) # 55 # warm start
time_call(fib_memo, 20) # 6765
time_call(fib_memo, 40) # 832040
time_call(fib_memo, 80) # 23416728348467685
time_call(fib_memo, 160) # 47108659444709974473273497672572071429
time_call(fib_memo, 320) # ...import java.util.function.IntFunction;
import java.util.Arrays;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static int fibMemo(int n) {
int[] memo = new int[n + 1];
Arrays.fill(memo, -1);
return fibMemoAux(n, memo);
}
private static int fibMemoAux(int n, int[] memo) {
if (memo[n] != -1) {
return memo[n];
}
if (n == 0) {
memo[n] = 0;
} else if (n == 1) {
memo[n] = 1;
} else {
memo[n] = fibMemoAux(n - 1, memo) + fibMemoAux(n - 2, memo);
}
return memo[n];
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
System.out.println("fibo memo");
// Test cases
timeCall(FibboInit::fibMemo, 10); // 55 # cold start
timeCall(FibboInit::fibMemo, 10); // 55 # warm start
timeCall(FibboInit::fibMemo, 20); // 6765
timeCall(FibboInit::fibMemo, 40); // 832040
timeCall(FibboInit::fibMemo, 80); // 23416728348467685
timeCall(FibboInit::fibMemo, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibMemo, 320); // ...
}
}Here memo is defined as local to the function fibo.
It could also be defined as a global variable in order to be shared through different calls to fibo.
When using an array for memoization, the size of the array must be known in advance. This can be problematic if the maximum size of the input is not known or if the input size can vary significantly. In addition, arrays are less flexible compared to other data structures like dictionaries. For example, if the input domain is sparse or non-contiguous, using an array can lead to wasted space. Dictionaries, on the other hand, can dynamically grow and only use memory for the keys that are actually needed.
The time complexity of the program is now linear. There is however a time-space trade-off: more space is used. In the case of Fibonacci, this additional space, at least when using an array, is proportional to the argument. The space complexity is therefore unchanged.
In general, when the recursive version of a problem takes exponential time, the dynamic programming version takes polynomial time, but this requires that the number of distinct subproblems is polynomial with respect to the problem size.
2.4 — Dynamic programming
When using either recursion or memoization, the execution proceeds in a top-down manner: starting from the problem with the biggest size, it solves subproblems of smaller sizes in order to finally solve the initial problem. But it is also possible to proceed the other way around, i.e., bottom-up.
The notion of problem size is key. It makes it possible to sort the problems with respect to their size. If solving a problem only relies on solving smaller subproblems, it is then possible to solve problems starting from their smaller subproblems (at any depth) and proceeding with bigger problems until the initial problem is solved.
All along the solutions are memoized, i.e., recorded in a memo. When a problem is about to be solved, all its subproblems have therefore already been solved by design.
When applied to fib$(n)$, the smallest problems, fib(0) and fib(1) are (trivially) solved first, and the computation proceeds with fib(2), fib(3)… until fib$(n)$ is reached.
Why is it called dynamic programming? Well, this has not much to do with programming (in Python or any other programming language), but rather relates to planning (building plans) and this planning is not dynamic (it does not happen when the program runs) but static (it is when we program that we do the planning). (see the Wikipedia article on dynamic programming).
Sometimes, memoization is classified as top-down dynamic programming.
2.4.1 — The subproblem graph
Solving a problem using dynamic programming requires to understand how the problem is structured in terms of its subproblems and their dependencies. This is represented by the subproblem graph, more precisely a directed acyclic graph. Each vertex corresponds to a problem with edges pointing to problems it directly depends on (they are subproblems, not subsub…problems). This corresponds to a kind of “compacted” version of the call tree of the recursive version, whereall the nodes with the same labels are merged.
Here is how the problem graph looks like for fib(5):
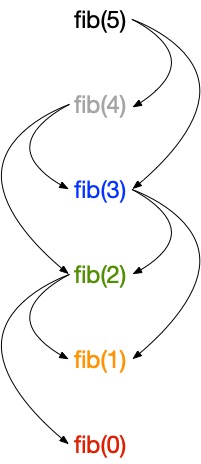
Sorting the vertices using a reverse topological sort gives the order in which the subproblems should be solved.
Basically, a vertex is selected only if the vertices it depends on have already been selected.
In terms of problems and subproblems, this corresponds to the idea that a problem can only be solved if its (direct) subproblems have already been solved.
In the case of fib, the computation should start from fib(0), then fib(1), fib(2)… fib($n$) for any $n$.
The graph can be used to determine the running time of the algorithm.
Since each subproblem is solved only once, the total cost is the sum of the times needed to solve each subproblem.
The time to compute a subproblem is typically proportional to the degree (the number of outgoing edges) of the corresponding vertex.
Assuming the degree does not vary with the size of the problem, the running time of an algorithm using dynamic programming is typically linear in the number of vertices and edges.
In the case of fib$(n)$, there are exactly $n$ vertices.
The running time is linear in $n$.
2.4.2 — The program
Now that we understand how to “plan” the computations, we can write a program computing the Fibonacci numbers with dynamic programming:
def fib_dp (n):
"""
This function computes the n-th Fibonacci number using dynamic programming.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Initialization of memo
memo = [0 for _ in range(n + 1)]
memo[1] = 1
# Exploit previous memoized results
# i.e., i in [2, n+1[ (or [2, n])
for i in range(2, n + 1):
memo[i] = memo[i - 1] + memo[i - 2]
return memo[n]
# Test cases
time_call(fib_dp, 10) # 55 # cold start
time_call(fib_dp, 10) # 55 # warm start
time_call(fib_dp, 20) # 6765
time_call(fib_dp, 40) # 832040
time_call(fib_dp, 80) # 23416728348467685
time_call(fib_dp, 160) # 47108659444709974473273497672572071429
time_call(fib_dp, 320) #import java.util.function.IntFunction;
import java.util.Arrays;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static int fibMemo(int n) {
int[] memo = new int[n + 1];
Arrays.fill(memo, -1);
return fibMemoAux(n, memo);
}
private static int fibMemoAux(int n, int[] memo) {
if (memo[n] != -1) {
return memo[n];
}
if (n == 0) {
memo[n] = 0;
} else if (n == 1) {
memo[n] = 1;
} else {
memo[n] = fibMemoAux(n - 1, memo) + fibMemoAux(n - 2, memo);
}
return memo[n];
}
public static int fibDp(int n) {
int[] memo = new int[n + 1];
memo[1] = 1;
for (int i = 2; i <= n; i++) {
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
System.out.println("fibo memo");
// Test cases
timeCall(FibboInit::fibMemo, 10); // 55 # cold start
timeCall(FibboInit::fibMemo, 10); // 55 # warm start
timeCall(FibboInit::fibMemo, 20); // 6765
timeCall(FibboInit::fibMemo, 40); // 832040
timeCall(FibboInit::fibMemo, 80); // 23416728348467685
timeCall(FibboInit::fibMemo, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibMemo, 320); // ...
System.out.println("dynamic programming");
// Test cases
timeCall(FibboInit::fibDp, 10); // 55 # cold start
timeCall(FibboInit::fibDp, 10); // 55 # warm start
timeCall(FibboInit::fibDp, 20); // 6765
timeCall(FibboInit::fibDp, 40); // 832040
timeCall(FibboInit::fibDp, 80); // 23416728348467685
timeCall(FibboInit::fibDp, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibDp, 320); // ...
}
}2.5 — Let us step back
You can check experimentally that the version using dynamic programming runs faster than the version using memoization.
It also uses less memory (memo uses the same amount of heap memory in both versions and the stack is used for a single activation record corresponding to the initial call).
However, we have gained much more between the initial version and the memoized version (from exponential to linear complexity) than between the memoized version and the dynamic programming version (a constant factor).
Also, the dynamic programming version requires more work and is more prone to errors.
There is a bigger gap between the specification of the problem and the programming of its solution.
As a result, it is often a good idea to go through all the steps, that is, produce the recursive version, the memoized version, and finally the dynamic programming version, only if the memoized version is not efficient enough. In case the dynamic programming version is required, the memoized version is still useful to efficiently test the correction of the dynamic programming version.
To go further
Looks like this section is empty!
Anything you would have liked to see here? Let us know on the Discord server! Maybe we can add it quickly. Otherwise, it will help us improve the course for next year!
To go beyond
- Bellman equation.
Dynamic programming relies on a theoretical principle studied by Richard Bellman that relates to an equation between the optimal solution of a problem and a combination of optimal solutions for some of its subproblems. For the most curious of you, have a look to this theoretical background.