Session pratique

Présentation & objectifs

Dans cette session, vous allez concevoir un système robuste d’analyse de données issues d’un capteur de température. Votre application ne doit jamais s’arrêter sur une erreur, même en cas :

• de données corrompues,
• de valeurs aberrantes,
• de panne du capteur.

Il vous faudra donc gérer les situations imprévues et les erreurs d’exécution du programme pour assurer la continuité du service.

De plus, votre application doit pouvoir être facilement étendue avec d’autres fonctionnalités.

Pour répondre à ces exigences, vous veillerez à :

• appliquer les principes de la programmation défensive,
• tester les fonctionnalités de votre code,
• documenter et commenter votre code pour faciliter son utilisation et sa complétion,
• respecter les conventions de codage pour partager du code de qualité.

Organisation et préparation de l’activité pratique

Vous allez réaliser cette activité à deux (et maximum un trinôme dans le groupe si nécessaire). Les développeurs étant désignés dans le reste du document en tant qu’étudiant1 et étudiant2.

L’activité est découpée en deux parties donnant lieu à deux programmes ; un capteur de données numériques qui écrit les données dans un fichier et un lecteur/analyseur des données produites par le capteur.

Environnement collaboratif

À deux, commencez par faire un fork du dépôt prog_session2_sensor en tant qu’étudiant1 sur gitlab-df.imt-atlantique.fr. Ajoutez ensuite étudiant2 pour qu’il y ait également accès en tant que developer.

En cas de travail en trinôme, deux étudiants collaborent sur l’écriture du même programme.

Le dépôt cloné a la structure de fichiers suivante :

• README.md à compléter avec une description au format markdown du programme et de la composition de l’équipe de développeurs,
• un répertoire src avec deux sous-répertoires sensor et reader. Ces répertoires contiennent des fichiers de tests unitaires nommés respectivement tests_sensor.py, tests_reader.py et tests_analyzer.py,
• un répertoire doc avec deux sous-répertoires sensor et reader.

Versionnez fréquemment votre code avec des messages de commit explicites.

Aides techniques en Python

Lecture/écriture dans un fichier

Pour manipuler un fichier de votre système depuis votre code Python, il faut disposer d’un lien vers le fichier, lien que l’on appelle un descripteur et qui est de type TextIOWrapper.

L’obtention d’un descripteur s’effectue à l’aide de la fonction open. Lorsque le fichier n’est plus utilisé, le descripteur doit être libéré en fermant le fichier avec la méthode close, ce qui permet également de s’assurer que toutes les données ont bien été écrites sur le fichier avant la fin du programme.

file_d = open("data.txt", 'r')
# use the file
file_d.close()

Il est cependant conseillé, pour ne pas oublier de fermer le lien ouvert vers le fichier, d’encapsuler l’utilisation du fichier par un bloc d’instruction with comme illustré ci-dessous :

 with open("data.txt", 'r') as file:
    # use the file
    # no need to close

À la fin du bloc with le descripteur file est automatiquement fermé.

L’argument r passé à la méthode open indique que le fichier est ouvert en mode lecture. Il peut être remplacé par w pour ouvrir le fichier en mode écriture, a pour ouvrir le fichier en mode ajout.

Bien que cette solution ne soit pas optimale, vous allez pour le moment ouvrir un lien vers le fichier à chaque tentative d’écriture ou de lecture.

Temporisation

L’écriture des températures relevées par le programme sensor dans le fichier data.txt ainsi que la lecture de ces données par le programme reader s’effectuent selon une certaine fréquence en secondes. Pour mettre en pause un programme x secondes, vous pouvez utiliser la fonction sleep du module time.

time.sleep(.7) # pauses the program 0.7 seconds

Pseudo-aléatoire

Vous aurez besoin de simuler de l’aléatoire à l’aide du module random. Voici ci-dessous des exemples pratiques pour retourner pseudo-aléatoirement une valeur de la liste passée en paramètre ou une valeur suivant une distribution gaussienne :

import random

l = ["ERR1", "ERR2", "ERR3"]

# returns True or False
if random.choice([True, False]):    
    # returns an indice between 0 and 2 included
    rand_n=random.choice(range(len(l))) 
    print(f"Random between 0 and {len(l)-1}: {rand_n}")
    print(f"Random element from list: {l[rand_n]}")
    # alternative way to get a random element
    # rand_n=random.choice(l)
    # print(f"Random element from list (alternative): {rand_n}")
else:
    mean=10
    std=3
    # returns a float following the Gaussian distribution set with mean and std
    rand_f=random.gauss(mean,std)
    print(f"Random wrt. Gaussian distribution (mean={mean}, std={std}): {rand_f}")

Gestion des logs

La classe Analyzer va générer des logs avec les statistiques calculées. Un moyen de générer ces messages est d’utiliser le module logging de python. Le code ci-dessous montre comment générer des logs sur la sortie standard :

import logging

# creation and configuration of the logger
logging.basicConfig(level=logging.DEBUG) # Publish logs from the DEBUG level
logger = logging.getLogger(__name__) # get a logging instance

maxv=102.3
# use the logger to log the max value
logger.info(f"Max value recorded: {maxv}")

Lorsqu’un niveau de log est défini, tous les messages de log de ce niveau et de niveaux supérieurs (i.e., plus sévères) seront publiés. Il existe plusieurs niveaux de log, chacun ayant un degré de sévérité différent. Les niveaux de log standard sont, par ordre croissant de sévérité : NOTSET, DEBUG, INFO, WARNING, ERROR et CRITICAL.

Un capteur et un lecteur

Le schéma ci-dessous illustre la structure du système logiciel à développer. Il est constitué de trois modules Python. Le premier définit une classe Sensor qui génère des valeurs numériques (des mesures de température d’un moteur à explosion par exemple), les mesures étant écrites dans un fichier (nommé data.txt par défaut). Le deuxième module définit une classe Reader qui lit les données du fichier et les envoie au troisième module qui analyse ces données et en fait des traces dans un fichier de log (nommé analyzer.log par défaut).

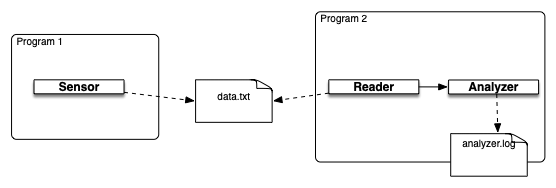
Chaque programme est décrit par un cahier des charges fonctionnelles associé à un ensemble de tests automatiques que vous allez utiliser pour vérifier son bon fonctionnement.

Au cours de cette première partie, l'étudiant1 travaille sur le programme 1 et l'étudiant2 sur le programme 2.

Les deux programmes doivent répondre à certaines exigences :

1. valider les tests unitaires fournis,
2. disposer d’une documentation en anglais générée par l’outil pydoc à partir des docstrings présentes dans le code,
3. contenir du code satisfaisant au maximum la PEP8 et comportant des commentaires utiles.

Programme 1: la classe Sensor (étudiant1)

Le développement du programme 1 s’effectue par étape.

Étape 1 : La classe Sensor et ses attributs

Implémentez une classe nommée Sensor (dans un fichier de chemin src/sensor/sensor.py) qui simule le comportement d’un capteur de données :

• qui capte des valeurs selon une loi Gaussienne donnée par sa moyenne et sa déviation standard,
• qui tombe en panne toutes les 10 captations de données en moyenne.

Toute instance de cette classe possède les attributs suivants :

__id : str # sensor identifier (its name)
__mean : float # Gaussian mean
__std : float # standard deviation of the Gaussian distribution
__sleep_time : float # time in seconds between two produced values
__storage_file_name : str # name of the file where the sensor stores data

Le constructeur de la classe permet de spécifier les valeurs de chacun de ces attributs ou de leur affecter les valeurs par défaut suivantes :

__id = "sensor"
__mean = 90.0
__std = 5.0
__sleep_time = 3.0
__storage_file_name = "../data.txt"

Chaque attribut doit être accessible via une méthode de type accesseur (getter) dont les prototypes sont les suivants :

def get_id(self) -> str:

def get_mean(self) -> float:

def get_std(self) -> float:

def get_sleep_time(self) -> float:

def get_storage_file_name(self) -> str:

Une fois le constructeur et les accesseurs définis, exécutez les tests associés avec les commandes suivantes (à exécuter depuis le répertoire src/sensor) :

python tests_sensor.py TestSensor.test_encapsulation_default_values python tests_sensor.py TestSensor.test_encapsulation_custom_values

Étape 2 : Fonctionnalités du capteur

Vous allez désormais implémenter les fonctionnalités du capteur qui sont les suivantes :

1. Génération d’une donnée selon une loi gaussienne paramétrée par les attributs __mean et __std. Le prototype de la méthode est donné ci-dessous :

   def get_value(self) -> float:

   La valeur générée par la méthode get_value(self) doit être comprise entre 0 et 150 ou une exception de type OutofBoundsException (classe d’exception existante dans le fichier sensor.py). Une captation sur 10 en moyenne, une panne est simulée et le capteur retourne une exception de type NotRespondingException (classe d’exception présente dans sensor.py). Cette méthode doit être testée à l’aide du test suivant :

   python tests_sensor.py TestSensor.test_get_value

2. Mise en place du capteur. La méthode run simule la captation de données et leur stockage dans le fichier __storage_file_name. Le prototype de la méthode est donné ci-dessous :

    def run(self) -> None:

   La méthode implémente une boucle infinie dans laquelle :

   1. le descripteur du fichier utilisé pour le stockage de données est ouvert en écriture
   2. au premier pas de la boucle, le capteur ajoute quatre lignes commençant par # ayant la forme suivante :

   #Initial content
   #Sensor ID:<ID>
   #Sleep Time:<TIME>
   #Storage File:<FILE_NAME>

   où <ID> est l’ID du capteur, <TIME> le temps d’attente entre 2 données produites et <FILE_NAME> le nom du fichier où les données sont stockées

   3. une valeur est générée
   4. une écriture dans le fichier est produite qui est soit la valeur générée, soit OoB en cas d’exception OutofBoundsException, soit NR en cas d’exception NotRespondingException.

   En outre, trois types d’exception doivent être gérées par cette méthode : KeyboardInterrupt pour arrêter l’exécution avec un Ctrl-C par exemple, IOError en cas d’impossibilité d’ouvrir ou d’écrire dans le fichier de données et Exception pour toute autre exception.

   Veillez à ouvrir un nouveau descripteur vers le fichier à chaque tour de boucle. Ce n’est pas idéal, mais simple. Si le temps le permet, vous verrez en complément comment faire communiquer des programmes de manière plus habile.

Une fois la classe implémentée, exécutez tous les tests unitaires fournis avec la commande suivante (ou directement depuis VSCode) : python tests_sensor.py

Étape 3 : Vers un code plus exploitable

Avant de partager votre code, effectuez les vérifications suivantes :

• votre code respecte au maximum les conventions de codage de la PEP8. Pour ce faire, appliquez la commande suivante et tentez de vous rapprocher d’un score de 10/10 : pylint sensor.py
• ajoutez des commentaires à votre code pour rendre son déroulement plus explicite
• ajoutez des documentations (sous forme de docstring) au module, aux classes et à leurs méthodes. Puis, générez une documentation à l’aide de la commande suivante : pydoc -w sensor et déplacez la documentation dans le répertoire doc/sensor/.

Une fois votre code complété, pushez vos modifications sur votre dépôt dans gitlab-df.imt-atlantique.fr. Passez à la partie Evaluation par les pairs ou aidez votre binôme à développer son programme.

Programme 2 (étudiant2)

Le développement du programme 2 s’effectue par étapes avec le développement de deux classes.

Étape 1 : La classe Analyzer et ses attributs

Implémentez une classe nommée Analyzer (dans un fichier de chemin src/reader/analyzer.py). Cette classe analyse les __buffer_size dernières données générées par un capteur de données et trace le résultat dans un fichier de log.

Toute instance de cette classe possède les attributs suivants :

__buffer_size : int # number of values to retrieve before performing an analysis 
__values : list[float] # list of the __buffer_size last values generated by the sensor
__errors : list[str] # list of errors generated by the sensor since the last analysis
__logger : logging.Logger # the logger used by the analyzer
__log_file : str # name of the log file

Le constructeur de la classe permet de spécifier le nombre de données à traiter lors de chaque analyse (__buffer_size avec comme valeur par défaut 10) et le nom du fichier recevant les logs (__log_file initialisé par défaut à analyzer.log). La configuration du gestionnaire de logs ainsi que l’initialisation des autres attributs sont réalisées comme suit :

self.__values : list[float] = []
self.__errors : list[str] = []
self.__logger : logging.Logger = logging.getLogger(__name__) # get a logging instance
self.__logger.setLevel(logging.DEBUG) # set the logging level
self.__logger.addHandler(logging.FileHandler(self.__log_file)) #add a file handler to the logger

Certains attributs doivent être accessibles via une méthode de type accesseur (getter) dont les prototypes sont les suivants :

def get_values(self) -> list[float]:
        
def get_errors(self) -> list[str]:

def get_buffer_size(self) -> int:

def get_logger(self) -> logging.Logger:

Les autres attributs n’ont pas de raison d’être accessibles depuis l’extérieur de la classe. Dans un autre langage de programmation, on les aurait déclarées comme privées.

Une fois le constructeur et les accesseurs définis, exécutez les tests associés avec les commandes suivantes (à exécuter depuis le répertoire src/reader) : python tests_analyzer.py TestAnalyzer.test_encapsulation_default_values python tests_analyzer.py TestAnalyzer.test_encapsulation_custom_values

Étape 2 : Fonctionnalités de la classe Analyzer

Vous allez désormais implémenter les fonctionnalités d’analyse (très simples) de valeurs. Il y en a deux :

1. ajout d’une donnée dans le fichier de log. Si c’est une valeur pouvant être convertie en réel, elle est ajoutée dans la liste __values et le message Added value:<VALUE> où <VALUE> est la valeur ajoutée dans le fichier de log (comme un message de débogage). Sinon la valeur est ajoutée dans la liste __errors et le message Error adding value:<VALUE> où <VALUE> est la valeur ajoutée dans le fichier de log (comme une erreur). Cette méthode déclenche également l’analyse (voir méthode suivante) dès que self.__buffer_size nouvelles valeurs ont été enregistrées dans __values. Le prototype de cette méthode est le suivant :

   def add_data(self, value: str) -> None:

2. génération du résultat de l’analyse à savoir la moyenne, le minimum et le maximum des self.__buffer_size dernières valeurs générées par le capteur (et présentes dans la liste __values).

   def log_analysis(self) -> None:

Une fois la classe implémentée, vous pouvez exécuter tous les tests unitaires avec la commande suivante ou directement depuis VSCode: python tests_analyzer.py

Étape 3 : Vers un code plus exploitable

Avant de partager votre code, effectuez les vérifications suivantes :

• votre code respecte au maximum les conventions de codage de la PEP8, pour se faire, appliquer la commande suivante et tentez de vous rapprocher d’un score de 10/10 : pylint analyzer.py
• ajoutez des commentaires à votre code pour rendre son déroulement plus explicite
• ajoutez des documentations (sous forme de docstring) au module, la classe et ses méthodes. Puis, générez une documentation à l’aide de la commande suivante : pydoc -w analyzer et déplacez la documentation dans le répertoire doc/reader/.

Étape 4 : La classe Reader et ses attributs

Implémentez une classe nommée Reader (dans un fichier de chemin src/reader/reader.py). Elle lit les données produites par le capteur et stockées dans un fichier et les envoie à l’Analyzer pour analyse.

Toute instance de cette classe possède les attributs suivants :

__analyzer : Analyzer # the analyzer associated to the reader
__sleep_time : float # time in seconds between two data readings 
__file_name : str # the name of the file where data have been stored by the sensor

Le constructeur de la classe permet de spécifier l’instance d’analyseur associé, le temps d’attente entre 2 lectures (__sleep_time avec comme valeur par défaut 1.0) et le chemin du fichier dans lequel lire (__file_name avec comme valeur par défaut ../data.txt).

Tous les attributs doivent être accessibles via une méthode de type accesseur (getter) dont les prototypes sont les suivants :

def get_analyzer(self) -> Analyzer:
        
def get_sleep_time(self) -> float:

def get_file_name(self) -> str:

Une fois le constructeur et les accesseurs définis, exécutez les tests associés avec les commandes suivantes (à exécuter depuis le répertoire src/reader) : python tests_reader.py TestReader.test_encapsulation_default_values python tests_reader.py TestReader.test_encapsulation_custom_values

Étape 5 : Fonctionnalités de la classe Reader

Vous allez désormais implémenter les deux fonctionnalités de la classe Reader:

1. une méthode prenant en paramètre une ligne lue depuis le fichier des données. Les lignes commençant par un # sont ignorées, les autres sont envoyées à l’analyseur. Le prototype de cette fonction est le suivant :

   def process_line(self, line: str) -> None:

2. une méthode principale qui met en place la lecture continue sur le fichier de données. Après l’ouverture du fichier de données en lecture, la méthode entre dans une boucle infinie et tente de lire une ligne. S’il y en a une, elle la traite avec la méthode précédente, sinon le programme est mis en pause pendant une durée de self.__sleep_time secondes. Le prototype de cette fonction est le suivant :

   def run(self) -> None:

   Plusieurs types d’exception doivent être gérées séparément dans cette méthode run :

   • KeyboardInterrupt pour arrêter avec un Ctrl-C par exemple,
   • FileNotFoundError lorsque le fichier de données n’existe pas,
   • IOError pour une erreur de lecture du fichier,
   • Exception pour tout autre raison d’échec.

   Le premier type d’exception entraîne la fin du programme. Pour les autres, un message d’erreur est affiché, puis la méthode run est exécutée de nouveau après un temps de pause correspondant à deux fois le temps d’attente.

Une fois la classe implémentée, vous pouvez exécuter tous les tests unitaires avec la commande suivante ou bien directement depuis VSCode : python tests_reader.py

Étape 6 : Vers un code plus exploitable

Avant de partager votre code, effectuez les vérifications suivantes :

• votre code respecte au maximum les conventions de codage de la PEP8, pour se faire, appliquer la commande suivante et tentez de vous rapprocher d’un score de 10/10 : pylint reader.py
• ajoutez des commentaires à votre code pour rendre son déroulement plus explicite
• ajoutez des documentations (sous forme de docstring) au module, la classe et ses méthodes. Puis, générez une documentation à l’aide de la commande suivante : pydoc -w reader et déplacez la documentation dans le répertoire doc/reader/.

Evaluation par les pairs

Vous avez développé les deux programmes en parallèle. Maintenant, chaque étudiant doit récupérer sur sa machine la dernière version du code poussé sur le dépôt Git.

Retour qualitatif

Chaque étudiant va désormais analyser le livrable de son binôme et le questionner sur ses choix en matière de :

• programmation défensive (Toutes les erreurs d’exécution possibles ont-elles été gérées ? La gestion de ces erreurs d’exécution est-elle conforme au cahier des charges ? etc.),
• commentaires et documentation (Les commentaires et la documentation sont-ils d’un niveau de détail suffisant pour comprendre le code sans avoir à l’analyser ?)
• qualité du code (Les conventions de codage ont-elles été respectées ?).

Test

Chaque étudiant va exécuter le code du capteur sensor.py et le code du lecteur reader.py dans un terminal dédié. Pour ce faire, ajouter le code suivant dans le fichier reader.py :

if __name__=="__main__":
    a = Analyzer()
    r = Reader(a)
    r.run()

et le code suivant dans le fichier sensor.py :

if __name__=="__main__":
    s = Sensor()
    s.run()

Logiquement, vous devez pouvoir exécuter ces deux programmes dans n’importe quel ordre. Le capteur doit pouvoir être arrêté et ré-exécuté sans que le lecteur ne s’arrête.

Si vous n’arrivez pas à atteindre ce niveau de fonctionnalité, analysez à deux le code pour effectuer les corrections nécessaires. Profitez-en pour discuter avec votre collaborateur de ses choix d’implémentation.

Pour aller plus loin

Plusieurs capteurs et un analyseur

L’objectif de cette seconde partie est double :

1. continuer à faire un retour à votre collaborateur sur la qualité de son livrable,
2. compléter les fonctionnalités de l’application en gérant plusieurs types de capteurs et un système d’analyse par capteur.

Pour cette seconde partie, vous allez inverser les rôles. étudiant2 va compléter le programme 1 sur les capteurs et étudiant1 va compléter le programme 2 sur les analyseurs.

Lors de ce travail d’implémentation, discutez avec votre collaborateur :

• des éventuels manques ou imprécisions dans la documentation et les commentaires,
• des choix d’implémentation ou de nommage que vous désapprouvez. Vous pouvez invoquer pylint sur le code de votre collaborateur pour identifier puis discuter des violations de la PEP8.

Complétion du programme 1 (étudiant2)

Définissez un second type de capteur, dont l’objectif est d’effectuer un test de bon fonctionnement. Ce capteur retourne un booléen au lieu d’un réel. Un capteur a donc une propriété supplémentaire qui indique son type : binary ou continue. Étant donné que plusieurs capteurs écriront dans un même fichier, chaque écriture sera préfixée par le nom du capteur et son type. Considérons deux capteurs nommés sensor1 de type binaire et sensor2 de type continu, on pourra alors trouver dans le fichier de données les captations suivantes :

sensor1:BinarySensor:1
sensor1:BinarySensor:1
sensor2:ContinuousSensor:12.255
sensor1:BinarySensor:0
sensor2:ContinuousSensor:90.024
...

Commentez, documentez et validez la conformité de votre code vis-à-vis de la PEP8. Les tests unitaires de la partie 1 ne sont cependant pas adaptés à cette nouvelle version du code, il est donc inutile de tester votre code. Mais patience, dès la session prochaine, vous apprendrez à concevoir des tests unitaires. N’oubliez pas qu’un objectif de cette partie est de faire un retour à votre collaborateur, qui a développé la partie, sur la qualité de son livrable.

Complétion du programme 2 (étudiant1)

Pour le moment, le programme contient une instance de la classe Reader et une instance de la classe Analyzer. Vous allez désormais modifier la classe Reader pour qu’elle soit associée à plusieurs analyseurs.
Vous allez mettre en place deux nouveaux types d’analyseurs :

• un analyseur de captations binaires dont l’analyse vise à quantifier le pourcentage de tests réussis,
• un analyseur d’erreurs qui calcule le nombre et le pourcentage d’erreurs de chaque type par capteur. L’analyse des erreurs n’est pas déclenchée selon une certaine fréquence, mais effectuée lorsque le programme reader est arrêté.

Un analyseur doit désormais être associé à chaque capteur pour lequel une donnée est lue dans le fichier. Les analyseurs de valeurs (binaires ou continues) dirigent leurs analyses vers un même fichier, et l’analyseur d’erreur vers un fichier de log spécifique.

Mise en commun (étudiant1 et étudiant2)

Après avoir mis-à-jour le dépôt git sur le serveur gitlab, analysez la documentation et les messages de commit qui concernent les modifications effectuées par votre collaborateur sur son code afin de comprendre ses choix d’implémentation.

Échangez sur les modifications apportées au code par votre collaborateur pour prendre en compte les nouvelles fonctionnalités de la partie 2 et faites lui un retour sur la qualité de ce dernier livrable.

Puis, testez chacun l’exécution de plusieurs capteurs associés à un lecteur avec plusieurs analyseurs :

• définissez un programme par capteur (e.g. run_sensor1.py, run_sensor2.py, etc.) et exécutez ces programmes dans des terminaux différents,
• définissez un programme pour exécuter le lecteur.

Pour aller encore plus loin

Pour simuler l’indépendance des capteurs et du lecteur, vous avez exécuté les programmes depuis différents terminaux, chaque terminal étant isolé dans un processus système. Depuis un même programme Python, il est possible d’exécuter différents morceaux de code indépendants les uns des autres en utilisant des threads. Des thread sont également appelés processus légers et peuvent être exécutés dans un même processus mais en parallèle. Utilisez la documentation pour expérimenter ce parallélisme.

Faire communiquer deux programmes sur une même machine, vous verrez comment le faire en réseau en S6, n’est pas une chose aisée. Le recours à un fichier partagé tel que nous l’avons fait n’est vraiment pas l’idéal. De nombreuses tentatives de lecture occupent inutilement des ressources de calcul. Une méthode plus appropriée est d’avoir recours aux techniques de communication entre processus (Inter Process Communication). Vous pouvez consulter la documentation des IPC en Python pour voir notamment comment des techniques d’envoi de signaux permettraient de synchroniser des lectures et des écritures.