Théorie des jeux combinatoires

Temps de lecture15 min

En bref

Résumé de l’article

Dans cet article, nous vous présentons quelques éléments de la “théorie des jeux”. Cette branche des mathématiques étudie les stratégies et a de nombreuses applications dans des domaines tels que l’optimisation, la politique ou l’économie.

À retenir

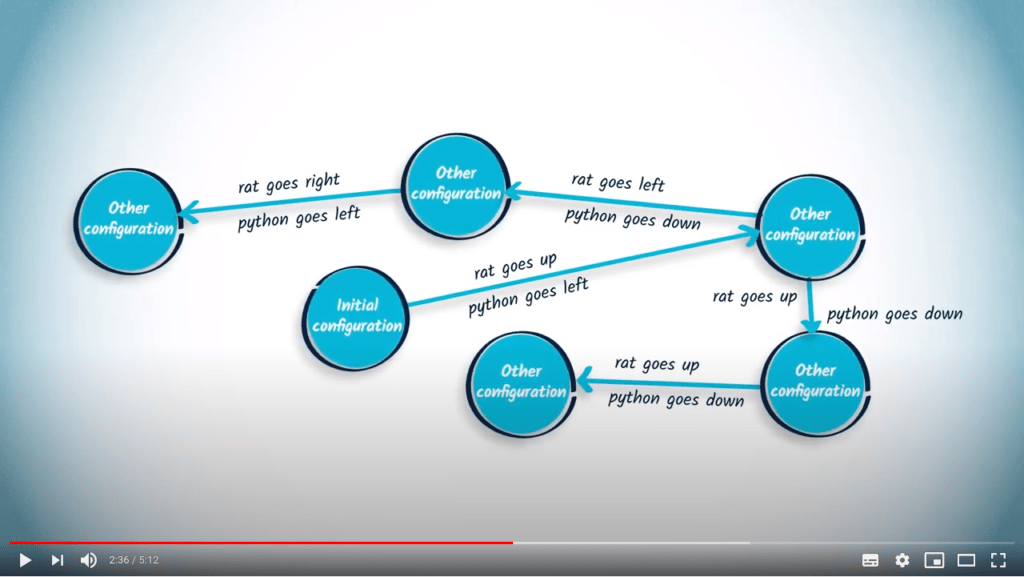
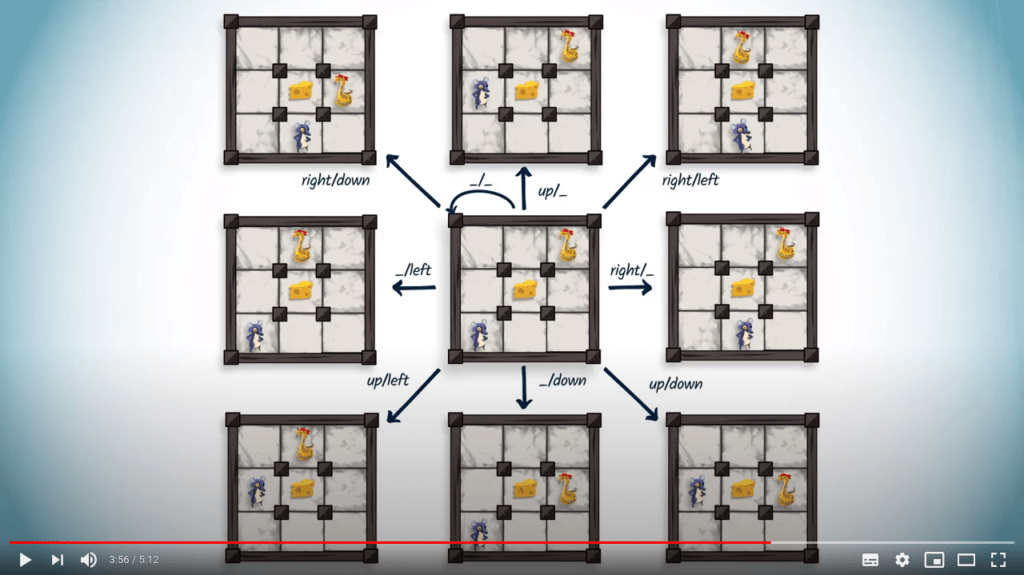
  • La théorie des jeux représente un jeu dans un espace abstrait de configurations.

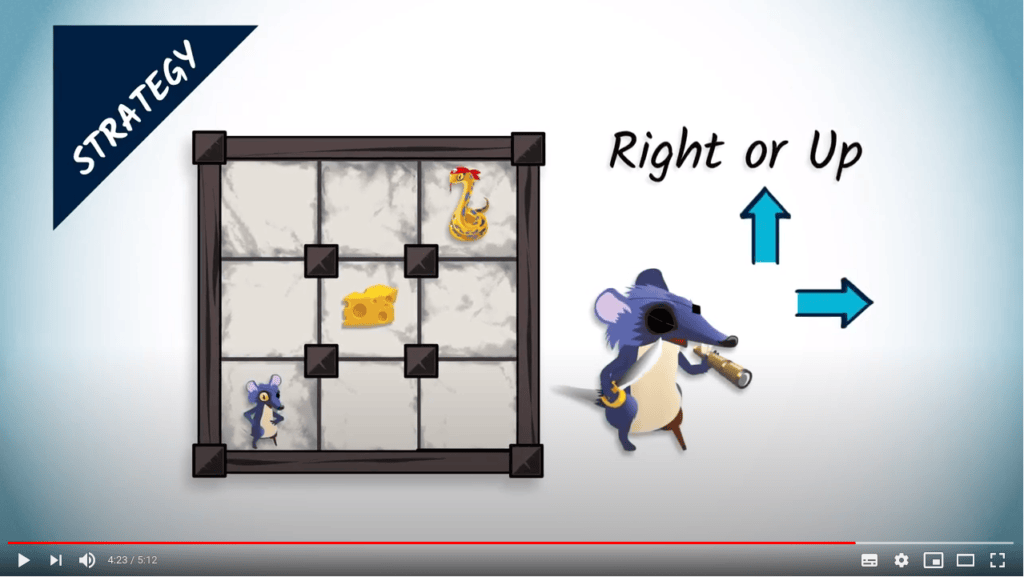
  • Une stratégie consiste en une fonction qui explique quelle prochaine configuration atteindre, étant donnée la configuration actuelle du jeu.

  • Il existe des résultats mathématiques sur les jeux, comme le théorème de von Neumann.

  • Ces résultats s’appliquent à de nombreux domaines de la vie réelle.

Contenu de l’article

1 — Vidéo

Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Information

C’est encore moi ! Bienvenue, je suis si heureux de vous revoir. Commençons par quelques notions de base sur la théorie des jeux.

La théorie des jeux est le domaine de la science qui s’intéresse à l’étude des jeux, des stratégies et des conditions de victoire.

Contexte

Les jeux jouent un rôle important dans de nombreux domaines de la science. Les jeux sont largement utilisés en économie et en mathématiques, mais ont également des applications en cryptographie où, typiquement, l’objectif d’un jeu est de protéger des informations, ainsi que dans les systèmes d’exploitation où l’objectif du jeu est généralement d’éviter les erreurs, ou en intelligence artificielle.

Les jeux constituent un cadre très adapté pour notre jeu dans le labyrinthe, et une excellente excuse pour étudier des algorithmes avancés.

Si vous parvenez à coder un programme qui calcule les positions gagnantes dans un jeu, vous serez prêt pour à peu près n’importe quel défi de programmation !

Définitions de base

Rappelez-vous que nous aimerions jouer à un jeu dans un labyrinthe où deux joueurs, un rat et un python, essaient d’attraper tous les morceaux de fromage avant leur adversaire.

Pendant le jeu, ces joueurs peuvent prendre des décisions simultanées. Par exemple, le python peut décider de se déplacer à gauche pendant que le rat décide de se déplacer vers le haut.

Pour décrire un jeu, nous utilisons un graphe très spécifique que nous appelons l’“arène”. L’arène est un graphe où chaque sommet résume l’état actuel du jeu. Par état du jeu, nous entendons les positions des joueurs, les positions des morceaux de fromage restants et le score de chaque joueur.

Par exemple, il y a un sommet initial qui correspond à la configuration initiale où le rat et le python ont tous deux un score de 0 et sont à leurs positions de départ, et tous les morceaux de fromage sont répartis dans le labyrinthe. Ensuite, il y a également des sommets correspondant à toutes les configurations possibles qui pourraient survenir pendant une partie de PyRat. Les sommets sont reliés par des arêtes qui sont étiquetées selon deux variables. La première variable correspond à la décision prise par le rat et la deuxième variable à la décision prise par le python.

Êtes-vous prêt pour un exemple ? Considérons un jeu simple où un labyrinthe 3 par 3 contient un seul morceau de fromage au centre et le rat et le python sont tous deux en compétition pour l’obtenir. À partir de la configuration initiale, plusieurs choses peuvent se produire. Le rat peut se déplacer à droite, vers le haut, ou rester immobile, et le python peut se déplacer à gauche, vers le bas, ou rester immobile. Nous avons donc 3 fois 3, soit 9, configurations qui peuvent être atteintes à partir de la configuration initiale.

Voici ce qui se passe si le rat se déplace vers le haut et le python se déplace à gauche. Voici ce qui se passe si le rat se déplace vers le haut et le python reste immobile. Voici ce qui se passe si le rat se déplace vers le haut et le python se déplace vers le bas. Voici ce qui se passe si le rat se déplace à droite et le python se déplace à gauche. Voici ce qui se passe si le rat se déplace à droite et le python reste immobile. Voici ce qui se passe si le rat se déplace à droite et le python se déplace vers le bas. Voici ce qui se passe si le rat reste immobile et le python se déplace à gauche. Voici ce qui se passe si le rat reste immobile et le python se déplace vers le bas. Et enfin, voici ce qui se passe si le rat et le python restent tous deux immobiles.

Il existe plusieurs sommets dans l’arène correspondant à la fin du jeu, lorsque le rat ou le python atteint la position centrale qui contient le fromage. Le premier joueur à atteindre cette position sera le gagnant.

Une “stratégie” d’un joueur est une fonction qui associe chaque sommet de l’arène, qui peut également être décrit comme chaque état du jeu, avec un mouvement pour ce joueur.

Un exemple de stratégie est un algorithme glouton qui consiste à aller systématiquement vers le morceau de fromage le plus proche dans le labyrinthe. Une fois que les deux joueurs ont choisi leurs stratégies, le jeu peut être entièrement connu et le gagnant peut être identifié en laissant le jeu de PyRat se dérouler.

Ainsi, une partie peut être vue comme un parcours dans l’arène, en fonction des deux stratégies choisies.

Conclusion

Alors, c’est tout de ma part ! Dans la prochaine leçon, Patrick vous montrera comment calculer de bonnes stratégies.

Pour aller plus loin

2 — Le théorème du minimax de von Neumann

2.1 — Catégories de jeux

Il existe plusieurs catégories de jeux, selon que les joueurs jouent simultanément (e.g., pierre-papier-ciseaux) ou non (e.g., échecs), si les joueurs peuvent cacher certaines informations (e.g., poker), etc.

Dans le cas de PyRat, nous considérons un jeu qui est “simultané”. Cela signifie que les deux joueurs prennent des décisions en même temps. C’est le cas dans une partie normale de PyRat, car les mouvements sont appliqués à une période fixe.

PyRat est également un jeu à “information parfaite”, car toutes les informations sur le plateau, toutes les décisions possibles qui peuvent être prises (et les gains qui en résulteraient), ainsi que l’objectif du jeu, sont connus de tous les joueurs.

De plus, le jeu est “non coopératif”, car chaque joueur essaie de gagner contre l’autre.

En outre, PyRat est un jeu à “somme nulle”, car un morceau de fromage pris par le joueur ne sera pas pris par l’adversaire.

Enfin, PyRat admet un nombre fini de stratégies pures, car le nombre de décisions possibles par sommet de l’arène est un entier. Une stratégie pure est une définition complète de la façon dont un joueur jouera à un jeu. En particulier, elle détermine le mouvement qu’un joueur fera pour toute situation à laquelle il pourrait être confronté. Lorsqu’une stratégie attribue des probabilités à chaque décision, on parle de stratégie mixte.

2.2 — Le théorème

Le théorème du minimax de John von Neumann est un résultat important en théorie des jeux. Dans un jeu non coopératif, simultané avec information parfaite, avec un nombre fini de stratégies pures et à somme nulle, le théorème stipule qu’il existe au moins une situation d’interaction stable, à savoir une situation dans laquelle aucun des deux joueurs n’a intérêt à changer sa stratégie mixte si l’autre ne la change pas.

En d’autres termes, ce que dit le théorème, c’est qu’il existe une situation dans laquelle les deux joueurs devraient se stabiliser, car changer de stratégie n’améliorerait pas les gains tant que l’adversaire ne change pas non plus de stratégie.

Pour aller encore plus loin