Recursive algorithms

Reading time5 min

In brief

Article summary

In this article, we present you what a recursive algorithm is. In particular, we study the case of the factorial function, and show how to write it in a recursive way. We then show what happens in the call stack when executing this function.

Main takeaways

  • Recursive functions are functions that call themselves.

  • They consist of a base case and a recursive call.

  • They are generally simpler and more elegant, but may require a small extra computational cost.

  • Some data structures can also be defined recursively.

Article contents

1 — What is recursion?

Recursion is a fundamental concept in computer programming that occurs when a function calls itself directly or indirectly. A data structure can also be defined recursively.

A recursive function consists of two main elements:

  • The base case – This is the condition that ends the recursion. Without a base case, the function would call itself indefinitely, resulting in a stack overflow error. Note that the base case is not necessarily unique.

  • The recursive call – This is when the function calls itself with a modified set of parameters, bringing the calculus closer to the base case.

2 — A quick example

A classic example of recursion is calculating the factorial of a number. The factorial of $n$ (noted $n!$) is the product of all positive integers less than or equal to $n$:

$$\begin{align*} n! &= \underbrace{1}_{1!} \times 2 \times \dots \times (n-1) \times n\\ n! &= \underbrace{1 \times 2}_{2!} \times \dots \times (n-1) \times n\\ n! &= \underbrace{1 \times 2 \times 3}_{3!} \times \dots \times (n-1) \times n\\ &\dots\\ n! &= \underbrace{1 \times 2 \times 3\times \dots \times (n-1)}_{(n-1)!} \times n\\ n! &= (n-1)! \times n\\ \end{align*}$$

Which can be formalized as:

$$\begin{align*} n! &= \begin{cases} 1 & \text{if $n=1$}.\\ n\times (n-1)! & \text{if $n>0$}. \end{cases} \end{align*}$$

This last formulation puts into perspective the recursive connection between $n!$ and $(n-1)!$ as well as the base case:

  • Base case – When $n=1$, then the function returns $1$. The factorial mathematical formula extends the definition to $0! = 1$.

  • Recursive call – For the rest, we have $n! = n\times (n-1)!$.

In terms of code, this directly translates as follows:

​
def factorial (n: int) -> int:

    """
        This function calculates the factorial of a number n.
        The factorial of a number n is the product of all positive integers less than or equal to n.
        For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
        The factorial of 0 is 1.
        In:
            * n: The number whose factorial is to be calculated.
        Out:
            * The factorial of n.
    """

    # Base case that determines when to stop
    if n == 0:
        return 1
    
    # Recursive call that determines how to continue
    return n * factorial(n - 1)



# Don't forget to test your function
assert factorial(0) == 1
assert factorial(1) == 1
assert factorial(5) == 120
/**
 * To run this code, you need to have Java installed on your computer, then:
 * - Create a file named `Main.java` in a directory of your choice.
 * - Copy this code in the file.
 * - Open a terminal in the directory where the file is located.
 * - Run the command `javac Main.java` to compile the code.
 * - Run the command `java -ea Main` to execute the compiled code.
 * Note: '-ea' is an option to enable assertions in Java.
 */
public class Main {

    /**
     * This function calculates the factorial of a number n.
     * The factorial of a number n is the product of all positive integers less than or equal to n.
     * For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
     * The factorial of 0 is 1.
     *
     * @param n The number whose factorial is to be calculated.
     * @return The factorial of n.
     */
    public static int factorial(int n) {
        // Base case that determines when to stop
        if (n == 0) {
            return 1;
        }

        // Recursive call that determines how to continue
        return n * factorial(n - 1);
    }


    /**
     * This is the entry point of your program.
     * It contains the first codes that are going to be executed.
     *
     * @param args Command line arguments received.
     */
    public static void main(String[] args) {
        // Don't forget to test your function
        assert factorial(0) == 1;
        assert factorial(1) == 1;
        assert factorial(5) == 120;
    }

}
Information

In the case of factorial, the result is guaranteed only for positive numbers. This is the responsability of the developper to ensure the correct usage of their code. For instance, the documentation of this function should mention how it deals with negative numbers.

You could also use assertions to transform your code as follows:

​
def factorial (n: int) -> int:

    """
        This function calculates the factorial of a number n.
        The factorial of a number n is the product of all positive integers less than or equal to n.
        For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
        The factorial of 0 is 1.
        In:
            * n: The number whose factorial is to be calculated.
        Out:
            * The factorial of n.
    """

    # Make sure that n has a correct value
    assert n >= 0

    # Base case that determines when to stop
    if n == 0:
        return 1
    
    # Recursive call that determines how to continue
    return n * factorial(n - 1)



# Don't forget to test your function
assert factorial(0) == 1
assert factorial(1) == 1
assert factorial(5) == 120
/**
 * To run this code, you need to have Java installed on your computer, then:
 * - Create a file named `Main.java` in a directory of your choice.
 * - Copy this code in the file.
 * - Open a terminal in the directory where the file is located.
 * - Run the command `javac Main.java` to compile the code.
 * - Run the command `java -ea Main` to execute the compiled code.
 * Note: '-ea' is an option to enable assertions in Java.
 */
public class Main {

    /**
     * This function calculates the factorial of a number n.
     * The factorial of a number n is the product of all positive integers less than or equal to n.
     * For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
     * The factorial of 0 is 1.
     *
     * @param n The number whose factorial is to be calculated.
     * @return The factorial of n.
     */
    public static int factorial(int n) {
        // Make sure that n has a correct value
        assert n >= 0;

        // Base case that determines when to stop
        if (n == 0) {
            return 1;
        }

        // Recursive call that determines how to continue
        return n * factorial(n - 1);
    }


    /**
     * This is the entry point of your program.
     * It contains the first codes that are going to be executed.
     *
     * @param args Command line arguments received.
     */
    public static void main(String[] args) {
        // Don't forget to test your function
        assert factorial(0) == 1;
        assert factorial(1) == 1;
        assert factorial(5) == 120;
    }
}

3 — Advantages and disadvantages

The main advantages of using recursion are that recursive functions are most of the time clearer, simpler, shorter and easier to understand than their non-recursive counterparts.

Recursion is based upon calling the same function over and over. A recursive function call is often more expensive than a loop (i.e., its non-recursive version). Thus, the overheads associated with a recursive function call are:

  • Space – A function call needs space for parameters and local variables, and an indication of where to return. This space is allocated on the “stack” and released when the function returns. A recursive algorithm may need space proportional to the number of nested calls.

  • Time – Calling a function takes time because it allocates and releases local memory, copies values into it, etc.

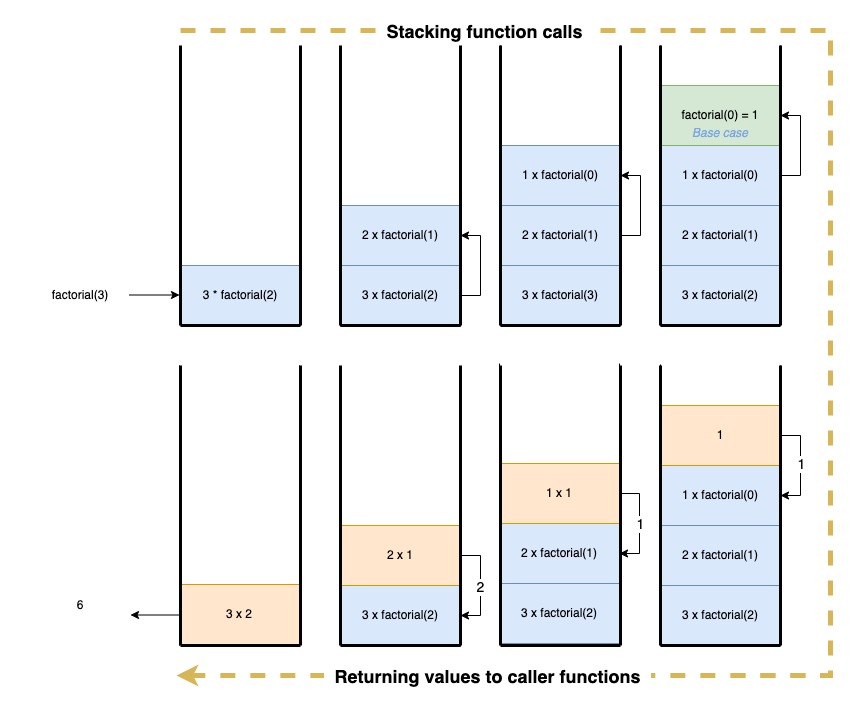
4 — The call stack

Recursion in program execution involves several key steps, including managing function calls, creating new function instances and managing the call stack.

Here’s an illustration of how the stack is used when calling factorial(3):

To go further

Important

The content of this section is optional. It contains additional material for you to consolidate your understanding of the current topic.

5 — Tail recursion

In traditional recursion (example above), you first make the recursive calls and then use their intermediary results to calculate the final result.

This process can be modified to:

  • First – calculate the intermediary result.

  • Then – Pass it as an argument to the recursive call. The recursive call is returned as is, i.e., without a posteriori operations.

This way of doing is called tail recursion. Some smart compilers can recognize this form of recursion and turn it into loops (executed in “constant space”).

Information

Remember that the aim of this lesson is to understand recursion so that you can develop simple and correct recursive methods, regardless of their efficiency.

For the record, here is the way to code the factorial function in a tail recursion:

​
def factorial_tail (n: int, tmp_result: int = 1) -> int:

    """
        This function calculates the factorial of a number n.
        The factorial of a number n is the product of all positive integers less than or equal to n.
        For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
        The factorial of 0 is 1.
        In:
            * n:          The number whose factorial is to be calculated.
            * tmp_result: The current result of the factorial calculation.
        Out:
            * The factorial of n.
    """

    # Base case that determines when to stop
    if n == 0:
        return tmp_result

    # Recursive call that determines how to continue
    return factorial_tail(n - 1, n * tmp_result)



# Don't forget to test your function
assert factorial_tail(0) == 1
assert factorial_tail(1) == 1
assert factorial_tail(5) == 120
/**
 * To run this code, you need to have Java installed on your computer, then:
 * - Create a file named `Main.java` in a directory of your choice.
 * - Copy this code in the file.
 * - Open a terminal in the directory where the file is located.
 * - Run the command `javac Main.java` to compile the code.
 * - Run the command `java -ea Main` to execute the compiled code.
 * Note: '-ea' is an option to enable assertions in Java.
 */
public class Main {

    /**
     * This function calculates the factorial of a number n.
     * The factorial of a number n is the product of all positive integers less than or equal to n.
     * For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
     * The factorial of 0 is 1.
     *
     * @param n         The number whose factorial is to be calculated.
     * @param tmpResult The current result of the factorial calculation.
     * @return The factorial of n.
     */
    public static int factorialTail(int n, int tmpResult) {
        // Base case that determines when to stop
        if (n == 0) {

            return tmpResult;
        }

        // Recursive call that determines how to continue
        return factorialTail(n - 1, n * tmpResult);
    }


    /**
     * This is the entry point of your program.
     * It contains the first codes that are going to be executed.
     *
     * @param args Command line arguments received.
     */
    public static void main(String[] args) {
        // Don't forget to test your function
        assert factorialTail(0, 1) == 1;
        assert factorialTail(1, 1) == 1;
        assert factorialTail(5, 1) == 120;
    }

}

The method expects two arguments: n and the initial value of tmp_result. Given the accumulation operation (*), the second parameter must be set to 1 in the initial call.

Here’s an illustration of how the stack is used when calling factorial_tail(3, 1):

Information

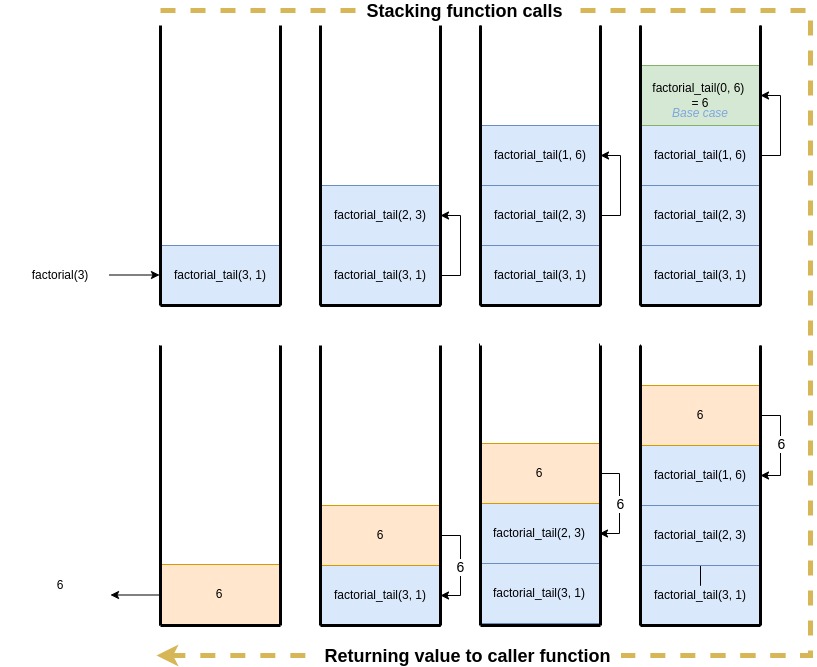
It should be noted that no calculus is applied to the return value. The final result, 6, is not modified once it has been computed.

6 — Recursive data structures

Although we will not go into it details here, recursion can also occur in data structures.

A common example is the linked list. A linked list is a data structure where elements are stored in separate locations and linked together using references. Each node has two parts:

  • Data – The element to store in the node.
  • Link –A reference to the next node.

In a linked list, the last node typically has a reference that is set to None (or null in Java), indicating that there are no further nodes in the sequence. This structure is efficient for inserting and deleting elements because it doesn’t require adapting the size or shifting elements, like in an array.

A binary tree can also be represented by nodes made up of four parts:

  • Data – The element to store in the node.
  • Parent link – A reference to the parent node.
  • Left child link – A reference to the left child node.
  • Right child link – A reference to the right child node.

The parent of the root node is null, as are the child nodes of leaves. The path of a tree represented in this way is simple to express using a recursive function.

To go beyond

Important

The content of this section is very optional. We suggest you directions to explore if you wish to go deeper in the current topic.