Algorithmes récursifs
Reading time5 minEn bref
Résumé de l’article
Dans cet article, nous vous présentons ce qu’est un algorithme récursif. En particulier, nous étudions le cas de la fonction factorielle, et montrons comment l’écrire de manière récursive. Nous montrons ensuite ce qui se passe dans la pile d’appels lors de l’exécution de cette fonction.
Points clés
-
Les fonctions récursives sont des fonctions qui s’appellent elles-mêmes.
-
Elles consistent en un cas de base et un appel récursif.
-
Elles sont généralement plus concises et plus élégantes, mais peuvent nécessiter un coût de calcul supplémentaire.
Contenu de l’article
1 — Qu’est-ce que la récursivité ?
La récursivité est un concept fondamental en programmation informatique qui se produit lorsqu’une fonction s’appelle elle-même directement ou indirectement. Une structure de données peut également être définie récursivement.
Une fonction récursive se compose de deux éléments principaux :
-
Le cas de base – C’est la condition qui met fin à la recursion. Sans cas de base, la fonction s’appellerait indéfiniment, ce qui entraînerait une erreur de dépassement de pile (stack overflow). Notez que le cas de base n’est pas nécessairement unique.
-
L’appel récursif – C’est lorsque la fonction s’appelle elle-même avec un ensemble modifié de paramètres, rapprochant le calcul du cas de base.
2 — Un exemple rapide
Un exemple classique de récursion est le calcul de la factorielle d’un nombre. La factorielle de $n$ (notée $n!$) est le produit de tous les entiers positifs inférieurs ou égaux à $n$ :
$$\begin{align*} n! &= \underbrace{1}_{1!} \times 2 \times \dots \times (n-1) \times n\\ n! &= \underbrace{1 \times 2}_{2!} \times \dots \times (n-1) \times n\\ n! &= \underbrace{1 \times 2 \times 3}_{3!} \times \dots \times (n-1) \times n\\ &\dots\\ n! &= \underbrace{1 \times 2 \times 3\times \dots \times (n-1)}_{(n-1)!} \times n\\ n! &= (n-1)! \times n\\ \end{align*}$$Ce qui peut se formaliser ainsi :
$$\begin{align*} n! &= \begin{cases} 1 & \text{si $n=1$}.\\ n\times (n-1)! & \text{si $n>0$}. \end{cases} \end{align*}$$Cette dernière formulation met en perspective la relation récursive entre $n!$ et $(n-1)!$ ainsi que le cas de base :
-
Cas de base – Lorsque $n=1$, la fonction retourne $1$. La formule mathématique de la factorielle étend la définition à $0! = 1$.
-
Appel récursif – Pour le reste, on a $n! = n\times (n-1)!$.
En termes de code, cela se traduit directement comme suit :
def factorial (n: int) -> int:
"""
This function calculates the factorial of a number n.
The factorial of a number n is the product of all positive integers less than or equal to n.
For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
The factorial of 0 is 1.
In:
* n: The number whose factorial is to be calculated.
Out:
* The factorial of n.
"""
# Base case that determines when to stop
if n == 0:
return 1
# Recursive call that determines how to continue
return n * factorial(n - 1)
# Don't forget to test your function
assert factorial(0) == 1
assert factorial(1) == 1
assert factorial(5) == 120Dans le cas de la factorielle, le résultat est garanti uniquement pour les nombres positifs. C’est la responsabilité du développeur de s’assurer de la bonne utilisation de son code. Par exemple, la documentation de cette fonction devrait mentionner comment elle gère les nombres négatifs.
Vous pouvez également utiliser la programmation défensive ou des assertions pour transformer votre code comme suit :
def factorial (n: int) -> int:
"""
This function calculates the factorial of a number n.
The factorial of a number n is the product of all positive integers less than or equal to n.
For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
The factorial of 0 is 1.
In:
* n: The number whose factorial is to be calculated.
Out:
* The factorial of n.
"""
# Make sure that n has a correct value
assert n >= 0
# Base case that determines when to stop
if n == 0:
return 1
# Recursive call that determines how to continue
return n * factorial(n - 1)
# Don't forget to test your function
assert factorial(0) == 1
assert factorial(1) == 1
assert factorial(5) == 1203 — Avantages et inconvénients
Les principaux avantages de l’utilisation de la récursivité sont que les fonctions récursives sont la plupart du temps plus claires, plus simples, plus courtes et plus faciles à comprendre que leurs équivalents non récursifs.
La récursivité repose sur l’appel répété de la même fonction. Un appel de fonction récursive est souvent plus coûteux qu’une boucle (c’est-à-dire sa version non récursive). Ainsi, les surcoûts associés à un appel de fonction récursive sont :
-
Espace – Un appel de fonction nécessite de l’espace pour les paramètres et les variables locales, ainsi qu’une indication de l’endroit où retourner. Cet espace est alloué sur la “pile” et libéré lorsque la fonction retourne. Un algorithme récursif peut nécessiter un espace proportionnel au nombre d’appels imbriqués.
-
Temps – Appeler une fonction prend du temps car cela alloue et libère de la mémoire locale, copie des valeurs dedans, etc.
4 — La pile d’appels
La récursivité dans l’exécution d’un programme implique plusieurs étapes clés, notamment la gestion des appels de fonctions, la création de nouvelles instances de fonctions et la gestion de la pile d’appels.
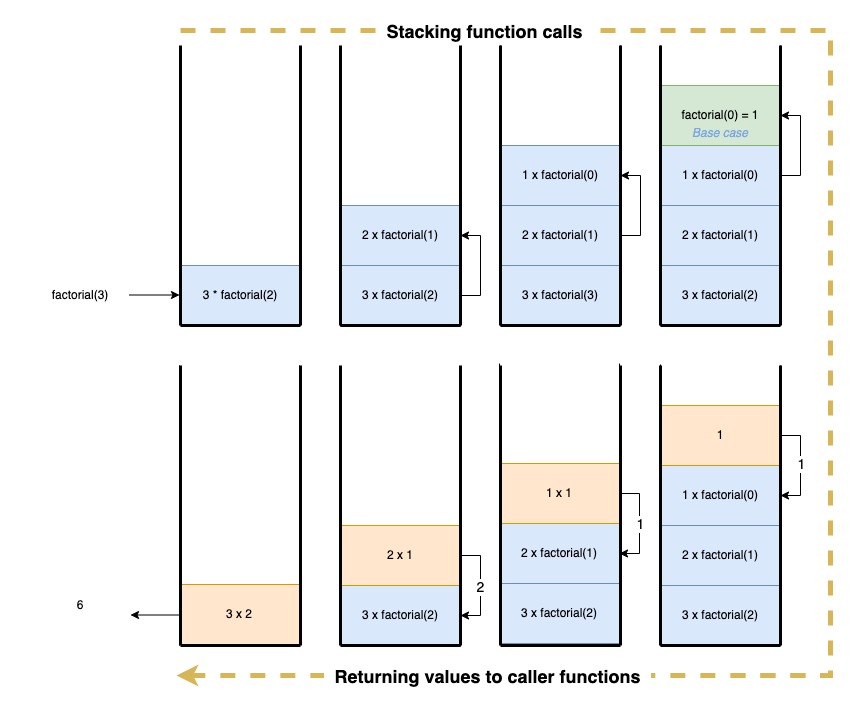
Voici une illustration de l’utilisation de la pile lors de l’appel factorial(3) :
 |
|---|
| Exemple de pile d’appels pour la récursion. |
5 — Récursion terminale
Dans la récursion traditionnelle (exemple ci-dessus), vous effectuez d’abord les appels récursifs puis utilisez leurs résultats intermédiaires pour calculer le résultat final. Cela permet de construire le résultat final en utilisant les résultats des appels récursifs précédents. Le résultat final est alors obtenu au cas d’arrêt.
Ce processus peut être modifié pour :
-
D’abord – calculer le résultat intermédiaire.
-
Puis – le passer en argument à l’appel récursif. L’appel récursif est retourné tel quel, c’est-à-dire sans opérations a posteriori.
Cette façon de faire s’appelle la récursion terminale.
Certains compilateurs intelligents peuvent reconnaître cette forme de récursion et la transformer en boucles (exécutées en “espace constant”).
Rappelez-vous que le but de cette leçon est de comprendre la récursivité afin que vous puissiez développer des méthodes récursives simples et correctes, indépendamment de leur efficacité.
Pour mémoire, voici la manière de coder la fonction factorielle en récursion terminale :
def factorial_tail (n: int, tmp_result: int = 1) -> int:
"""
This function calculates the factorial of a number n.
The factorial of a number n is the product of all positive integers less than or equal to n.
For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.
The factorial of 0 is 1.
In:
* n: The number whose factorial is to be calculated.
* tmp_result: The current result of the factorial calculation.
Out:
* The factorial of n.
"""
# Make sure that n has a correct value
assert n >= 0
# Base case that determines when to stop
if n == 0:
return tmp_result
# Recursive call that determines how to continue
return factorial_tail(n - 1, n * tmp_result)
# Don't forget to test your function
assert factorial_tail(0) == 1
assert factorial_tail(1) == 1
assert factorial_tail(5) == 120La méthode attend deux arguments : n et la valeur initiale de tmp_result.
Étant donné l’opération d’accumulation (*), le second paramètre doit être fixé à 1 lors de l’appel initial.
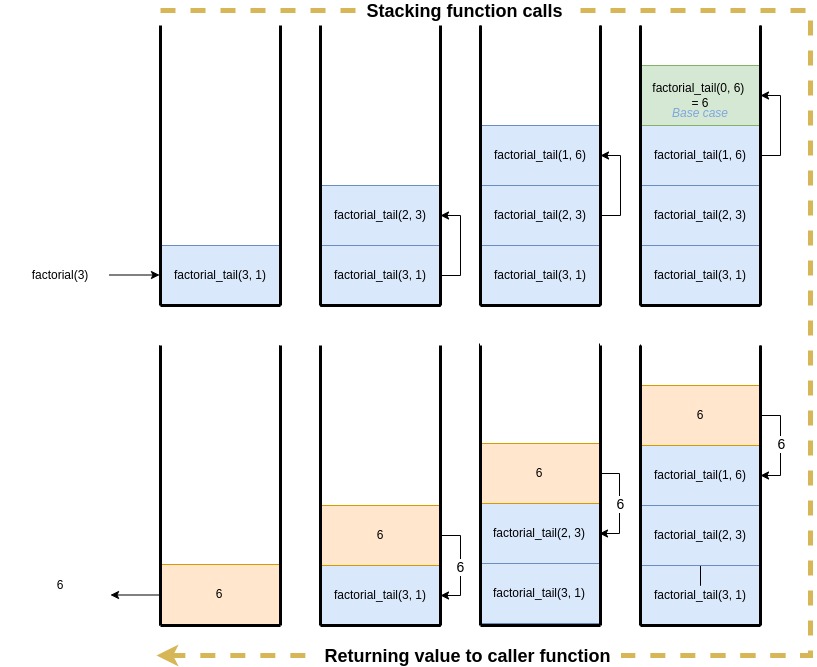
Voici une illustration de l’utilisation de la pile lors de l’appel factorial_tail(3, 1) :
 |
|---|
| Exemple de pile d’appels pour la récursion terminale. |
Il faut noter qu’aucun calcul n’est appliqué à la valeur de retour.
Le résultat final, 6, n’est pas modifié une fois qu’il a été calculé.
6 — Correction et terminaison
Un algorithme récursif doit être correct et terminer.
- Correction – Un algorithme récursif est correct s’il produit le résultat attendu pour toutes les entrées valides. Pour la fonction factorielle, cela signifie qu’elle doit retourner la valeur correcte pour tous les entiers non négatifs.
- Terminaison – Un algorithme récursif doit terminer pour toutes les entrées valides. Pour la fonction factorielle, cela signifie qu’elle doit atteindre le cas de base pour tous les entiers non négatifs. Si l’algorithme ne termine pas, il peut entraîner une erreur de dépassement de pile (stack overflow) en raison d’appels récursifs infinis.
Preuve de terminaison
Pour prouver qu’un algorithme récursif termine, la méthode la plus courante est de se baser sur une relation d’ordre sur les entrées. Dans le cas de la fonction factorielle, nous pouvons utiliser l’ordre naturel des entiers non négatifs. Nous pouvons prouver que la fonction termine en montrant que :
- Pour chaque appel récursif, l’argument
ndiminue de1. - Lorsque
natteint0, le cas de base est atteint et la fonction retourne1.
Ainsi, la fonction ne s’appelle jamais avec un argument négatif, et elle termine pour tous les entiers non négatifs.
Preuve de correction
Pour prouver qu’un algorithme récursif est correct, nous devons montrer que :
- Le cas de base retourne la valeur correcte.
- L’appel récursif produit le résultat correct en utilisant la relation de récurrence.
Dans le cas de la fonction factorielle, nous pouvons prouver que :
- Le cas de base retourne
1pour0, ce qui est correct. - L’appel récursif retourne
n * (n-1)!, ce qui est correct par définition de la factorielle.
Ainsi, la fonction retourne la valeur correcte pour tous les entiers non négatifs.