Complexité algorithmique

Reading time20 min

En bref

Résumé de l’article

La complexité algorithmique est une notion fondamentale en informatique. Elle permet de caractériser un algorithme et de fournir une estimation du temps et de l’espace nécessaire à son exécution, en fonction de ses entrées. Cela permet d’évaluer si un problème peut être résolu dans un temps et un espace mémoire raisonnable, mais aussi de comparer plusieurs algorithmes qui résolvent un même problème. De plus, c’est une mesure qui ne dépend pas de la qualité de votre processeur, car elle ne nécessite pas l’exécution du programme.

Points clés

La complexité algorithmique estime le temps et l’espace nécessaire à l’exécution d’un algorithme.
La complexité s’exprime en fonction de la taille de l’entrée.
Il existe des classes de complexité.
On s’intéresse généralement à la complexité dans le pire des cas, mais d’autres mesures existent.
Dans la pratique, le temps et l’espace sont souvent échangeables. Cherchant à soit accélérer un programme en consommant plus de mémoire ou inversement.

Contenu de l’article

Complexité algorithmique

Le but de tout algorithme est de proposer une solution à un problème donné. La qualité d’un algorithme s’évalue principalement selon deux critères : le temps d’exécution et l’espace mémoire utilisé. Il existe des cas d’application où seul compte le fait d’avoir le résultat le plus vite possible et d’autres où bien que l’on veuille aller le plus vite possible, la contrainte majeure vient de l’espace mémoire restreint.

1 — Complexité temporelle

Minimiser le temps de traitement d’un algorithme est directement lié au nombre de calculs effectués.

La complexité algorithmique est une mesure de la performance d’un programme en termes de nombre de calculs qu’il réalise. Pour évaluer le temps d’exécution d’un calcul, il faut évaluer et cumuler le temps que requiert chaque instruction participant au calcul. Les différent facteurs qui influences le temps d’exécution sont :

Les données du problème.
L’algorithme utilisé pour résoudre le problème.

Mais il faut également prendre en compte :

Le matériel (hardware) comme la vitesse du processeur, la vitesse d’accès à la mémoire, sa taille, le temps de transfert de données vers les disques, etc…
Le logiciel utilisé (software) comme le langage de programmation, les interpréteurs et compilateurs, IDE etc…
La charge de la machine comme par exemple le nombre de processus qui s’exécutent.
etc

On se rend bien compte que calculer de manière rigoureuse le temps d’exécution d’un algorithme devient extrêmement compliqué. C’est pour cela qu’en informatique, nous simplifions l’analyse en approximant le temps d’exécution avec un modèle simplifié autour des principales opérations élémentaires coutant une unité de temps.

Les opérations élémentaires les plus importantes sont :

$T_{AM}$ : Temps de l’accès mémoire.
$T_{ADD}$, $T_{SUB}$, $T_{MUL}$, $T_{DIV}$ : Temps d’une addition, soustraction, multiplication ou division.
$T_{CMP}$ : Temps d’une comparaison simple.
$T_{ES}$ : Temps d’une entrée/sortie en lecture/écriture.

Pour chaque algorithme, le temps de calcul est décrit par un polynôme prenant compte des données et des opérations élémentaires. Notons $f$ cette fonction.

Regardons sur cet exemple comment évaluer le coût de la méthode func(a,b).

  def func(a: int, b: int):
    x = a   
    y = b
    while x !=y
      if x > y :
        x = x-y
      else :
        y = y-x
    return x

Analysons chaque instruction simple :

Initialiser les variables x et y demande deux transferts vers la mémoire $\rightarrow 2*T_{AM}$
Comparer x et y dans la condition de la boucle while $\rightarrow T_{CMP}$
Comparer x et y dans la condition du if $\rightarrow T_{CMP}$
La soustraction dans la clause Alors ou Sinon n’est faite qu’une fois $\rightarrow T_{SUB}$
Suite à la soustraction, le résultat est mis en mémoire dans x ou y $\rightarrow T_{AM}$
L’opération return demande un transfert vers la mémoire $\rightarrow T_{AM}$

En supposant que le nombre d’itérations de la boucle while est n, le temps de calcul est :

$$f(n) = 2*T_{AM} + n *(T_{CMP} + T_{CMP} + T_{SUB} + T_{AM}) + T_{AM} $$ $$ = 3*T_{AM} + n*(2*T_{CMP}+ T_{SUB} + T_{AM}) $$

Nous observons que bien que la taille et valeur des données vont jouer sur ce coût, il est aussi dépendant des temps machines pour l’accès en mémoire, et opérations en tout genre. Ainsi, calculer de façon précise le temps de calcul d’un algorithme est généralement impossible. C’est pour cela que, quelle que soit la machine utilisée, nous considérons que toutes les opérations élémentaires sont effectuées en temps constant (égal à 1), donc : $f(n) = 3 + 6\times n$. Le calcul de la complexité revient donc à analyser le nombre d’opérations élémentaires effectuées par l’algorithme.

Les boucles sont la principale cause du grand nombre de calculs. Une utilisation non contrôlée conduit à un nombre croissant d’opérations. Au-delà d’un certain nombre, le temps de calcul devient un obstacle à l’utilisation du programme. Il est donc important de pouvoir évaluer la performance d’un algorithme avant de le programmer.

2 — Analyse de la complexité

Il existe plusieurs méthodes d’analyse de la complexité, notamment :

L’analyse moyenne fournit des informations sur le temps moyen de calcul.
L’analyse pessimiste (pire cas) est la plus couramment utilisée. Elle fournit des informations sur le nombre de calculs à considérer dans un scénario de pire cas.

Son objectif principal est d’évaluer les algorithmes dans leurs cas les plus extrêmes. Par exemple, si un algorithme cherche un élément parmi $n$ données initiales, dans le pire des cas il devra parcourir toutes les données.

Pour cela nous nous intéressons à la variation du coût en fonction de la taille des données, plus exactement l’asymptote vers laquelle tend ce coût lorsque la taille du problème tend vers l’infini.

Les notations asymptotiques (ou notations de Landau) permettent de décrire le comportement d’un algorithme et de sa croissance sans se soucier des constantes ni des termes de faible importance. Il y a trois grandes notations asymptotiques :

La borne asymptotique supérieure définie par $O(.)$
La borne asymptotique inférieure définie par $\Omega(.)$
La borne asymptotique définie par $\Theta(.)$

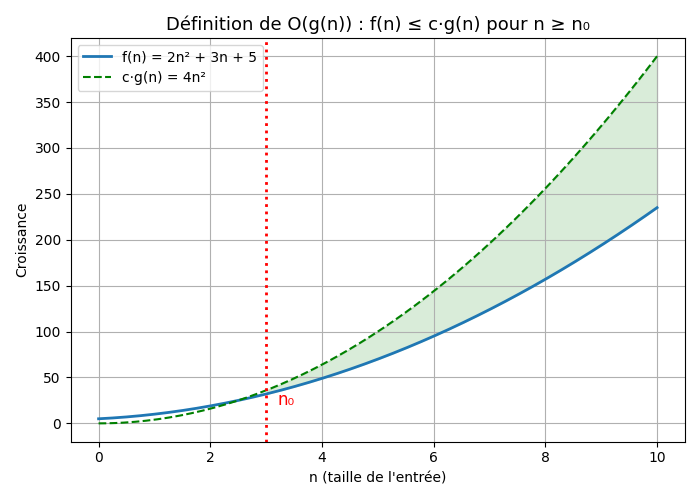
La borne asymptotique supérieure

Soit $f(n)$ la fonction décrivant la complexité de notre algorithme, $f(n) \in O(g(n))$ si elle ne croît pas plus vite que $g(n)$. Sa définition mathématique est :

$$O(g(n)) = \{ f : \mathbb{N} \rightarrow \mathbb{N} \vert \exists c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}\ tels\ que\ \forall n \geq n_0 : 0 \leq f(n) \leq c.g(n)\}$$

Notons que par abuse de langage, on écrit souvent $f(n) = O(g(n))$.

Borne asymptotique supérieure

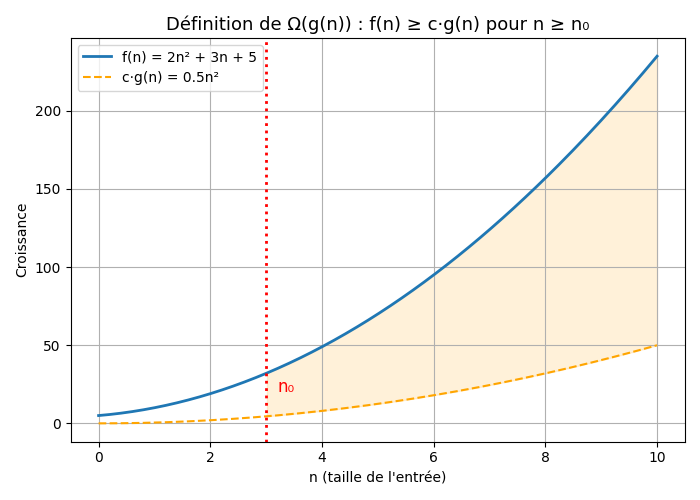
La borne asymptotique inférieure

$f(n) \in \Omega(g(n))$ si elle ne croît pas moins vite que $g(n)$. Sa définition mathématique est :

$$\Omega(g(n)) = \{ f : \mathbb{N} \rightarrow \mathbb{N} \vert \exists c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}\ tels\ que\ \forall n \geq n_0 : 0 \leq c.g(n) \leq f(n) \}$$

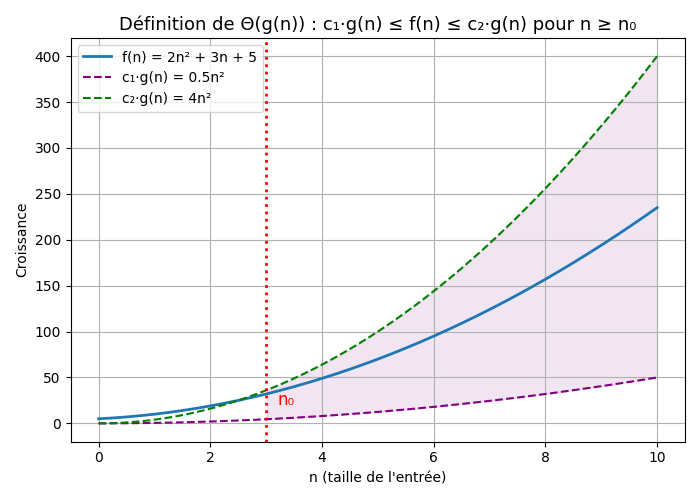
Borne asymptotique supérieure

La borne asymptotique

$f(n) \in \Theta(g(n))$ si elle ne croît pas plus vite que $g(n)$. Sa définition mathématique est :

$$\Theta(g(n)) = \{ f : \mathbb{N} \rightarrow \mathbb{N} \vert \exists c_1 \in \mathbb{R}^+, c_2 \in \mathbb{R}^+ \exists n_0 \in \mathbb{N}\ tels\ que\ \forall n \geq n_0 : c_1.g(n) \leq f(n) \leq c_2.g(n)\}$$

Borne asymptotique

Exemple de bornes asymptotiques

$$f(n) = n^3 + 2n^2 +4n +2 \in O(n^3)\ \text{puisque, pour } n\geq 1 \text{, on a } f(n) \leq 10 n^3.$$ $$f(n) = n .log(n) +12n + 478 \in O(n .log(n)) $$ $$f(n) = n + \sqrt{n} \in \Omega(n .log(n)) $$ $$f(n) =\sum_{i=0}^p a_i*n^i \in \Theta(n^p) $$

Le comportement du coût d’un algorithme quand les données en entrée augmentent peut donc être analysé grâce à des fonctions mathématiques bien connues. Nous pouvons donc classer les algorithmes par complexité croissante quand on considère que $n \rightarrow \infty$. Voici ce que cela donne pour les bornes asymptotiques supérieures :

$$O(1)\leq O(log(n))\leq O(n)\leq O(n.log(n))\leq O(n^2)\leq O(n^k)\leq O(n^{log(n)})\leq O(p^n)\leq O(n!) $$

3 — Reconnaître les catégories de complexité

La plupart des algorithmes sont basés sur des structures de programmation qui peuvent être regroupées dans les catégories de complexité que nous venons donner de manière croissante :

3.1 — Algorithmes constants

Ils sont notés $O(1)$. Ces algorithmes restent constant sans dépendre des données en entrée. C’est par exemple un algorithme réalisant un séquencement d’opérations élémentaires. Ou ajouter/accéder à un élément précis d’une liste. Comme nous l’avions déjà mentionné plus haut, il a été établi que les opérations élémentaires coutaient une unité de temps. Les processeurs actuelles peuvent réaliser environ une dizaine de milliards d’opérations par seconde. Donc une opération élémentaire se fait en un dixième de nanoseconde.

3.1 — Algorithmes logarithmiques

Ils sont notés $O(log(n))$. Ces algorithmes sont très efficaces en termes de temps de traitement. Le nombre de calculs dépend du logarithme du nombre initial de données à traiter. La fonction $log(n)$ a une courbe qui s’aplatit horizontalement à mesure que le nombre de données augmente. Le nombre de calculs augmente légèrement avec la quantité de données à traiter (voir figure ci-dessous).

Information

La fonction logarithme donne un résultat différent selon la base sur laquelle elle est calculée, ex. $log_{10}(1000) = 3$, $log_2(1000)= 9.97$ ou $ln(1000)=6.9$.

Les algorithmes logarithmiques traitent l’ensemble de données en le divisant en deux parties égales, puis répètent le processus sur chaque moitié. C’est le logarithme en base 2, $log_2(n)$. Pour simplifier l’écriture de la complexité de ces algorithmes, la notation $log(n)$ est utilisée au lieu de $log_2(n)$.

Exemple

La recherche dichotomique est l’un de ces algorithmes. Vous cherchez dans la moitié où se trouve la donnée, puis répétez la recherche en divisant la moitié sélectionnée par deux. Cependant, les données doivent être triées au préalable, ce qui fait $log_2(n)$ comparaisons.

3.2 — Algorithmes linéaires

Ils sont notés sous la forme $O(n)$. Ce sont des algorithmes rapides. Le nombre de calculs dépend linéairement du nombre de données initiales à traiter. C’est le cas pour parcourir une liste de $n$ éléments ou faire une boucle sur $n$ itérations.

Exemple

Considérons un algorithme qui cherche un nom dans une liste de 1 000 noms et compare ce nom avec chacun des noms de la liste. Si le traitement de $n=1 000$ données initiales nécessite 3 000 calculs de base pour trouver le résultat, la complexité de l’algorithme est $O(n)$.

3.3 — Algorithmes linéaires et logarithmiques

Ils sont notés sous la forme $O(n \cdot log(n))$. Ce sont des algorithmes qui divisent à plusieurs reprises un ensemble en deux parties et itèrent complètement sur chaque partie. C’est également les complexités des algorithmes de tris par échanges.

Exemple

Considérons un algorithme qui cherche la plus longue sous-séquence croissante. Le but est de trouver une sous-séquence d’une séquence donnée dans laquelle les éléments de la sous-séquence sont triés par ordre croissant et dans laquelle la sous-séquence est la plus longue possible. Cette sous-séquence n’est pas nécessairement contiguë ni unique.

3.4 — Algorithmes polynomiaux

Ils sont notés sous la forme $O(n^p)$, où $p$ est une constante. Les algorithmes dont la complexité est $O(n^2)$ sont aussi appelés quadratiques. C’est le cas lors de deux boucles imbriquées ou lors du parcours d’une matrice $n*n$.

Exemple

Un algorithme qui compare une liste de 1 000 noms avec une autre liste de 1 000 noms, et itère sur la seconde liste pour chaque nom de la première, effectue $1,000 \times 1,000$ calculs. Il est de type $O(n^2)$.

3.5 — Algorithmes exponentiels ou factoriels

Ils sont notés sous la forme $O(e^n)$ ou $O(n!)$. Ce sont parmi les algorithmes les plus complexes. Le nombre de calculs augmente de façon exponentielle ou factorielle selon les données traitées.

Exemple

Un algorithme exponentiel traitant 10 données initiales effectuera 22 026 calculs, tandis qu’un algorithme factoriel en effectuera 3 628 800. Ce type d’algorithme se rencontre couramment dans les problèmes d’intelligence artificielle (IA).

4 — Résumé

Visuellement, on peut comprendre les relations entre les complexités comme suit :

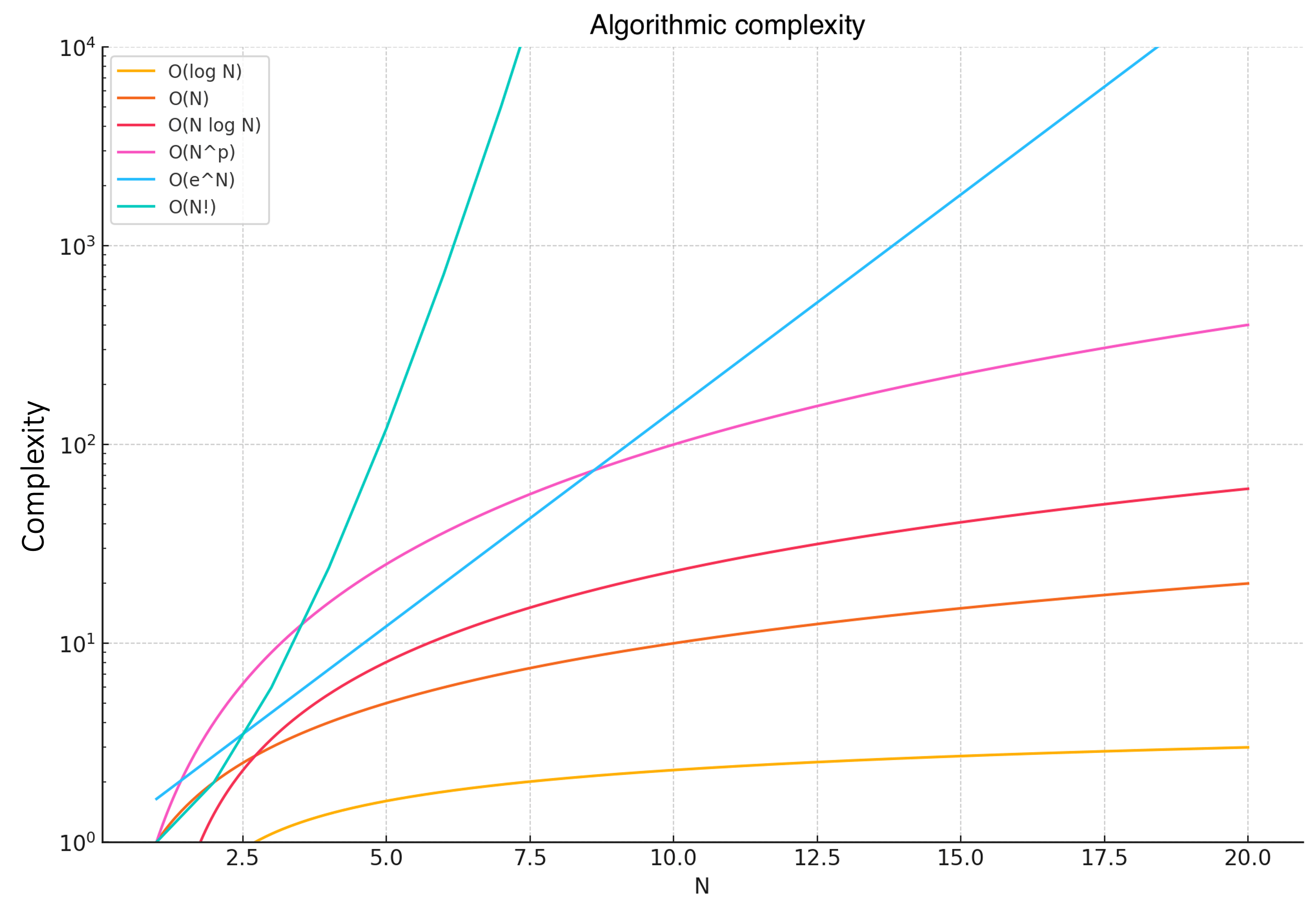
Algorithmic complexity

Les courbes montrent clairement comment chaque fonction de complexité croît avec l’augmentation de $n$.

$O(log(n))$ – Croissance très lente de la courbe (complexité faible).
$O(n)$ – Croissance linéaire de la courbe.
$O(n \cdot log(n))$ – Croissance légèrement plus rapide de la courbe.
$O(n^2)$ – Croissance quadratique.
$O(e^n)$ – Croissance exponentielle (complexité très élevée).
$O(n!)$ – Croissance factorielle (complexité extrêmement élevée).

En supposant qu’une machine actuelle ferait 10 milliards d’opérations élémentaire par seconde, voici une conjecture sur les temps que prendrait des algorithmes avec différentes complexités :

$n$ \ $O(n)$	$n$	$n^2$	$n^3$	$2^n$	$2^{n^2}$
$n=10$	1 ns	10 ns	100 ns	102 ns	4000 milliards d’années
$n=50$	5 ns	250ns	12,5 $\mu$s	1 jour 7h	$\infty$
$n=100$	10 ns	1 $\mu$s	0,1 ms	4000 milliards d’années	$\infty$
$n=10^4$	1 $\mu$s	10 ms	1 min 40s	$\infty$	$\infty$
$n=10^6$	0,1 ms	1 min 40s	3 ans 2 mois	$\infty$	$\infty$
$n=10^9$	0,1 s	2 ans 2 mois	3 milliards d’années	$\infty$	$\infty$

Bien que la gestion de la mémoire ne soit pas incluse dans la notion de complexité, elle en dépend souvent. Il est courant d’utiliser plus de mémoire pour minimiser le nombre d’opérations. Il faut donc vérifier que la gestion mémoire des algorithmes performants ne devienne pas une nouvelle contrainte à leur utilisation.