Complexité spatiale
Reading time15 minEn bref
Résumé de l’article
La complexité algorithmique est une notion fondamentale en informatique. Elle permet de caractériser un algorithme et de fournir une estimation du temps et de l’espace nécessaires à son exécution, en fonction de ses entrées. Cela permet d’évaluer si un problème peut être résolu dans un temps et un espace mémoire raisonnables, mais aussi de comparer plusieurs algorithmes qui résolvent un même problème. De plus, c’est une mesure qui ne dépend pas de la qualité de votre processeur, car elle ne nécessite pas l’exécution du programme.
Points clés
-
La complexité algorithmique estime le temps et l’espace nécessaires à l’exécution d’un algorithme.
-
La complexité s’exprime en fonction de la taille de l’entrée.
-
Il existe des classes de complexité.
-
On s’intéresse généralement à la complexité dans le pire des cas, mais d’autres mesures existent.
-
Dans la pratique, le temps et l’espace sont souvent des notions duales (en ce qui concerne la complexité). On peut chercher à accélérer un programme en consommant plus de mémoire ou inversement.
Contenu de l’article
Complexité algorithmique
Le but premier d’un algorithme est de proposer une solution correcte à un problème donné. Une fois cette condition remplie, il est possible d’évaluer et, éventuellement, d’améliorer celui-ci. L’évaluation d’un algorithme s’effectue principalement selon deux critères : le temps d’exécution et l’espace mémoire utilisé. Il existe des cas d’application où seul compte le fait d’avoir le résultat le plus vite possible et d’autres où bien que l’on veuille aller le plus vite possible, la contrainte majeure vient de l’espace mémoire restreint.
1 — Complexité spatiale
Jusqu’à présent nous avons analysé le comportement temporel des algorithmes que nous avions. Comme expliqué au début de ce cours, chaque opération élémentaire de type $T_{AM}$ peut être simplifié en coût unitaire. Mais dans certain cas, les éléments mis en mémoire demandent des structures auxiliaires qu’il faut stocker et qui peuvent ralentir l’exécution de l’algorithme dû à trop de temps de gestion mémoire.
La complexité spatiale d’un algorithme correspond à l’espace mémoire qu’il nécessite pour être exécuté, elle est définie par celle des données en entrée plus celle auxiliaire générée durant l’algorithme.
Complexité Spatiale totale = Complexité Spatiale en entrée + Complexité Spatiale auxiliaire
Une consommation excessive de mémoire peut engendrer des pertes de performances, voire des échecs d’exécution, notamment avec des ressources limitées. Ainsi, comprendre le comportement mémoire d’un algorithme en fonction de la taille et des caractéristiques de l’entrée permet de concevoir des solutions plus efficaces et adaptatives.
Cette complexité utilise les mêmes notations asymptotiques que celles présentées dans la partie complexité temporelle. Nous allons donc présenter dans cette partie du cours la complexité spatiale qui est décomposé en deux mémoires. La mémoire spatiale de stockage des données en entrées, et la mémoire spatiale auxiliaire que les différentes opérations engendrent durant l’algorithme.
La mémoire spatiale des données en entrée
Selon les données en entrée du problème, il faut les stocker durant la totalité de l’algorithme. Un espace mémoire est donc alloué pour conserver les différentes données qu’elles soient primitives comme des entiers, booléen ou un caractère, mais aussi des structures de données linéaire comme des listes avancées. L’objectif de la complexité spatiale (ou complexité mémoire) réside dans le comptage des cases mémoires allouées.
Dans le tableau suivant, le terme “élément” fait référence à une variable primitive, pour simplifier l’analyse. En pratique, la taille d’un élément peut varier en fonction du type de données et de l’implémentation spécifique.
| Type de donnée | Exemple | Taille de la donnée | Complexité spatiale |
|---|---|---|---|
| Variable primitive | int, float, bool, char |
constante | O(1) |
| Liste / Ensemble | [1, 2, 3, ..., n] |
n éléments | O(n) |
| Chaîne de caractères | "bonjour" |
liste de n char |
O(n) |
| Liste de listes (matrice) | [[...], [...], ...] (m lignes, p colonnes) |
m × p éléments | O (m·p) |
| Dictionnaire | {clé: valeur} avec n paires |
2n éléments | O(n) |
| Arbre binaire | n noeuds reliés | chaque noeud = 1 élément + pointeurs | O(n) |
| Graphe (liste d’adjacence) | adj[v] = liste des voisins de v |
n sommets, m arêtes | O(n + m) |
Il est à noté que cette mémoire est souvent négligée dans la complexité spatiale totale car elle est considérée comme déjà donnée par les paramètres en entrée. Mais nous verrons en fin de cours qu’elle peut être très importante dans des cas réels.
La mémoire spatiale auxiliaire
C’est la mémoire spatiale importante dans l’analyse d’un algorithme. Car il faut prendre en compte la création de toute variable en mémoire et des coûts mémoires des différents processus.
-
Lorsque la complexité spatiale vaut $O(1)$, c’est que la taille mémoire utilisée ne dépend pas de $n$. Par exemple l’initialisation d’une variable entière, ou faire une boucle itérative simple.
-
Lors de la création de tableaux temporaires à une ($n$) ou plusieurs dimensions ($n*m$), nous obtenons $O(n)$ ou $O(n^2)$
-
Lorsque nous utilisons une pile récursive (par exemple dans une fonction récursive simple), la taille de la pile utilise de la mémoire en attendant les résultats récursifs. Dans ces cas là, la complexité dans le pire des cas est la taille maximum de la pile durant le déroulé de l’algorithme (nombre de niveaux d’appels). C’est donc généralement en $O(n)$. Reprenons l’exemple donné dans le cours d’algorithme 2 avec factoriel(3) :
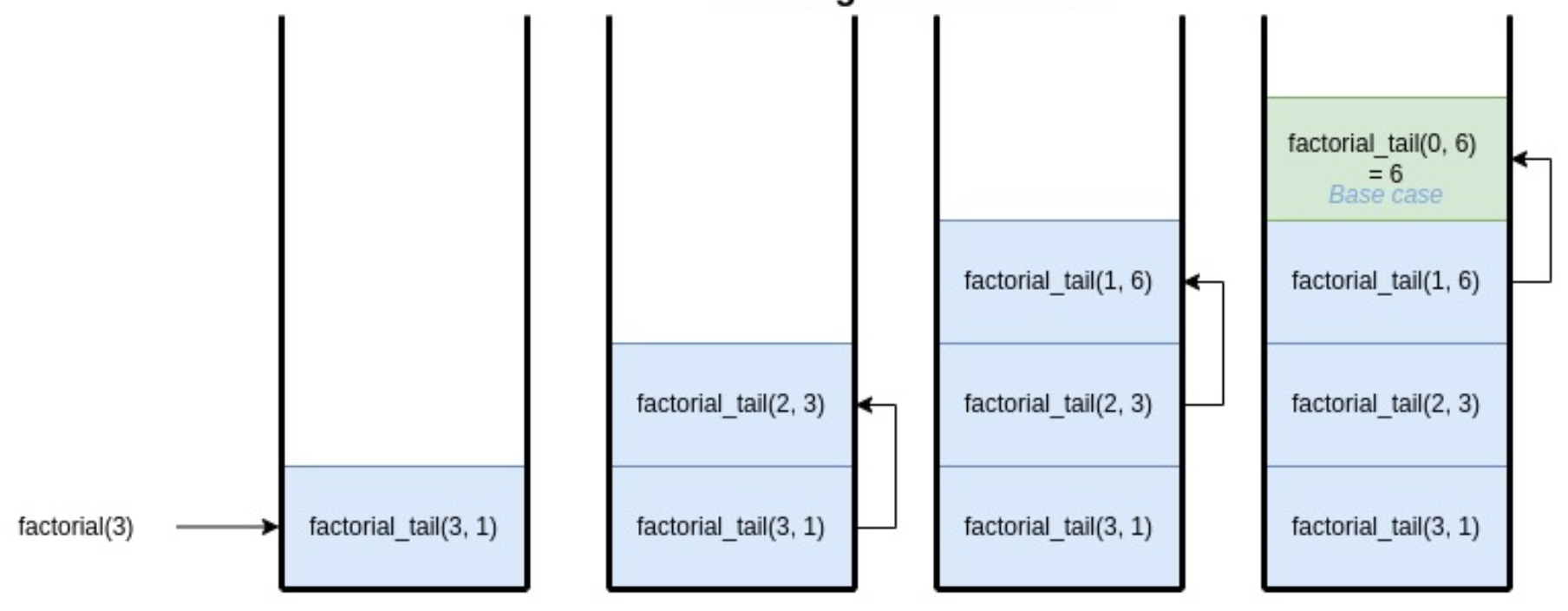 |
|---|
Pile d’appels pour factorial_tail(n,m). |
La pile atteint une hauteur de 3 appels récursifs et le quatrième (base) retourne immédiatement le résultat au niveau en dessous.
- Le stockage de résultats intermédiaires et ré-utilisables prennent également de la place mémoire. Mais ces choix d’augmentation de la mémoire auxiliaire servent souvent à réduire le temps de calcul. C’est le cas pour les processus de mémoïsation ou de programmation dynamique. Ces notions seront détaillées et étudiées dans le cours d’algorithme 4. Les complexités spatiales auxiliaires nécessaires peuvent alors varier entre $O(log(n))$ et $O(2^n)$ selon les problèmes.
2 — Analyse de la complexité spatiale d’algorithmes
a - Un exemple simple
Regardons sur cet exemple comment évaluer le coût de la méthode func(liste_n_elements).
def func(liste_n_elements : list[int]):
i = 0
res = 0
for i in range(len(liste_n_elements)) :
res += liste_n_elements[i]
return resAnalysons la mémoire des données en entrée requise :
- Stocker la liste liste_n_elements demande n cases mémoires unitaires $\rightarrow O(n)$
Analysons la mémoire auxiliaire requise :
- Initialiser les variables
ietresdemande deux cases mémoires unitaires $\rightarrow O(2)$ - La boucle for n’engendre pas plus d’espace mémoire, nous gardons la taille allouée pour la liste et pour les deux variables
ietres. $\rightarrow O(1)$ - Retourner la variable
resne coût rien de plus en mémoire. $\rightarrow O(1)$
Cet algorithme a donc une complexité spatiale totale égale à :
$$ \text{Complexité spatiale totale }= \text{Complexité spatiale en entrée} + \text{Complexité spatiale auxiliaire} $$ $$ \text{Complexité spatiale totale }= O(n) + O(2) = O(n) $$b - Exemple avancé avec la fonction $a^n$
L’idée est de présenter un problème simple où différent algorithmes illustrent la relation entre temps et espace, et comment parfois réduire l’un ne fait pas forcément monter l’autre.
On va donc construire cinq versions du même algorithme :
- Version itérative : lente et peu gourmande en mémoire
- Version récursive simple : lente mais coûte plus d’espace
- Version récursive rapide : rapide mais coûte plus d’espace
- Version récursive rapide avec stockage : rapide et peu d’espace
- Version optimisée : rapide et sans espace
Version itérative — linéaire
def Puissance_Lente(a, n) :
resultat = 1
for i in range(1,n) :
resultat = resultat * a
return resultatChaque multiplication se fait séquentiellement. Aucun stockage intermédiaire $\rightarrow O(1)$ mémoire auxiliaire.
Complexité temporelle : $ O(n)$
Complexité spatiale auxiliaire : $O(1)$
Version récursive simple - linéaire
def puissance_rec(a, n) :
if n == 0:
return 1
return a * puissance_rec(a, n - 1)Chaque multiplication se fait récursivement via une pile d’appels. Stockage intermédiaire avec la pile $\rightarrow O(n)$ mémoire auxiliaire.
Complexité temporelle : $ O(n)$
Complexité spatiale auxiliaire : $O(n)$
Version récursive rapide - logarithmique
Cette version se base sur le fait que $a^{2p} = a^p*a^p $, et où il suffit de calculer une seule fois $a^p $ divisant ainsi les calculs par deux. Cette méthode de calcul s’appelle diviser pour régner et sera plus profondément étudié dans le cours algorithme 4
def puissance_rapide(a, n) :
if n == 0:
return 1
if n == 1:
return a
if n % 2 == 0:
return puissance_rapide(a, n // 2) * puissance_rapide(a, n // 2)
else:
return a * puissance_rapide(a, n // 2) * puissance_rapide(a, n // 2) Chaque produit des puissances divisées par 2 se fait récursivement via une pile d’appels. Stockage intermédiaire avec la pile $\rightarrow O(log(n))$ mémoire auxiliaire. La pile est moins profonde (car divisé par 2), mais l’on calcule deux fois chaque récurrence (aucun gain temporel).
Complexité temporelle : $ O(n)$
Complexité spatiale auxiliaire : $O(log(n))$
Version récursive rapide avec stockage - logarithmique
Cette version est une optimisation simple de la précédente où nous stockons le résultat de la récurrence dans une variable.
def puissance_rapide_stock(a, n) :
if n == 0:
return 1
if n == 1:
return a
demi = puissance_rapide_stock(a, n // 2)
if n % 2 == 0:
return demi * demi
else:
return a * demi * demi Même stockage intermédiaire avec la pile $\rightarrow O(log(n))$ mémoire auxiliaire. Mais un seul calcul par récurrence !
Complexité temporelle : $ O(log(n))$
Complexité spatiale auxiliaire : $O(log(n))$
Dans le cas de cet exemple, il n’est pas nécessaire de garder à long terme en mémoire chaque calcul récursif, il est simplement stocké dans une variable locale demi. Mais il peut être intéressant pour d’autres types de problèmes de re-utiliser les mêmes calculs durant les appels récursifs. Ça sera justement le cas pour l’algorithme de Fibonacci, lors du cours algorithme 4 vous verrez l’utilisation de la mémoïsation pour accélérer les calculs.
Version optimisée en temps et en espace
On peut profiter de la même décomposition rapide mais en la rendant itérative pour supprimer la pile récursive.
def Puissance_Optimisee(a, n) :
resultat= 1
base= a
exposant = n
while exposant > 0 :
if exposant %2 == 1 :
resultat = resultat * base
base = base * base
exposant = exposant // 2
return resultatAnalyse :
La boucle se répète environ $log(n)$ fois. Aucune pile n’est utilisée.
Complexité temporelle : $O(log(n))$
Complexité spatiale auxiliaire : $O(1)$
| Version | Principe | Temps | Mémoire auxiliaire | Commentaire |
|---|---|---|---|---|
Puissance_Lente |
Multiplication répétée | $O(n)$ | $O(1)$ | Simple, lente |
Puissance_Rec |
Récursive | $O(n)$ | $O(n)$ | lente et plus lourde |
Puissance_rapide |
Récursive + division des opérations | $O(n)$ | $O(log(n))$ | lente et plus légère |
Puissance_rapide_stockage |
Récursive + division des opérations + stockage | $O(log(n))$ | $O(log(n))$ | Rapide et plus légère |
Puissance_Optimisee |
Itérative + division des opérations | $O(log(n))$ | $O(1)$ | Idéale |
Afin de jouer avec les différents algorithmes et voir leur efficacité, vous pouvez copier/coller les algorithmes dans un même fichier python et y ajouter le code suivant :
import time
import tracemalloc
from typing import Callable
# --- pensez à ajouter les différents algorithmes
def mesurer_perf(fonction: Callable[[float, int], float], a: float, n: int) -> None:
tracemalloc.start()
t0 = time.perf_counter()
resultat = fonction(a, n)
t1 = time.perf_counter()
mem_courante, mem_pic = tracemalloc.get_traced_memory()
tracemalloc.stop()
print(f"--- {fonction.__name__} ---")
print(f"Résultat = {resultat}")
print(f"Temps d’exécution : {t1 - t0:.6f} s")
print(f"Pic de mémoire utilisée : {mem_pic / 1024:.2f} Ko")
print("---------------------------\n")
# --- Test comparatif ---
if __name__ == "__main__":
a, n = 2.0, 1000
print(f"Comparaison pour a = {a}, n = {n}\n")
mesurer_perf(puissance_lente, a, 20) # petite valeur sinon stack overflow
mesurer_perf(puissance_rec, a, 20) # petite valeur sinon stack overflow
mesurer_perf(puissance_rapide, a, n)
mesurer_perf(puissance_rapide_stock, a, n)
mesurer_perf(puissance_optimisee, a, n)3 - Cas pratiques - temps vs mémoire :
En pratique, les mêmes problèmes peuvent être résolus de manière complètement différentes selon les contraintes imposées et le contexte. Le choix d’optimiser la rapidité d’un algorithme au détriment de la mémoire utilisée peut se justifier, tout comme son inverse. Présentons quelques cas pratiques.
La taille des données
Si les données tiennent facilement en mémoire :
- on peut se permettre d’utiliser des structures supplémentaires pour gagner du temps. Ex : Indexer un tableau dans une table de hachage pour des recherches plus rapides.
- on peut mettre en place des mécanismes plus lourd en mémoire pour réduire le temps.
Si les données sont volumineuses selon le contexte (big data, en embarqué) :
- Il faut minimiser l’espace auxiliaire, quitte à accepter plus de calculs. Ex : Tri externe (utilise peu de mémoire, mais plus lent car nécessite des lectures disque).
- on peut recalculer plusieurs fois les mêmes résultats pour ne pas avoir à les stocker.
Le nombre d’opérations répétées
Si le calcul est répété plusieurs fois avec les mêmes sous-problèmes $\rightarrow$ mémoïsation très rentable.
Si le calcul est exécuté une seule fois, la mémorisation est inutile $\rightarrow$ on privilégie une version sans stockage.
Les contraintes du système
En environnement embarqué / microcontrôleurs : Mémoire très limitée $\rightarrow$ algorithmes spatiaux efficaces, même s’ils sont plus lents.
Sur serveur ou GPU : Mémoire disponible, priorité à la vitesse $\rightarrow$ pré-calcul, stockage intermédiaire.
4 - Exemple concret - Navigation automobile avec GPS embarqué
Un GPS embarqué doit calculer des itinéraires sur un graphe de plusieurs millions de routes. Mais il dispose de 256 Mo de RAM seulement.
Solution rapide mais coûteuse en mémoire (Dijkstra) :
Une première solution charge tout le graphe en mémoire et utilise une file de priorité avec les distances. On ne cherche à calcule qu’une fois mais la carte prend toute la mémoire et le programme sature.
- Temps : $O((n+m)* log(n))$
- Espace : $O(n)$ stocke toutes les distances et la file $\rightarrow$ mémoire vite saturée
Solution lente mais légère en mémoire (Recherche segmentée) :
Une autre solution qui prend plus de temps. On découpe la carte en zones, puis charge une seule portion du graphe à la fois. Cela va demander de re-executer plusieurs fois Dijkstra et de mixer les résultats.
- Temps : bien plus lent, mais dur à calculer car cela dépend de la segmentation et du nombre de fois qu’il faut recalculer Dikjstra par zone.
- Espace : $O(\sqrt{n})$, ou une complexité encore plus basse.
Pour aller encore plus loin
Lien extérieur vers les structures de données en Python