Diviser pour régner
Temps de lecture20 minEn bref
Résumé de l’article
Cet article explore la stratégie diviser pour régner en informatique, retraçant ses racines historiques et expliquant son application dans la conception d’algorithmes. Il décrit les trois étapes principales : diviser, conquérir et combiner, et discute des inefficacités qui surviennent avec les sous-problèmes qui se chevauchent.
L’article introduit également la mémoïsation et la programmation dynamique comme techniques pour optimiser les algorithmes récursifs, en utilisant la suite de Fibonacci comme étude de cas. Il couvre aussi les problèmes d’optimisation et le problème du rendu de monnaie, démontrant comment la programmation dynamique et les algorithmes gloutons peuvent être appliqués. L’article se conclut par une comparaison de ces approches et de leurs compromis.
Points clés à retenir
-
La stratégie diviser pour régner implique de diviser un problème en sous-problèmes plus petits, de les résoudre indépendamment, puis de combiner leurs solutions pour résoudre le problème original.
-
Les techniques de mémoïsation et de programmation dynamique peuvent optimiser les algorithmes récursifs en évitant les calculs redondants de sous-problèmes qui se chevauchent.
-
La programmation dynamique garantit des solutions optimales en considérant toutes les possibilités de solutions.
-
Choisir la bonne approche algorithmique (récursive, mémoïsée, ou programmation dynamique) basée sur les caractéristiques du problème est essentiel pour une résolution efficace des problèmes.
Contenu de l’article
1 — Diviser pour régner
La maxime “Diviser pour régner” a pris des formes très différentes au fil du temps et a été utilisée à de nombreuses occasions politiques avant d’être utilisée en informatique. Son origine peut être attribuée à Philippe II de Macédoine, comme “Διαίρει καὶ βασίλευε” (Diaírei kaì basíleue) en grec, littéralement “diviser et régner”. Que ce soit en politique ou en science, il est en effet plus facile de maîtriser un problème complexe quand il peut être divisé en sous-problèmes plus petits et plus simples.
Résoudre algorithmiquement un problème en utilisant une stratégie diviser pour régner nécessite trois étapes :
- Diviser – Le problème est divisé (ou décomposé) en sous-problèmes plus petits.
- Conquérir – Chacun des sous-problèmes est résolu indépendamment.
- Combiner : Les solutions des sous-problèmes sont combinées (ou composées) pour produire la solution au problème initial.
L’étape Conquérir peut nécessiter à son tour d’appliquer une stratégie diviser pour régner spécifique, car les sous-problèmes sont d’une autre nature que le problème initial. Quand on examine des problèmes de base, les sous-problèmes sont cependant typiquement de même nature que le problème initial, seulement plus petits (ceci pourrait en fait être utilisé comme définition d’un problème de base). De tels problèmes peuvent être définis récursivement et directement implémentés comme des fonctions récursives. Vous avez précédemment vu quelques exemples de tels problèmes avec leur implémentation récursive dans la session 2.
Dans ce cours, nous allons considérer des cas spécifiques où les mêmes instances de (sous-)problèmes se produisent plusieurs fois lors de la résolution d’une instance de problème donnée. Le problème initial est dit avoir des sous-problèmes qui se chevauchent. Dans un tel cas, une implémentation directe de la définition récursive du problème peut être terriblement inefficace car les mêmes instances de sous-problèmes sont résolues encore et encore.
Il y a deux techniques de base pour éviter cette redondance : la mémoïsation et la programmation dynamique. Nous allons voir comment ces techniques s’appliquent aux problèmes à solution unique, c’est-à-dire les problèmes qui ne sont ni des problèmes de recherche ni des problèmes d’optimisation (voir l’article sur les problèmes).
Dans la littérature, le terme “diviser pour régner” est parfois utilisé seulement quand les sous-problèmes sont non-chevauchants.
2 — Problèmes à solution unique
2.1 — Les nombres de Fibonacci
Expliquons le principe de décomposition de problème en examinant les nombres de Fibonacci. Cette suite était déjà utilisée très tôt par les mathématiciens indiens comme moyen d’énumérer les motifs de poésie sanskrite. Elle doit son nom au mathématicien italien Leonardo de Pise, appelé plus tard Fibonacci, qui a introduit la suite dans son Livre de calcul (1202). Le nombre de Fibonacci $F_n$ donne, à la fin du mois $n$, la taille d’une population idéalisée de lapins qui se comporte comme suit :
- Initialement, une première paire reproductrice de lapins est mise dans un champ.
- Une paire reproductrice de lapins s’accouple quand elle a un mois et produit une nouvelle paire de lapins un mois plus tard. Une fois qu’elle est mature, elle le fait chaque mois.
Voici une illustration de comment la population évolue pendant les six premiers mois :
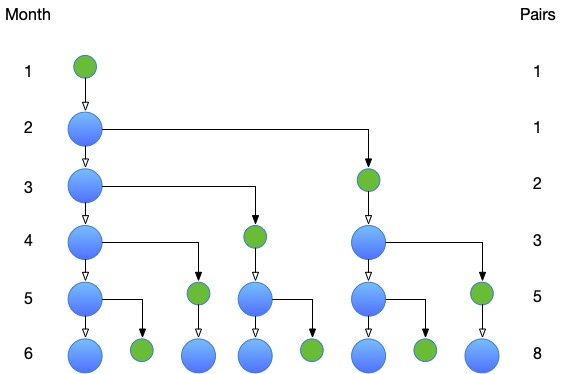
À la fin du premier mois, il n’y a qu’une seule paire reproductrice, $F_1 = 1$. À la fin du deuxième mois, il n’y a encore qu’une seule paire reproductrice, $F_2 = 1$, mais cette paire reproductrice est mature, et a produit, à la fin du troisième mois, une nouvelle paire reproductrice, $F_3 = 2$.
Plus généralement, à la fin du mois $n$, il y a les paires reproductrices qui étaient là à la fin du mois précédent, ainsi que les nouvelles paires reproductrices produites par les paires matures, c’est-à-dire les paires reproductrices qui étaient là deux mois auparavant. Cela donne $F_n = F_{n-1} + F_{n-2}$. La suite peut être complétée avec $F_0 = 0$, auquel cas $F_n = F_{n-1} + F_{n-2}$ est déjà vrai pour $n = 2$.
En résumé, les nombres de Fibonacci peuvent être définis par la relation de récurrence : $F_0 = 0$, $F_1 = 1$, et $F_n = F_{n-1} + F_{n-2}$.
2.2 — La version récursive
Ceci peut facilement être implémenté en Python :
# Required to measure the time taken by the program
import time
from typing import Callable
def fib (n: int) -> int:
"""
The Fibonacci numbers are defined by the recurrence relation F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}.
This function computes F_n.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Base cases
if n == 0:
return 0
if n == 1:
return 1
# Recursive case
return fib(n - 1) + fib(n - 2)
def time_call (f: Callable, n: int) -> None:
"""
This function measures the time taken by the function f to compute f(n) and prints the result.
In:
* f: A function to measure.
* n: An integer.
Out:
None
"""
start = time.perf_counter()
print(f'{f.__name__}({n}) = {f(n)}')
elapsed = time.perf_counter() - start
print(f'Time taken: {elapsed:.6f} seconds')
# Test cases
time_call(fib, 10) # 55
time_call(fib, 20) # 6765
time_call(fib, 40) # 832040import java.util.function.IntFunction;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
}
}Malheureusement, la complexité du programme est exponentielle en temps.
Cela peut être vu expérimentalement en chronométrant le programme (avec la fonction time_call dans l’illustration) ainsi que théoriquement en calculant le temps d’exécution $T(n)$ du programme :
En notant que :
$$T(n) \geq T(n-1) + T(n-2) \geq 2T(n-2) \geq 2^n(n-4) \geq ... \geq 2^{n/2} T(0) = 2^{n/2}$$En pratique, dessiner l’arbre d’appels de, par exemple, fib(5) montre que chaque appel est en fait répété un nombre croissant de fois à mesure que la taille du sous-problème diminue :
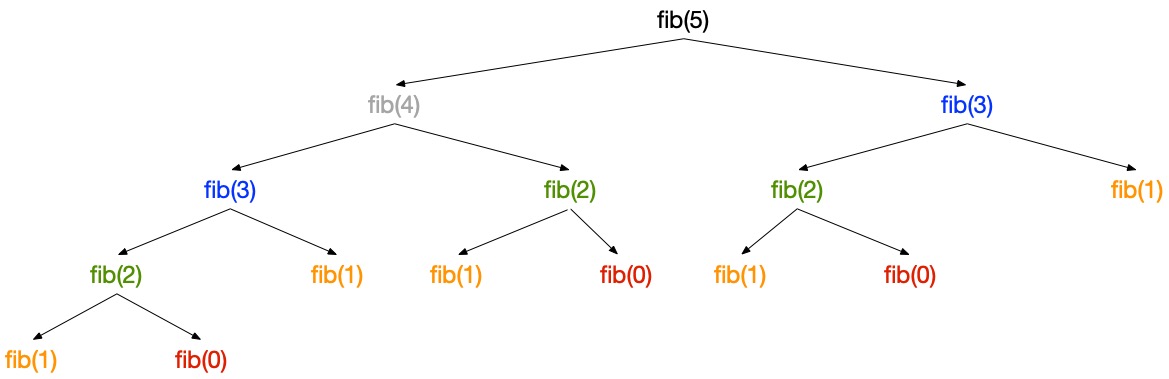
L’arbre d’appels donne aussi l’intuition que le programme est linéaire en espace. Chaque appel pousse un enregistrement d’activation sur la pile d’appels et le retire quand il retourne. La taille maximale de la pile correspond à la profondeur maximale de l’arbre d’appels. Un appel à $fib(n)$ pousse au plus $n$ enregistrements d’activation sur la pile.
Une étude complète de la complexité de fib nécessiterait d’examiner la complexité de l’addition de grands entiers, qui ne prend pas un temps constant.
2.3 — La version mémoïsée
L’observation que presque tous les appels sont calculés de manière répétée conduit à l’idée de mémoïsation. Que diriez-vous de construire un mémo (d’où le terme mémoïsation) enregistrant les résultats des appels rencontrés afin de les réutiliser plus tard ?
Un mémo pour une fonction $f$ de type $E \rightarrow S$ peut être implémenté comme un dictionnaire de paires $(key, value)$, où $key$ est un élément de $E$ et $value$ est simplement égal à $f(key)$. Quand un appel $f(e)$ est rencontré, soit $e$ est une clé dans le dictionnaire et la valeur correspondante est retournée, soit il n’y a pas une telle clé, $f(e)$ est calculé, $(e, f(e))$ est ajouté au dictionnaire, et $f(e)$ est retourné. Notez que si $f$ a plusieurs paramètres, c’est-à-dire, $E$ a la forme $E_1 \times...\times E_n$, alors les clés sont des tuples de paramètres.
Dans le cas de Fibonacci, le paramètre est un entier, il est possible de réduire le dictionnaire à un tableau, qui doit être initialisé avec une valeur invalide (par exemple -1), permettant de distinguer entre les valeurs déjà calculées et les valeurs encore à calculer.
Voici l’implémentation correspondante en Python :
def fib_memo (n):
"""
This function computes the n-th Fibonacci number using memoization.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Initialization of memo
memo = [-1 for _ in range(n + 1)]
# Inner auxiliary function to recursively define Fibonacci and hide memoization from the user
def __fib_memo (n):
"""
This function computes recursively the n-th Fibonacci number using memoization.
In:
* n: an integer.
Out:
* The n-th Fibonacci number.
"""
# If the result has already been computed, return it
if memo[n] != -1:
return memo[n]
# Otherwise, standard computation (see earlier)
if n == 0:
result = 0
elif n == 1:
result = 1
else:
result = __fib_memo(n - 1) + __fib_memo(n - 2)
# Record the result in memo
memo[n] = result
return result
# Call the inner function
return __fib_memo(n)
# Test cases
time_call(fib_memo, 10) # 55 # cold start
time_call(fib_memo, 10) # 55 # warm start
time_call(fib_memo, 20) # 6765
time_call(fib_memo, 40) # 832040
time_call(fib_memo, 80) # 23416728348467685
time_call(fib_memo, 160) # 47108659444709974473273497672572071429
time_call(fib_memo, 320) # ...import java.util.function.IntFunction;
import java.util.Arrays;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static int fibMemo(int n) {
int[] memo = new int[n + 1];
Arrays.fill(memo, -1);
return fibMemoAux(n, memo);
}
private static int fibMemoAux(int n, int[] memo) {
if (memo[n] != -1) {
return memo[n];
}
if (n == 0) {
memo[n] = 0;
} else if (n == 1) {
memo[n] = 1;
} else {
memo[n] = fibMemoAux(n - 1, memo) + fibMemoAux(n - 2, memo);
}
return memo[n];
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
System.out.println("fibo memo");
// Test cases
timeCall(FibboInit::fibMemo, 10); // 55 # cold start
timeCall(FibboInit::fibMemo, 10); // 55 # warm start
timeCall(FibboInit::fibMemo, 20); // 6765
timeCall(FibboInit::fibMemo, 40); // 832040
timeCall(FibboInit::fibMemo, 80); // 23416728348467685
timeCall(FibboInit::fibMemo, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibMemo, 320); // ...
}
}Ici memo est défini comme local à la fonction fib_memo.
Il pourrait aussi être défini comme une variable globale afin d’être partagé à travers différents appels à fib_memo.
Quand on utilise un tableau pour la mémoïsation, la taille du tableau doit être connue à l’avance. Cela peut être problématique si la taille maximale de l’entrée n’est pas connue ou si la taille de l’entrée peut varier significativement. De plus, les tableaux sont moins flexibles comparés à d’autres structures de données comme les dictionnaires. Par exemple, si le domaine d’entrée est clairsemé ou non-contigu, utiliser un tableau peut conduire à un gaspillage d’espace. Les dictionnaires, d’autre part, peuvent croître dynamiquement et n’utilisent de la mémoire que pour les clés qui sont effectivement nécessaires.
La complexité temporelle du programme est maintenant linéaire. Il y a cependant un compromis temps-espace : plus d’espace est utilisé. Dans le cas de Fibonacci, cet espace supplémentaire, au moins quand on utilise un tableau, est proportionnel à l’argument. La complexité spatiale est donc inchangée.
En général, quand la version récursive d’un problème prend un temps exponentiel, la version de programmation dynamique prend un temps polynomial, mais cela nécessite que le nombre de sous-problèmes distincts soit polynomial par rapport à la taille du problème.
2.4 — Programmation dynamique
Quand on utilise soit la récursivité soit la mémoïsation, l’exécution procède de manière descendante : en commençant par le problème avec la plus grande taille, elle résout les sous-problèmes de tailles plus petites afin de finalement résoudre le problème initial. Mais il est aussi possible de procéder dans l’autre sens, c’est-à-dire, ascendante.
La notion de taille de problème est clé. Elle rend possible de trier les problèmes par rapport à leur taille. Si résoudre un problème ne repose que sur la résolution de sous-problèmes plus petits, il est alors possible de résoudre les problèmes en commençant par leurs sous-problèmes plus petits (à n’importe quelle profondeur) et en procédant avec des problèmes plus grands jusqu’à ce que le problème initial soit résolu.
Tout au long, les solutions sont mémoïsées, c’est-à-dire, enregistrées dans un mémo. Quand un problème est sur le point d’être résolu, tous ses sous-problèmes ont donc déjà été résolus par conception.
Quand on applique cela à fib$(n)$, les plus petits problèmes, fib(0) et fib(1) sont (trivialement) résolus en premier, et le calcul procède avec fib(2), fib(3)… jusqu’à ce que fib$(n)$ soit atteint.
Pourquoi cela s’appelle-t-il programmation dynamique ? Eh bien, cela n’a pas grand-chose à voir avec la programmation (en Python ou tout autre langage de programmation), mais plutôt avec la planification (construire des plans) et cette planification n’est pas dynamique (elle n’arrive pas quand le programme s’exécute) mais statique (c’est quand nous programmons que nous faisons la planification). (voir l’article Wikipedia sur la programmation dynamique).
Parfois, la mémoïsation est classifiée comme programmation dynamique descendante.
2.4.1 — Le graphe des sous-problèmes
Résoudre un problème en utilisant la programmation dynamique nécessite de comprendre comment le problème est structuré en termes de ses sous-problèmes et de leurs dépendances. Ceci est représenté par le graphe des sous-problèmes, plus précisément un graphe orienté acyclique. Chaque sommet correspond à un problème avec des arêtes pointant vers les problèmes dont il dépend directement (ce sont des sous-problèmes, pas des sous-sous…problèmes). Cela correspond à une sorte de version “compactée” de l’arbre d’appels de la version récursive, où tous les nœuds avec les mêmes étiquettes sont fusionnés.
Voici à quoi ressemble le graphe de problème pour fib(5) :
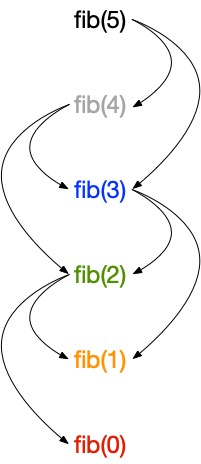
Trier les sommets en utilisant un tri topologique inverse donne l’ordre dans lequel les sous-problèmes doivent être résolus.
Fondamentalement, un sommet n’est sélectionné que si les sommets dont il dépend ont déjà été sélectionnés.
En termes de problèmes et sous-problèmes, cela correspond à l’idée qu’un problème ne peut être résolu que si ses sous-problèmes (directs) ont déjà été résolus.
Dans le cas de fib, le calcul devrait commencer par fib(0), puis fib(1), fib(2)… fib($n$) pour tout $n$.
Le graphe peut être utilisé pour déterminer le temps d’exécution de l’algorithme.
Puisque chaque sous-problème n’est résolu qu’une seule fois, le coût total est la somme des temps nécessaires pour résoudre chaque sous-problème.
Le temps pour calculer un sous-problème est typiquement proportionnel au degré (le nombre d’arêtes sortantes) du sommet correspondant.
En supposant que le degré ne varie pas avec la taille du problème, le temps d’exécution d’un algorithme utilisant la programmation dynamique est typiquement linéaire en le nombre de sommets et d’arêtes.
Dans le cas de fib$(n)$, il y a exactement $n$ sommets.
Le temps d’exécution est linéaire en $n$.
2.4.2 — Le programme
Maintenant que nous comprenons comment “planifier” les calculs, nous pouvons écrire un programme calculant les nombres de Fibonacci avec la programmation dynamique :
def fib_dp (n):
"""
This function computes the n-th Fibonacci number using dynamic programming.
In:
* n: An integer.
Out:
* The n-th Fibonacci number.
"""
# Initialization of memo
memo = [0 for _ in range(n + 1)]
memo[1] = 1
# Exploit previous memoized results
# i.e., i in [2, n+1[ (or [2, n])
for i in range(2, n + 1):
memo[i] = memo[i - 1] + memo[i - 2]
return memo[n]
# Test cases
time_call(fib_dp, 10) # 55 # cold start
time_call(fib_dp, 10) # 55 # warm start
time_call(fib_dp, 20) # 6765
time_call(fib_dp, 40) # 832040
time_call(fib_dp, 80) # 23416728348467685
time_call(fib_dp, 160) # 47108659444709974473273497672572071429
time_call(fib_dp, 320) #import java.util.function.IntFunction;
import java.util.Arrays;
public class FibboInit {
public static int fib(int n) {
// Base cases
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// Recursive case
return fib(n - 1) + fib(n - 2);
}
public static int fibMemo(int n) {
int[] memo = new int[n + 1];
Arrays.fill(memo, -1);
return fibMemoAux(n, memo);
}
private static int fibMemoAux(int n, int[] memo) {
if (memo[n] != -1) {
return memo[n];
}
if (n == 0) {
memo[n] = 0;
} else if (n == 1) {
memo[n] = 1;
} else {
memo[n] = fibMemoAux(n - 1, memo) + fibMemoAux(n - 2, memo);
}
return memo[n];
}
public static int fibDp(int n) {
int[] memo = new int[n + 1];
memo[1] = 1;
for (int i = 2; i <= n; i++) {
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
}
public static void timeCall(IntFunction<Integer> f, int n) {
long start = System.nanoTime();
System.out.println(f.apply(n));
long elapsed = System.nanoTime() - start;
System.out.printf("Time taken: %.6f seconds%n", elapsed / 1e9);
}
public static void main(String[] args) {
// Test cases
timeCall(FibboInit::fib, 10); // 55
timeCall(FibboInit::fib, 20); // 6765
timeCall(FibboInit::fib, 40); // 832040
System.out.println("fibo memo");
// Test cases
timeCall(FibboInit::fibMemo, 10); // 55 # cold start
timeCall(FibboInit::fibMemo, 10); // 55 # warm start
timeCall(FibboInit::fibMemo, 20); // 6765
timeCall(FibboInit::fibMemo, 40); // 832040
timeCall(FibboInit::fibMemo, 80); // 23416728348467685
timeCall(FibboInit::fibMemo, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibMemo, 320); // ...
System.out.println("dynamic programming");
// Test cases
timeCall(FibboInit::fibDp, 10); // 55 # cold start
timeCall(FibboInit::fibDp, 10); // 55 # warm start
timeCall(FibboInit::fibDp, 20); // 6765
timeCall(FibboInit::fibDp, 40); // 832040
timeCall(FibboInit::fibDp, 80); // 23416728348467685
timeCall(FibboInit::fibDp, 160); // 47108659444709974473273497672572071429
timeCall(FibboInit::fibDp, 320); // ...
}
}2.5 — Prenons du recul
Vous pouvez vérifier expérimentalement que la version utilisant la programmation dynamique s’exécute plus rapidement que la version utilisant la mémoïsation.
Elle utilise aussi moins de mémoire (memo utilise la même quantité de mémoire tas dans les deux versions et la pile est utilisée pour un seul enregistrement d’activation correspondant à l’appel initial).
Cependant, nous avons gagné beaucoup plus entre la version initiale et la version mémoïsée (d’une complexité exponentielle à linéaire) qu’entre la version mémoïsée et la version de programmation dynamique (un facteur constant).
De plus, la version de programmation dynamique nécessite plus de travail et est plus sujette aux erreurs.
Il y a un écart plus grand entre la spécification du problème et la programmation de sa solution.
En conséquence, il est souvent une bonne idée de passer par toutes les étapes, c’est-à-dire, produire la version récursive, la version mémoïsée, et finalement la version de programmation dynamique, seulement si la version mémoïsée n’est pas suffisamment efficace. Dans le cas où la version de programmation dynamique est requise, la version mémoïsée est encore utile pour tester efficacement la correction de la version de programmation dynamique.
Pour aller plus loin
Il semble que cette section soit vide !
Y a-t-il quelque chose que vous auriez aimé voir ici ? Faites-le nous savoir sur le serveur Discord ! Peut-être pouvons-nous l’ajouter rapidement. Sinon, cela nous aidera à améliorer le cours pour l’année prochaine !
Pour aller encore plus loin
- Équation de Bellman.
La programmation dynamique repose sur un principe théorique étudié par Richard Bellman qui se rapporte à une équation entre la solution optimale d’un problème et une combinaison de solutions optimales pour certains de ses sous-problèmes. Pour les plus curieux d’entre vous, jetez un œil à ce contexte théorique.