De l'optimisation aux approches approximatives

En bref

Résumé de l’article

Cet article couvre les problèmes d’optimisation et le problème du rendu de monnaie, démontrant comment la programmation dynamique et les algorithmes gloutons peuvent être appliqués. Nous discutons également de la façon dont une heuristique gloutonne peut être utilisée pour approximer une solution à ce problème. L’article se conclut par une comparaison de ces approches et de leurs compromis.

Points clés à retenir

• Trouver des solutions exactes aux problèmes d’optimisation peut être très coûteux, même avec la programmation dynamique.

• Les algorithmes gloutons peuvent donner une solution proche de l’optimum en optimisant localement une fonction de manière itérative au lieu d’une fois globalement.

• Parfois, les algorithmes gloutons peuvent fournir des solutions exactes, mais pas toujours !

Contenu de l’article

1 — Problèmes d’optimisation

La programmation dynamique est souvent très utile pour traiter les problèmes d’optimisation (voir la note sur les problèmes). Le point important est que les problèmes d’optimisation sont des variantes de problèmes de recherche avec de nombreuses solutions. Intuitivement, si le calcul naïf d’une solution implique déjà de nombreux recalculs, cela va être pire lors de la recherche de la meilleure solution.

Résoudre un problème d’optimisation en utilisant la programmation dynamique nécessite de suivre les mêmes étapes qu’auparavant, avec la contrainte que le problème d’optimisation doit présenter une propriété supplémentaire : il doit présenter une sous-structure optimale.

Qu’est-ce que cela signifie ? Pour appliquer correctement une stratégie diviser pour régner, nous devons être capables de décomposer les problèmes en sous-problèmes et de composer les solutions des sous-problèmes en une solution au problème. Comme nous voulons produire des solutions optimales, nous devons nous assurer qu’en composant les solutions optimales des sous-problèmes, nous obtenons bien la solution optimale au problème. De plus, comme il y a un problème de recherche sous-jacent, il y a des choix. Un choix peut être vu comme un nouveau type de décomposition où le choix est divisé en ses différentes alternatives. Son coût est alors le minimum des coûts de ses alternatives.

Voyons comment cela fonctionne avec le problème du rendu de monnaie.

2 — Le problème du rendu de monnaie

Ce problème est une variante du problème du change de monnaie que vous avez rencontré précédemment. Les paramètres d’entrée sont les mêmes :

• Une liste de valeurs entières donnant les dénominations des pièces et billets disponibles dans la devise, par exemple [1, 2, 5, 10, 50] pour les euros. Nous supposons ici que ces valeurs $v_1$, …, $v_n$ sont ordonnées : $v_1 \lt ... \lt v_n$.
• Un montant à changer.

Mais, alors que le problème du change de monnaie cherche le nombre de façons de changer le montant, le problème du rendu de monnaie cherche le nombre minimum de pièces nécessaires.

2.1 — Le problème du change de monnaie

Voici un code possible pour le problème du change de monnaie :

def count_coin_changes (amount: int, coins: list[int]) -> int:
    
    """
        This function calculates the number of ways to make change for a given amount using a list of coins.
        In:
            * amount: The amount for which change is to be made.
            * coins:  The list of coins available to make change.
        Out:
            * The number of ways to make change for the given amount.
    """

    # Base cases
    if amount == 0:
        return 1
    if amount < 0 or len(coins) == 0:
        return 0
    
    # Recursive calls
    with_first_coin = count_coin_changes(amount - coins[0], coins)
    without_it = count_coin_changes(amount, coins[1:])
    return with_first_coin + without_it



print(count_coin_changes(4, [1, 2, 3]))  # 4
print(count_coin_changes(10, [2, 5, 3, 6]))  # 5
print(count_coin_changes(3, [2, 5]))  # 0

2.2 — Retour au problème du rendu de monnaie

Implémenter une définition récursive du problème du rendu de monnaie est basé sur la même idée que dans le problème du change de monnaie : nous choisissons une pièce et nous l’utilisons ou non. Nous pourrions décider, comme dans le problème du change de monnaie, d’utiliser la première pièce mais nous allons plutôt utiliser la dernière. Nous verrons pourquoi plus tard.

def change_making (amount, coins) -> int:
    
    """
        This function calculates the minimum number of coins needed to make change for a given amount.
        In:
            * amount: The amount for which change is to be made.
            * coins:  The list of coins available to make change.
        Out:
            * The minimum number of coins needed to make change for the given amount.
    """

    # Inner function to initialize utilitary parameters
    def __change_making (current_amount, i) -> int:
        
        """
            This helper function calculates recursively the minimum number of coins needed to make change for a given amount.
            In:
                * current_amount: The amount for which change is to be made.
                * i:              The index of the coin to be used.
            Out:
                * The minimum number of coins needed to make change for the given amount.
        """

        # Base cases
        if current_amount == 0:
            return 0
        if i == -1 or current_amount < 0:
            return float('inf')

        # There is the choice of using the ith coin or not
        return min(__change_making(current_amount, i - 1), 1 + __change_making(current_amount - coins[i], i))
    
    # Start with the coin of highest denomination
    return __change_making(amount, len(coins) - 1)



# Test cases
euros = [1, 2, 5, 10, 50]
assert(change_making(49, euros) == 7)  # [0, 2, 1, 4, 0]
assert(change_making(99, euros) == 8)  # [0, 2, 1, 4, 1]
print(change_making(99, euros))
print(change_making(49, euros))
old_pounds = [1, 3, 6, 12, 24, 30]
# 49 = 1 + 2 * 24
assert(change_making(49, old_pounds) == 3)  # [1, 0, 0, 0, 2, 0]
print(change_making(49, old_pounds))
foo = [2, 5]
assert(change_making(3, foo) == float('inf'))
print(change_making(3, foo))
print('All test cases passed!')

Il est simple d’implémenter une version mémoïsée du problème, en utilisant soit un dictionnaire soit un tableau bidimensionnel. Ceci est laissé comme exercice au lecteur. Tournons-nous maintenant vers la programmation dynamique.

2.3 — Une version de programmation dynamique du problème du rendu de monnaie

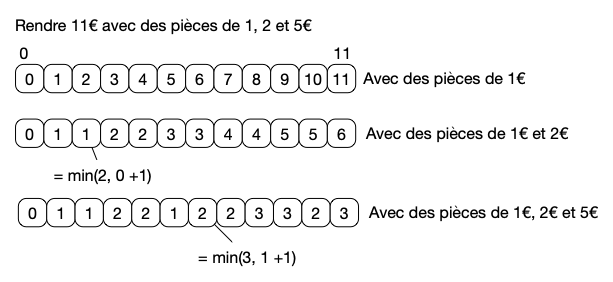
Implémenter la version de programmation dynamique du rendu de monnaie est basée sur l’idée que le nombre minimum de pièces nécessaires pour rendre un montant donné peut être calculé en considérant le nombre minimum de pièces nécessaires pour rendre des montants plus petits. Le graphe du problème est une chaîne, où chaque sommet correspond à un montant donné et les arêtes correspondent au choix d’utiliser une pièce ou non.

L’image ci-dessous illustre l’algorithme et sa stratégie de programmation dynamique s’appuyant sur la construction d’un tableau. Ici, chaque case du tableau indique le nombre minimum de pièces nécessaires pour obtenir la valeur correspondant à l’indice de la case dans le tableau.

def change_making_dp (amount, coins) -> int:
    
    """
        This function calculates, using dynamic programming, the minimum number of coins needed to make change for a given amount.
        In:
            * amount: The amount for which change is to be made.
            * coins:  The list of coins available to make change.
        Out:
            * The minimum number of coins needed to make change for the given amount.
    """

    # Initialize the table with infinity for all values except the first column
    table = [float('inf')] * (amount + 1)
    table[0] = 0

    # For each amount greater than or equal to the coin value
    for coin in coins:
        for i in range(coin, amount + 1):
            
            # check if using the current coin gives a better solution 
			# i.e., less coins for the amount - coin + 1
            table[i] = min(table[i], table[i - coin] + 1)

    return table[amount] if table[amount] != float('inf') else -1



# Test the function
print(change_making_dp(11, [1, 2, 5]))
print(change_making_dp(11, [1, 3, 4]))
print(change_making_dp(11, [1, 5, 6]))
print(change_making_dp(11, [1, 2, 5, 10]))

3 — Algorithmes gloutons

Les algorithmes gloutons font des choix au lieu de considérer toutes les possibilités. Ils élaguent la recherche en prenant de bonnes décisions locales, calculant un optimum local avec le risque de manquer l’optimum global. Considérons le problème du rendu de monnaie. Dans les versions précédentes, nous avons systématiquement considéré le choix d’utiliser ou non la pièce avec la plus haute dénomination. Une stratégie gloutonne consiste à choisir la pièce avec la plus haute dénomination tant que c’est possible. L’intuition est que, localement, cela semble plus efficace que de ne pas l’utiliser, en diminuant maximalement le montant à changer avec une seule pièce. En conséquence, l’algorithme peut cependant ignorer de meilleures solutions qui auraient été obtenues en considérant de ne pas l’utiliser.

La partie déroutante est que la version gloutonne du problème du rendu de monnaie fournit des solutions optimales avec certains systèmes monétaires, elle est alors extrêmement efficace même par rapport à la programmation dynamique, mais ignore les solutions optimales avec d’autres (c’est-à-dire qu’elle est tout simplement incorrecte). Voir le programme ci-dessous.

Quand on vise l’efficacité, un risque général est de :

• Utiliser une stratégie de programmation dynamique quand une stratégie gloutonne suffit.
• Utiliser une stratégie gloutonne quand une stratégie de programmation dynamique est requise (la stratégie gloutonne manque les solutions optimales).

Malheureusement, alors qu’il est assez facile de montrer qu’un algorithme glouton ne fonctionne pas, en trouvant un contre-exemple, il n’est pas si facile de montrer qu’il n’y a pas de contre-exemple.

Cela nécessite d’être très prudent et idéalement de faire des preuves, qu’un problème présente une sous-structure optimale, qu’une stratégie gloutonne retourne des solutions optimales.

3.1 — Une version gloutonne du problème du rendu de monnaie

def greedy_change (amount, coins) -> list[int]:

    """
        This function calculates the minimum number of coins needed to make change for a given amount using a greedy strategy.
        In:
            * amount: The amount for which change is to be made.
            * coins:  The list of coins available to make change, ordered in increasing order.
        Out:
            * A list of coin numbers i_1, i_2, ..., i_n such that i_1 * c_1 + i_2 * c_2 + ... = v.
    """

    # For each coin from the highest to the lowest
    solution = []
    for coin in reversed(coins):

        # Function divmod returns a tuple with the quotient and the remainder
        count, amount = divmod(amount, coin)
        solution.append(count)

    #Reverse the solution to have the coins in the same order as the input
    return solution[::-1]
	

	
# Test cases
euros = [1, 2, 5, 10, 50]
print(greedy_change(49, euros))  # [0, 2, 1, 4, 0]
print(greedy_change(99, euros))  # [0, 2, 1, 4, 1]
# The greedy algorithm does not always give the optimal solution
old_pounds = [1, 3, 6, 12, 24, 30]
# 49 = 1 + 6 + 12 + 30 = 1 + 2 * 24
print(greedy_change(49, old_pounds))  # [1, 0, 1, 1, 0, 1]

Pour aller plus loin

Il semble que cette section soit vide !

Y a-t-il des choses que vous auriez aimé voir ici ? Faites-le nous savoir sur le serveur Discord ! Peut-être pouvons-nous l’ajouter rapidement. Sinon, cela nous aidera à améliorer le cours pour l’année prochaine !

Pour aller au-delà

Il semble que cette section soit vide !

Y a-t-il des choses que vous auriez aimé voir ici ? Faites-le nous savoir sur le serveur Discord ! Peut-être pouvons-nous l’ajouter rapidement. Sinon, cela nous aidera à améliorer le cours pour l’année prochaine !