Activité pratique
Durée2h30Consignes globales
Dans cette activité, vous allez coder les algorithmes des K plus proches voisins (K-Nearest Neighbors, KNN) et des K moyennes (K-Means). La particulier de ces algorithmes, s’agissant d’apprentissage automatique, est qu’ils nécessitent une phase d’entraînement avant de pouvoir être utilisés pendant une phase de prédiction.
Nous vous proposons de coder ces algorithmes avec des classes en Python, en utilisant :
- la bibliothèque numpy pour les opérations sur les vecteurs et les matrices.
- une classe par algorithme, implémentant des méthodes pour la phase d’entraînement et la phase de prédiction.
- des tests unitaires pour vérifier le bon fonctionnement de vos implémentations.
Avant de commencer cette activité, assurez-vous d’avoir bien étudié l’article sur la manipulation des vecteurs et des matrices de la rubrique “Avant le cours” de cette séance !!
Contenu de l’activité
0 — Génération de données synthétiques
Avant de commencer à implémenter les algorithmes, il est utile de générer des données synthétiques pour tester vos implémentations. Utilisez la bibliothèque numpy pour créer des ensembles de données simples, comme expliqué dans l’activité préparatoire sur la manipulation des vecteurs et des matrices de la rubrique “Avant le cours” de cette séance.
Dans toute cette séance, nous allons utiliser des données en 2D pour faciliter la visualisation. Pour cette première étape, vous devez coder une fonction make_clouds qui génère des données synthétiques sous forme de nuages de points.
Coder une fonction make_clouds(num_clouds, points_per_cloud, cloud_centers, cloud_std) qui génère des données synthétiques.
Voici ses paramètres :
num_clouds: nombre de nuages de points à générerpoints_per_cloud: nombre de points par nuagecloud_centers: une liste de coordonnées pour les centres des nuages. Si ce n’est pas fourni, les centres doivent être générés aléatoirement dans un espace 2D.cloud_std: écart type des points autour de chaque centre de nuage
Cette fonction doit retourner un tableau Numpy X de forme (num_clouds * points_per_cloud, 2) contenant les points générés, ainsi qu’un tableau des étiquettes y de forme (num_cloud * points_per_cloud,) indiquant par un entier le cluster auquel chaque point appartient.
Visualisez les données générées avec la fonction scatter de matplotlib.pyplot pour vérifier que la fonction fonctionne correctement.
import matplotlib.pyplot as plt
X, y = make_clouds(num_clouds=3, points_per_cloud=100)
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()Ce code permet de visualiser les points avec des couleurs différentes selon leurs étiquettes. Vous devriez obtenir une visualisation similaire à celle-ci :
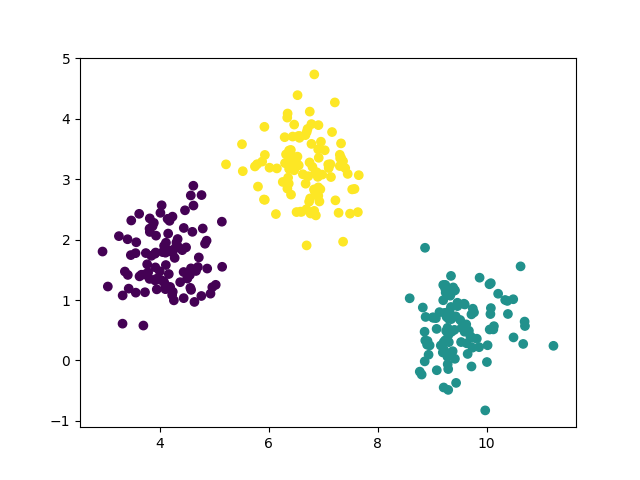
Testez de changer les paramètres de génération des données pour voir comment cela affecte la distribution des points. Cela vous aidera à comprendre les défis auxquels les algorithmes KNN et K-Means peuvent être confrontés.
1 — Les K plus proches voisins (K Nearest Neighbors, KNN)
1.1 — Algorithme
L’algorithme des KNN est un algorithme d’apprentissage supervisé qui fonctionne de la manière suivante :
- Lors de la phase d’entraînement, l’algorithme stocke les données d’entraînement.
- Lors de la phase de prédiction, pour chaque point de données à classer :
- Il calcule la distance euclidienne entre ce point et tous les points d’entraînement.
- Il identifie les K points d’entraînement les plus proches (les K plus proches voisins).
- Il attribue la classe la plus fréquente parmi ces K voisins au point de données.
1.2 — Implémentation
Identifiez les méthodes nécessaires pour implémenter l’algorithme des KNN dans une classe KNN, et créer le squelette de cette classe dans un fichier knn.py.
En particulier, l’initialisation de la classe KNN doit permettre de définir le paramètre K (nombre de voisins à considérer). A l’initialisation, préparez les attributs nécessaires pour stocker les données et étiquettes du jeux de données d’entraînement. Pour les méthodes, utilisez les noms train pour la phase d’entraînement et predict pour la phase de prédiction.
Utilisez la bibliothèque numpy pour implémenter les méthodes de la classe KNN, et mettez dans un fichier knn.py.
1.3 — Tests unitaires
Écrivez des tests unitaires pour vérifier le bon fonctionnement de votre implémentation de la classe KNN.
Vous pouvez prévoir des tests unitaires pour vérifier que :
- La méthode
trainstocke correctement les données d’entraînement. - La méthode
predictretourne les étiquettes correctes pour des points de test simples. Vous pouvez tester des points proches des points d’entraînement, et vérifier que le modèle prédit la bonne classe. - La méthode
predictlève une erreur si elle est appelée avant que le modèle ne soit entraîné.
1.4 — Tests sur les données synthétiques
Nous allons maintenant appliquer la classe KNN sur les données synthétiques générées à l’étape 0, et visualisons les résultats.
Tout d’abord, utilisons la fonction de l’étape 0 pour générer les données synthétiques. Pour pouvoir entrainer un KNN et le tester, il nous faut diviser les données en un ensemble d’entraînement et un ensemble de test. Nous prenons 80% des données pour l’entraînement et 20% pour le test, et nous mélangeons les données avant de les diviser. Voici un exemple de code pour cette étape :
# Générer des données synthétiques
X, y = make_clouds(num_clouds=3, points_per_cloud=50)
# Permuter les données, en permutant les indices, calculés à partir de la taille du vecteur y
nbpoints = y.shape[0]
indperm = np.random.permutation(nbpoints)
X = X[indperm]
y = y[indperm]
# Diviser les données en ensembles d'entraînement et de test
split_index = int(0.8 * len(X))
X_train, X_test = X[:split_index], X[split_index:]
y_train, y_test = y[:split_index], y[split_index:]Ensuite, nous pouvons entraîner le modèle KNN sur l’ensemble d’entraînement, faire des prédictions sur l’ensemble de test, et calculer la précision des prédictions.
Utilisez les données synthétiques générées à l’étape 0 pour tester votre implémentation de la classe KNN :
- Entraînez le modèle sur l’ensemble d’entraînement
X_train,y_train, - faites des prédictions sur l’ensemble de test
X_test, - puis calculez la précision de vos prédictions, c’est à dire le pourcentage de prédictions correctes, estimées à partir de
y_test.
Afin de comprendre l’impact du choix de K sur les performances du modèle, essayez de modifier la valeur de K et observez comment cela affecte la précision. D’autre part, essayez de modifier les paramètres de génération des données pour voir comment cela affecte les résultats, par exemple en augmentant l’écart type des nuages ou en réduisant la distance entre les centres des nuages.
Nous vous conseillons de visualiser les résultats avec matplotlib en utilisant des symboles différents pour les données de test et d’entraînement. Voici un exemple de code visualisation (en supposant que les données d’entraînement sont dans X_train avec étiquettes y_train, les données de test dans X_test et les predictions contient les étiquettes prédites pour X_test) :
import matplotlib.pyplot as plt
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, marker='o', label='Données d\'entraînement')
plt.scatter(X_test[:, 0], X_test[:, 1], c=predictions, marker='x', label='Données de test (prédictions)')
plt.legend()
plt.show()Vous devriez obtenir une visualisation similaire à celle-ci :
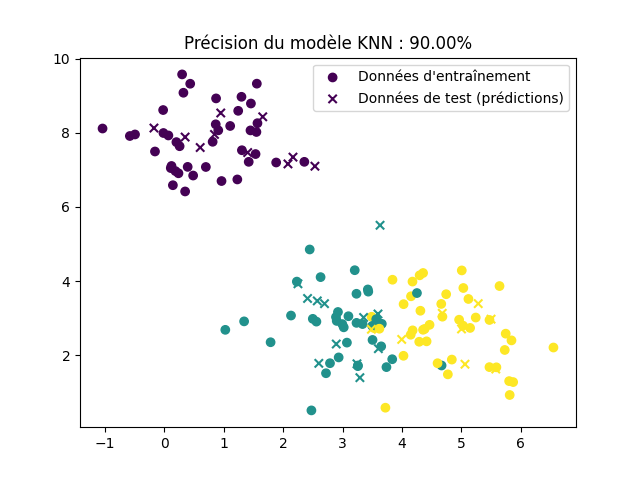
2 — Les K moyennes (K-Means)
2.1 — Algorithme
L’algorithme des K-Means est un algorithme d’apprentissage non supervisé qui fonctionne de la manière suivante :
- Initialisation : Choisir K centres de clusters initiaux (centroïdes) de manière aléatoire.
- Itération :
- Assignation : Pour chaque point de données, assigner le point au cluster dont le centroïde est le plus proche (en utilisant la distance euclidienne).
- Mise à jour : Recalculer les centroïdes en prenant la moyenne des points assignés à chaque cluster.
- Répéter les étapes d’assignation et de mise à jour jusqu’à convergence (c’est-à-dire jusqu’à ce que les centroïdes ne changent plus significativement).
Pour la convergence, on peut définir un critère d’arrêt basé sur un nombre maximum d’itérations ou sur une tolérance $\epsilon$ de changement des centroïdes.
2.2 — Implémentation
Identifiez les méthodes nécessaires pour implémenter l’algorithme des K-Means dans une classe KMeans, et créer le squelette de cette classe dans un fichier kmeans.py.
Il faut prévoir des attributs pour stocker les centroïdes, le nombre de clusters K, le nombre maximum d’itérations, et la tolérance pour la convergence. A noter en particulier qu’il sera utile de visualiser les centroïdes à l’issue de l’apprentisage. Vous pouvez donner le nom centroids à l’attribut stockant les centroïdes. Pour les méthodes, utilisez les noms train pour la phase d’entraînement et predict pour la phase de prédiction.
Utilisez la bibliothèque numpy pour implémenter les méthodes de la classe KMeans.
2.3 — Tests sur les données synthétiques
Pour finir, nous allons appliquer la classe KMeans sur les données synthétiques générées à l’étape 0, et visualiser les résultats.
Vous devriez obtenir une visualisation similaire à celle-ci :
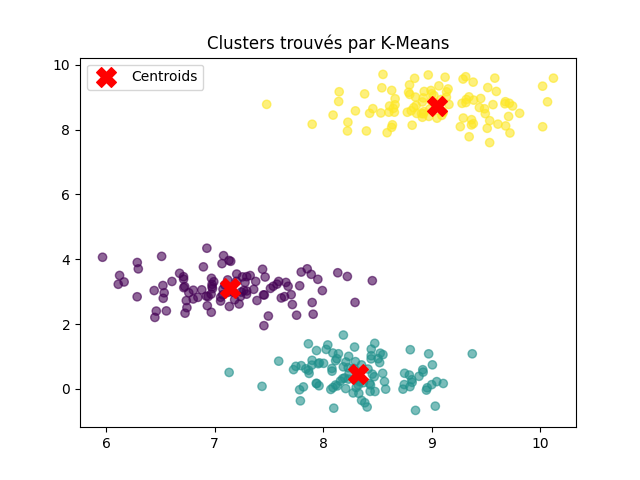
Utilisez les données synthétiques générées à l’étape 0 pour tester votre implémentation de la classe KMeans. Vous n’avez pas besoin des étiquettes réelles pour entraîner le modèle, car K-Means est un algorithme non supervisé.
Vous pouvez visualiser les clusters trouvés par l’algorithme en utilisant matplotlib.
Il est très facile d’obtenir un bon clustering avec K-Means sur des données synthétiques bien séparées. Essayez de modifier les paramètres de génération des données pour voir comment cela affecte les résultats, par exemple en augmentant l’écart type des clusters ou en réduisant la distance entre les centres des clusters.