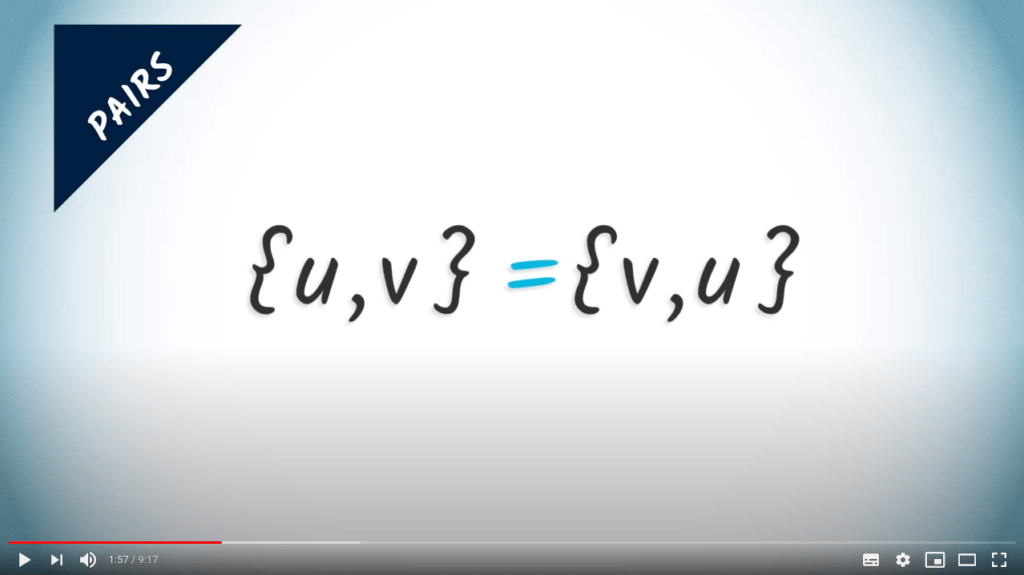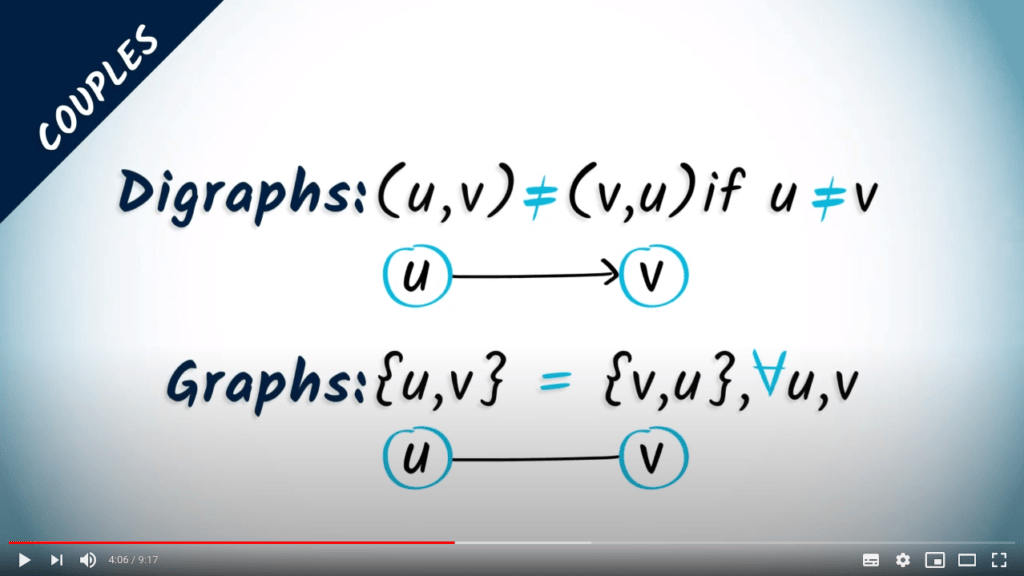Graphes & Chemins

Bonjour et bienvenue dans cette leçon ! Aujourd’hui, nous allons introduire quelques définitions de base liées aux graphes.

Définitions de base

La théorie des graphes est probablement l’un des sous-domaines les plus courants des mathématiques discrètes. Les graphes sont des structures mathématiques utilisées pour représenter les relations entre des objets.

Mathématiquement, un graphe est composé d’un ensemble fini de sommets, $V$, et d’un ensemble d’arêtes, $E$. Nous pouvons donc désigner un graphe comme un couple $G = (V, E)$ composé de $V$ et $E$.

Un graphe est souvent représenté par des cercles pour les sommets et des lignes pour les arêtes.

Quelques exemples : les graphes peuvent être utilisés pour représenter les relations entre les membres d'une famille dans un arbre généalogique, où les membres sont représentés comme des sommets et leurs relations comme des arêtes...

Ou, de manière similaire, pour représenter les interactions moléculaires dans un organisme biologique...

Ou, les réseaux neuronaux dans le cerveau...

Les hyperliens entre sites web...

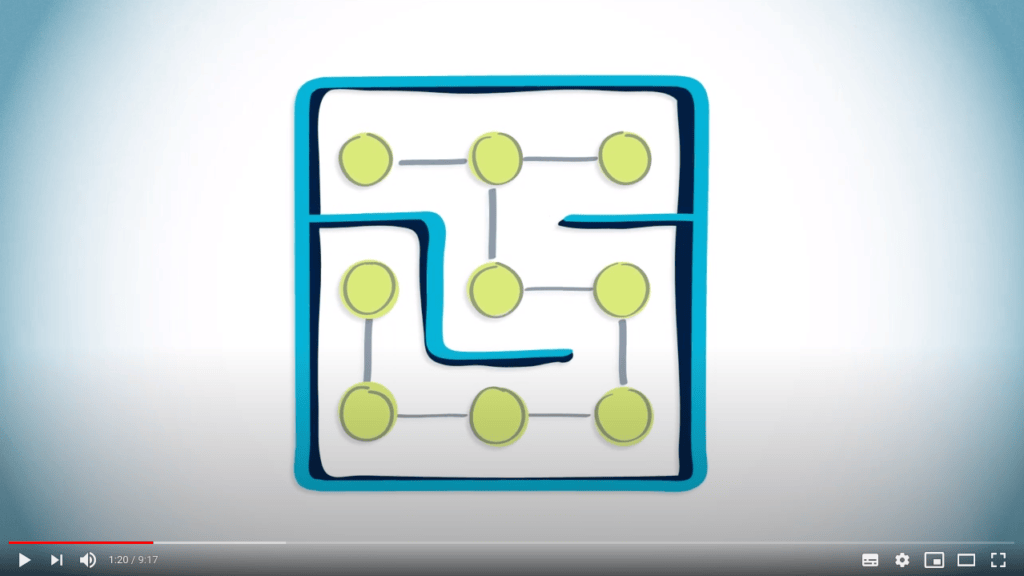
Ou, tout simplement, un labyrinthe, où les cellules peuvent être représentées comme des sommets, et les cellules adjacentes non séparées par un mur peuvent être reliées par des arêtes.

C’est exact. Il existe plusieurs façons de définir les graphes. Dans le cas le plus simple, les arêtes transmettent des informations sur les paires de sommets qui sont connectées et celles qui ne le sont pas. Cela signifie que $E$ devient un ensemble de paires de sommets.

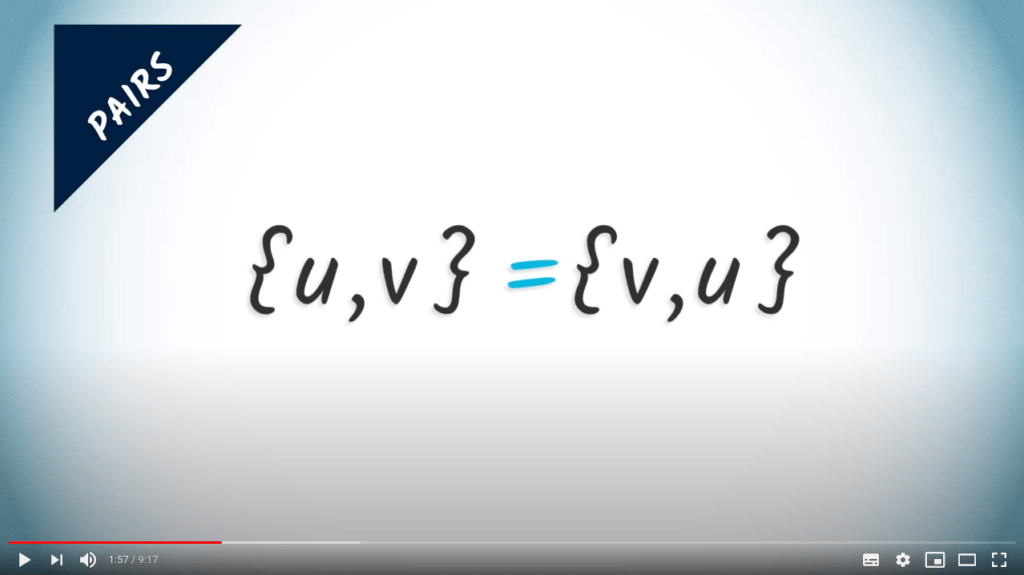
Une paire $\{u,v\}$ est un ensemble non ordonné contenant deux éléments distincts, $u$ et $v$. Étant donné qu'elles ne sont pas ordonnées, les paires $\{u,v\}$ et $\{v,u\}$ sont identiques.

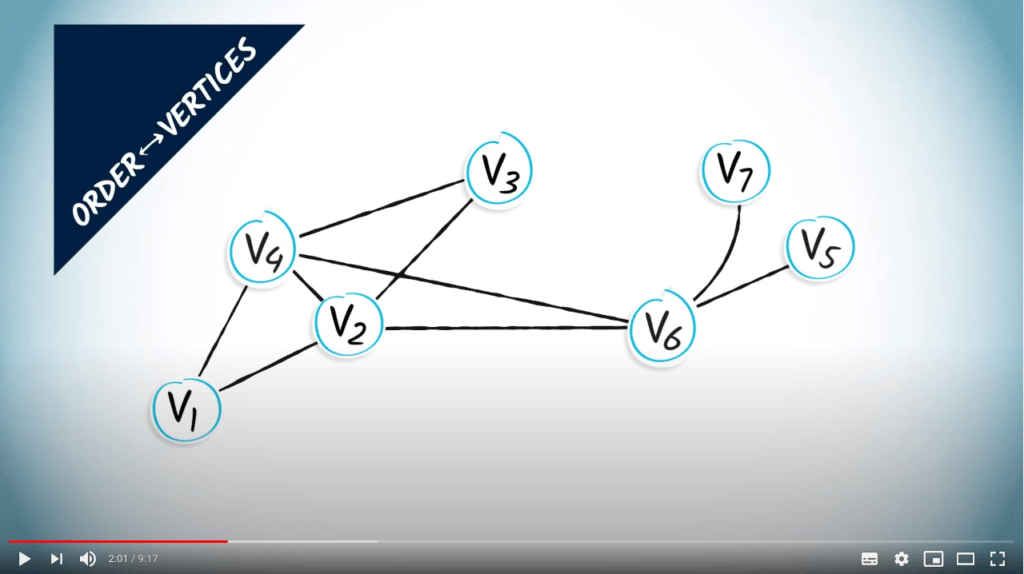
L'ordre d'un graphe est le nombre de sommets qu'il contient, qui est de 7 dans cet exemple.

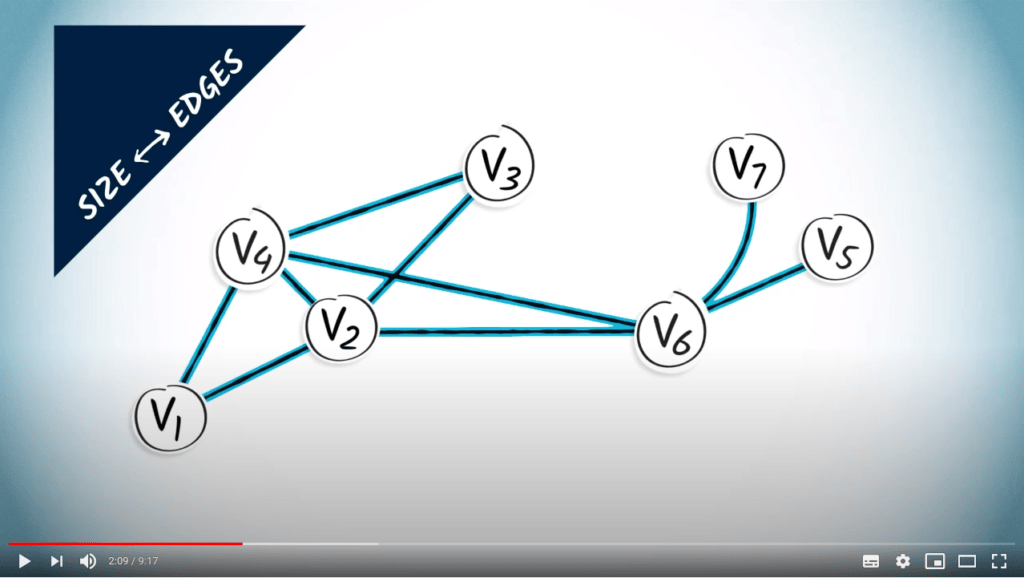
La taille du graphe est le nombre d'arêtes, qui est de 9 dans cet exemple.

Comme vous pouvez le voir, c’est une manière simple et efficace de visualiser un graphe.

Mais cela peut également être trompeur, car la création d’une figure comme celle-ci nécessite de prendre des décisions arbitraires sur les coordonnées des sommets et les formes des lignes.

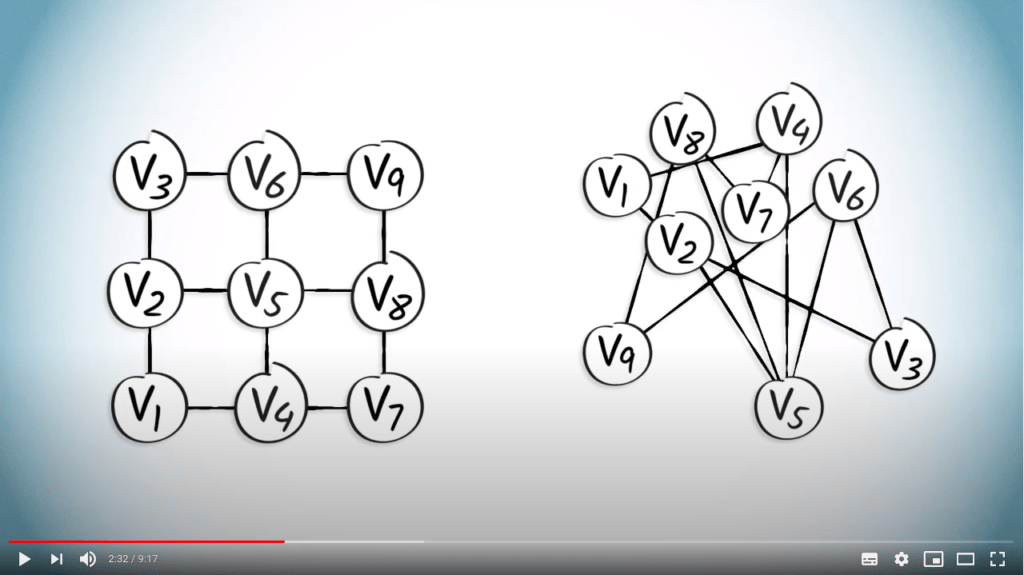
Cela peut être observé dans l'exemple suivant, qui montre deux graphes qui semblent différents. Cependant, ces deux graphes sont identiques dans le sens où ils ont exactement le même ensemble de sommets et le même ensemble d'arêtes.

Les graphes ont été introduits pour la première fois par Euler en 1736.

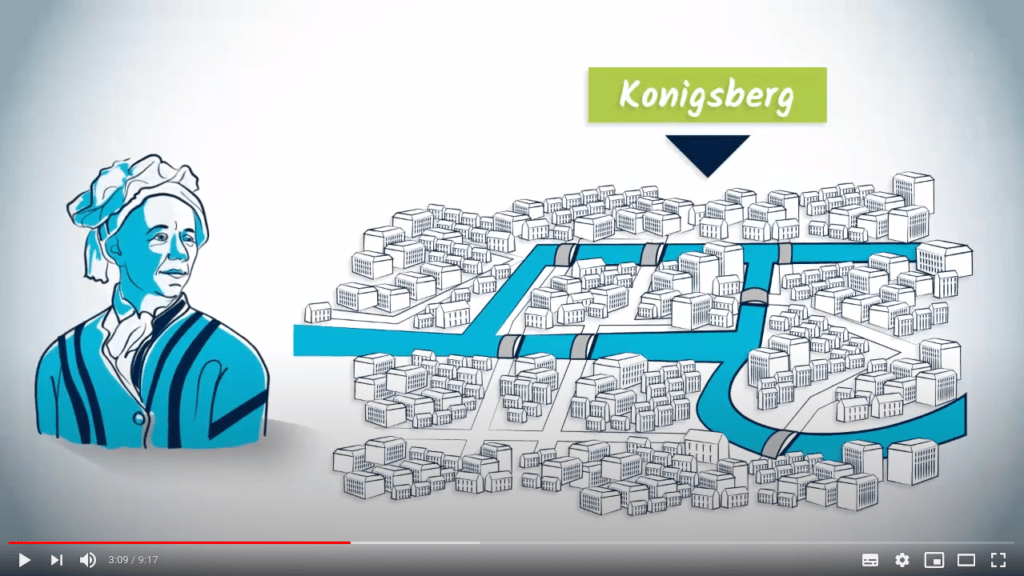
Il s'intéressait à prouver formellement qu'il était impossible de se promener dans la ville de Königsberg en traversant chacun de ses ponts exactement une fois. Pour le prouver, il a montré que commencer et finir à un même point nécessiterait que le graphe contienne 0 ou 2 masses terrestres avec un nombre impair de ponts. Étant donné que toutes les masses terrestres de Königsberg contenaient un nombre impair de ponts, cet itinéraire était impossible.

Dans certains cas, les arêtes peuvent être orientées, ce qui signifie qu’un sommet $u$ peut être connecté à un sommet $v$, même si $v$ n’est pas connecté à $u$. Dans de tels cas, les arêtes sont constituées de couples de sommets, tels que, par exemple, $(u,v)$.

Les couples sont plus informatifs que les paires car l’ordre des sommets dans le couple est significatif.

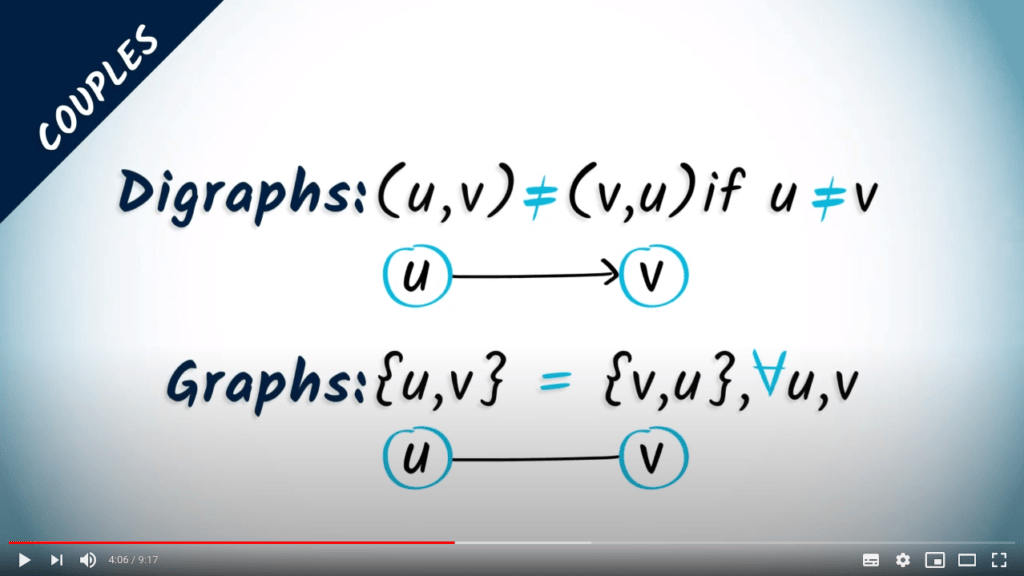
Par exemple, le couple $(u,v)$ est distinct du couple $(v,u)$ si $u$ et $v$ sont eux-mêmes distincts, tandis que la paire $\{u,v\}$ et la paire $\{v,u\}$ sont identiques. Lorsqu'on utilise des couples, les graphes sont appelés digraphes. Nous ne considérerons que des graphes dont les arêtes sont des paires dans ce cours, mais il est utile de noter que les algorithmes présentés ici s'appliquent également aux digraphes.

La matrice d'adjacence et les graphes pondérés

Comme dans les exemples précédents, il est préférable d'indexer les sommets de 1 à $n$, qui est l'ordre du graphe. Lorsque les sommets du graphe sont indexés de manière appropriée, une autre façon de représenter un graphe est d'utiliser une matrice.

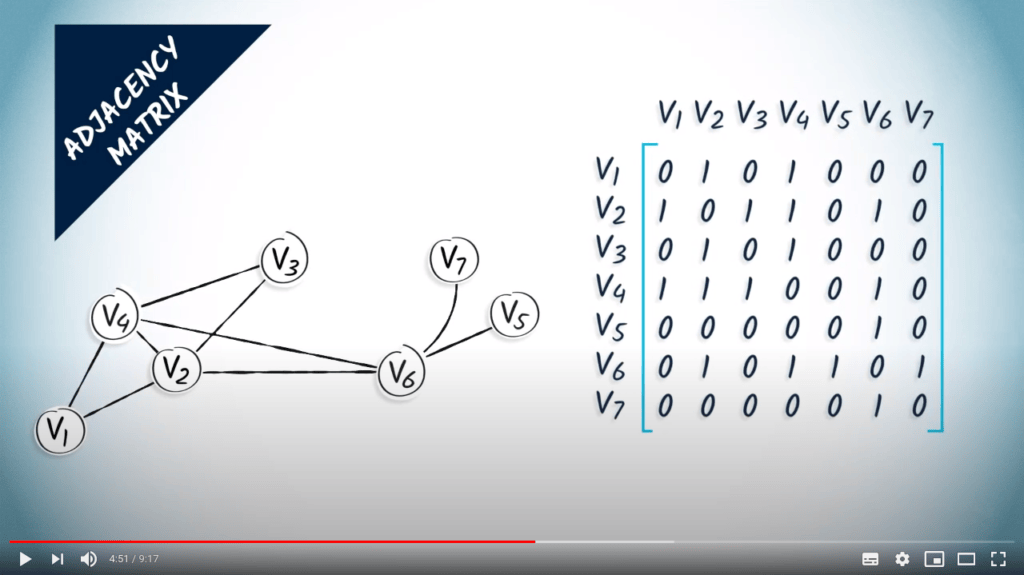
La matrice d'adjacence d'un graphe est une matrice ayant autant de lignes et de colonnes que l'ordre du graphe. La matrice d'adjacence est construite en mettant un 1 à la ligne $i$ et à la colonne $j$ si $\{i,j\}$ est une arête, et en mettant un 0 sinon. Voici un exemple d'un graphe et de sa matrice d'adjacence correspondante.

Vous devez noter que la matrice d’adjacence d’un graphe est toujours symétrique.

Les matrices d’adjacence peuvent être généralisées pour prendre des valeurs autres que 0 et 1, ce qui permet de définir des graphes pondérés.

Les graphes pondérés sont particulièrement utiles lorsque les arêtes représentent des distances ou des délais entre les sommets, car les valeurs dans la matrice d’adjacence peuvent être utilisées pour indiquer les quantités correspondantes.

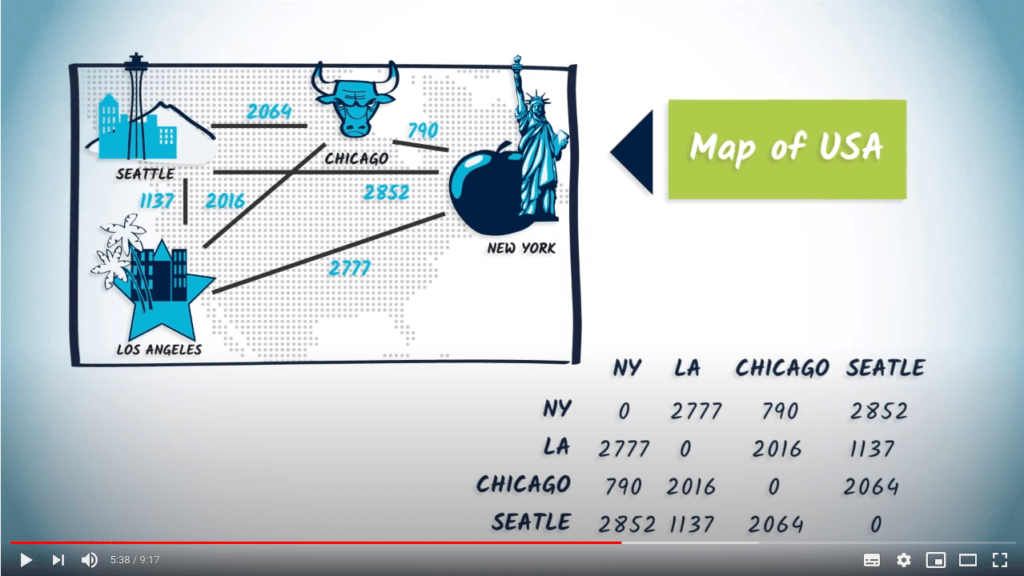
Pour prendre un exemple, un graphe pondéré peut modéliser les distances entre les grandes villes des États-Unis, et les poids des connexions peuvent être utilisés pour représenter ces distances. En plus des distances, les poids peuvent être utilisés pour représenter des occurrences, des proximités, des relations, et ainsi de suite.

Chemins et distances géodésiques

Un chemin est une séquence ordonnée d'arêtes distinctes les unes des autres, obtenue à partir d'une séquence de sommets en reliant deux sommets consécutifs par l'arête correspondante. Les deux sommets extrêmes de la séquence sont appelés les extrémités du chemin.

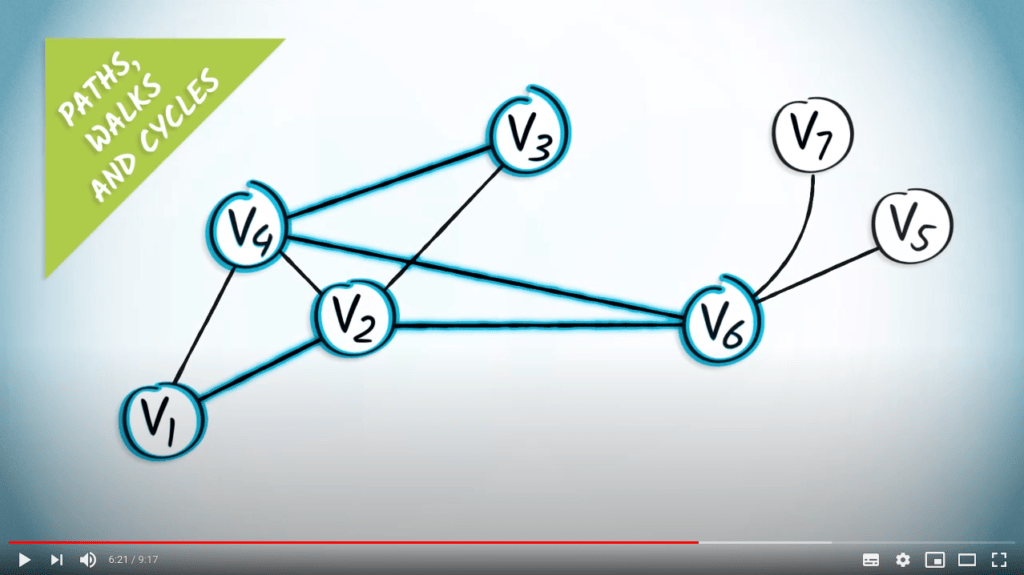
Regardez ce graphe. Dans cet exemple, $(\{v_1,v_2\}, \{v_2,v_6\}, \{v_4,v_6\}, \{v_3,v_4\})$ est un chemin, obtenu à partir de la séquence de sommets $(v_1,v_2,v_6,v_4,v_3)$.

Les chemins sont souvent confondus avec les marches. Une marche est une séquence de sommets, où chaque paire de sommets consécutifs forme une arête dans le graphe. La différence est que, dans un chemin, une arête ne peut pas apparaître deux fois.

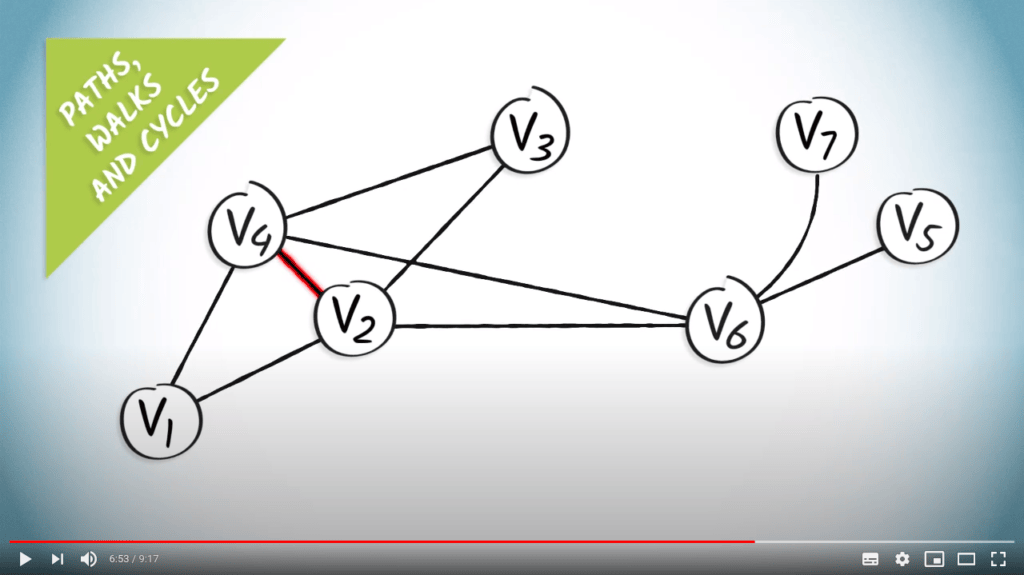
Par exemple, $(v_1, v_2, v_4, v_2)$ dans le graphe précédent est une marche, mais la séquence correspondante $(\{v_1,v_2\}, \{v_2, v_4\}, \{v_2,v_4\})$ n'est pas un chemin, en raison de la répétition de l'arête $\{v_2,v_4\}$.

Un cycle dans un graphe est un chemin dont les extrémités sont identiques.

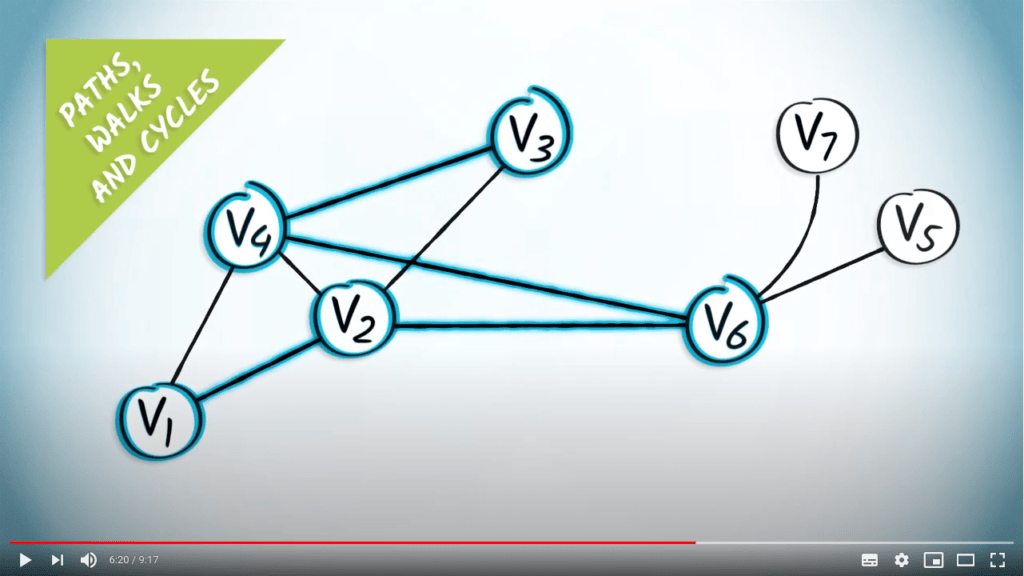
Par exemple, dans le graphe précédent, $(\{v_2,v_6\}, \{v_4,v_6\}, \{v_3,v_4\}, \{v_2,v_3\})$ est un cycle obtenu à partir de la séquence de sommets $(v_2, v_6, v_4, v_3, v_2)$.

La longueur d’un chemin est la longueur de la séquence d’arêtes. Pour les graphes pondérés, la longueur correspond à la somme des poids.

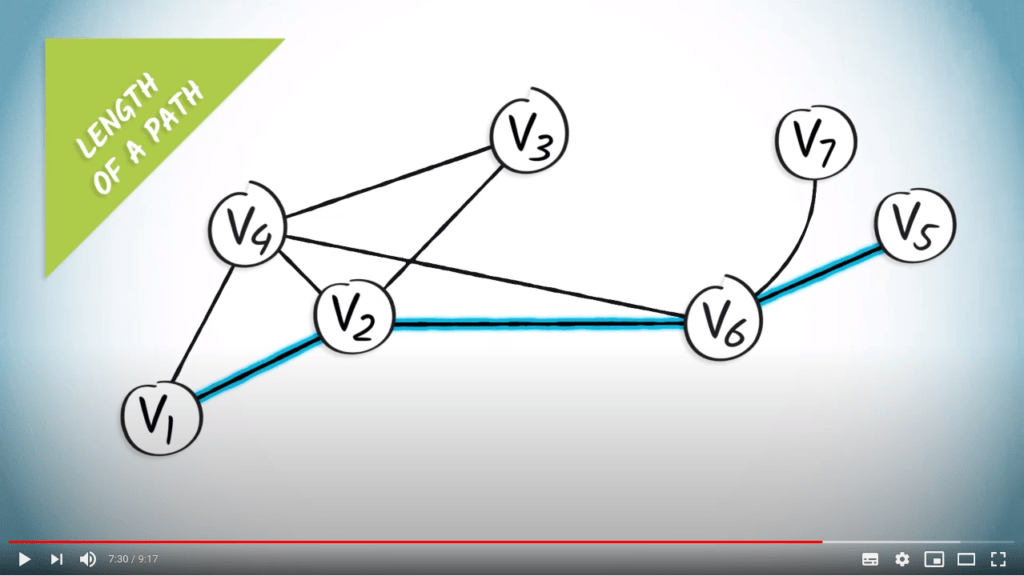
S'il existe au moins un chemin reliant deux sommets $u$ et $v$, il existe un chemin le plus court. La plupart des leçons suivantes seront consacrées à apprendre comment trouver les chemins les plus courts entre deux sommets dans un graphe.

Enfin, un graphe est dit connexe si, pour tous les couples de sommets, il existe un chemin ayant ces sommets comme extrémités.

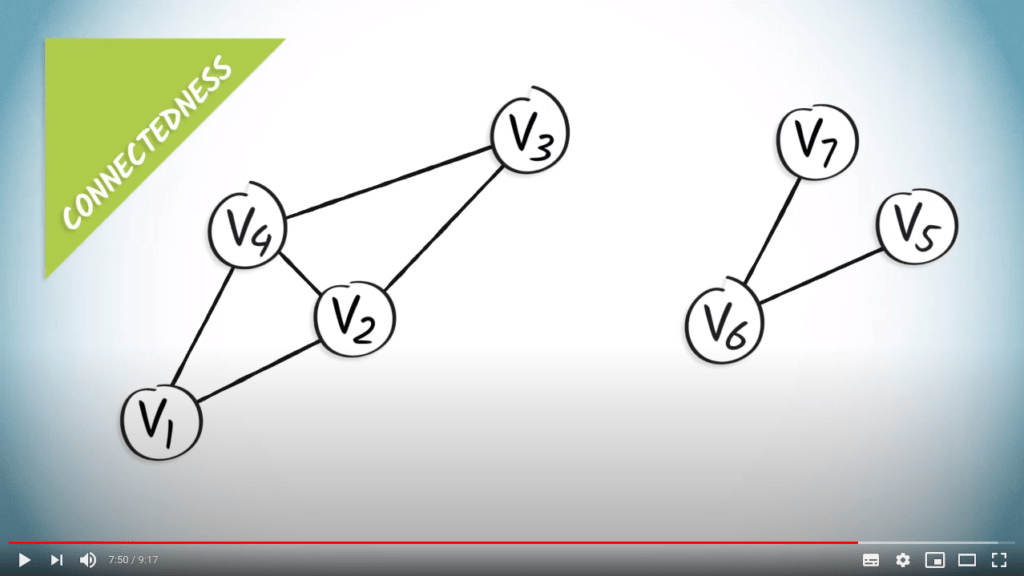
Tous les graphes d'exemple que nous avons considérés jusqu'à présent sont connexes. Voici un graphe qui n'est pas connexe.

Graphes standards

Certains graphes sont très utiles car ils peuvent apparaître dans de nombreuses situations.

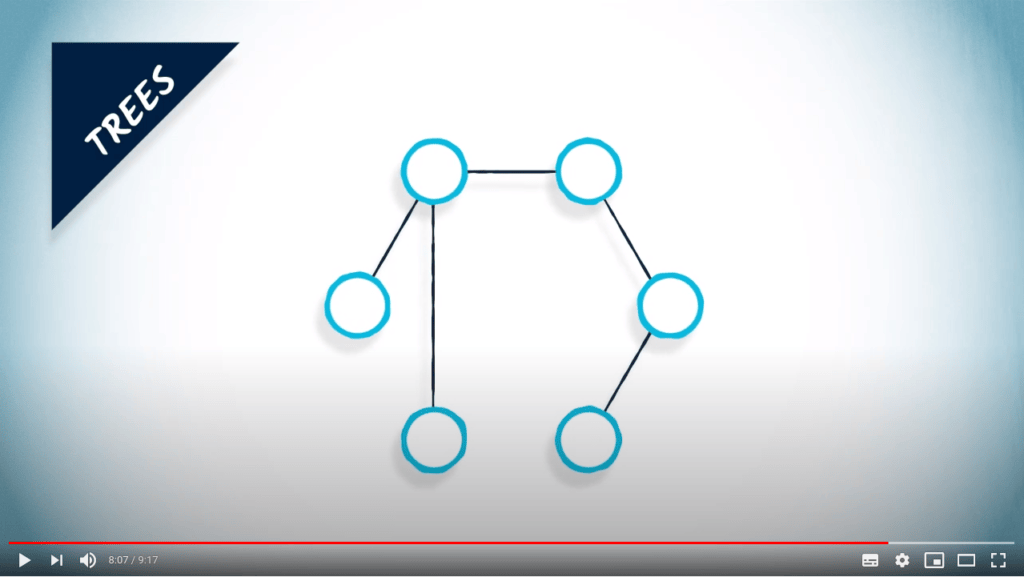
Par exemple, nous rencontrons des arbres tout le temps : dans les systèmes de fichiers, dans les graphes généalogiques, dans les compétitions sportives où les tournois sont souvent représentés sous forme d'arbres, et ainsi de suite.

Les arbres sont des graphes connexes sans cycles.

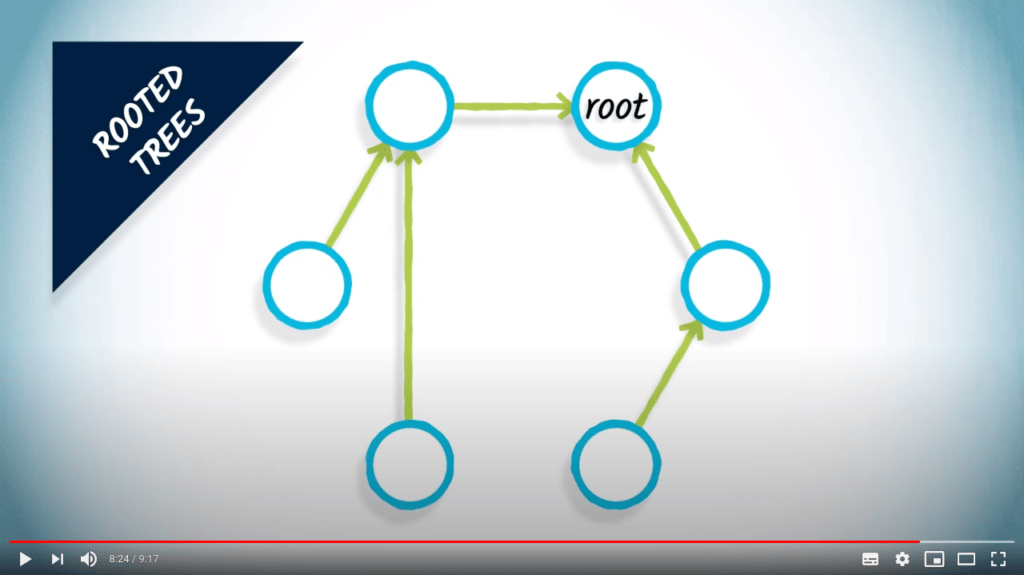
Notez que les arbres sont souvent confondus avec les arbres enracinés, dans lesquels les sommets connectés ont une relation spécifique les uns avec les autres. Les arbres enracinés peuvent être définis en choisissant un sommet arbitraire comme racine de l'arbre.

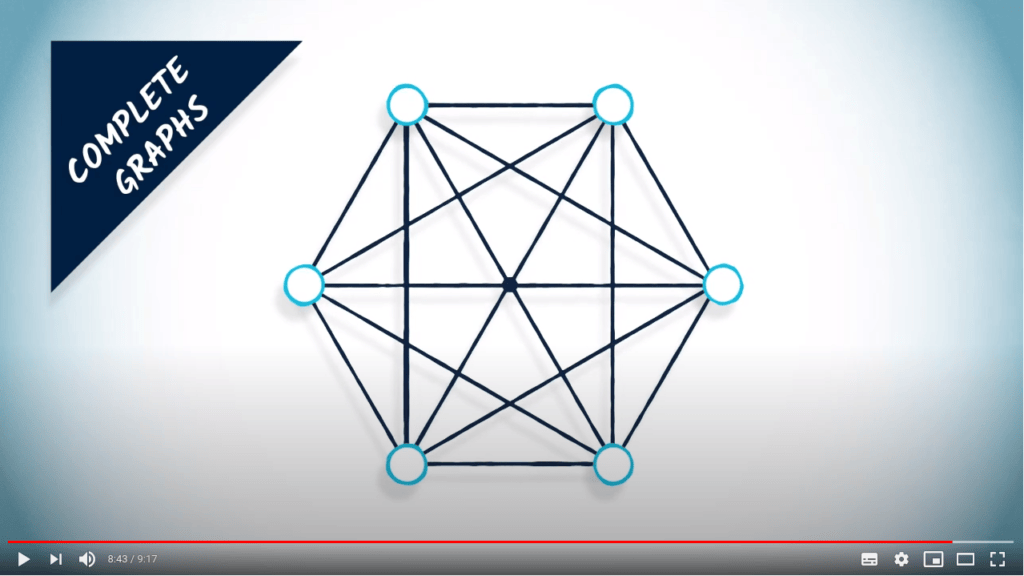
Un autre exemple de graphe standard est le graphe complet. Un graphe complet inclut toutes les arêtes possibles, et est souvent un bon choix pour tester les capacités ou le temps de calcul d'un algorithme opérant sur des graphes.

Les labyrinthes peuvent également être représentés sous forme de graphes. Dans ce cas, les sommets peuvent représenter les cellules du labyrinthe, et les arêtes peuvent être définies comme les cellules voisines qui ne sont pas séparées par un mur.

Conclusion

Merci pour votre attention ! J’ai vraiment apprécié parler de théorie des graphes avec vous aujourd’hui.