Representer les graphes
Temps de lecture5 minEn bref
Résumé de l’article
Dans cet article, vous découvrirez des solutions pour représenter des graphes en mémoire dans un ordinateur. Après la vidéo, nous vous présenterons la structure de graphe que vous manipulerez dans le projet PyRat.
À retenir
-
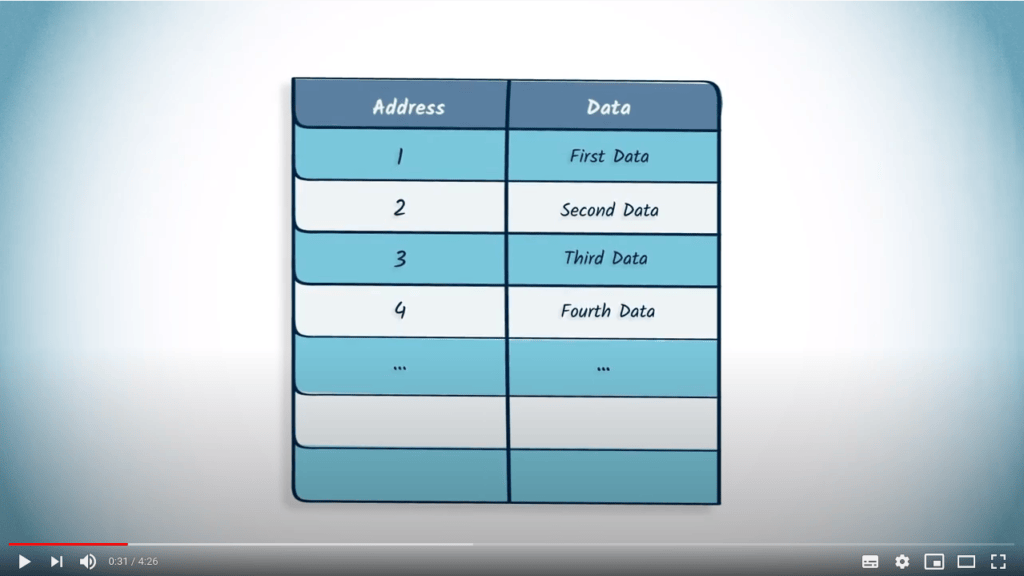
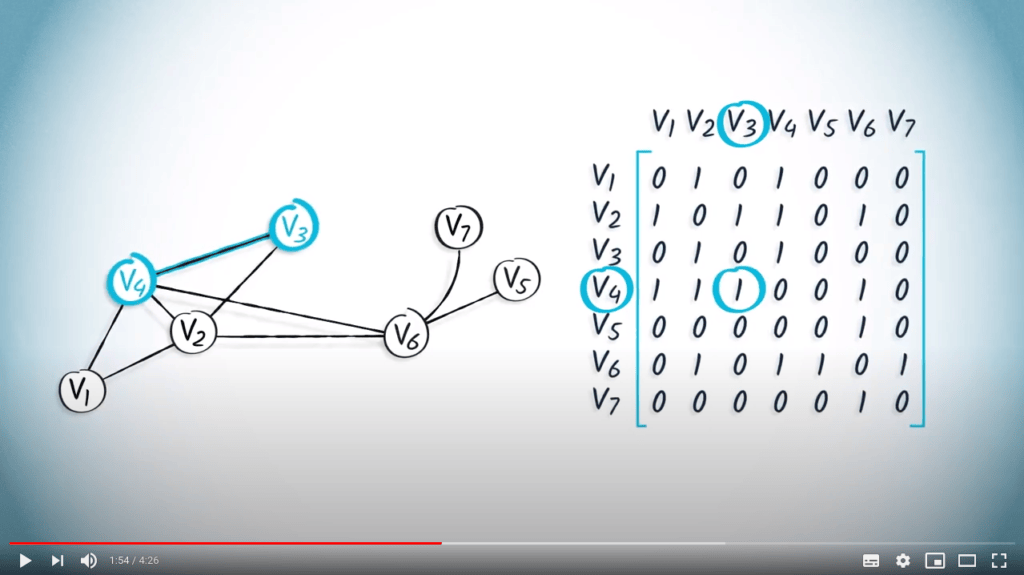
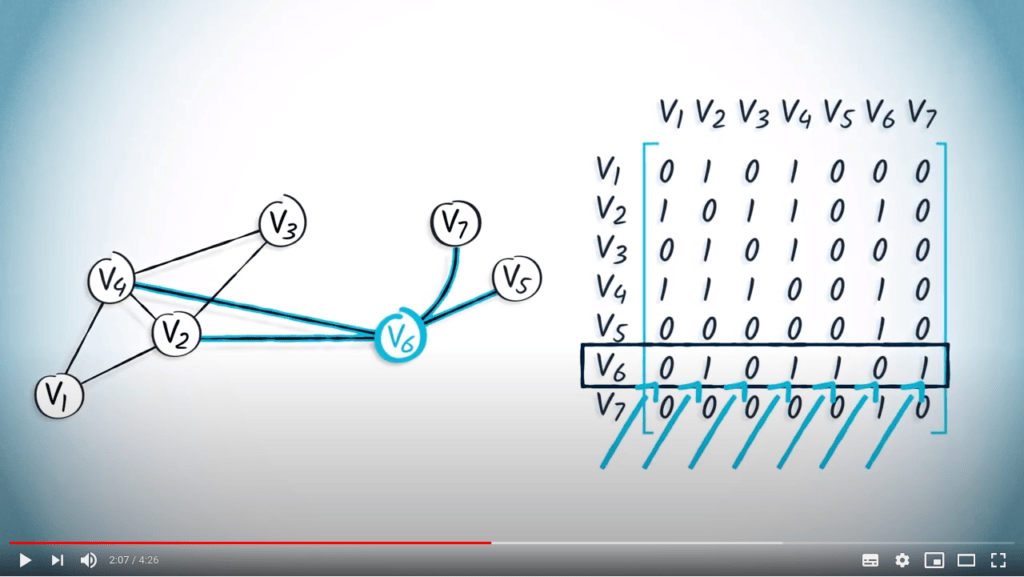
La matrice d’adjacence d’un graphe peut être représentée en mémoire à l’aide d’un tableau.
-
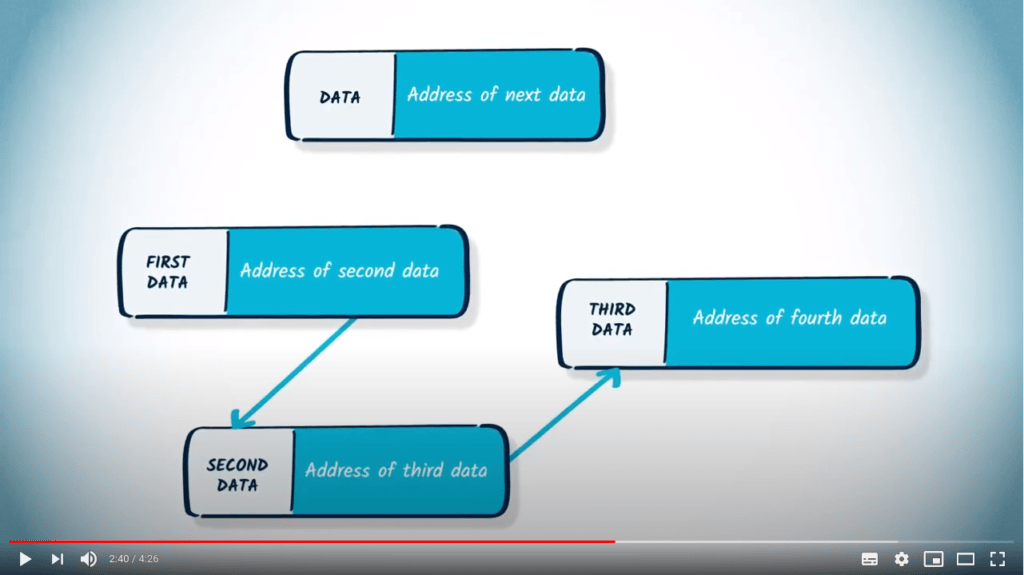
Les listes et les dictionnaires sont également des solutions pour représenter un graphe en mémoire.
-
Chaque représentation a ses propres avantages et inconvénients.
-
Dans PyRat, la représentation d’un graphe est abstraite dans un objet.
Contenu de l’article
1 — Vidéo
Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.
2 — La représentation d’un graphe dans PyRat
Dans le logiciel PyRat, le graphe est encapsulé dans un objet, i.e., une structure complexe qui vous fournit une interface pratique pour le manipuler. En d’autres termes, vous n’avez pas un accès direct à la matrice d’adjacence, à la liste ou au dictionnaire qui stocke le graphe en mémoire. À la place, vous avez accès à de nombreux attributs et méthodes qui vous permettent de manipuler le graphe sans entrer dans les détails de son implémentation.
Plus précisément, soit g une instance de la classe Graph de PyRat.
Vous pouvez utiliser les fonctions décrites dans la documentation de la classe Game.
En pratique, un labyrinthe PyRat est une instance de la classe Maze, qui hérite de Graph.
Ainsi, il possède quelques attributs supplémentaires (e.g., une width et une height en nombre de cases) et des méthodes supplémentaires (e.g., coords_difference(v1, v2) pour obtenir la différence selon les axes de largeur et de hauteur, i_exists(v) pour vérifier qu’une case existe dans le labyrinthe).
Consultez la documentation de la classe Maze pour plus d’informations !
Vous voyez, à aucun moment vous n’avez besoin de connaître la structure sous-jacente pour utiliser le graphe dans votre projet. C’est très pratique si le développeur de PyRat décide un jour de modifier cette structure pour une raison quelconque. En effet, tant que l’interface reste inchangée, le code des utilisateurs continuera de fonctionner.
Il existe de nombreuses bibliothèques en ligne qui fournissent de telles interfaces pour utiliser des graphes. Quel que soit le langage que vous utilisez, il est toujours judicieux de vérifier les implémentations existantes avant de réimplémenter une structure à partir de zéro !
Pour aller plus loin
3 — Plus de détails sur la solution basée sur les listes
Nous avons vu précédemment qu’une matrice d’adjacence est un objet pratique pour représenter un graphe en mémoire.
Cependant, dans la plupart des cas, les graphes sont des objets creux, i.e., le nombre d’arêtes existantes est faible par rapport au nombre d’arêtes d’un graphe complet. Une conséquence directe est que la plupart des entrées de la matrice d’adjacence sont des 0. Étant donné que le nombre d’éléments dans une matrice d’adjacence est égal au carré de l’ordre du graphe, cela peut rapidement entraîner une utilisation importante de l’espace mémoire.
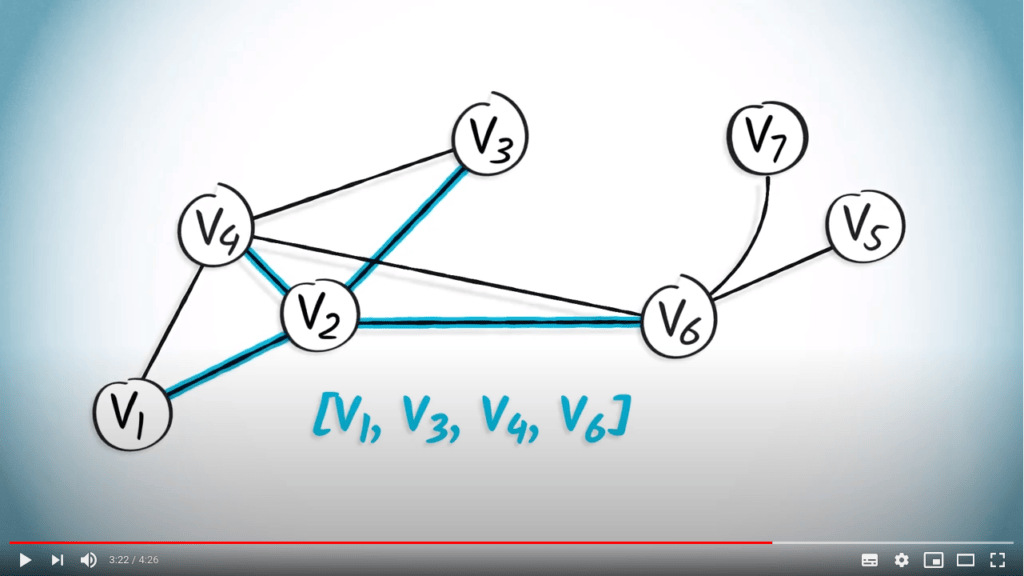
Une solution possible pour contourner ce problème est d’utiliser une structure de données différente : une liste de listes. Appelons un tel objet $L = (l_1, \dots, l_n)$, avec $l_1, \dots, l_n$ étant des listes. Dans cette structure, $l_i$ $(i \in [1, n])$ représentera les arêtes accessibles depuis le sommet $i$.
À titre d’exemple, considérons la matrice d’adjacence suivante : $${\bf A} = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{pmatrix}$$
En supposant que les sommets soient étiquetés de 1 à $n$, cette matrice est équivalente à la liste $L = ( (2, 4) , (1, 3, 4, 6), (2, 4), (1, 2, 3, 6), (6), (2, 4, 5, 7), (6) )$.
On peut rapidement remarquer que le nombre de nombres stockés est passé de $n^2$ = 49 à 18.
Bien que cette solution permette d’économiser de l’espace mémoire, elle présente certaines limitations :
-
Vérifier l’existence d’une arête ${i, j}$ nécessite de parcourir tous les éléments de la liste $l_i$ pour vérifier si $j$ en fait partie. Cela peut prendre du temps si $i$ a de nombreux voisins. En comparaison, effectuer la même vérification avec une matrice d’adjacence ${\bf A}$ ne nécessite qu’une seule opération, car il suffit de vérifier que ${\bf A}[i, j] \neq 0$.
-
Elle est moins facile à étendre aux graphes pondérés. Dans le cas des matrices d’adjacence, les entrées représentent le poids associé à l’arête. Ici, les entrées sont les indices des éléments non nuls, qui ne peuvent pas être modifiés sans créer ou supprimer des arêtes. Une solution possible consiste à remplacer les listes d’indices $l_i = (j, k, \dots)$ par des listes de couples $l_i = ( (j, w_j), (k, w_k), \dots )$, où $w_j$ est le poids de l’arête ${i, j}$.
Pour aller encore plus loin
-
Understanding the Efficiency of GPU Algorithms for Matrix-Matrix Multiplication.
Un article de recherche illustrant l’une des principales raisons pour lesquelles les matrices sont fréquemment utilisées.
-
Graph Processing on FPGAs: Taxonomy, Survey, Challenges.
Un article de recherche illustrant l’utilisation de matériel spécifique (ici, FPGA) pour traiter de grands graphes.