Algorithme de Dijkstra

Temps de lecture20 min

En bref

Résumé de l’article

Dans cet article, vous apprendrez à naviguer dans un graphe pondéré. Vous verrez que les parcours vus précédemment ne peuvent pas être utilisés directement. C’est pourquoi nous introduisons un autre algorithme de parcours : l’algorithme de Dijkstra.

Points clés à retenir

  • L’algorithme de Dijkstra étend le BFS pour effectuer un parcours sur des graphes pondérés.

  • Il trouve un chemin le plus court entre un sommet source et les autres sommets atteignables dans des graphes pondérés positivement.

  • Avec un tas min binaire comme heapq, il a une complexité de $O((|V| + |E|) \cdot log(|V|))$.

Contenu de l’article

Vidéo

Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Information
Cliquez ici pour afficher la traduction de la vidéo.

Bonjour et bienvenue dans cette leçon sur l’algorithme de Dijkstra ! Cette semaine, nous allons parler des chemins les plus courts dans les graphes pondérés. Les algorithmes de parcours de graphe que nous avons déjà vus dans la leçon précédente ne peuvent pas être directement appliqués pour trouver les chemins les plus courts dans les graphes pondérés.

Graphe pondéré

Pour illustrer pourquoi les algorithmes de parcours de graphe déjà présentés ne fonctionnent pas nécessairement pour les graphes pondérés, considérons le graphe jouet suivant.

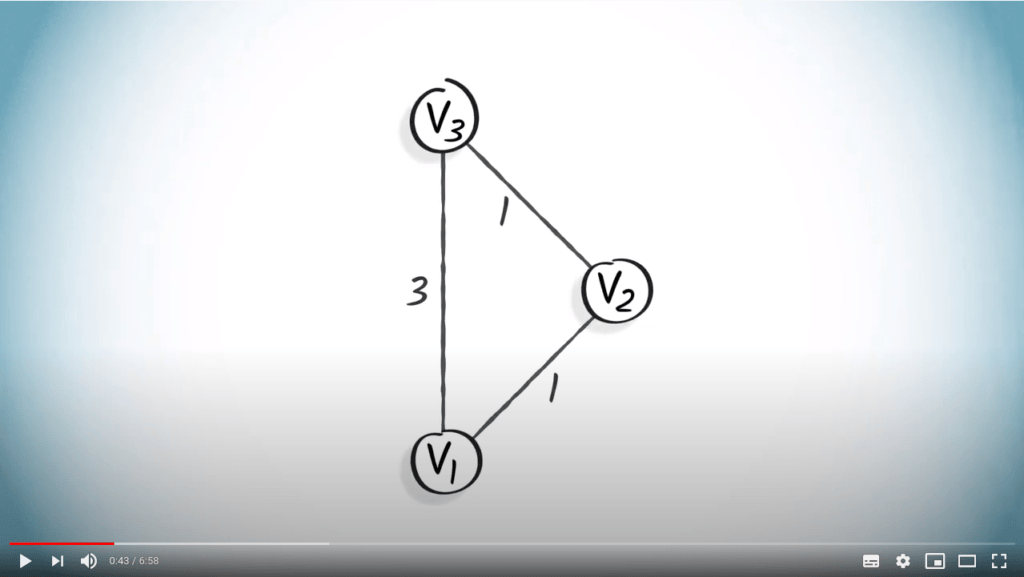
Ici, une recherche en largeur (BFS), en partant du sommet $v_1$, ne produira pas un arbre couvrant des chemins les plus courts. Par exemple, le chemin le plus court réel de $v_1$ à $v_3$ est $(\{v_1,v_2\}, \{v_2,v_3\})$, alors que le chemin trouvé en utilisant un BFS est $(\{v_1,v_3\})$.

Cela est dû au fait qu’un BFS favorise un plus petit nombre de sauts à partir du sommet initial, indépendamment des poids.

Algorithme de Dijkstra

Pour résoudre ce problème, nous introduisons l’algorithme de Dijkstra. L’algorithme de Dijkstra est une modification du BFS qui nous permet de trouver les chemins les plus courts, même en présence de poids, si ceux-ci sont non négatifs.

Une petite note sur les poids. Jusqu’à présent dans ce MOOC, nous n’avons considéré que des poids non négatifs. Dans certains cas, il pourrait être pertinent d’ajouter des poids négatifs.

Par exemple, imaginez un chauffeur de taxi qui peut voyager entre des villes. Parfois, il gagne de l’argent parce qu’il a un client et parfois il en perd parce qu’il voyage seul. Nous pourrions donc considérer un graphe dont les sommets représentent des villes et les arêtes sont pondérées par le coût du voyage correspondant. Certains poids seraient alors positifs et d’autres négatifs.

Revenons aux graphes avec des poids non négatifs. La façon la plus simple de décrire l’algorithme de Dijkstra est d’imaginer le sommet de départ comme un robinet d’où l’eau s’écoule. L’eau progressera le long des sommets et traversera le graphe avec une vitesse inversement proportionnelle aux poids des arêtes, atteignant ainsi les sommets les plus proches en premier.

En d’autres termes, l’algorithme de Dijkstra est un algorithme de parcours dans lequel les sommets sont visités par distance croissante à partir du sommet initial.

À chaque étape, l’algorithme de Dijkstra stocke deux types d’informations :

  1. quels sommets ont déjà été explorés ; et
  2. une approximation des distances de $v_1$ à tous les autres sommets du graphe.

L’algorithme de Dijkstra répète deux étapes. À l’étape 1, il sélectionne un sommet non exploré $v$ qui est à une distance minimale de $v_1$. À l’étape 2, il met à jour les distances de $v_1$ vers les autres sommets du graphe, en utilisant les informations sur $v$ et ses voisins.

Notez que l’algorithme produit toujours un arbre couvrant des chemins minimaux dans le graphe, à condition que les poids soient non négatifs. Nous n’allons pas prouver ce résultat ici, mais ce serait un excellent exercice si vous souhaitez approfondir les concepts décrits dans cette leçon.

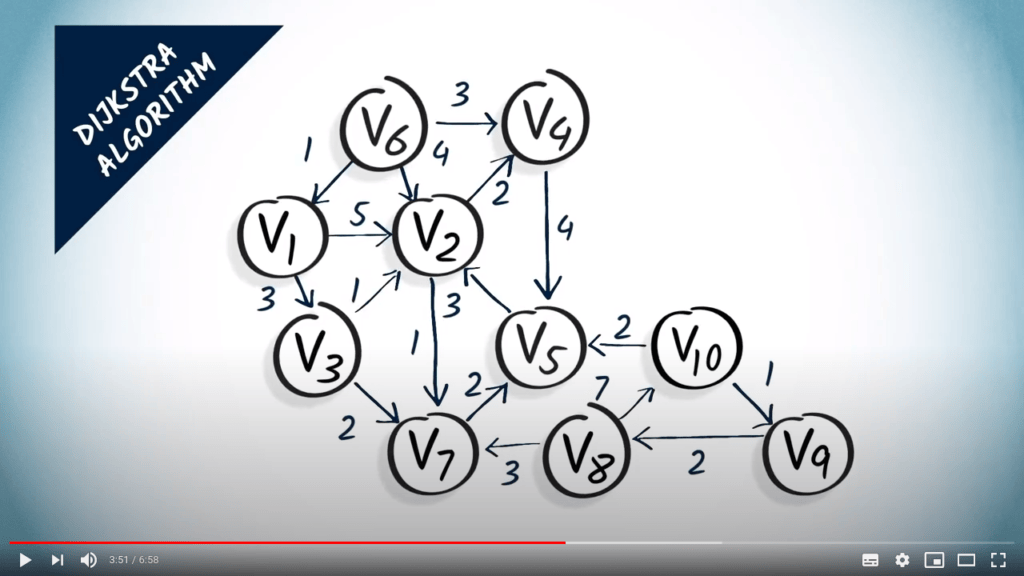
Décrivons plus précisément comment fonctionne l’algorithme de Dijkstra à l’aide de l’exemple suivant. Nous allons construire un arbre des plus courts chemins en partant du sommet $v_1$ dans ce graphe.

Nous initialisons deux structures de données : Premièrement, l’ensemble des sommets explorés, qui est initialement vide. Deuxièmement, le tableau des distances de $v_1$ vers les autres sommets du graphe, initialisé à $+\infty$ partout sauf pour $v_1$, où nous insérons un 0.

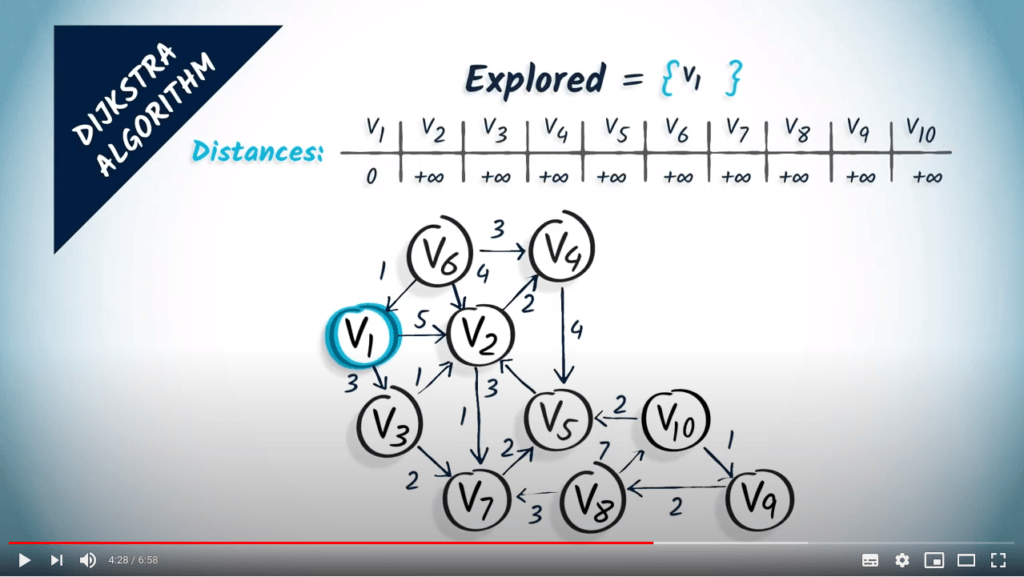
La première étape consiste à sélectionner un sommet non exploré qui est à une distance minimale du sommet de départ. Ici, nous sélectionnons $v_1$ comme sommet de départ et l’ajoutons à l’ensemble des sommets explorés.

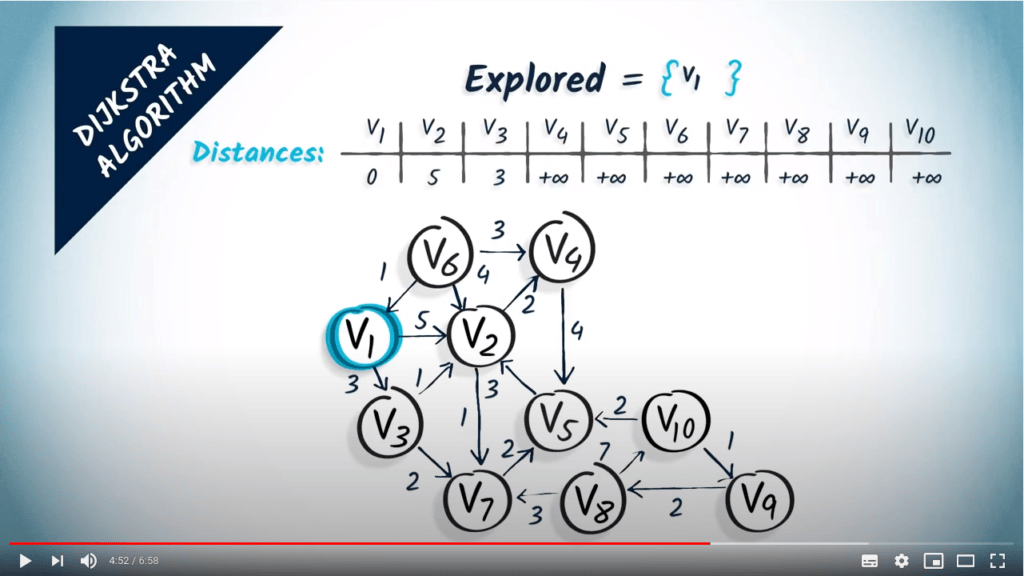
La deuxième étape consiste à mettre à jour les distances en tenant compte du sommet sélectionné $v_1$ et de ses voisins. Ici, $v_1$ a deux voisins : $v_2$ et $v_3$. Les atteindre en un saut depuis $v_1$ coûte respectivement 5 et 3. Nous mettons donc à jour nos distances depuis $v_1$ en disant que $v_2$ est à une distance de 5 et $v_3$ à une distance de 3. Notez que la longueur d’un chemin le plus court de $v_1$ à $v_2$ est en réalité 4, mais nous ne pouvons pas encore le déterminer uniquement à partir des résultats de l’algorithme.

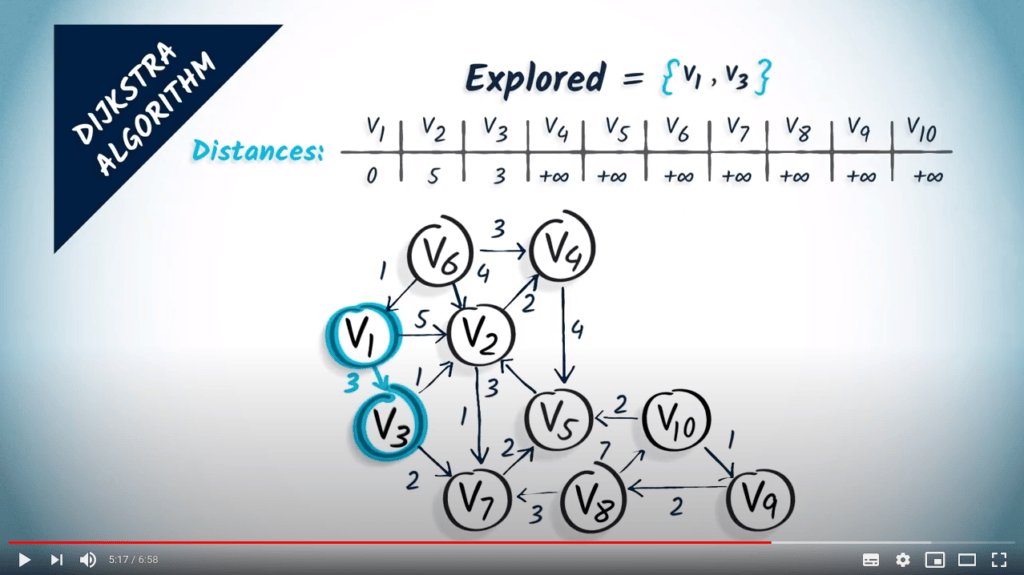
Commençons maintenant une nouvelle itération de l’algorithme. À la première étape, nous sélectionnons un sommet non exploré à une distance minimale de $v_1$. Ici, nous choisissons $v_3$, qui est à une distance de 3. Nous l’ajoutons à l’ensemble des sommets explorés.

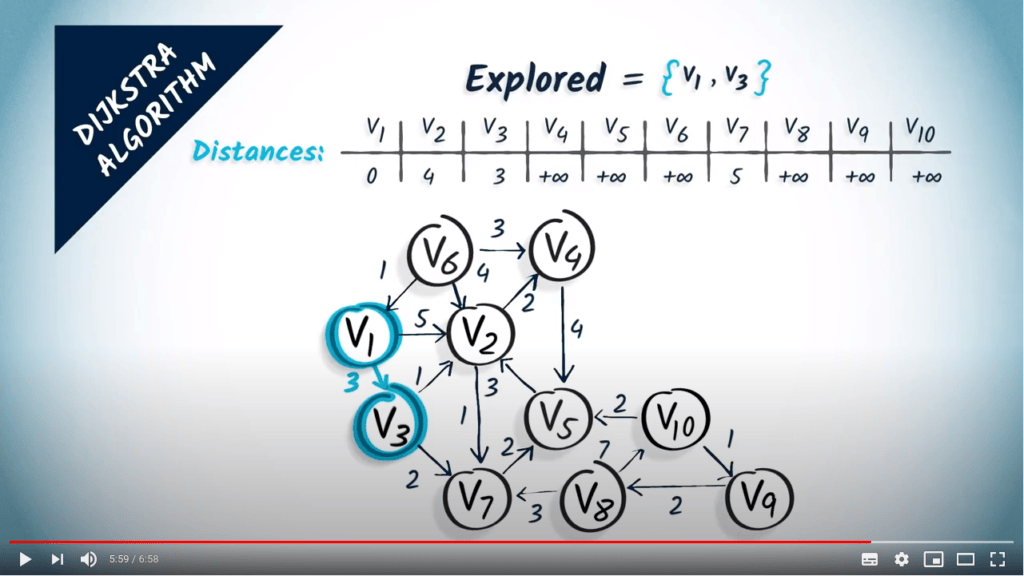
À la deuxième étape, nous examinons les voisins de $v_3$, qui sont $v_2$ et $v_7$, avec des poids correspondants de 1 et 2. Ainsi, si nous voulons atteindre $v_2$ en passant par $v_3$ un saut avant, nous avons un coût total de $3 + 1 = 4$, soit le coût pour aller à $v_3$, plus le coût d’un saut de $v_3$ à $v_2$. Cela est meilleur que la distance précédente estimée pour $v_2$, donc nous modifions les distances en conséquence. En ce qui concerne $v_7$, nous avons maintenant une distance estimée de $3 + 2 = 5$, soit le coût pour aller à $v_3$, plus le coût d’un saut de $v_3$ à $v_7$.

Une nouvelle itération commence. Maintenant, nous sélectionnons le prochain sommet non exploré avec la plus petite distance, qui est $v_2$. Nous l’ajoutons à l’ensemble des sommets explorés.

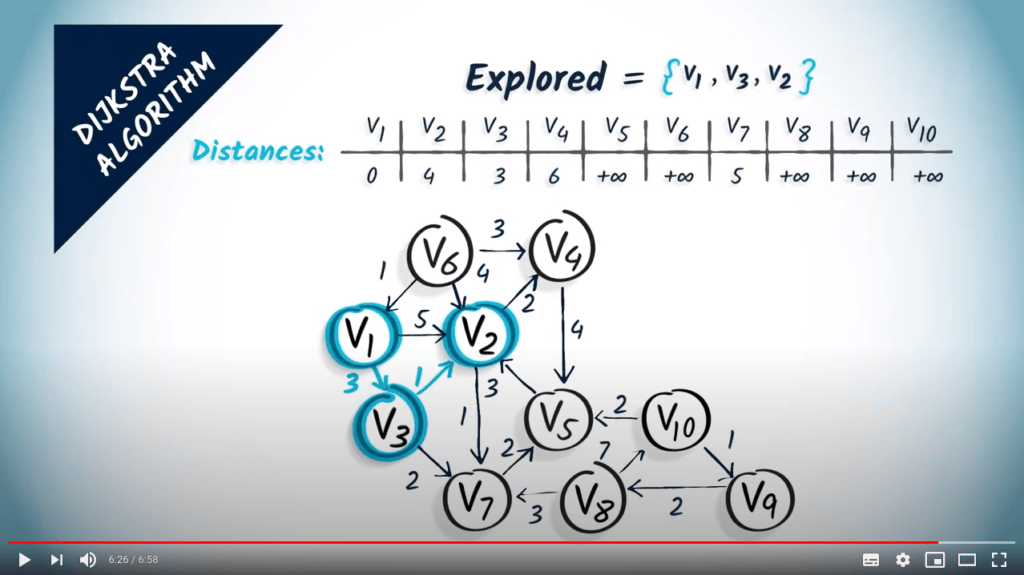
Le sommet $v_2$ a deux voisins, $v_4$ et $v_7$. Le sommet $v_4$ est estimé à une distance de $4 + 2 = 6$, et $v_7$ à une distance de $4 + 1 = 5$. Nous mettons donc à jour la distance vers $v_4$. En ce qui concerne $v_7$, la nouvelle distance trouvée n’est pas meilleure que l’ancienne, donc elle n’a aucun effet.

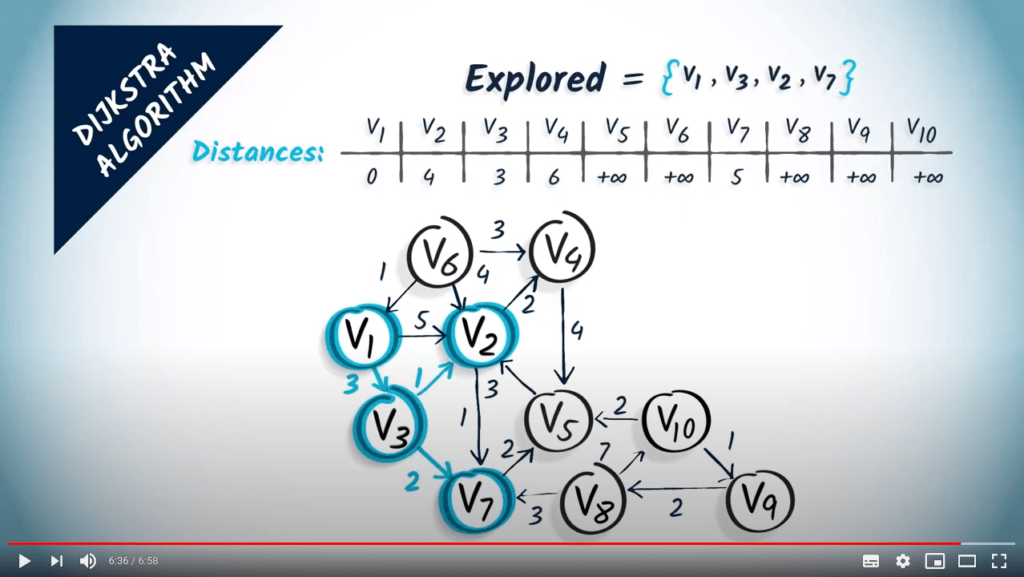
Une nouvelle itération commence. Nous sélectionnons $v_7$ à une distance de 5 et l’ajoutons à la liste des sommets explorés. Et ainsi de suite…

Finalement, nous obtenons l’arbre couvrant suivant.

Conclusion

C’est tout pour cette leçon ! Ensuite, nous verrons comment implémenter l’algorithme de Dijkstra en utilisant des tas minimaux.

Pour aller plus loin

Propriétés de l’algorithme de Dijkstra

Dans cette section, on note $n$ le nombre de sommets du graphe et $m$ son nombre d’arêtes. La longueur d’un chemin est la somme des poids de ses arêtes, et $d(u, v)$ désigne la longueur d’un plus court chemin de $u$ à $v$.

Les propriétés ci-dessous portent sur la version de l’algorithme programmée dans l’activité pratique. Elle utilise un tas min géré avec la bibliothèque heapq (voir l’article sur les tas min). Comme heapq ne sait pas remplacer un élément, un même sommet peut s’y trouver plusieurs fois, avec des distances différentes. Seul son premier retrait compte : c’est à ce moment qu’il est exploré, et ses retraits suivants sont ignorés.

Terminaison

L’algorithme de Dijkstra sur un graphe fini termine, quels que soient les poids des arêtes.

Preuve
Cliquez ici pour afficher la preuve.

La preuve est la même que pour le BFS (voir l’article sur les parcours de graphes), puisqu’elle ne dépend ni de l’ordre des retraits, ni des poids.

Un sommet n’est exploré qu’une seule fois, puisque ses retraits suivants sont ignorés. Par ailleurs, des éléments ne sont ajoutés au tas min que lors de l’exploration d’un sommet $v$, et il y en a alors $\deg(v)$ (un par voisin). Au total, en comptant le sommet de départ, le nombre d’ajouts est donc au plus :

$$1 + \sum\limits_{v \in V} \deg(v) = 1 + 2m$$

Comme chaque itération retire un élément du tas min, il y a au plus $1 + 2m$ itérations. L’algorithme termine donc.

Correction

Si tous les poids du graphe sont positifs ou nuls, l’algorithme de Dijkstra retourne un plus court chemin entre un sommet $u$ et tous les autres sommets atteignables depuis $u$.

C’est le cas dans PyRat, où toutes les arêtes ont un poids d’au moins 1. Nous verrons plus bas ce qui se passe lorsque certains poids sont négatifs.

Preuve
Cliquez ici pour afficher la preuve.

Pour chaque sommet exploré $v$, notons $D(v)$ la distance de l’élément retiré lors de son exploration. C’est la valeur distances[vertex] calculée dans le code de l’activité pratique. Notons aussi $w(x, y)$ le poids de l’arête $\{x,y\}$.

Nous allons montrer que :

  • Tous les sommets atteignables sont explorés.
  • Pour tout sommet exploré $v$, la table de routage donne un chemin de $u$ à $v$ de longueur $D(v)$.
  • Pour tout sommet exploré $v$, $D(v) = d(u, v)$, c’est-à-dire que ce chemin est de longueur minimale.

Tous les sommets atteignables sont explorés

L’argument est le même que pour le BFS. Lorsqu’un sommet est exploré, tous ses voisins sont ajoutés au tas min. Comme l’algorithme ne s’arrête que lorsque le tas min est vide, chacun d’eux finira par en être retiré, et donc par être exploré (s’il ne l’a pas été entre-temps). En suivant un chemin de $u$ à un sommet atteignable $v$, on conclut par induction que $v$ est exploré.

La table de routage donne un chemin de longueur $D(v)$

Montrons-le par induction, dans l’ordre d’exploration. C’est vrai pour $u$, avec $D(u) = 0$. Un autre sommet $v$ est exploré lors du retrait d’un élément ajouté par un voisin $p$, exploré avant lui, qui devient son parent. Cet élément a pour distance $D(p) + w(p, v)$. Par hypothèse d’induction, la table de routage donne un chemin de $u$ à $p$ de longueur $D(p)$, et il suffit d’y ajouter l’arête $\{p,v\}$ pour obtenir un chemin de $u$ à $v$ de longueur $D(p) + w(p, v) = D(v)$.

En particulier, $D(v)$ est la longueur d’un chemin de $u$ à $v$, donc $D(v) \geq d(u, v)$.

Les chemins obtenus sont de longueur minimale

Montrons l’inégalité inverse par l’absurde. Supposons qu’il existe des sommets explorés tels que $D(v) > d(u, v)$, et choisissons pour $v$ le premier d’entre eux dans l’ordre d’exploration. On a $v \neq u$, car $D(u) = 0 = d(u, u)$.

Considérons un plus court chemin de $u$ à $v$, et plaçons-nous juste avant l’itération qui explore $v$. À ce moment, $u$ est déjà exploré, mais pas $v$. Notons $y$ le premier sommet du chemin qui n’est pas encore exploré (éventuellement $v$ lui-même), et $x$ le sommet qui le précède sur le chemin. Alors :

  • Le sommet $x$ a été exploré avant $v$, donc par choix de $v$, $D(x) = d(u, x)$.
  • Lors de l’exploration de $x$, un élément concernant $y$ a été ajouté au tas min, avec la distance $d(u, x) + w(x, y)$. Comme le début d’un plus court chemin est lui-même un plus court chemin, cette distance vaut $d(u, y)$.
  • Cet élément n’a pas encore été retiré, sinon $y$ serait déjà exploré. Il est donc toujours dans le tas min.
  • Les poids étant positifs ou nuls, la fin du chemin, de $y$ à $v$, a une longueur positive ou nulle. Donc $d(u, y) \leq d(u, v)$.

Or, l’itération qui explore $v$ retire l’élément de plus petite distance du tas min, et cette distance est $D(v)$. On a donc $D(v) \leq d(u, y) \leq d(u, v)$, ce qui contredit l’hypothèse. Le chemin obtenu pour chaque sommet atteignable est donc un plus court chemin.

Notez que l’hypothèse sur les poids n’est utilisée qu’à la dernière étape : avec un poids négatif, la fin du chemin pourrait réduire la distance, et l’argument ne tiendrait plus.

Complexité

Avec le tas min de heapq, l’algorithme de Dijkstra a une complexité de $O((n + m) \cdot log(n))$.

Dans un labyrinthe PyRat, on a $m < 2n$ (voir l’article sur les graphes), et la complexité est donc $O(n \cdot log(n))$. C’est un peu plus que le $O(n)$ du BFS, mais cela reste tout à fait raisonnable pour notre problème.

Preuve
Cliquez ici pour afficher la preuve.

D’après la preuve de terminaison, il y a au plus $1 + 2m$ ajouts dans le tas min, et donc au plus $1 + 2m$ retraits. Le tas min contient ainsi à tout moment au plus $1 + 2m$ éléments, et chaque ajout ou retrait coûte $O(log(m))$ opérations (voir l’article sur les tas min).

Comme un graphe a au plus une arête par paire de sommets, on a $m \leq n^2$, donc $log(m) \leq 2 \cdot log(n)$. Les ajouts et retraits coûtent donc $O(m \cdot log(n))$ opérations au total.

Le reste du décompte est le même que pour le BFS : chaque sommet est exploré au plus une fois, et son exploration parcourt ses $\deg(v)$ voisins, soit $O(n + m)$ opérations au total.

La complexité est donc $O((n + m) \cdot log(n))$.

Important

Cette complexité dépend de la file de priorité utilisée :

  • Avec le tas min naïf basé sur une liste, présenté dans l’article sur les tas min, chaque ajout et chaque retrait coûte $O(n)$ opérations. La complexité devient alors $O(n \cdot (n + m))$, soit $O(n^2)$ dans un labyrinthe PyRat.

  • Avec un tas de Fibonacci, ajouter un élément ou diminuer sa distance se fait en temps constant (en moyenne sur l’ensemble des opérations), et seul le retrait coûte $O(log(n))$ opérations. La complexité devient alors $O(m + n \cdot log(n))$. C’est la meilleure complexité connue pour cet algorithme, mais ce tas est délicat à programmer, et ses constantes élevées le rendent rarement plus rapide que heapq en pratique.

Le cas des poids négatifs

Lorsque certains poids sont négatifs, l’algorithme de Dijkstra termine toujours, mais les chemins obtenus ne sont plus forcément les plus courts.

Considérons un graphe orienté (voir l’article sur les graphes) formé de trois sommets $u$, $a$ et $b$, avec un arc $(u,a)$ de poids 2, un arc $(u,b)$ de poids 3, et un arc $(b,a)$ de poids $-2$. Lançons l’algorithme de Dijkstra depuis $u$ :

  • On explore $u$, et on ajoute au tas min $a$ avec la distance 2, et $b$ avec la distance 3.
  • On retire $a$, qui a la plus petite distance. On l’explore, avec $D(a) = 2$.
  • On retire $b$. On l’explore, et on ajoute $a$ au tas min, avec la distance $3 - 2 = 1$.
  • On retire $a$, mais il est déjà exploré : ce retrait est ignoré.

L’algorithme indique donc que $a$ est à une distance 2 de $u$, alors que le chemin passant par $b$ a une longueur de 1. Le problème vient de ce qu’un sommet exploré est considéré comme définitivement traité. Avec des poids positifs ou nuls, aucun chemin découvert plus tard ne peut être plus court. Avec un arc de poids négatif, si.

Dans un graphe non orienté, c’est encore pire. Une arête de poids négatif peut être parcourue en aller-retour autant de fois qu’on le souhaite, et chaque aller-retour diminue la longueur totale : on peut donc construire des marches aussi courtes que l’on veut. C’est ce qu’on appelle un cycle absorbant.

Pour traiter des poids négatifs, il faut utiliser un autre algorithme, comme l’algorithme de Bellman-Ford, présenté dans l’activité pratique. Dans PyRat, tous les poids sont positifs, et l’algorithme de Dijkstra convient parfaitement.

Arrêter le parcours plus tôt

Dans PyRat, on cherche souvent le chemin vers une seule case : celle du fromage. Or, d’après la preuve de correction, dès qu’un sommet est exploré, sa distance et son chemin dans la table de routage sont définitifs. On peut donc arrêter l’algorithme dès que la cible est explorée, sans attendre que le tas min soit vide.

Il suffit d’ajouter un paramètre target à la méthode traversal(...) de l’activité pratique, et de sortir de la boucle au bon moment (dans la version factorisée, c’est déjà le rôle du paramètre stop_vertices de Traversal) :

​
# Update the distances and routing table
distances[vertex] = distance
routing_table[vertex] = parent

# Stop as soon as the target is explored
if vertex == target:
    break

Les sommets plus éloignés de $u$ que la cible ne sont alors pas explorés, ce qui fait gagner beaucoup de temps lorsque le fromage est proche. La complexité dans le pire cas reste cependant la même, puisque la cible peut être le sommet le plus éloigné de $u$.

Cette idée est le point de départ de l’algorithme A*, qui va plus loin en explorant en priorité les sommets qui semblent se rapprocher de la cible (voir la section « Pour aller encore plus loin »).

Récapitulatif

BFS DFS Dijkstra
Structure de données FIFO (file) LIFO (pile) Tas min (file de priorité)
Termine sur un graphe fini Oui Oui Oui
Explore tous les sommets atteignables Oui Oui Oui
Donne des plus courts chemins Si graphe non pondéré Pas nécessairement Si poids positifs ou nuls
Complexité $O(n + m)$ $O(n + m)$ $O((n + m) \cdot log(n))$
Structure conseillée en Python collections.deque list heapq

Dans un graphe dont toutes les arêtes ont le même poids, l’algorithme de Dijkstra trouve les mêmes distances que le BFS, mais avec une complexité plus élevée. Dans un labyrinthe sans boue, le BFS reste donc le meilleur choix.

Pour aller encore plus loin

  • Une structure de données pour améliorer le temps d’exécution de l’algorithme de Dijkstra.
  • Une présentation interactive qui passe du BFS à l’algorithme de Dijkstra, puis à A*, pour atteindre une cible plus rapidement.