Activité pratique
Durée2h30Consignes globales
Cette activité étend la précédente en proposant d’implémenter de nouveaux algorithmes de parcours de graphe, qui permettent de trouver des chemins dans un graphe pondéré. Nous allons travailler avec la configuration suivante :
- Un seul joueur.
- Un seul morceau de fromage à attraper.
- On ajoute de la boue dans le labyrinthe (20-30% des arêtes).
Cette séance sera moins guidée que la précédente, et ce sera de plus en plus le cas à mesure que vous avancerez dans le projet. Nous restons néanmoins disponibles pour vous aider si vous avez des questions, en classe ou sur Discord.
Contenu de l’activité
1 — Algorithme de Dijkstra
1.1 — Préparation
Tout d’abord, nous allons créer un joueur et un script pour visualiser son comportement.
Avant de commencer, créez les fichiers nécessaires dans votre workspace PyRat en suivant les instructions ci-dessous.
Comme indiqué dans les instructions, vous devez créer une classe héritant de Player, nommée Dijkstra, dans un fichier Dijkstra.py dans le sous-dossier players de pyrat_workspace.
Faites attention à ce que turn(...) renvoie bien une action (qui peut être Action.NOTHING).
Pensez aussi à mettre à jour les documentations pour que ça corresponde au futur code.
Globalement, le code ressemblera beaucoup à celui de DFS.py ou BFS.py.
Si vous partez d’un de ces fichiers, ça vous fera sûrement gagner du temps.
Vous devez également créer un script visualize_Dijkstra.py dans le sous-dossier games.
Attention à bien fixer les arguments mud_percentage et nb_cheese du constructeur de la classe Game.
Le fichier devrait ressembler à ça :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import pprint
# PyRat imports
from pyrat import Game
from players.Dijkstra import Dijkstra
##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################
if __name__ == "__main__":
# Instantiate a game with a few arguments
game_config = {"mud_percentage": 20.0,
"maze_width": 13,
"maze_height": 10,
"nb_cheese": 1,
"random_seed": 42,
"trace_length": 1000}
# Instantiate a game with specified arguments
game = Game(**game_config)
# Instantiate the player
player = Dijkstra()
game.add_player(player)
# Start the game
stats = game.start()
pprint.pprint(stats)
##########################################################################################
##########################################################################################Enfin, vous devez créer un fichier de tests unitaires test_Dijkstra.py dans le sous-dossier tests.
Pour le moment, créez juste le fichier avec une classe Dijkstra_Tests copiée-collée de test_DFS.py ou test_BFS.py, en changeant le nom de la classe et en enlevant les méthodes de test.
La correction de ce fichier est disponible plus bas.
-
players/Dijkstra.py– Inspirez vous de ce que vous avez fait lors des séances précédentes pour créer un joueurDijkstrahéritant dePlayer, et ayant :- Un constructeur
__init__(...). - Une méthode
preprocessing(...). - Une méthode
turn(...).
Dans un premier temps, ne vous préoccupez pas du comportement de votre joueur, créez juste le strict minimum pour pouvoir lancer une partie avec votre joueur
Dijkstrasans que ça crashe. - Un constructeur
-
games/visualize_Dijkstra.py– Créez un fichier qui lancera une partie avec un joueurDijkstra, dans un labyrinthe respectant les critères listés plus haut. Vous pouvez éventuellement définir unerandom_seed(pour toujours travailler avec le même labyrinthe) et unetrace_length(pour suivre la trajectoire de votre joueur). Inspirez-vous des autres fichiers du sous-dossiergamesque vous avez rencontrés lors des séances précédentes. -
tests/tests_Dijkstra.py– En vous inspirant des fichierstest_DFS.pyettest_BFS.pyrencontrés lors de la séance précédente, créez un fichiertest_Dijkstra.py. Ce fichier contiendra les tests unitaires que vous développerez pour tester les fonctions définies dansDijkstra.py.
1.2 — Programmer l’algorithme de Dijkstra
L’objectif principal de cette séance est d’implémenter l’algorithme de Dijkstra pour guider votre personnage dans le labyrinthe. En effet, maintenant que nous avons de la boue dans le labyrinthe, un simple parcours en largeur (BFS) ne suffit plus pour trouver le chemin le plus rapide vers le fromage.
À l’aide des scripts développés dans la séance précédente, visualisez le comportement d’un joueur BFS dans un labyrinthe avec de la boue.
Quel est le souci ?
Reprenez le script visualize_BFS.py de la séance précédente, et modifiez les arguments du constructeur de Game pour avoir de la boue.
Par exemple, prenez mud_percentage=20.0.
Le joueur BFS ne prend pas en compte les coûts de déplacement différents.
Il ne distingue pas entre un chemin avec de la boue et un chemin sans boue.
Il trouvera donc le chemin le plus court en nombre de cases, mais pas nécessairement le chemin le plus rapide en termes de temps de déplacement.
1.2.1 — Identifier les fonctions
La dernière fois, en programmant les algorithmes BFS et DFS, nous avons identifié quelques tâches pour lesquelles nous avons créé des fonctions dédiées : les méthodes traversal(...) et find_route(...).
Séparer ces deux blocs nous a permis d’écrire plus facilement des tests unitaires et d’obtenir un code pleinement fonctionnel.
Prenez d’abord un moment pour réfléchir aux méthodes nécessaires pour écrire l’algorithme de Dijkstra. Quels devraient être leurs paramètres d’entrée ? Et quelles sorties devraient-elles produire ?
Une fois cela fait, écrivez leurs prototypes (i.e., la ligne def ..., et un return ... temporaire si nécessaire) dans votre fichier Dijkstra.py.
Comme pour DFS et BFS, on peut identifier deux tâches principales :
-
Un parcours du graphe pondéré à partir d’une source, pour déterminer le plus court chemin vers tous les autres sommets. C’est la méthode
traversal(...). Elle prend en entrée un graphe, une source, et éventuellement une liste de sommets à atteindre. Elle renvoie un dictionnaire des prédécesseurs de chaque sommet visité, et éventuellement le sommet atteint dans la liste. -
Une fois qu’on a le dictionnaire des prédécesseurs, on peut reconstruire le chemin le plus court entre la source et une cible. C’est la méthode
find_route(...). Elle prend en entrée le dictionnaire des prédécesseurs, une source, et une cible. Elle renvoie une liste de sommets représentant le chemin de la source à la cible.
Les prototypes de ces méthodes sont les mêmes que pour DFS et BFS.
1.2.2 — Réfléchir aux tests unitaires
Pour programmer vos fonctions, vous pouvez choisir entre deux approches :
-
Approche classique – La méthode la plus courante pour développer un programme est de programmer le corps d’une méthode, puis de la tester. Une fois validée, passez à la méthode suivante, etc., jusqu’à ce que toutes les méthodes soient programmées.
-
Développement piloté par les tests – Si vous préférez, avant de coder le contenu de vos méthodes, vous pouvez déjà écrire les tests unitaires dans
test_Dijkstra.py. Cela vous permettra de tester vos méthodes plus fréquemment pendant leur développement, et vous pourrez être convaincu de votre travail lorsqu’elles passeront tous les tests que vous avez conçus.
Que vous les écriviez avant ou après le code, il est important de concevoir des tests qui vous convainquent que votre programme fonctionne comme prévu !
Par exemple, supposons que vous souhaitiez concevoir un test pour vous assurer que Dijkstra trouve le chemin le plus court dans un graphe pondéré, contrairement à un BFS. Intuitivement, vous voulez créer un graphe fixe, identifier le chemin le plus court à la main, et vérifier que la sortie de Dijkstra correspond à ce chemin. Cependant, le choix du graphe utilisé a une grande importance :
-
Si vous choisissez un labyrinthe dans lequel il n’y a qu’un seul chemin entre votre position initiale et le morceau de fromage, alors les algorithmes BFS et Dijkstra trouveront tous deux le chemin correct.
-
De même, s’il n’y a pas de boue le long du chemin le plus court entre votre position initiale et le morceau de fromage (ou s’il est toujours plus rapide de traverser cette boue que de l’éviter), alors encore une fois, les algorithmes BFS et Dijkstra trouveront le chemin correct.
Prenez un moment pour réfléchir et lister les tests unitaires que vous souhaitez effectuer. Pour chaque test, déterminez s’il correspond à une utilisation normale ou à une erreur possible.
Pour la méthode traversal(...) :
-
Quelques idées de tests d’utilisation normale :
- Tester avec des graphes non pondérés (tous les poids égaux) et comparer la longueur des chemins trouvés avec
BFS. - Tester avec des graphes pondérés contrôlés où on connaît déjà les plus courts chemins.
- Tester avec des graphes pondérés plus complexes, et vérifier que la longueur des chemins trouvés est toujours inférieure ou égale à celle des chemins trouvés par
BFS.
- Tester avec des graphes non pondérés (tous les poids égaux) et comparer la longueur des chemins trouvés avec
-
Quelques idées de tests d’erreurs possibles, qui devraient lever des exceptions :
- Tester avec une source qui n’existe pas dans le graphe.
- Tester avec des poids négatifs.
- Appeler la méthode avec des arguments de types incorrects (par exemple, une chaîne au lieu d’un graphe).
-
Quelques idées de tests en dehors des clous, mais qui devraient quand même fonctionner :
- Tester avec un graphe non connexe. On devrait toujours obtenir les plus courts chemins pour les sommets atteignables.
Pour la méthode find_route(...) :
-
Quelques idées de tests d’utilisation normale :
- Tester avec des prédécesseurs valides et vérifier que le chemin renvoyé est correct.
- Tester avec la source égale à la cible, et vérifier que le chemin renvoyé est juste la source.
- Tester avec une cible qui n’est pas atteignable depuis la source, et vérifier que le chemin renvoyé est vide.
-
Quelques idées de tests d’erreurs possibles, qui devraient lever des exceptions :
- Tester avec une source ou une cible qui n’existent pas dans le dictionnaire des prédécesseurs.
- Appeler la méthode avec des arguments de types incorrects (par exemple, une liste au lieu d’un dictionnaire).
-
Quelques idées de tests en dehors des clous, mais qui devraient quand même fonctionner :
- Tester avec un dictionnaire des prédécesseurs qui ne couvre pas tous les sommets du graphe. On devrait toujours obtenir un chemin correct si la cible est atteignable.
1.2.3 — Programmer et tester
Maintenant que vous avez identifié les fonctions nécessaires et les tests unitaires que vous souhaitez effectuer, programmez vos fonctions dans Dijkstra.py et vos tests dans test_Dijkstra.py.
N’oubliez pas d’exécuter fréquemment vos tests unitaires pour vous assurer que votre code fonctionne comme prévu.
À terme, le joueur devrait ressembler à ça :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import heapq
# PyRat imports
from pyrat import Player, Maze, GameState, Action, Graph
##########################################################################################
######################################### CLASSES ########################################
##########################################################################################
class Dijkstra (Player):
"""
*(This class inherits from* ``Player`` *).*
This player performs Dijkstra's algorithm to find the shortest path in the maze.
Computation of the path is done in the ``preprocessing(...)`` method.
The path is then followed in the ``turn(...)`` method.
"""
##################################################################################
# CONSTRUCTOR #
##################################################################################
def __init__ ( self,
*args: object,
**kwargs: object
) -> None:
"""
Initializes a new instance of the class.
Args:
args: Arguments to pass to the parent constructor.
kwargs: Keyword arguments to pass to the parent constructor.
"""
# Inherit from parent class
super().__init__(*args, **kwargs)
# We create an attribute to store the actions to perform
self.actions = None
##################################################################################
# PYRAT METHODS #
##################################################################################
def preprocessing ( self,
maze: Maze,
game_state: GameState,
) -> None:
"""
*(This method redefines the method of the parent class with the same name).*
This method is called once at the beginning of the game.
Here, we use Dijkstra's algorithm to compute a shortest path that reaches the piece of cheese from the initial position of the player.
The actions corresponding to the path are stored in the ``actions`` attribute, and will be used in the ``turn(...)`` method.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
"""
# We perform a traversal of the maze graph from the initial position of the player
my_location = game_state.player_locations[self.get_name()]
distances, routing_table = self.traversal(maze, my_location)
# Find the series of locations/actions to go from the player location to the first piece of cheese
path = self.find_route(routing_table, my_location, game_state.cheese[0])
self.actions = maze.locations_to_actions(path)
##################################################################################
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
"""
*(This method redefines the method of the parent class with the same name).*
It is called at each turn of the game.
It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
The action is chosen by following the path computed in the ``preprocessing(...)`` method.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
Returns:
One of the possible actions.
"""
# At each turn, we perform the next action in the list of actions
return self.actions.pop(0)
##################################################################################
# OTHER METHODS #
##################################################################################
def traversal ( self,
graph: Graph,
source: int
) -> tuple[dict[int, int], dict[int, int | None]]:
"""
This method performs Dijkstra's algorithm on a graph.
It returns the explored vertices with associated distances.
It also returns the routing table, that is, the parent of each vertex in the traversal.
Args:
graph: The graph to traverse.
source: The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).
Returns:
A tuple containing:
- The distances from the source to each explored vertex.
- The routing table, that is, the parent of each vertex in the traversal (None for the source).
"""
# Initialization
distances = {}
routing_table = {}
# Initialize the list of vertices to visit
vertices_to_visit = []
heapq.heappush(vertices_to_visit, (0, source, None))
# Traversal
while vertices_to_visit:
# Get the next vertex to visit
distance, vertex, parent = heapq.heappop(vertices_to_visit)
# Skip if already visited
# This can happen if a vertex was added multiple times to the list by different neighbors
if vertex in distances:
continue
# Update the distances and routing table
distances[vertex] = distance
routing_table[vertex] = parent
# Add the neighbors to the list of vertices to visit
for neighbor in graph.get_neighbors(vertex):
distance_to_neighbor = distances[vertex] + graph.get_weight(vertex, neighbor)
heapq.heappush(vertices_to_visit, (distance_to_neighbor, neighbor, vertex))
# Return the result
return distances, routing_table
##################################################################################
def find_route ( self,
routing_table: dict[int, int | None],
source: int,
target: int
) -> list[int]:
"""
This method finds the route from a source vertex to a target vertex using a routing table.
Args:
routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
source: The source vertex.
target: The target vertex.
Returns:
The route from the source to the target as a list of vertices.
"""
# Initialization
route = [target]
vertex = target
# Find the route
while vertex != source:
vertex = routing_table[vertex]
route.append(vertex)
# Reverse the route
route.reverse()
return route
##########################################################################################
##########################################################################################Et voici quelques tests, directement adaptés de ceux développés pour tester le BFS. On pourrait bien sur ajouter d’autres tests pour une meilleure couverture, comme par exemple vérifier que Dijkstra trouve bien un chemin de longueur inférieure ou égale à celui trouvé par BFS dans un graphe pondéré. On pourrait également ajouter des tests pour les erreurs possibles listées plus haut.
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import random
import unittest
# PyRat imports
from pyrat import MazeFromDict, RandomMaze, RandomMazeAlgorithm, BigHolesRandomMaze, HolesOnSideRandomMaze, UniformHolesRandomMaze
from players.Dijkstra import Dijkstra
##########################################################################################
######################################### CLASSES ########################################
##########################################################################################
class Dijkstra_Tests (unittest.TestCase):
"""
*(This class inherits from* ``unittest.TestCase`` *).*
This class tests the methods of the Dijkstra class.
For each method, we test it with a few different configurations.
"""
##################################################################################
# INITIALIZATION #
##################################################################################
def setUp (self) -> None:
"""
This method is called before each test method.
It allows to factorize attributes that are common to all test methods.
It is basically acting as a constructor, but it is called before each test method, not only once when the class is instantiated.
"""
# Nothing to do here
pass
##################################################################################
# CLEANUP #
##################################################################################
def tearDown (self) -> None:
"""
This method is called after each test method.
It allows to clean up any resources that were allocated in the `setUp(...)` method.
"""
# Nothing to do here
pass
##################################################################################
# AUXILIARY METHODS #
##################################################################################
def create_random_maze ( self,
maze_type: RandomMazeAlgorithm,
maze_arguments: dict[str, object] = {}
) -> RandomMaze:
"""
Create a random maze using the specified algorithm
Args:
maze_type: The type of random maze to create.
maze_arguments: Additional arguments to pass to the maze constructor.
Returns:
A random maze of the specified type.
"""
# We create a maze
if maze_type == RandomMazeAlgorithm.HOLES_ON_SIDE:
maze = HolesOnSideRandomMaze(**maze_arguments)
elif maze_type == RandomMazeAlgorithm.UNIFORM_HOLES:
maze = UniformHolesRandomMaze(**maze_arguments)
elif maze_type == RandomMazeAlgorithm.BIG_HOLES:
maze = BigHolesRandomMaze(**maze_arguments)
return maze
##################################################################################
# TESTS #
##################################################################################
def test_traversal_random (self) -> None:
"""
This method tests the ``traversal(...)`` method.
We are going to check the following:
- Outputs are of the expected types.
- All vertices are visited.
- The routing table is a tree, with root corresponding to the start of the traversal.
- The found distances are correct, i.e., strictly positive and increasing, except for the start vertex which should be 0.
Note that we cannot test that the output is unique, as there are multiple valid outputs, depending on how vertices are explored.
We will test the method on several random graphs to make sure it is working properly.
Random graphs will be generated using the PyRat class used to create mazes in games.
There are several such classes, but we will use the BigHolesRandomMaze class.
"""
# Constants
NB_GRAPHS = 10
WIDTHS = [2, 30]
HEIGHTS = [2, 30]
CELL_PERCENTAGES = [20.0, 100.0]
WALL_PERCENTAGES = [20.0, 100.0]
MUD_RANGE = [2, 10]
MUD_PERCENTAGE = 60.0
# Test on several graphs
for i in range(NB_GRAPHS):
# Instantiate the player
player = Dijkstra()
# Generate a random maze
# We use a fixed random seed for reproducibility of tests
rng = random.Random(i)
config = {"width": rng.randint(WIDTHS[0], WIDTHS[1]),
"height": rng.randint(HEIGHTS[0], HEIGHTS[1]),
"cell_percentage": rng.uniform(CELL_PERCENTAGES[0], CELL_PERCENTAGES[1]),
"wall_percentage": rng.uniform(WALL_PERCENTAGES[0], WALL_PERCENTAGES[1]),
"mud_range": MUD_RANGE,
"mud_percentage": MUD_PERCENTAGE,
"random_seed": i}
maze = self.create_random_maze(RandomMazeAlgorithm.BIG_HOLES, config)
# Choose a random starting vertex
start_vertex = rng.choice(maze.get_vertices())
# Perform the traversal
distances, routing_table = player.traversal(maze, start_vertex)
# Check the output type for distances
# It should be a dictionary with integer keys and integer values
self.assertTrue(isinstance(distances, dict))
self.assertTrue(all(isinstance(k, int) for k in distances.keys()))
self.assertTrue(all(isinstance(v, int) for v in distances.values()))
# Check the output type for the routing table
# It should be a dictionary with integer keys and integer or None values
self.assertTrue(isinstance(routing_table, dict))
self.assertTrue(all(isinstance(k, int) for k in routing_table.keys()))
self.assertTrue(all(isinstance(v, (type(None), int)) for v in routing_table.values()))
# All vertices should be visited
# Equivalently, the distances should have the same keys as the maze vertices
self.assertEqual(sorted(set(distances.keys())), sorted(maze.get_vertices()))
# Check that the start vertex is the only tree root
self.assertEqual(routing_table[start_vertex], None)
self.assertTrue(all(routing_table[v] is not None for v in routing_table.keys() if v != start_vertex))
self.assertEqual(distances[start_vertex], 0)
self.assertTrue(all(distances[v] > 0 for v in distances.keys() if v != start_vertex))
# We check that the routing table is a tree
# Also we check that associated distances are decreasing as we go to the root
for vertex in routing_table:
# We check that the parent is closer to the root
if routing_table[vertex] is not None:
self.assertTrue(distances[routing_table[vertex]] < distances[vertex])
# We ckeck that we can reach the root from any vertex
path = [vertex]
while routing_table[path[-1]] is not None:
self.assertTrue(routing_table[path[-1]] not in path)
path.append(routing_table[path[-1]])
##################################################################################
def test_traversal_fixed (self) -> None:
"""
This method complements the previous tests by testing the `traversal(...)` method on some controlled examples.
To do so, we will use some mazes for which there is a unique routing table.
We do not test the output types again, as it has already been done in the previous test function.
"""
# Constants
TESTS = [{"inputs": {"maze": MazeFromDict({0: {15: 1}, 1: {16: 8}, 6: {7: 1, 21: 1}, 7: {6: 1}, 8: {9: 1, 23: 1}, 9: {8: 1, 10: 1}, 10: {9: 1}, 11: {12: 1, 26: 1}, 12: {11: 1, 13: 1}, 13: {12: 1}, 14: {29: 6}, 15: {0: 1, 16: 1, 30: 1}, 16: {15: 1, 1: 8}, 21: {6: 1, 36: 1, 22: 8}, 22: {23: 1, 21: 8}, 23: {8: 1, 22: 1, 38: 1}, 25: {26: 1}, 26: {11: 1, 25: 1, 41: 9}, 28: {29: 4}, 29: {44: 1, 14: 6, 28: 4}, 30: {15: 1, 45: 1}, 31: {46: 5, 32: 4}, 32: {31: 4}, 34: {35: 1}, 35: {34: 1, 36: 1}, 36: {21: 1, 35: 1}, 37: {52: 1}, 38: {23: 1, 53: 1}, 40: {41: 1}, 41: {40: 1, 56: 1, 26: 9}, 44: {29: 1, 59: 1}, 45: {30: 1, 46: 1, 60: 1}, 46: {45: 1, 47: 1, 61: 1, 31: 5}, 47: {46: 1, 48: 1, 62: 4}, 48: {47: 1}, 49: {64: 8}, 50: {65: 4}, 52: {37: 1, 53: 1}, 53: {38: 1, 52: 1, 68: 4}, 55: {56: 1, 70: 1}, 56: {41: 1, 55: 1}, 57: {58: 1, 72: 1}, 58: {57: 1, 59: 1}, 59: {44: 1, 58: 1}, 60: {45: 1}, 61: {46: 1}, 62: {63: 1, 47: 4}, 63: {62: 1, 78: 1}, 64: {65: 1, 79: 1, 49: 8}, 65: {64: 1, 80: 1, 50: 4}, 67: {82: 1}, 68: {83: 1, 53: 4}, 70: {55: 1, 71: 1, 85: 1}, 71: {70: 1}, 72: {57: 1, 87: 1}, 73: {74: 1, 88: 1}, 74: {73: 1}, 75: {76: 1}, 76: {75: 1, 77: 1}, 77: {76: 1, 78: 1, 92: 1}, 78: {63: 1, 77: 1, 79: 1}, 79: {64: 1, 78: 1, 94: 1}, 80: {65: 1, 81: 8}, 81: {82: 1, 80: 8}, 82: {67: 1, 81: 1, 83: 1}, 83: {68: 1, 82: 1, 98: 1}, 85: {70: 1, 86: 8}, 86: {87: 1, 101: 1, 85: 8}, 87: {72: 1, 86: 1, 88: 4}, 88: {73: 1, 89: 1, 87: 4}, 89: {88: 1, 104: 1}, 90: {91: 1}, 91: {90: 1, 106: 1}, 92: {77: 1}, 93: {108: 1}, 94: {79: 1}, 97: {112: 1}, 98: {83: 1, 99: 1}, 99: {98: 1, 114: 1}, 100: {101: 1}, 101: {86: 1, 100: 1, 102: 1, 116: 1}, 102: {101: 1}, 103: {118: 1}, 104: {89: 1}, 106: {91: 1, 107: 1}, 107: {106: 1, 108: 1}, 108: {93: 1, 107: 1, 123: 1}, 112: {97: 1, 127: 1, 113: 7}, 113: {114: 1, 128: 1, 112: 7}, 114: {99: 1, 113: 1, 115: 1, 129: 1}, 115: {114: 1, 116: 1, 130: 8}, 116: {101: 1, 115: 1, 117: 1}, 117: {116: 1, 118: 1}, 118: {103: 1, 117: 1}, 120: {121: 1}, 121: {120: 1, 136: 1}, 122: {123: 1}, 123: {108: 1, 122: 1, 138: 1}, 126: {127: 1}, 127: {112: 1, 126: 1}, 128: {113: 1}, 129: {114: 1, 144: 4}, 130: {115: 8}, 135: {150: 1}, 136: {121: 1, 137: 1, 151: 1}, 137: {136: 1, 152: 1, 138: 9}, 138: {123: 1, 139: 5, 137: 9}, 139: {138: 5, 140: 8}, 140: {155: 1, 139: 8}, 141: {156: 1}, 142: {157: 8}, 143: {158: 1}, 144: {159: 8, 129: 4}, 149: {164: 1}, 150: {135: 1, 151: 1, 165: 1}, 151: {136: 1, 150: 1}, 152: {137: 1}, 153: {168: 1}, 154: {155: 1}, 155: {140: 1, 154: 1, 156: 1}, 156: {141: 1, 155: 1, 157: 1}, 157: {156: 1, 158: 1, 172: 1, 142: 8}, 158: {143: 1, 157: 1, 173: 1}, 159: {160: 1, 174: 1, 144: 8}, 160: {159: 1}, 163: {164: 5}, 164: {149: 1, 179: 1, 163: 5}, 165: {150: 1, 166: 1}, 166: {165: 1}, 167: {168: 9}, 168: {153: 1, 169: 1, 167: 9, 183: 8}, 169: {168: 1, 170: 1}, 170: {169: 1, 171: 8}, 171: {172: 1, 170: 8}, 172: {157: 1, 171: 1}, 173: {158: 1, 174: 4}, 174: {159: 1, 189: 1, 175: 4, 173: 4}, 175: {174: 4}, 177: {178: 1, 192: 1}, 178: {177: 1, 193: 1, 179: 7}, 179: {164: 1, 194: 1, 178: 7}, 180: {181: 1}, 181: {180: 1, 182: 1}, 182: {181: 1, 183: 1}, 183: {182: 1, 168: 8}, 184: {185: 1}, 185: {184: 1, 186: 7}, 186: {187: 1, 185: 7}, 187: {186: 1, 188: 5}, 188: {189: 1, 187: 5}, 189: {174: 1, 188: 1, 190: 1}, 190: {189: 1, 191: 1}, 191: {190: 1, 192: 1}, 192: {177: 1, 191: 1}, 193: {178: 1}, 194: {179: 1}}),
"start": 97},
"outputs": {"routing_table": {97: None, 112: 97, 127: 112, 126: 127, 113: 112, 114: 113, 128: 113, 99: 114, 115: 114, 129: 114, 98: 99, 116: 115, 83: 98, 101: 116, 117: 116, 68: 83, 82: 83, 86: 101, 100: 101, 102: 101, 118: 117, 67: 82, 81: 82, 87: 86, 103: 118, 144: 129, 72: 87, 57: 72, 53: 68, 58: 57, 38: 53, 52: 53, 59: 58, 88: 87, 130: 115, 23: 38, 37: 52, 44: 59, 73: 88, 89: 88, 8: 23, 22: 23, 29: 44, 74: 73, 104: 89, 9: 8, 85: 86, 10: 9, 70: 85, 80: 81, 159: 144, 55: 70, 65: 80, 71: 70, 160: 159, 174: 159, 28: 29, 56: 55, 64: 65, 189: 174, 41: 56, 79: 64, 188: 189, 190: 189, 14: 29, 40: 41, 78: 79, 94: 79, 191: 190, 50: 65, 63: 78, 77: 78, 173: 174, 175: 174, 192: 191, 21: 22, 62: 63, 76: 77, 92: 77, 158: 173, 177: 192, 6: 21, 36: 21, 75: 76, 143: 158, 157: 158, 178: 177, 7: 6, 35: 36, 156: 157, 172: 157, 187: 188, 193: 178, 34: 35, 141: 156, 155: 156, 171: 172, 186: 187, 47: 62, 49: 64, 140: 155, 154: 155, 46: 47, 48: 47, 26: 41, 45: 46, 61: 46, 11: 26, 25: 26, 30: 45, 60: 45, 12: 11, 15: 30, 179: 178, 0: 15, 13: 12, 16: 15, 142: 157, 164: 179, 194: 179, 31: 46, 149: 164, 185: 186, 170: 171, 184: 185, 139: 140, 169: 170, 168: 169, 32: 31, 153: 168, 163: 164, 1: 16, 138: 139, 123: 138, 108: 123, 122: 123, 93: 108, 107: 108, 106: 107, 183: 168, 91: 106, 167: 168, 182: 183, 90: 91, 181: 182, 180: 181, 137: 138, 136: 137, 152: 137, 121: 136, 151: 136, 120: 121, 150: 151, 135: 150, 165: 150, 166: 165},
"distances": {97: 0, 112: 1, 127: 2, 126: 3, 113: 8, 114: 9, 128: 9, 99: 10, 115: 10, 129: 10, 98: 11, 116: 11, 83: 12, 101: 12, 117: 12, 68: 13, 82: 13, 86: 13, 100: 13, 102: 13, 118: 13, 67: 14, 81: 14, 87: 14, 103: 14, 144: 14, 72: 15, 57: 16, 53: 17, 58: 17, 38: 18, 52: 18, 59: 18, 88: 18, 130: 18, 23: 19, 37: 19, 44: 19, 73: 19, 89: 19, 8: 20, 22: 20, 29: 20, 74: 20, 104: 20, 9: 21, 85: 21, 10: 22, 70: 22, 80: 22, 159: 22, 55: 23, 65: 23, 71: 23, 160: 23, 174: 23, 28: 24, 56: 24, 64: 24, 189: 24, 41: 25, 79: 25, 188: 25, 190: 25, 14: 26, 40: 26, 78: 26, 94: 26, 191: 26, 50: 27, 63: 27, 77: 27, 173: 27, 175: 27, 192: 27, 21: 28, 62: 28, 76: 28, 92: 28, 158: 28, 177: 28, 6: 29, 36: 29, 75: 29, 143: 29, 157: 29, 178: 29, 7: 30, 35: 30, 156: 30, 172: 30, 187: 30, 193: 30, 34: 31, 141: 31, 155: 31, 171: 31, 186: 31, 47: 32, 49: 32, 140: 32, 154: 32, 46: 33, 48: 33, 26: 34, 45: 34, 61: 34, 11: 35, 25: 35, 30: 35, 60: 35, 12: 36, 15: 36, 179: 36, 0: 37, 13: 37, 16: 37, 142: 37, 164: 37, 194: 37, 31: 38, 149: 38, 185: 38, 170: 39, 184: 39, 139: 40, 169: 40, 168: 41, 32: 42, 153: 42, 163: 42, 1: 45, 138: 45, 123: 46, 108: 47, 122: 47, 93: 48, 107: 48, 106: 49, 183: 49, 91: 50, 167: 50, 182: 50, 90: 51, 181: 51, 180: 52, 137: 54, 136: 55, 152: 55, 121: 56, 151: 56, 120: 57, 150: 57, 135: 58, 165: 58, 166: 59}}},
{"inputs": {"maze": MazeFromDict({0: {15: 1}, 1: {2: 4}, 2: {3: 1, 1: 4}, 3: {2: 1, 18: 1, 4: 4}, 4: {3: 4}, 5: {6: 5}, 6: {21: 1, 5: 5, 7: 9}, 7: {8: 1, 6: 9}, 8: {7: 1, 9: 1}, 9: {8: 1}, 10: {11: 1, 25: 1}, 11: {10: 1, 12: 1}, 12: {11: 1}, 13: {14: 1, 28: 1}, 14: {13: 1}, 15: {0: 1, 16: 1, 30: 1}, 16: {15: 1}, 18: {3: 1, 19: 1, 33: 4}, 19: {18: 1, 34: 1, 20: 8}, 20: {21: 1, 19: 8}, 21: {6: 1, 20: 1, 22: 1}, 22: {21: 1, 23: 1, 37: 1}, 23: {22: 1, 24: 1}, 24: {23: 1, 25: 1}, 25: {10: 1, 24: 1, 26: 7}, 26: {27: 1, 25: 7}, 27: {26: 1, 28: 1}, 28: {13: 1, 27: 1, 29: 1}, 29: {28: 1, 44: 9}, 30: {15: 1, 31: 1, 45: 1}, 31: {30: 1, 46: 1, 32: 7}, 32: {33: 1, 47: 1, 31: 7}, 33: {32: 1, 18: 4}, 34: {19: 1}, 37: {22: 1, 52: 1}, 43: {44: 1, 58: 1}, 44: {43: 1, 59: 1, 29: 9}, 45: {30: 1, 60: 1}, 46: {31: 1, 61: 8}, 47: {32: 1}, 51: {52: 1, 66: 1}, 52: {37: 1, 51: 1, 53: 9}, 53: {52: 9}, 58: {43: 1, 73: 1}, 59: {44: 1, 74: 5}, 60: {45: 1, 75: 1}, 61: {46: 8}, 64: {65: 1, 79: 1}, 65: {64: 1, 80: 1}, 66: {51: 1, 81: 1}, 69: {84: 1}, 72: {73: 1}, 73: {58: 1, 72: 1}, 74: {89: 1, 59: 5}, 75: {60: 1, 90: 9}, 79: {64: 1}, 80: {65: 1, 95: 1, 81: 9}, 81: {66: 1, 96: 6, 80: 9}, 82: {97: 1}, 83: {98: 1}, 84: {69: 1, 99: 1}, 87: {88: 1}, 88: {87: 1, 89: 1}, 89: {74: 1, 88: 1, 104: 1}, 90: {105: 1, 75: 9}, 93: {94: 1}, 94: {93: 1, 95: 1}, 95: {80: 1, 94: 1}, 96: {111: 1, 81: 6}, 97: {82: 1, 98: 1, 112: 1}, 98: {83: 1, 97: 1, 99: 1}, 99: {84: 1, 98: 1}, 102: {117: 1}, 103: {118: 1}, 104: {89: 1, 119: 1}, 105: {90: 1, 106: 1}, 106: {105: 1, 121: 5}, 107: {108: 1}, 108: {107: 1, 123: 1}, 109: {110: 1}, 110: {109: 1, 111: 1, 125: 1}, 111: {96: 1, 110: 1, 112: 1, 126: 1}, 112: {97: 1, 111: 1, 113: 1}, 113: {112: 1, 114: 1, 128: 1}, 114: {113: 1, 115: 1, 129: 1}, 115: {114: 1, 130: 1, 116: 5}, 116: {117: 1, 131: 1, 115: 5}, 117: {102: 1, 116: 1, 118: 1, 132: 1}, 118: {103: 1, 117: 1}, 119: {104: 1}, 121: {136: 1, 106: 5}, 122: {137: 1}, 123: {108: 1, 124: 1}, 124: {123: 1, 125: 8}, 125: {110: 1, 124: 8}, 126: {111: 1, 127: 1, 141: 1}, 127: {126: 1}, 128: {113: 1, 143: 1}, 129: {114: 1}, 130: {115: 1}, 131: {116: 1, 146: 1}, 132: {117: 1, 133: 5}, 133: {134: 1, 132: 5}, 134: {133: 1, 149: 1}, 136: {121: 1}, 137: {122: 1, 152: 1}, 138: {139: 6}, 139: {140: 1, 138: 6}, 140: {139: 1, 141: 1, 155: 1}, 141: {126: 1, 140: 1, 142: 5}, 142: {157: 1, 141: 5}, 143: {128: 1, 158: 1}, 145: {146: 1}, 146: {131: 1, 145: 1, 147: 1, 161: 1}, 147: {146: 1, 148: 1, 162: 1}, 148: {147: 1, 163: 1}, 149: {134: 1}, 151: {152: 1}, 152: {137: 1, 151: 1, 153: 1}, 153: {152: 1, 154: 1}, 154: {153: 1, 169: 1}, 155: {140: 1, 156: 1, 170: 1}, 156: {155: 1, 171: 1}, 157: {142: 1}, 158: {143: 1}, 161: {146: 1}, 162: {147: 1}, 163: {148: 1, 164: 1, 178: 8}, 164: {163: 1, 179: 1}, 168: {169: 1, 183: 9}, 169: {154: 1, 168: 1, 184: 1, 170: 5}, 170: {155: 1, 185: 1, 169: 5}, 171: {156: 1, 172: 1}, 172: {171: 1, 173: 1}, 173: {172: 1, 188: 4, 174: 9}, 174: {173: 9, 175: 5}, 175: {176: 1, 190: 6, 174: 5}, 176: {175: 1, 177: 1, 191: 1}, 177: {176: 1, 192: 1}, 178: {163: 8}, 179: {164: 1}, 180: {181: 1}, 183: {182: 1, 168: 9}, 184: {169: 1}, 185: {170: 1, 186: 4}, 186: {187: 1, 185: 4}, 187: {186: 1}, 188: {189: 1, 173: 4}, 189: {188: 1}, 190: {175: 6}, 191: {176: 1}, 192: {177: 1, 193: 4}, 193: {192: 4, 194: 6}, 194: {193: 6}, 182: {183: 1, 181: 1}, 181: {180: 1, 182: 1}}),
"start": 97},
"outputs": {"routing_table": {97: None, 82: 97, 98: 97, 112: 97, 83: 98, 99: 98, 111: 112, 113: 112, 84: 99, 96: 111, 110: 111, 114: 113, 126: 111, 128: 113, 69: 84, 109: 110, 115: 114, 125: 110, 127: 126, 129: 114, 141: 126, 143: 128, 130: 115, 140: 141, 158: 143, 139: 140, 155: 140, 156: 155, 170: 155, 171: 156, 185: 170, 81: 96, 116: 115, 142: 141, 172: 171, 66: 81, 117: 116, 131: 116, 157: 142, 173: 172, 51: 66, 102: 117, 118: 117, 132: 117, 146: 131, 52: 51, 103: 118, 124: 125, 138: 139, 145: 146, 147: 146, 161: 146, 169: 170, 186: 185, 37: 52, 123: 124, 148: 147, 154: 169, 162: 147, 168: 169, 184: 169, 187: 186, 22: 37, 108: 123, 153: 154, 163: 148, 188: 173, 21: 22, 23: 22, 107: 108, 152: 153, 164: 163, 189: 188, 6: 21, 20: 21, 24: 23, 133: 132, 137: 152, 151: 152, 179: 164, 25: 24, 122: 137, 134: 133, 10: 25, 80: 81, 149: 134, 11: 10, 65: 80, 95: 80, 174: 173, 12: 11, 64: 65, 94: 95, 5: 6, 53: 52, 79: 64, 93: 94, 178: 163, 183: 168, 182: 183, 19: 20, 26: 25, 175: 174, 181: 182, 7: 6, 18: 19, 27: 26, 34: 19, 176: 175, 180: 181, 3: 18, 8: 7, 28: 27, 177: 176, 191: 176, 2: 3, 9: 8, 13: 28, 29: 28, 192: 177, 14: 13, 33: 18, 4: 3, 32: 33, 190: 175, 1: 2, 47: 32, 193: 192, 44: 29, 31: 32, 43: 44, 59: 44, 194: 193, 30: 31, 46: 31, 58: 43, 15: 30, 45: 30, 73: 58, 0: 15, 16: 15, 60: 45, 72: 73, 75: 60, 74: 59, 89: 74, 88: 89, 104: 89, 87: 88, 119: 104, 61: 46, 90: 75, 105: 90, 106: 105, 121: 106, 136: 121},
"distances": {97: 0, 82: 1, 98: 1, 112: 1, 83: 2, 99: 2, 111: 2, 113: 2, 84: 3, 96: 3, 110: 3, 114: 3, 126: 3, 128: 3, 69: 4, 109: 4, 115: 4, 125: 4, 127: 4, 129: 4, 141: 4, 143: 4, 130: 5, 140: 5, 158: 5, 139: 6, 155: 6, 156: 7, 170: 7, 171: 8, 185: 8, 81: 9, 116: 9, 142: 9, 172: 9, 66: 10, 117: 10, 131: 10, 157: 10, 173: 10, 51: 11, 102: 11, 118: 11, 132: 11, 146: 11, 52: 12, 103: 12, 124: 12, 138: 12, 145: 12, 147: 12, 161: 12, 169: 12, 186: 12, 37: 13, 123: 13, 148: 13, 154: 13, 162: 13, 168: 13, 184: 13, 187: 13, 22: 14, 108: 14, 153: 14, 163: 14, 188: 14, 21: 15, 23: 15, 107: 15, 152: 15, 164: 15, 189: 15, 6: 16, 20: 16, 24: 16, 133: 16, 137: 16, 151: 16, 179: 16, 25: 17, 122: 17, 134: 17, 10: 18, 80: 18, 149: 18, 11: 19, 65: 19, 95: 19, 174: 19, 12: 20, 64: 20, 94: 20, 5: 21, 53: 21, 79: 21, 93: 21, 178: 22, 183: 22, 182: 23, 19: 24, 26: 24, 175: 24, 181: 24, 7: 25, 18: 25, 27: 25, 34: 25, 176: 25, 180: 25, 3: 26, 8: 26, 28: 26, 177: 26, 191: 26, 2: 27, 9: 27, 13: 27, 29: 27, 192: 27, 14: 28, 33: 29, 4: 30, 32: 30, 190: 30, 1: 31, 47: 31, 193: 31, 44: 36, 31: 37, 43: 37, 59: 37, 194: 37, 30: 38, 46: 38, 58: 38, 15: 39, 45: 39, 73: 39, 0: 40, 16: 40, 60: 40, 72: 40, 75: 41, 74: 42, 89: 43, 88: 44, 104: 44, 87: 45, 119: 45, 61: 46, 90: 50, 105: 51, 106: 52, 121: 57, 136: 58}}}]
# Test on several controlled examples
for i in range(len(TESTS)):
# Instantiate the player
player = Dijkstra()
# Get the input and output data
maze = TESTS[i]["inputs"]["maze"]
start = TESTS[i]["inputs"]["start"]
target_routing_table = TESTS[i]["outputs"]["routing_table"]
target_distances = TESTS[i]["outputs"]["distances"]
# Perform the traversal
distances, routing_table = player.traversal(maze, start)
# Check that outputs match the expected ones
self.assertEqual(sorted(routing_table), sorted(target_routing_table))
self.assertEqual(sorted(distances), sorted(target_distances))
##################################################################################
def test_find_route (self) -> None:
"""
This method tests the ``find_route(...)`` method.
Here, we want to make sure that the output corresponds indeed to a route from the start to the end.
We are going to check the following:
- Outputs are of the expected types.
- The route is a valid path from the start to the end.
The method will be tested on some controlled examples, where we can easily check the validity of the output.
"""
# Constants
INPUTS = [{"routing_table": {0: None, 1: 0, 2: 1, 3: 2, 4: 3},
"start": 0,
"end": 4},
{"routing_table": {0: 2, 1: None, 2: 1, 3: 0, 4: 0, 5: 4, 6: 1},
"start": 1,
"end": 6}]
# Test on several controlled examples
for i in range(len(INPUTS)):
# Instantiate the player
player = Dijkstra()
# Get the input data
routing_table = INPUTS[i]["routing_table"]
start = INPUTS[i]["start"]
end = INPUTS[i]["end"]
# Find the route
route = player.find_route(routing_table, start, end)
# Check the output type
# It should be a list of integers
self.assertTrue(isinstance(route, list))
self.assertTrue(all(isinstance(v, int) for v in route))
# Check that the route is a valid path from the start to the end
self.assertEqual(route[0], start)
self.assertEqual(route[-1], end)
self.assertTrue(all(routing_table[route[j + 1]] == route[j] for j in range(len(route) - 1)))
##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################
if __name__ == "__main__":
# Run all tests
unittest.main(verbosity=2)
##########################################################################################
##########################################################################################La vidéo suivante montre un exemple de ce que vous devriez observer :
Notez que le rat a volontairement évité de la boue car le nombre de tours nécessaires pour l’esquiver est inférieur au nombre de tours nécessaires pour la traverser.
Pour aller plus loin
2 — Comparer avec les autres parcours
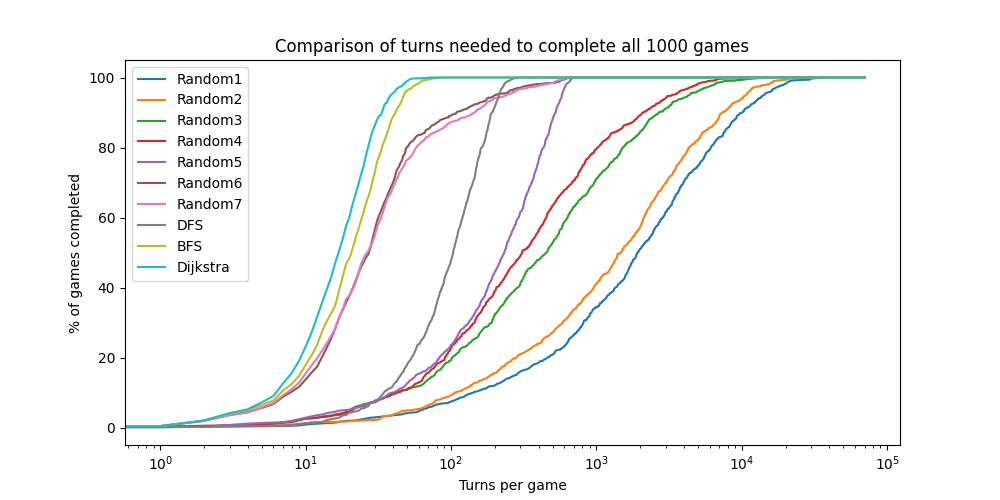
Comme précédemment, une chose simple que vous pouvez faire maintenant est de comparer tous les joueurs RandomX.py, DFS.py, BFS.py et Dijkstra.py sur des graphes pondérés.
Adaptez le script evaluate_random_players.py (ou le nom que vous lui avez donné) des séances précédentes pour comparer le nombre moyen de tours nécessaires pour chaque joueur pour finir toutes les parties.
Qu’observez-vous ?
Le script modifié devrait ressembler à ça :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import tqdm.auto as tqdm
import matplotlib.pyplot as pyplot
import scipy.stats as scstats
# PyRat imports
from pyrat import Game, GameMode
from players.Random1 import Random1
from players.Random2 import Random2
from players.Random3 import Random3
from players.Random4 import Random4
from players.Random5 import Random5
from players.Random6 import Random6
from players.Random7 import Random7
from players.DFS import DFS
from players.BFS import BFS
from players.Dijkstra import Dijkstra
##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################
if __name__ == "__main__":
# Determines how many games will be played for each player
nb_games = 1000
# Customize the game elements
game_config = {"mud_percentage": 30.0,
"nb_cheese": 1,
"game_mode": GameMode.SIMULATION}
# Run the games for each player class
players = [Random1(), Random2(), Random3(), Random4(), Random5(), Random6(), Random7(), DFS(), BFS(), Dijkstra()]
results = {player.get_name(): [] for player in players}
for player in players:
for seed in tqdm.tqdm(range(nb_games), desc=player.get_name()):
# Make the game with given seed
game = Game(random_seed=seed, **game_config)
game.add_player(player)
stats = game.start()
# Store the number of turns needed
results[player.get_name()].append(stats["turns"])
# Visualization of cumulative curves of numbers of turns taken per program
max_turn = max([max(results[player]) for player in results])
pyplot.figure(figsize=(10, 5))
for player in results:
turns = [0] + sorted(results[player]) + [max_turn]
games_completed_per_turn = [len([turn for turn in results[player] if turn <= t]) * 100.0 / nb_games for t in turns]
pyplot.plot(turns, games_completed_per_turn, label=player)
pyplot.title("Comparison of turns needed to complete all %d games" % (nb_games))
pyplot.xlabel("Turns per game")
pyplot.ylabel("% of games completed")
pyplot.xscale("log")
pyplot.legend()
pyplot.savefig("evaluate_random_vs_traversals_weighted.png")
# Formal statistics to check if these curves are statistically significant
for i, player_1 in enumerate(results):
for j, player_2 in enumerate(results):
if j > i:
test_result = scstats.mannwhitneyu(results[player_1], results[player_2], alternative="two-sided")
print("Mann-Whitney U test between turns of program '%s' and of program '%s':" % (player_1, player_2), test_result)
##########################################################################################
##########################################################################################Et son exécution produira des résultats similaires à ceux-ci :
Mann-Whitney U test between turns of program 'Random1' and of program 'Random2':
MannwhitneyuResult(statistic=np.float64(558361.5), pvalue=np.float64(6.198732319934707e-06))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random3':
MannwhitneyuResult(statistic=np.float64(739525.5), pvalue=np.float64(8.323664416534917e-77))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(780667.5), pvalue=np.float64(9.588021797027599e-105))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(870070.0), pvalue=np.float64(1.2625727667270109e-180))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(964132.5), pvalue=np.float64(6.431479339414483e-283))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(962014.5), pvalue=np.float64(2.319712695688142e-280))
Mann-Whitney U test between turns of program 'Random1' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(923721.5), pvalue=np.float64(3.818947795022368e-236))
Mann-Whitney U test between turns of program 'Random1' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(979797.0), pvalue=np.float64(3.342524319849158e-302))
Mann-Whitney U test between turns of program 'Random1' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(983373.5), pvalue=np.float64(1.051718106040382e-306))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random3':
MannwhitneyuResult(statistic=np.float64(690770.5), pvalue=np.float64(2.177872139639425e-49))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(736415.0), pvalue=np.float64(7.1412267680911125e-75))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(832986.0), pvalue=np.float64(1.2558377249870235e-146))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(958815.0), pvalue=np.float64(1.6023373517426064e-276))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(955738.0), pvalue=np.float64(7.467004200902423e-273))
Mann-Whitney U test between turns of program 'Random2' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(906369.5), pvalue=np.float64(2.2748146093543353e-217))
Mann-Whitney U test between turns of program 'Random2' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(979405.5), pvalue=np.float64(1.033204905303594e-301))
Mann-Whitney U test between turns of program 'Random2' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(982899.5), pvalue=np.float64(4.1670235161978846e-306))
Mann-Whitney U test between turns of program 'Random3' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(554438.5), pvalue=np.float64(2.4900178747477667e-05))
Mann-Whitney U test between turns of program 'Random3' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(665399.0), pvalue=np.float64(1.4688160797004256e-37))
Mann-Whitney U test between turns of program 'Random3' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(906118.0), pvalue=np.float64(4.098175981577282e-217))
Mann-Whitney U test between turns of program 'Random3' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(900565.0), pvalue=np.float64(2.838489841229785e-211))
Mann-Whitney U test between turns of program 'Random3' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(803571.0), pvalue=np.float64(3.3223614670070864e-122))
Mann-Whitney U test between turns of program 'Random3' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(946114.5), pvalue=np.float64(1.4712162288754023e-261))
Mann-Whitney U test between turns of program 'Random3' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(955613.5), pvalue=np.float64(9.787564101128113e-273))
Mann-Whitney U test between turns of program 'Random4' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(605786.0), pvalue=np.float64(2.5675179048571897e-16))
Mann-Whitney U test between turns of program 'Random4' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(898203.0), pvalue=np.float64(8.16373047459855e-209))
Mann-Whitney U test between turns of program 'Random4' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(890944.5), pvalue=np.float64(2.3995944792444313e-201))
Mann-Whitney U test between turns of program 'Random4' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(770421.0), pvalue=np.float64(2.2395139668021272e-97))
Mann-Whitney U test between turns of program 'Random4' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(946369.5), pvalue=np.float64(7.43518858223359e-262))
Mann-Whitney U test between turns of program 'Random4' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(956168.0), pvalue=np.float64(2.147803847384719e-273))
Mann-Whitney U test between turns of program 'Random5' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(883250.0), pvalue=np.float64(1.3987525709838941e-193))
Mann-Whitney U test between turns of program 'Random5' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(874029.5), pvalue=np.float64(1.7791654670438421e-184))
Mann-Whitney U test between turns of program 'Random5' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(749239.5), pvalue=np.float64(5.240039083860192e-83))
Mann-Whitney U test between turns of program 'Random5' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(941620.5), pvalue=np.float64(2.3340261693475594e-256))
Mann-Whitney U test between turns of program 'Random5' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(951831.0), pvalue=np.float64(2.9164469015990905e-268))
Mann-Whitney U test between turns of program 'Random6' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(494559.5), pvalue=np.float64(0.6735091055062531))
Mann-Whitney U test between turns of program 'Random6' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(162119.5), pvalue=np.float64(6.405872673441549e-151))
Mann-Whitney U test between turns of program 'Random6' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(606551.5), pvalue=np.float64(1.5421531819900166e-16))
Mann-Whitney U test between turns of program 'Random6' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(677083.0), pvalue=np.float64(8.029647822629658e-43))
Mann-Whitney U test between turns of program 'Random7' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(180358.0), pvalue=np.float64(2.811573603890319e-135))
Mann-Whitney U test between turns of program 'Random7' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(607811.0), pvalue=np.float64(6.785926054128128e-17))
Mann-Whitney U test between turns of program 'Random7' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(673921.0), pvalue=np.float64(2.285251193703512e-41))
Mann-Whitney U test between turns of program 'DFS' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(942846.0), pvalue=np.float64(8.965401864417458e-258))
Mann-Whitney U test between turns of program 'DFS' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(959817.0), pvalue=np.float64(9.410337210363598e-278))
Mann-Whitney U test between turns of program 'BFS' and of program 'Dijkstra':
MannwhitneyuResult(statistic=np.float64(585881.0), pvalue=np.float64(2.8689460106101822e-11))On peut observer que le BFS ne trouve en effet plus le chemin le plus rapide dans un labyrinthe avec de la boue, contrairement à l’algorithme de Dijkstra. Cela se traduit par un nombre moyen de tours plus élevé pour le BFS par rapport à Dijkstra. Ces résultats sont statistiquement significatifs, comme l’indique la p-value très faible du test de Mann-Whitney entre les deux algorithmes.
Ça pourrait être intéressant de faire varier le pourcentage de boue dans le labyrinthe et d’observer comment cela affecte les performances relatives des deux algorithmes. On se doute que plus il y a de boue, plus la différence de performance entre BFS et Dijkstra sera marquée.
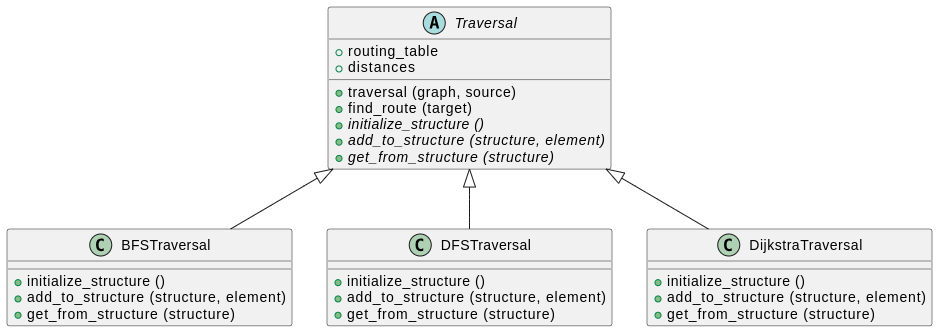
3 — Factoriser les codes
Si vous avez suivi la partie optionnelle de la session précédente, vous devriez avoir factorisé vos fichiers BFS.py et DFS.py dans une classe Traversal à partir de laquelle vous dérivez deux classes BFSTraversal et DFSTraversal.
Avec quelques adaptations possibles dans Traversal.py, créez une classe DijkstraTraversal qui hérite de Traversal.
Adaptez également l’énumération et le constructeur dans TraversalPlayer.py pour ajouter l’option d’utiliser l’algorithme de Dijkstra.
Le fichier Traversal.py donné en correction de la séance précédente est déjà prêt pour l’ajout de Dijkstra.
Il suffit de bien faire attention à mettre la longueur du chemin comme premier élément du tuple représentant les sommets dans la file de priorité.
Pour la classe DijkstraTraversal, le code ressemblera à ça :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import heapq
# PyRat imports
from utils.Traversal import Traversal
##########################################################################################
######################################### CLASSES ########################################
##########################################################################################
class DijkstraTraversal (Traversal):
"""
This class implements Dijkstra's traversal algorithm by defining the abstract methods from the parent class.
We use a priority queue to indicate the order in which vertices should be explored.
"""
##################################################################################
# CONSTRUCTOR #
##################################################################################
def __init__ ( self,
*args: object,
**kwargs: object
) -> None:
"""
*(This class inherits from* ``Traversal`` *).*
It implements Dijkstra's traversal algorithm by defining the abstract methods from the parent class.
We use a priority queue to indicate the order in which vertices should be explored.
Args:
args: Arguments to pass to the parent constructor.
kwargs: Keyword arguments to pass to the parent constructor.
"""
# Inherit from parent class
super().__init__(*args, **kwargs)
##################################################################################
# METHODS #
##################################################################################
def initialize_structure (self) -> object:
"""
*(This method redefines the method of the parent class with the same name).*
It initializes the data structure needed for the traversal.
Here, we use a priority queue.
Returns:
The initialized data structure.
"""
# We return an empty list
return []
##################################################################################
def add_to_structure ( self,
structure: object,
element: object
) -> object:
"""
*(This method redefines the method of the parent class with the same name).*
It adds an element to the data structure and returns the updated data structure.
Here, we add the element to the priority queue using `heapq.heappush`.
Returns:
The updated data structure.
"""
# We append the element to the structure
heapq.heappush(structure, element)
return structure
##################################################################################
def get_from_structure ( self,
structure: object,
) -> tuple[object, object]:
"""
*(This method is abstract and must be implemented in the subclasses).*
It extracts an element from the data structure and returns it along with the updated data structure.
Here, we remove and return the element with the highest priority using `heapq.heappop`.
Returns:
A tuple containing the extracted element and the updated data structure.
"""
# We remove and return the first element of the list
element = heapq.heappop(structure)
return element, structure
##########################################################################################
##########################################################################################Et on peut adapter l’énumération et le constructeur dans TraversalPlayer.py comme suit :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import enum
# PyRat imports
from pyrat import Player, Maze, GameState, Action
from utils.BFSTraversal import BFSTraversal
from utils.DFSTraversal import DFSTraversal
from utils.DijkstraTraversal import DijkstraTraversal
##########################################################################################
######################################### CLASSES ########################################
##########################################################################################
class TraversalAlgorithm (enum.Enum):
"""
This enumeration defines all the possible algorithms handled by the ``TraversalPlayer``.
Possible algorithms are:
* ``BFS``: Breadth-first search.
* ``DFS``: Depth-first search.
* ``DIJKSTRA``: Dijkstra's algorithm.
"""
BFS = "bfs"
DFS = "dfs"
DIJKSTRA = "dijkstra"
##########################################################################################
class TraversalPlayer (Player):
"""
*(This class inherits from* ``Player`` *).*
This player controls a PyRat character that explores the maze using a graph traversal algorithm.
The algorithm can be chosen among those defined in the ``TraversalAlgorithm`` enumeration.
"""
##################################################################################
# CONSTRUCTOR #
##################################################################################
def __init__ ( self,
algorithm: TraversalAlgorithm,
enable_early_stop: bool = True,
*args: object,
**kwargs: object
) -> None:
"""
Initializes a new instance of the class.
Here, the constructor is only used to initialize the player.
It transmits the arguments to the parent constructor, which is responsible for initializing the name and the skin of the player.
Args:
algorithm: The traversal algorithm to use, among those defined in the ``TraversalAlgorithm`` enumeration.
enable_early_stop: Whether to stop the traversal as soon as a piece of cheese is found (``True``) or to traverse the whole maze (``False``).
args: Arguments to pass to the parent constructor.
kwargs: Keyword arguments to pass to the parent constructor.
"""
# Inherit from parent class
super().__init__(*args, **kwargs)
# Debug
assert isinstance(algorithm, TraversalAlgorithm), "The algorithm must be an instance of the TraversalAlgorithm enumeration"
# We create an attribute to store the actions to perform
self.actions = None
# We initialize the chosen traversal algorithm
self.enable_early_stop = enable_early_stop
self.traversal_algorithm = None
if algorithm == TraversalAlgorithm.BFS:
self.traversal_algorithm = BFSTraversal()
elif algorithm == TraversalAlgorithm.DFS:
self.traversal_algorithm = DFSTraversal()
elif algorithm == TraversalAlgorithm.DIJKSTRA:
self.traversal_algorithm = DijkstraTraversal()
##################################################################################
# PYRAT METHODS #
##################################################################################
def preprocessing ( self,
maze: Maze,
game_state: GameState,
) -> None:
"""
*(This method redefines the method of the parent class with the same name).*
This method is called once at the beginning of the game.
Here, we use the traversal algorithm to compute a shortest path that reaches the piece of cheese from the initial position of the player.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
"""
# Depending on whether early stopping is enabled, we set the stop vertices to the cheese locations or to an empty set
if self.enable_early_stop:
early_stop_vertices = game_state.cheese
else:
early_stop_vertices = set()
# We perform a traversal of the maze graph from the initial position of the player
my_location = game_state.player_locations[self.get_name()]
self.traversal_algorithm.traversal(maze, my_location, early_stop_vertices)
print(f"Stop vertex found: {self.traversal_algorithm.stop_vertex_found}")
# Find the series of locations/actions to go from the player location to the first piece of cheese
path = self.traversal_algorithm.find_route(game_state.cheese[0])
self.actions = maze.locations_to_actions(path)
##################################################################################
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
"""
*(This method redefines the method of the parent class with the same name).*
It is called at each turn of the game.
It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
Returns:
One of the possible actions.
"""
# At each turn, we perform the next action in the list of actions
return self.actions.pop(0)
##########################################################################################
##########################################################################################Voici le diagramme UML de la séance 2, auquel nous avons ajouté cette nouvelle classe :
Pour aller encore plus loin
4 — L’algorithme de Floyd-Warshall
L’algorithme de Dijkstra est ce que nous appelons un algorithme “1-to-*”. Cela signifie qu’il trouvera les chemins les plus courts d’une position initiale unique à toutes les autres positions du graphe.
L’algorithme de Floyd-Warshall est ce que nous appelons un algorithme “*-to-*”. Il calculera simultanément tous les chemins les plus courts de tous les sommets à tous les sommets.
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
Soit $n$ le nombre de sommets dans le graphe (cases du labyrinthe).
Dans un labyrinthe PyRat, l’algorithme de Dijkstra a une complexité de $O(n \cdot log(n))$. Par conséquent, si nous l’exécutons depuis chaque position possible ($n$ fois), nous obtenons une complexité de $O(n^2 \cdot log(n))$.
Comme l’algorithme de Floyd-Warshall a une complexité de $O(n^3)$, utiliser plusieurs fois l’algorithme de Dijkstra est préférable.
Essayez d’implémenter cet algorithme (ou peut-être trouvez une bibliothèque qui le fait ?).
Voici un joueur possible utilisant l’algorithme de Floyd-Warshall :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import heapq
# PyRat imports
from pyrat import Player, Maze, GameState, Action, Graph
##########################################################################################
######################################### CLASSES ########################################
##########################################################################################
class FloydWarshall (Player):
"""
*(This class inherits from* ``Player`` *).*
This player performs Floyd-Warshall's algorithm to find the shortest paths in the maze.
Computation of the paths is done in the ``preprocessing(...)`` method.
The path from the initial location to the cheese is then followed in the ``turn(...)`` method.
"""
##################################################################################
# CONSTRUCTOR #
##################################################################################
def __init__ ( self,
*args: object,
**kwargs: object
) -> None:
"""
Initializes a new instance of the class.
Args:
args: Arguments to pass to the parent constructor.
kwargs: Keyword arguments to pass to the parent constructor.
"""
# Inherit from parent class
super().__init__(*args, **kwargs)
# We create an attribute to store the actions to perform
self.actions = None
##################################################################################
# PYRAT METHODS #
##################################################################################
def preprocessing ( self,
maze: Maze,
game_state: GameState,
) -> None:
"""
*(This method redefines the method of the parent class with the same name).*
This method is called once at the beginning of the game.
Here, we use Floyd-Warshall's algorithm to compute the shortest paths between all pairs of vertices.
From this, we extract the path from the initial location of the player to the first piece of cheese.
The actions corresponding to the path are stored in the ``actions`` attribute, and will be used in the ``turn(...)`` method.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
"""
# We perform a traversal of the maze graph
distances, routing_tables = self.traversal(maze)
# Find the series of locations/actions to go from the player location to the first piece of cheese
my_location = game_state.player_locations[self.get_name()]
routing_table = routing_tables[my_location]
path = self.find_route(routing_table, my_location, game_state.cheese[0])
self.actions = maze.locations_to_actions(path)
##################################################################################
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
"""
*(This method redefines the method of the parent class with the same name).*
It is called at each turn of the game.
It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
The action is chosen by following the path computed in the ``preprocessing(...)`` method.
Args:
maze: An object representing the maze in which the player plays.
game_state: An object representing the state of the game.
Returns:
One of the possible actions.
"""
# At each turn, we perform the next action in the list of actions
return self.actions.pop(0)
##################################################################################
# OTHER METHODS #
##################################################################################
def traversal ( self,
graph: Graph,
) -> tuple[dict[int, dict[int, int]], dict[int, dict[int, int | None]]]:
"""
This method performs Floyd-Warshall's algorithm on a graph.
It returns distances between vertices.
It also returns the routing table for each vertex.
Args:
graph: The graph to traverse.
Returns:
A tuple containing:
- The distances from each vertex to each explored vertex.
- For each vertex, the routing table from this vertex, that is, the parent of each vertex in the traversal (None for the source).
"""
# Initialization
vertices = list(graph.get_vertices())
distances = {u: {v: float('inf') for v in vertices} for u in vertices}
routing_tables = {u: {v: None for v in vertices} for u in vertices}
# Distance to itself
for u in vertices:
distances[u][u] = 0
# Direct edges
for u in vertices:
for v in graph.get_neighbors(u):
w = graph.get_weight(u, v)
distances[u][v] = w
routing_tables[u][v] = u
# Floyd-Warshall
for k in vertices:
for i in vertices:
for j in vertices:
dist_through_k = distances[i][k] + distances[k][j]
if dist_through_k < distances[i][j]:
distances[i][j] = dist_through_k
routing_tables[i][j] = routing_tables[k][j]
# Return the result
return distances, routing_tables
##################################################################################
def find_route ( self,
routing_table: dict[int, int | None],
source: int,
target: int
) -> list[int]:
"""
This method finds the route from a source vertex to a target vertex using a routing table.
Args:
routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
source: The source vertex.
target: The target vertex.
Returns:
The route from the source to the target as a list of vertices.
"""
# Initialization
route = [target]
vertex = target
# Find the route
while vertex != source:
vertex = routing_table[vertex]
route.append(vertex)
# Reverse the route
route.reverse()
return route
##########################################################################################
##########################################################################################Et un script de jeu pour le visualiser :
##########################################################################################
########################################## INFO ##########################################
##########################################################################################
"""
This program is a solution to the practical session 3 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session3/practical/
"""
##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################
# External imports
import pprint
# PyRat imports
from pyrat import Game
from players.FloydWarshall import FloydWarshall
##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################
if __name__ == "__main__":
# Instantiate a game with a few arguments
game_config = {"mud_percentage": 20.0,
"maze_width": 13,
"maze_height": 10,
"nb_cheese": 1,
"random_seed": 42,
"trace_length": 1000}
# Instantiate a game with specified arguments
game = Game(**game_config)
# Instantiate the player
player = FloydWarshall()
game.add_player(player)
# Start the game
stats = game.start()
pprint.pprint(stats)
##########################################################################################
##########################################################################################5 — L’algorithme de Bellman-Ford
L’algorithme de Bellman-Ford est également un algorithme “1-to-*”. Cependant, contrairement à l’algorithme de Dijkstra, il a la propriété de pouvoir trouver le chemin le plus court si certains arcs ont des poids négatifs. De plus, il peut être utilisé pour détecter un cycle absorbant dans le graphe.
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
L’algorithme de Bellman-Ford a une complexité de $O(mn)$, avec $n$ le nombre de sommets dans le graphe et $m$ le nombre d’arcs dans le graphe. Dans le cas d’un jeu PyRat, chaque sommet a au plus 4 voisins. Par conséquent, dans ce cas particulier, l’algorithme de Bellman-Ford a une complexité de $O(4n \cdot n)$, ou $O(n^2)$.
Comme nous n’avons pas de poids négatifs dans un labyrinthe PyRat (ce qui justifierait le choix de l’algorithme de Bellman-Ford), l’algorithme de Dijkstra est préférable.
Essayez d’implémenter cet algorithme (ou peut-être trouvez une bibliothèque qui le fait ?).
6 — L’algorithme de Johnson
L’algorithme de Johnson est un algorithme “*-to-*”, qui exploite l’algorithme de Bellman-Ford pour trouver tous les chemins les plus courts dans le graphe.
Lisez un peu sur cet algorithme. Devriez-vous l’utiliser dans le projet ?
L’algorithme de Johnson a une complexité de $O(n^2 \cdot log(n) + mn)$, avec $n$ le nombre de sommets dans le graphe et $m$ le nombre d’arcs dans le graphe.
Comparé à la complexité de Dijkstra de $O(n^2 \cdot log(n))$, et comme nous n’avons pas de poids négatifs dans un labyrinthe PyRat (ce qui justifierait le choix de l’algorithme de Johnson), plusieurs appels à l’algorithme de Dijkstra sont préférables.
Essayez d’implémenter cet algorithme (ou peut-être trouvez une bibliothèque qui le fait ?).