Complexité des problèmes & NP-complétude

En bref

Résumé de l’article

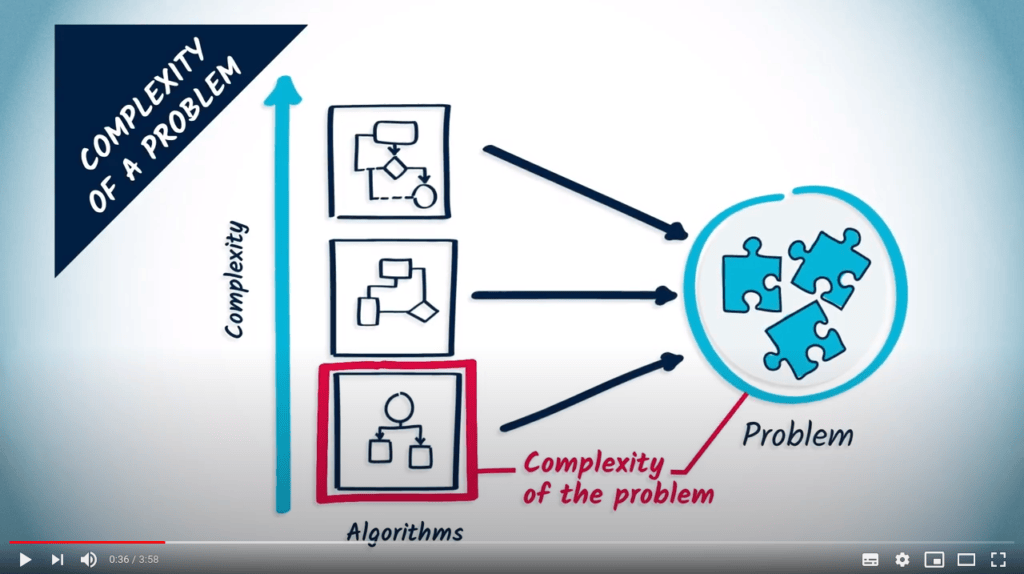
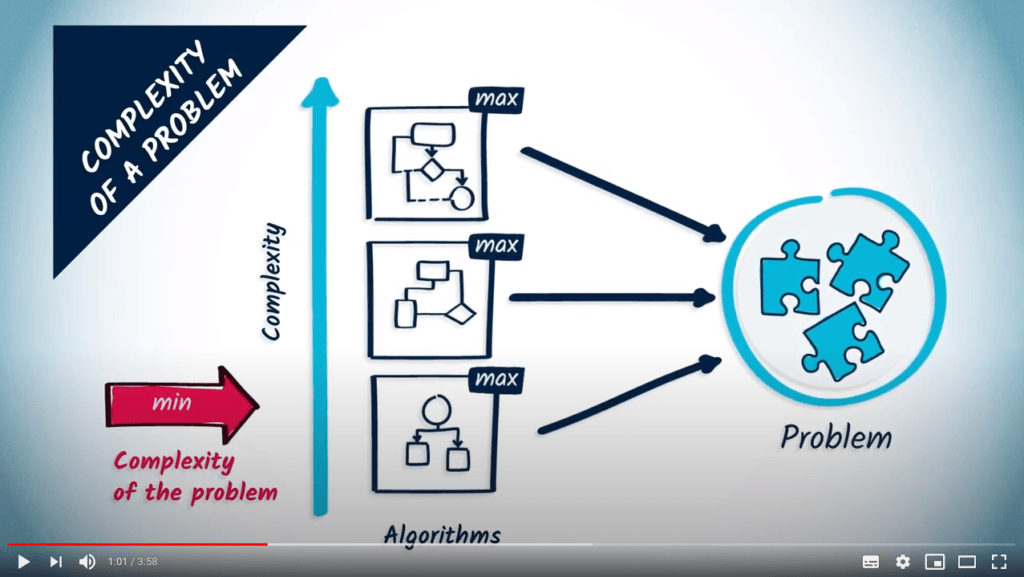
Jusqu’à présent, nous avons étudié la complexité des algorithmes, comme moyen d’estimer le temps nécessaire à leur exécution en fonction de leurs entrées. Plus généralement, les problèmes ont une notion de complexité. La complexité d’un problème est la meilleure complexité possible d’un algorithme qui le résout.

Points clés à retenir

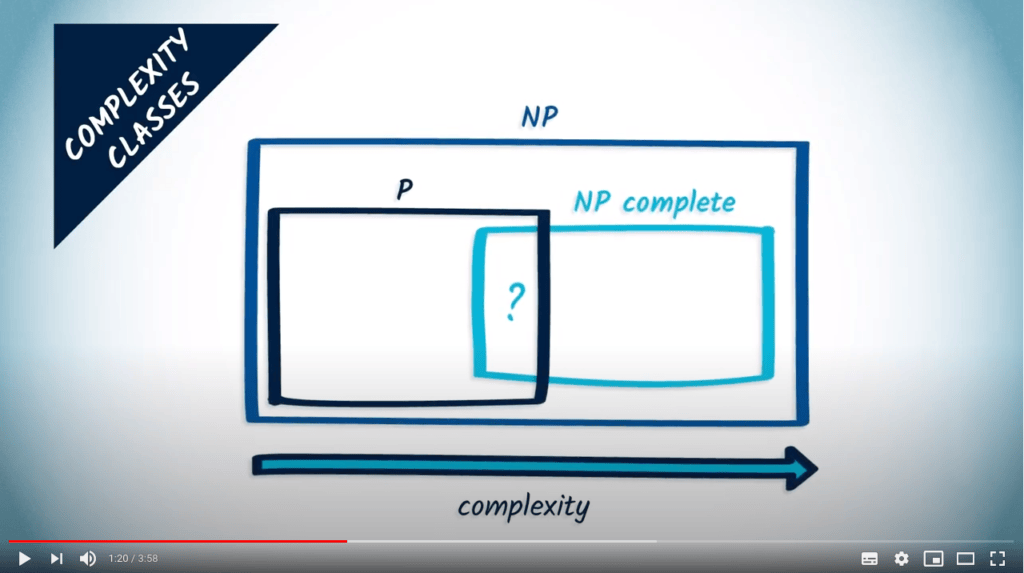
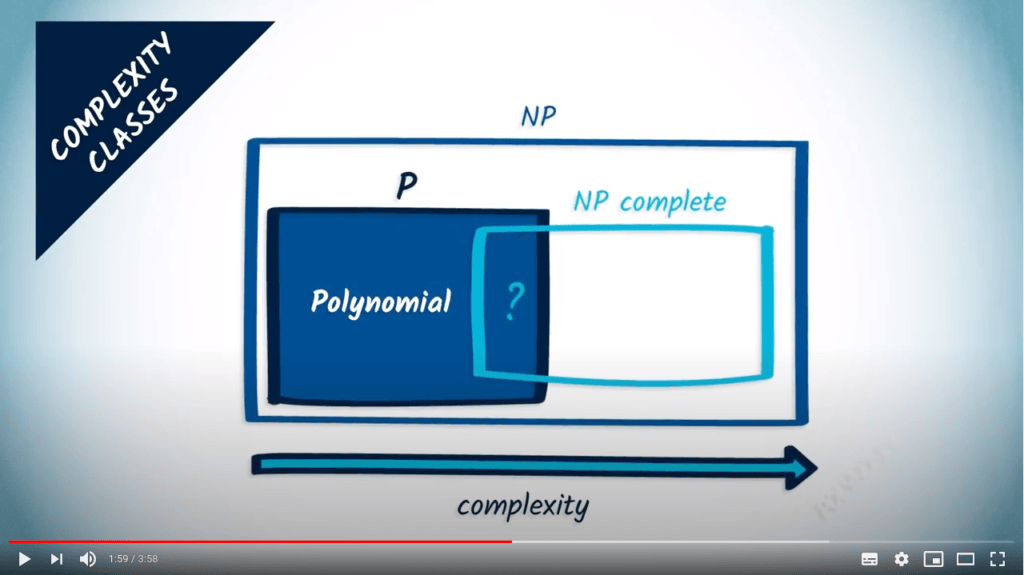
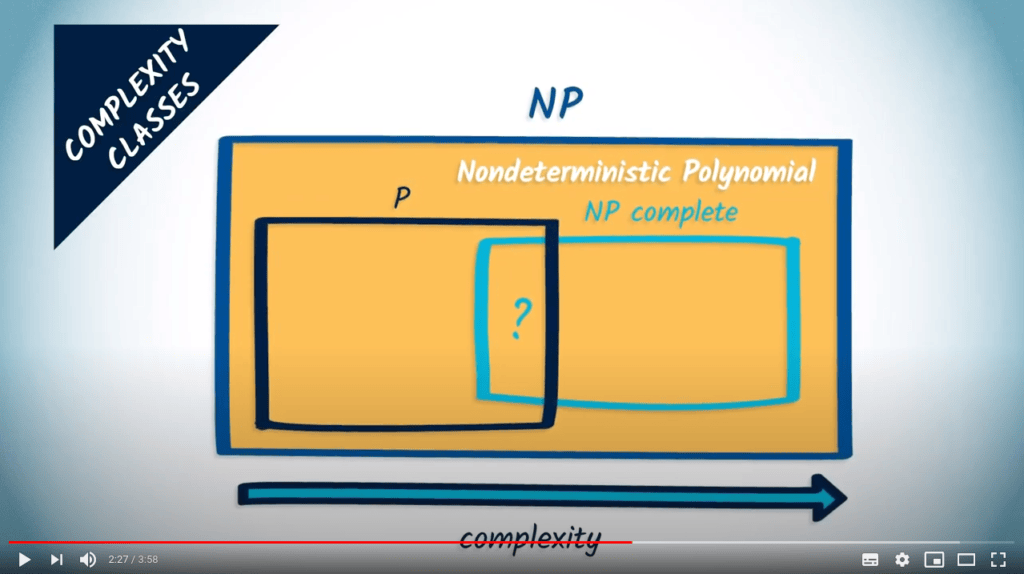
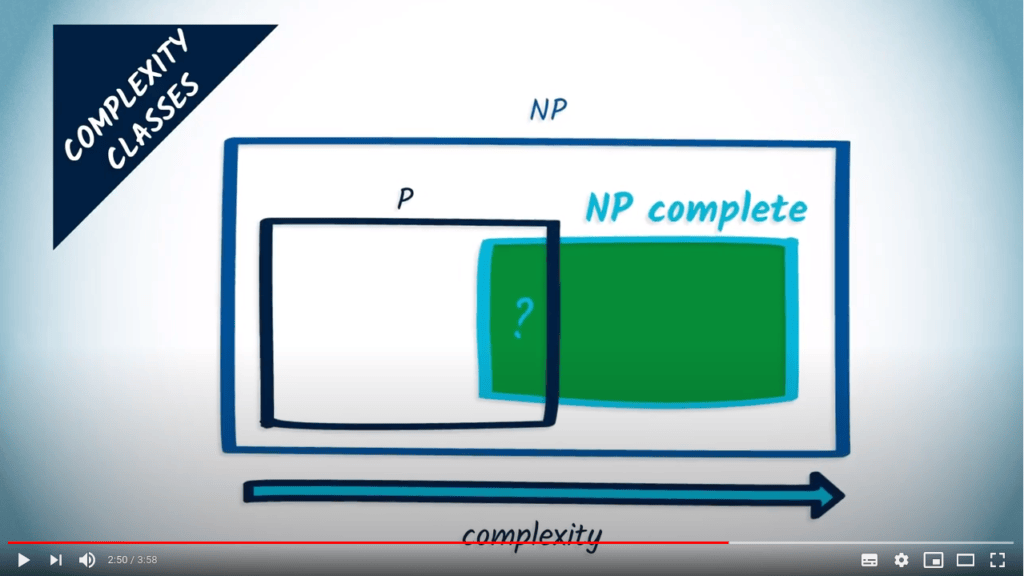
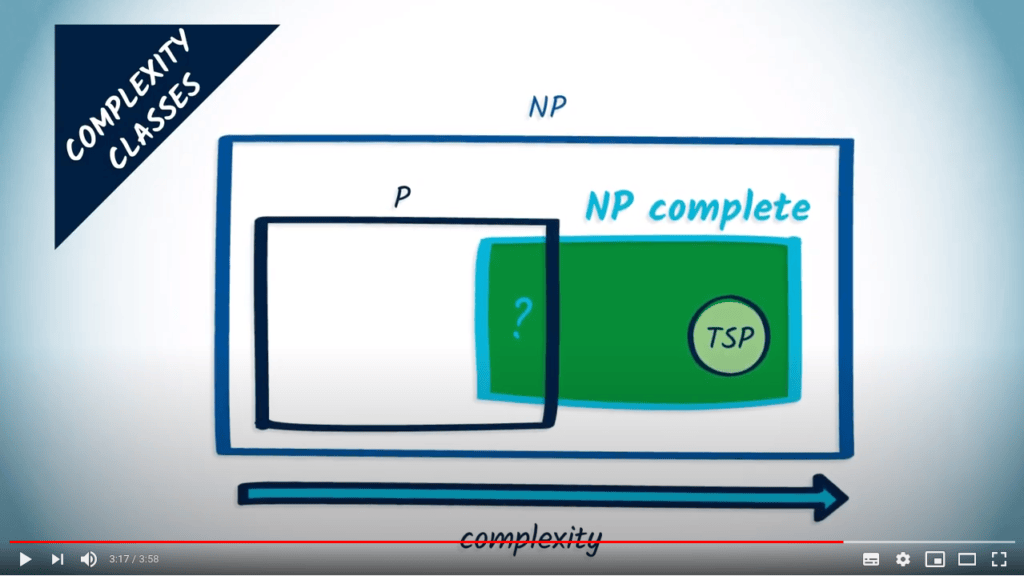
• Il existe des classes de complexité pour les problèmes.

• La complexité d’un problème décrit la complexité minimale d’un algorithme qui le résout.

• Il existe des intersections, des relations d’inclusion ou des équivalences entre certaines classes de complexité.

• La complexité peut également décrire la mémoire nécessaire pour résoudre un problème.

Contenu de l’article

Vidéo

Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Pour aller plus loin

Problèmes de décision et problèmes d’optimisation

Les classes P et NP sont définies pour des problèmes de décision, c’est-à-dire des problèmes dont la réponse est « oui » ou « non ». Or, le TSP tel que présenté dans la vidéo est un problème d’optimisation : on cherche le chemin le plus court, pas une réponse oui/non.

On associe donc au TSP sa version de décision : étant donné un graphe pondéré, un sommet de départ et une longueur $L$, existe-t-il un chemin partant de ce sommet, passant par tous les autres, et de longueur au plus $L$ ?

Les deux versions sont aussi difficiles l’une que l’autre, à un facteur polynomial près :

• Si l’on sait résoudre la version d’optimisation, on résout la version de décision : il suffit de comparer la longueur du meilleur chemin à $L$.

• Si l’on sait résoudre la version de décision, on trouve la longueur du meilleur chemin par dichotomie sur $L$, entre 0 et la somme de tous les poids $W$. Cela demande $O(log(W))$ appels, un nombre polynomial en la taille de l’entrée (les poids sont écrits avec $O(log(W))$ chiffres).

Vérifier une solution : la notion de certificat

Un problème de décision est dans NP si, lorsque la réponse est « oui », il existe une preuve de cette réponse, appelée certificat, que l’on peut vérifier en temps polynomial.

Pour la version de décision du TSP, le certificat est tout simplement un chemin. Le vérifier est facile : il suffit de contrôler qu’il passe une et une seule fois par chaque sommet, et que sa longueur ne dépasse pas $L$. Voici une fonction qui le fait, en temps linéaire en le nombre de sommets :

def check_solution ( distances:  dict[int, dict[int, int]],
                     source:     int,
                     path:       list[int],
                     max_length: int
                   ) ->          bool:

    """
    Checks whether a path is a solution to the decision version of the TSP.
    The path must start at the source, visit each vertex exactly once, and have a length of at most max_length.

    Args:
        distances:  The distances between all pairs of vertices (e.g., a meta-graph).
        source:     The vertex at which the path must start.
        path:       The candidate solution, as a list of vertices.
        max_length: The maximum length allowed for the path.

    Returns:
        True if the path is a solution, False otherwise.
    """

    # The path must start at the source, and contain each vertex exactly once
    if len(path) != len(distances) or set(path) != set(distances) or path[0] != source:
        return False

    # Its length must not exceed the bound
    length = sum(distances[path[i]][path[i + 1]] for i in range(len(path) - 1))
    return length <= max_length

C’est toute l’asymétrie des problèmes NP : vérifier une solution est rapide, alors que personne ne sait en trouver une rapidement. La question P = NP revient à se demander si cette asymétrie est réelle, ou si l’on n’a simplement pas encore trouvé les bons algorithmes.

Montrer qu’un problème est NP-complet

Pour montrer qu’un problème $Q$ est NP-complet, on procède en deux temps :

1. On montre que $Q$ est dans NP, en exhibant un certificat vérifiable en temps polynomial.
2. On montre que $Q$ est au moins aussi difficile qu’un problème déjà connu pour être NP-complet, en réduisant ce problème à $Q$ (voir l’article sur le TSP pour la notion de réduction).

Il faut bien un premier problème NP-complet pour démarrer : c’est le théorème de Cook-Levin (1971), qui montre que le problème de la satisfiabilité d’une formule logique (SAT) est NP-complet. À partir de lui, des milliers de problèmes ont été montrés NP-complets par réductions successives, à commencer par les 21 problèmes de Karp (1972).

Faisons-le pour la version de décision du TSP, dans sa variante où l’on revient au point de départ (on cherche alors un cycle et non un chemin). Le point 1 se fait comme plus haut, en ajoutant le retour au sommet de départ dans le calcul de la longueur. Pour le point 2, on part du problème du cycle hamiltonien, l’un des 21 problèmes de Karp : étant donné un graphe, existe-t-il un cycle qui passe une et une seule fois par chaque sommet ?

À partir d’un graphe $G$ à $n$ sommets, on construit un graphe complet sur les mêmes sommets, où une arête a un poids de 1 si elle existe dans $G$, et de 2 sinon. Alors, $G$ a un cycle hamiltonien si et seulement si ce graphe complet a un tour de longueur au plus $n$.

NP-complet ou NP-difficile ?

Attention, NP n’est pas la classe des problèmes difficiles : tout problème de P est aussi dans NP (P $\subseteq$ NP), car si l’on sait trouver la réponse en temps polynomial, on sait a fortiori la vérifier. Ce sont les problèmes NP-complets qui sont les plus difficiles de NP.

Un problème est dit NP-difficile s’il est au moins aussi difficile que tous les problèmes de NP, sans forcément être lui-même dans NP. Les problèmes NP-complets sont donc exactement les problèmes NP-difficiles qui sont dans NP.

La version d’optimisation du TSP est NP-difficile, mais elle n’est pas NP-complète au sens strict : ce n’est pas un problème de décision, donc elle ne peut pas être dans NP. C’est sa version de décision qui est NP-complète.

On pourrait espérer que les labyrinthes de PyRat, avec leur structure très particulière, rendent le problème plus facile. Ce n’est malheureusement pas évident : le problème du cycle hamiltonien reste NP-complet même dans les graphes en grille, c’est-à-dire des cases placées sur une grille et reliées à leurs voisines, comme un labyrinthe PyRat avec des trous mais sans murs (Itai, Papadimitriou et Szwarcfiter, 1982).

Complexité en espace

Les classes de complexité ci-dessus décrivent les besoins en temps pour résoudre les problèmes. Afin de mesurer d’autres besoins, tels que la consommation de mémoire, il existe d’autres classes de complexité.

De manière similaire à la complexité en temps, la complexité en espace mesure la plus petite quantité de mémoire dont un programme aurait besoin pour résoudre le problème en question, pour le pire cas d’entrée. Encore une fois, cela peut être vu comme un « minimum de maximum ».

Nous utilisons également les notations grand-O pour décrire l’utilisation de la mémoire, en fonction de la taille de l’entrée. Par exemple, $O(n)$ désigne une utilisation linéaire de la mémoire, et $O(n!)$ indique que le problème peut être résolu avec une quantité de mémoire qui croît au plus de manière factorielle avec la dimension de l’entrée.

Comme pour les classes de complexité en temps, il existe une énorme taxonomie des classes de complexité en espace.

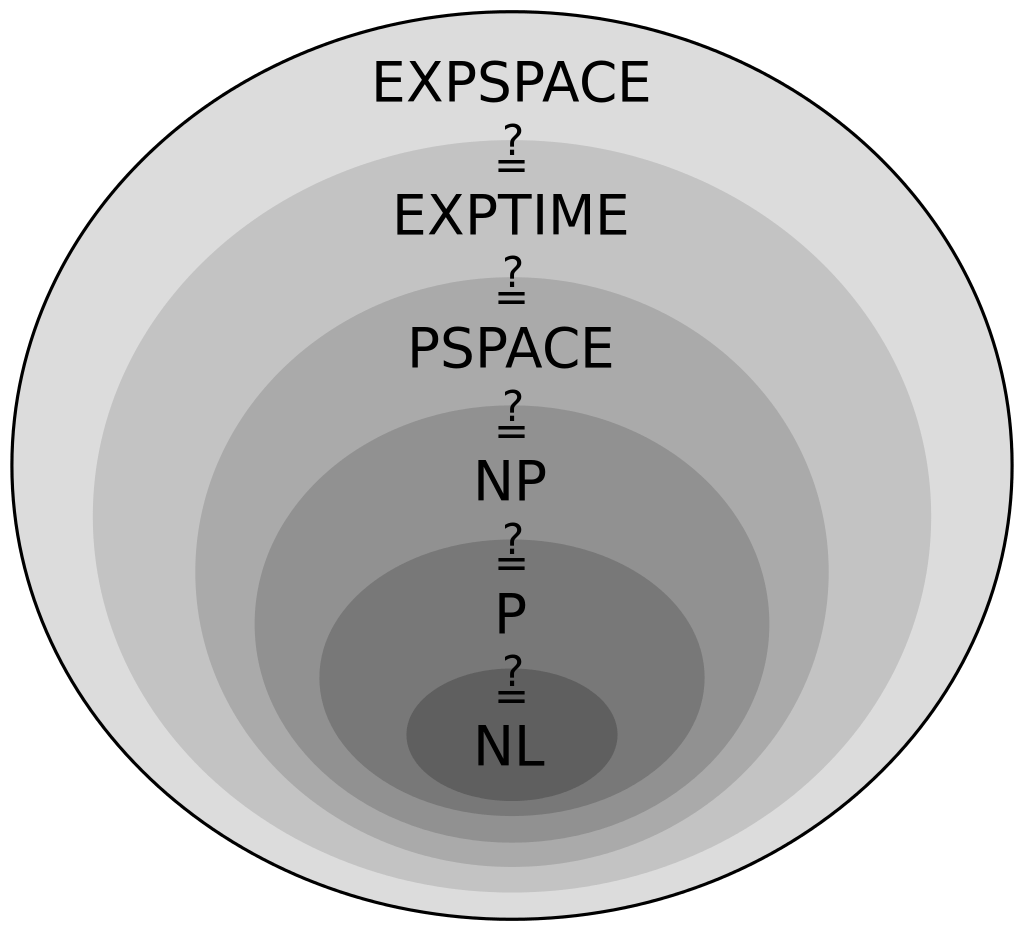
Parmi les classes classiques, PSPACE regroupe les problèmes de décision qui peuvent être résolus avec une quantité de mémoire polynomiale en la taille de l’entrée.

Les complexités en espace et en temps ne sont pas indépendantes. Par exemple, il a été montré que NP $\subseteq$ PSPACE. Cependant, il existe de nombreuses égalités entre classes qui sont inconnues, dont beaucoup sont des problèmes ouverts en recherche depuis des décennies.

Pour aller encore plus loin

• A taxonomy of complexity classes of functions

  Plein d’informations sur les différentes classes de complexité.
• Les 21 problèmes NP-complets de Karp

  La liste de problèmes qui a lancé l’étude de la NP-complétude, et les réductions qui les relient.
• P = NP ?

  Le problème de déterminer si P et NP sont identiques est un problème majeur en informatique.