Solutions approchées
Temps de lecture25 minEn bref
Résumé de l’article
Comme mentionné dans les autres articles, les heuristiques fournissent des solutions approchées. Ici, nous donnons plus de détails sur la façon de caractériser la qualité d’une telle solution. En particulier, nous nous concentrerons sur la correction et le gain temporel.
À retenir
-
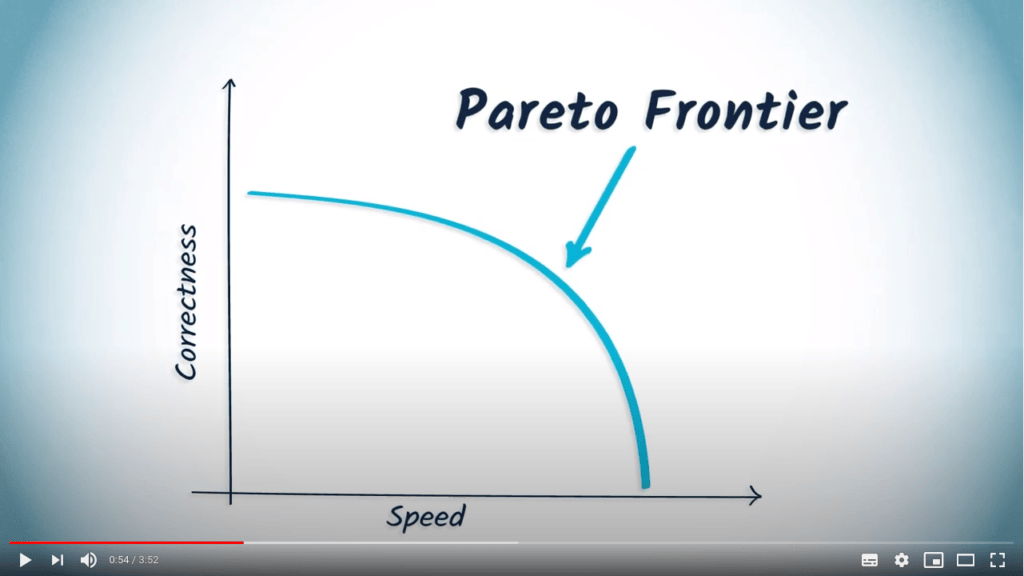
Une solution approchée est un compromis entre qualité de la solution et temps requis pour l’obtenir.
-
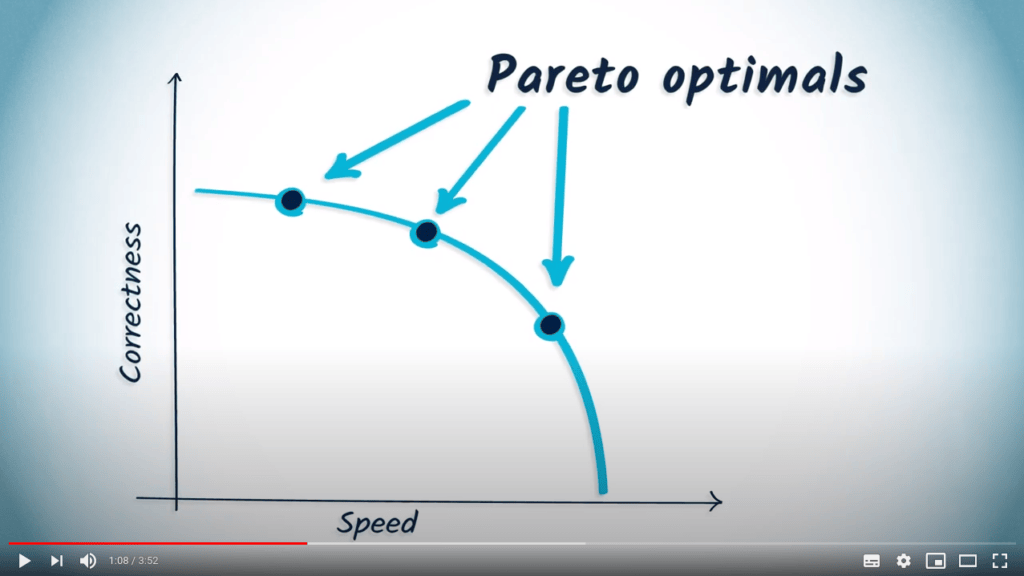
Les solutions qui sont des compromis optimaux de plusieurs critères sont appelées Pareto-optimales.
Contenu de l’article
1 — Vidéo
Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.
Pour aller plus loin
2 — Exemple de la coloration de graphes
2.1 — L’algorithme exact
Prenons l’exemple suivant : nous appelons “coloration d’un graphe” un vecteur d’entiers, chacun associé à l’un de ses sommets. Ces entiers sont appelés couleurs de sommet, et peuvent être identiques.
Une coloration est dite “propre” si tous les sommets reliés par une arête sont de couleurs différentes. Le “nombre chromatique d’un graphe” est le nombre minimum de couleurs qui apparaissent dans une coloration spécifique.
Ce problème est un exemple connu de problème NP-Complet. Une façon de le résoudre avec précision est de lister toutes les colorations possibles à 1 couleur, puis à 2 couleurs, etc. jusqu’à trouver une coloration propre.
Le code Python suivant résout le problème comme décrit ci-dessus :
# For easy iteration over permutations
import itertools
# Function to check if a coloring is correct
# A coloring is correct if no neighbors share a color
def check_coloring (graph, colors):
for vertex in range(len(graph)):
for neighbor in graph[vertex]:
if colors[vertex] == colors[neighbor]:
return False
return True
# This function returns a coloring of the given graph using a minimum number of colors
# We progressively increase the number of available colors
# For each number, we test all possible color arrangements
def exhaustive_coloring (graph):
for nb_colors in range(len(graph)):
for coloring in itertools.product(range(nb_colors), repeat=len(graph)):
print("Nb colors:", nb_colors, "- Candidate coloring:", coloring)
if check_coloring(graph, coloring):
return coloring
# Test graph
# Here, we represent graphs as an adjacency list
graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]
result = exhaustive_coloring(graph)
print(result)Dans cet exemple, un graphe est implémenté sous la forme d’une liste de listes. Il contient 6 sommets (nommés $v_1$ à $v_6$), et 8 arêtes (symétriques). La solution retournée par l’algorithme est :
[0, 1, 2, 0, 1, 2]Cela indique que trois couleurs suffisent pour avoir une coloration propre du graphe, avec :
- $v_1$ et $v_4$ partageant la couleur 0.
- $v_2$ et $v_5$ partageant la couleur 1.
- $v_3$ et $v_6$ partageant la couleur 2.
2.2 — L’approche gloutonne
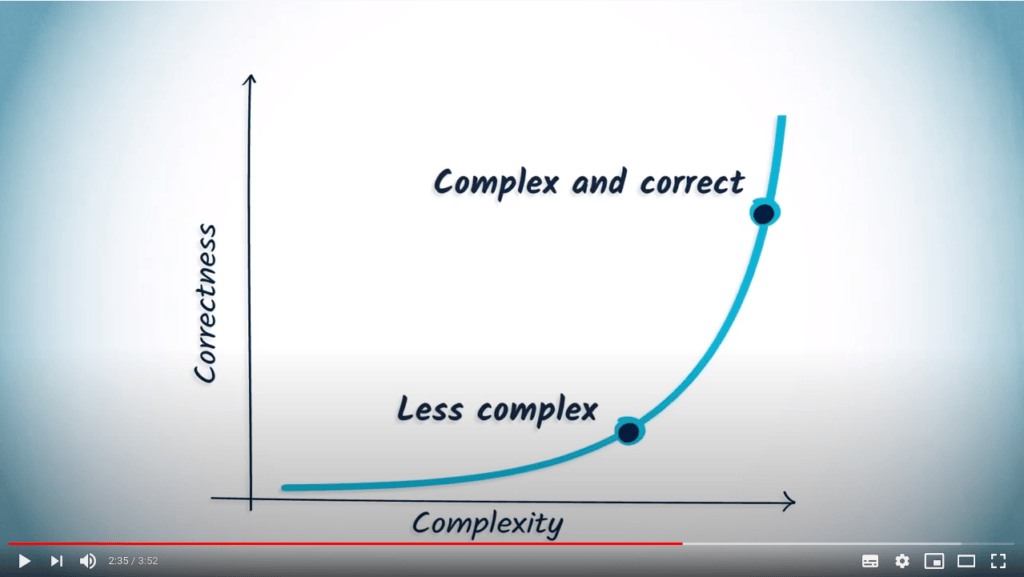
Cet algorithme est très complexe et une solution approchées bien connue consiste à trier les sommets par nombre décroissant de voisins, en les coloriant dans cet ordre en choisissant la plus petite couleur positive qui laisse la coloration propre. Cet algorithme approché est décrit ci-dessous :
# For min heaps
import heapq
# Function to check if a coloring is correct
# A coloring is correct if no neighbors share a color
def check_coloring (graph, colors):
for vertex in range(len(graph)):
if colors[vertex] is not None:
for neighbor in graph[vertex]:
if colors[neighbor] is not None:
if colors[vertex] == colors[neighbor]:
return False
return True
# This function tries to greedily color the graph from the highest degree node to the lowest
# First, we sort the nodes in descending order of degree using a max heap (negative min heap)
# Then we color the nodes using this heap
def greedy_coloring (graph):
heap = []
for vertex in range(len(graph)):
heapq.heappush(heap, (-len(graph[vertex]), vertex))
colors = [None] * len(graph)
while len(heap) > 0:
degree, vertex = heapq.heappop(heap)
for color in range(len(graph)):
colors[vertex] = color
if check_coloring(graph, colors):
break
return colors
# Test graph
graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]
result = greedy_coloring(graph)
print(result)Cet algorithme est beaucoup moins complexe que le précédent, et permet donc de considérer des graphes avec beaucoup plus de sommets. Ici, nous obtenons le résultat suivant :
[0, 1, 2, 0, 1, 2]Notez qu’ici, nous trouvons le même résultat que l’algorithme exhaustif. Cependant, ce n’est pas toujours le cas.
2.3 — Simulations
Afin d’évaluer la qualité de notre algorithme approché, nous nous concentrerons sur deux choses : le temps de calcul et la précision. Pour tester ces deux quantités, nous allons faire la moyenne des résultats sur un grand nombre de graphes aléatoires.
Afin d’automatiser un peu les choses, nous allons adapter nos codes pour prendre des arguments en ligne de commande et produire un fichier exploitable. Créons deux fichiers Python.
Le programme suivant, measure_greedy.py, retourne le temps d’exécution moyen de l’approche gloutonne pour résoudre le problème considéré, ainsi que le nombre moyen de couleurs nécessaires pour un graphe de taille fixe :
# Various imports
import math
import random
import heapq
import time
import sys
# Arguments
NB_NODES = int(sys.argv[1])
EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES
NB_TESTS = int(sys.argv[2])
# Set a fixed random seed to compare scripts on the same graphs
random.seed(NB_NODES)
# Generates a random Erdős-Rényi graph
def generate_graph():
graph = [[] for i in range(NB_NODES)]
for i in range(NB_NODES):
for j in range(i + 1, NB_NODES):
if random.random() < EDGE_PROBABILITY:
graph[i].append(j)
graph[j].append(i)
return graph
# Function to check if a coloring is correct
# A coloring is correct if no neighbors share a color
def check_coloring(graph, colors):
for vertex in range(len(graph)):
if colors[vertex] is not None:
for neighbor in graph[vertex]:
if colors[neighbor] is not None:
if colors[vertex] == colors[neighbor]:
return False
return True
# This function tries to greedily color the graph from the highest degree node to the lowest
# First, we sort the nodes in descending order of degree using a max heap (negative min heap)
# Then we color the nodes using this heap
def greedy_coloring(graph):
heap = []
for vertex in range(len(graph)):
heapq.heappush(heap, (-len(graph[vertex]), vertex))
colors = [None] * len(graph)
while len(heap) > 0:
degree, vertex = heapq.heappop(heap)
for color in range(len(graph)):
colors[vertex] = color
if check_coloring(graph, colors):
break
return colors
# Tests
average_time = 0.0
average_solution_length = 0.0
for i in range(NB_TESTS):
graph = generate_graph()
time_start = time.time()
solution = greedy_coloring(graph)
average_solution_length += len(set(solution)) / NB_TESTS
average_time += (time.time() - time_start) / NB_TESTS
# Display average time based on problem size
print(NB_NODES, ";", average_time, ";", average_solution_length)De même, le programme suivant measure_exhaustive.py évalue la solution exhaustive :
# Various imports
import math
import random
import time
import sys
import itertools
# Arguments
NB_NODES = int(sys.argv[1])
EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES
NB_TESTS = int(sys.argv[2])
# Set a fixed random seed to compare scripts on the same graphs
random.seed(NB_NODES)
# Generates a random Erdős-Rényi graph
def generate_graph():
graph = [[] for i in range(NB_NODES)]
for i in range(NB_NODES):
for j in range(i + 1, NB_NODES):
if random.random() < EDGE_PROBABILITY:
graph[i].append(j)
graph[j].append(i)
return graph
# Function to check if a coloring is correct
# A coloring is correct if no neighbors share a color
def check_coloring(graph, colors):
for vertex in range(len(graph)):
for neighbor in graph[vertex]:
if colors[vertex] == colors[neighbor]:
return False
return True
# This function returns a coloring of the given graph using a minimum number of colors
# We progressively increase the number of available colors
# For each number, we test all possible color arrangements
def exhaustive_coloring(graph):
for nb_colors in range(len(graph)):
for coloring in itertools.product(range(nb_colors), repeat=len(graph)):
print("Nb colors:", nb_colors, "- Candidate coloring:", coloring)
if check_coloring(graph, coloring):
return coloring
# Tests
average_time = 0.0
average_solution_length = 0.0
for i in range(NB_TESTS):
graph = generate_graph()
time_start = time.time()
solution = exhaustive_coloring(graph)
average_solution_length += len(set(solution)) / NB_TESTS
average_time += (time.time() - time_start) / NB_TESTS
# Display average time based on problem size
print(NB_NODES, ";", average_time, ";", average_solution_length)Nous pouvons maintenant exécuter les commandes suivantes pour lancer les deux algorithmes sur des graphes aléatoires (100 graphes par ordre de graphe). La recherche exhaustive ne sera évaluée que sur un sous-ensemble des ordres de graphe en raison de considérations de temps :
@echo off
for /l %%n in (5,1,100) do (
python measure_greedy.py %%n 100 >> results_greedy.csv
)for ($n = 5; $n -le 100; $n++) {
python measure_greedy.py $n 100 >> results_greedy.csv
}for n in {5..100}; do
python3 measure_greedy.py $n 100 >> results_greedy.csv
donefor n in {5..100}; do
python3 measure_greedy.py $n 100 >> results_greedy.csv
done@echo off
for /l %%n in (5,1,20) do (
python measure_exhaustive.py %%n 100 >> results_exhaustive.csv
)for ($n = 5; $n -le 20; $n++) {
python measure_exhaustive.py $n 100 >> results_exhaustive.csv
}for n in {5..20}; do
python3 measure_exhaustive.py $n 100 >> results_exhaustive.csv
donefor n in {5..20}; do
python3 measure_exhaustive.py $n 100 >> results_exhaustive.csv
doneComparons les temps d’exécution en utilisant Libreoffice :
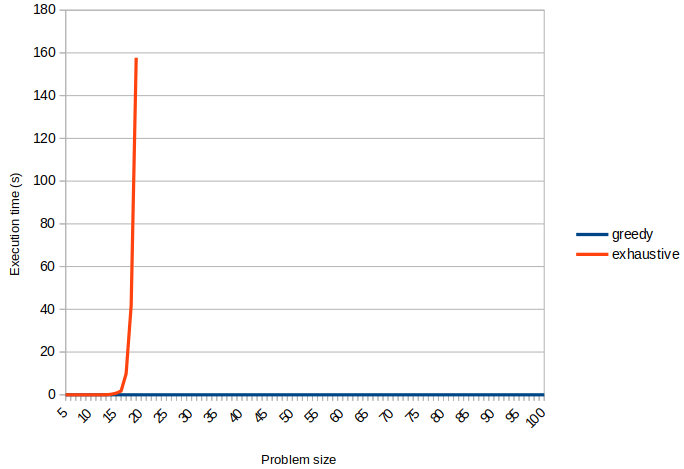
Clairement, le gain en temps d’exécution est significatif. De même, comparons les nombres chromatiques moyens trouvés pour les deux algorithmes :
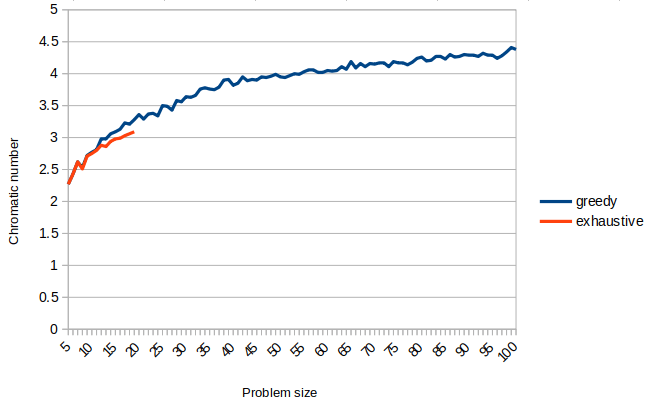
En regardant la courbe de précision, il semble que la perte de précision n’est pas très élevée, du moins pour les tailles de problème qui ont pu être calculées en utilisant l’approche exhaustive. Pour des graphes plus grands, nous ne pouvons pas calculer la solution exacte en raison de la complexité pour la trouver.
Afin d’évaluer un peu plus cet aspect, nous allons évaluer les solutions trouvées en utilisant l’approche gloutonne sur des graphes bipartis, pour lesquels nous savons que le nombre chromatique est toujours 2 :
# Generates a random bipartite Erdős-Rényi graph
def generate_bipartite_graph ():
graph = [[] for i in range(NB_NODES)]
for i in range(NB_NODES):
for j in range(i + 1, NB_NODES):
if i % 2 != j % 2 and random.random() < EDGE_PROBABILITY:
graph[i].append(j)
graph[j].append(i)
return graphNous obtenons les résultats suivants :
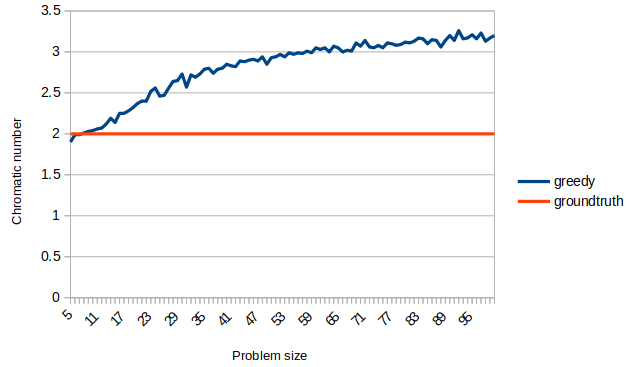
Ici encore, le résultat semble raisonnable, ce qui nous amène à penser que cette heuristique est bien adaptée au problème.
Vous devriez tout de même noter que pour de petites tailles de problème, le nombre chromatique trouvé est parfois inférieur à 2, ce qui semble erroné. Cependant, notez que le générateur de graphes aléatoires ne vérifie pas la connexité du graphe, ce qui peut conduire à des graphes à plusieurs composantes connexes.
Pour aller encore plus loin
-
Ici, nous avons étudié les compromis temps/précision, mais c’est un concept plus général.
-
Si vous voulez en savoir plus sur ces graphes particuliers.