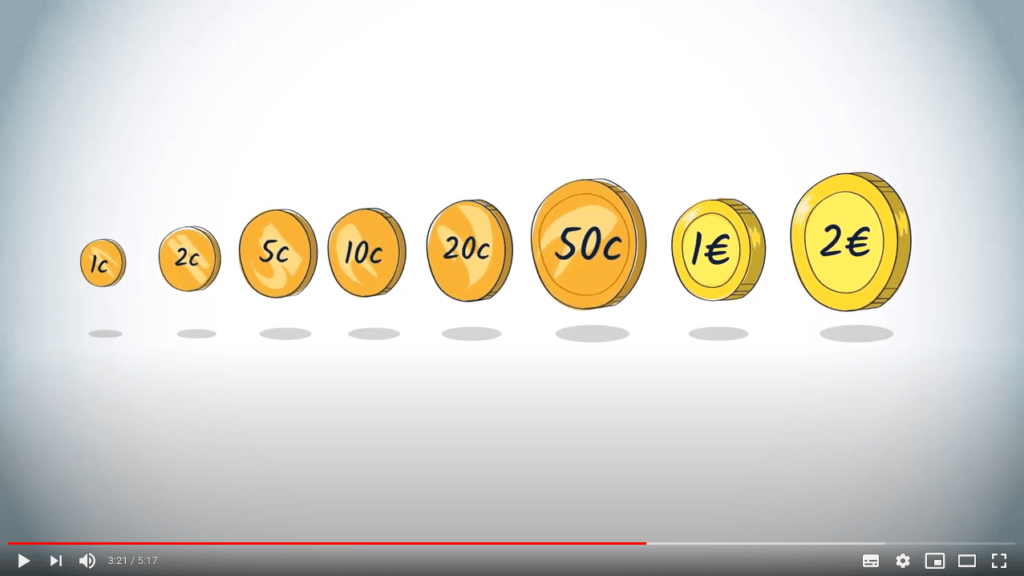Algorithmes gloutons

Temps de lecture10 min

En bref

Résumé de l’article

Dans cet article, vous allez découvrir les algorithmes gloutons. Ces algorithmes sont des algorithmes heuristiques qui visent à approximer la solution d’un problème complexe. Pour ce faire, ils considèrent un problème d’optimisation global, et approximent sa solution en résolvant une série de sous-problèmes localement optimaux.

Points clés à retenir

  • Les algorithmes gloutons approximent une solution globale avec une série de solutions locales.

  • Le choix d’une telle optimisation locale est une heuristique.

  • Par exemple, un algorithme glouton pour approximer le TSP peut utiliser l’heuristique “toujours aller vers le voisin non visité le plus proche”.

  • Sur certains problèmes spécifiques, un algorithme glouton peut être optimal.

Contenu de l’article

Vidéo

Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Information
Cliquez ici pour afficher la traduction de la vidéo.

Bonjour ! C’est encore moi. Je vois que vous avez faim d’en savoir plus sur la théorie des graphes. Moi aussi !

Parfois, lorsqu’un problème est trop complexe à résoudre, on utilise des algorithmes d’approximation. Les algorithmes d’approximation fournissent une solution proche de la solution exacte, mais dans un temps beaucoup plus court. Un exemple d’algorithmes d’approximation sont les algorithmes gloutons.

Principe

Le but d’un algorithme glouton est d’approximer la solution d’un problème par une succession de solutions localement optimales. Pour illustrer cela, considérons le problème du voyageur de commerce, le TSP, dont nous avons vu qu’il est un problème complexe à résoudre.

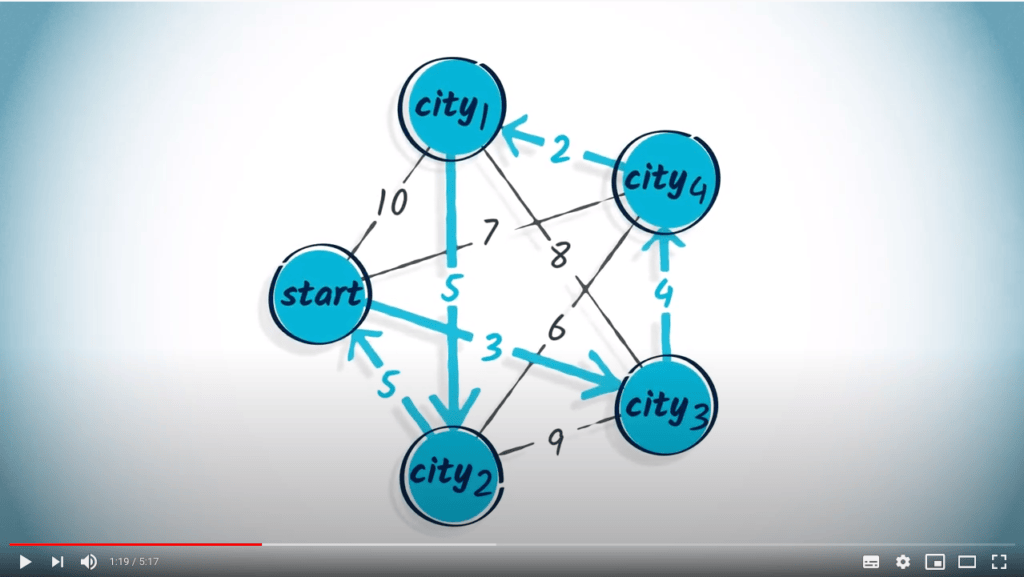
Au lieu de chercher une solution exacte, nous pouvons choisir d’aller toujours vers le sommet non exploré le plus proche du sommet où nous nous trouvons actuellement. Il s’agit d’un algorithme glouton car, à chaque étape, la distance à parcourir est minimisée, un pas à la fois. Nous avons donc pris des décisions localement optimales.

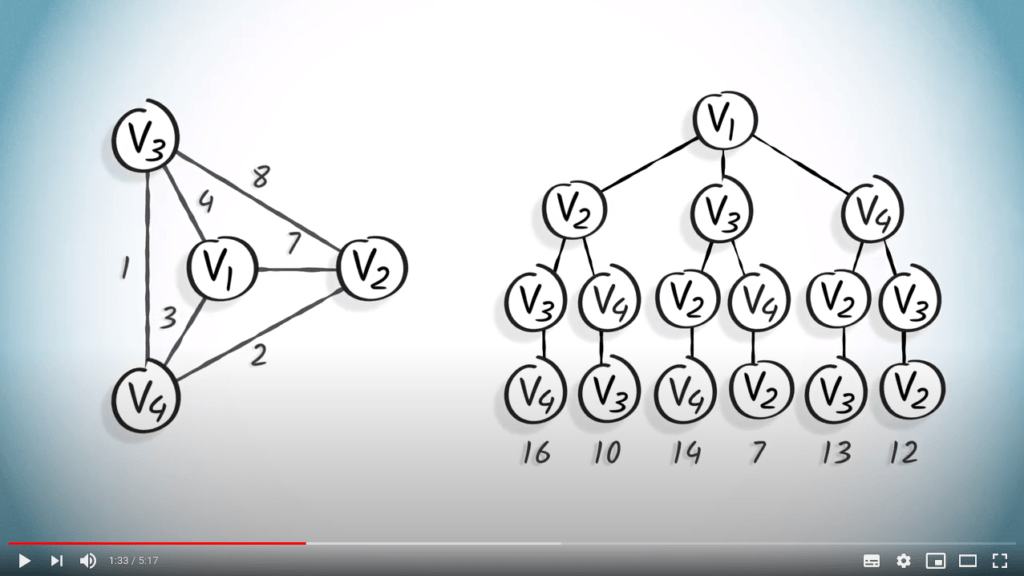
Cependant, cette solution n’est pas nécessairement optimale. Prenons le graphe suivant comme exemple, pour lequel nous explorons tous les chemins possibles.

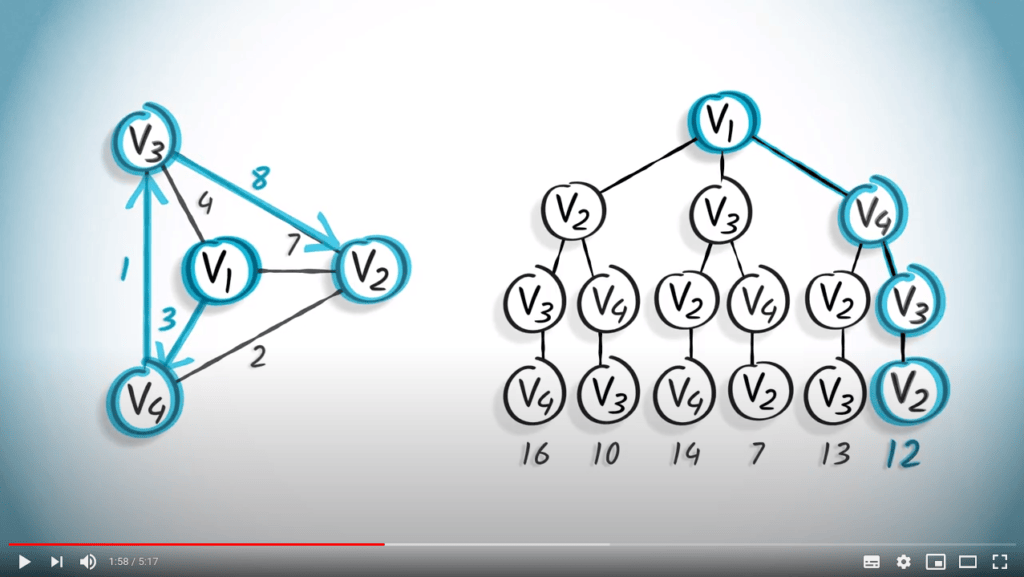
Mettons l’algorithme glouton en pratique. En partant du sommet $v_1$, nous irons d’abord vers $v_4$, car l’arête correspondante est la plus courte de toutes les possibilités. En utilisant le même principe, nous nous déplacerons ensuite vers $v_3$ et enfin vers $v_2$. N’est-ce pas ? Dans cet exemple, le chemin obtenu a une longueur totale de 12.

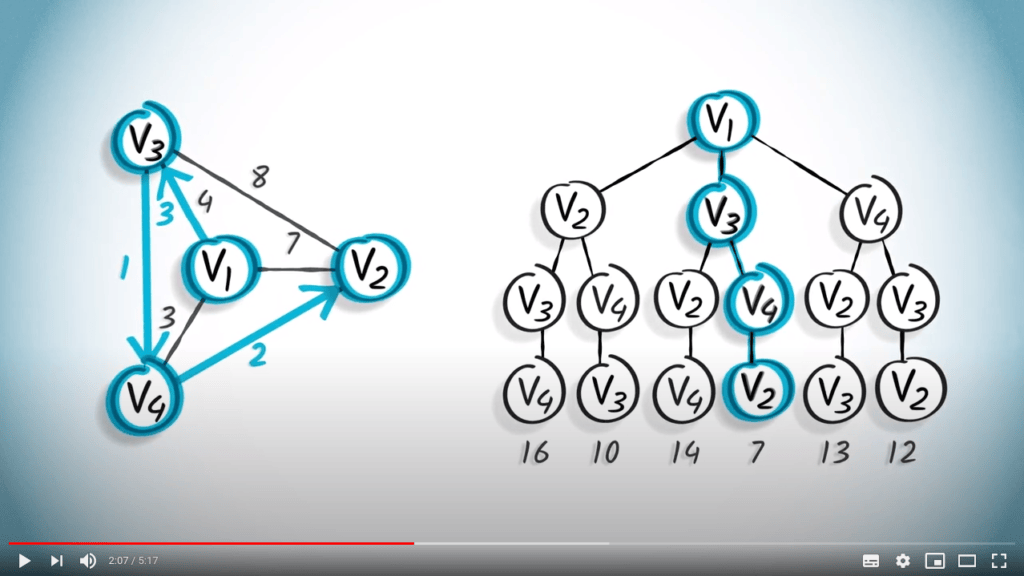
Cependant, la solution optimale est un chemin qui a une longueur de 7, qui est le chemin $( \{v_1,v_3\}, \{v_3,v_4\}, \{v_2,v_4\} )$.

N’oubliez pas, cet algorithme n’est qu’un exemple d’algorithme glouton pour résoudre le TSP. En plus de choisir systématiquement le voisin le plus proche, qui était l’exemple que nous venons de voir, d’autres heuristiques peuvent être utilisées.

Voici quelques exemples :

Vous pouvez choisir le chemin de longueur minimale en explorant $k$ sommets restants ($k = 2, 3, \dots$) : si $k = 1$, il s’agit de l’algorithme glouton simple que nous venons de voir. Vous pouvez choisir d’aller vers une zone dense d’un labyrinthe où il y a beaucoup de morceaux de fromage à trouver. Ou bien, vous pouvez choisir de lancer aléatoirement plusieurs recherches possibles, et retenir la meilleure option.

Un cas où l'algorithme glouton est optimal

Dans certains cas, les algorithmes gloutons peuvent être optimaux.

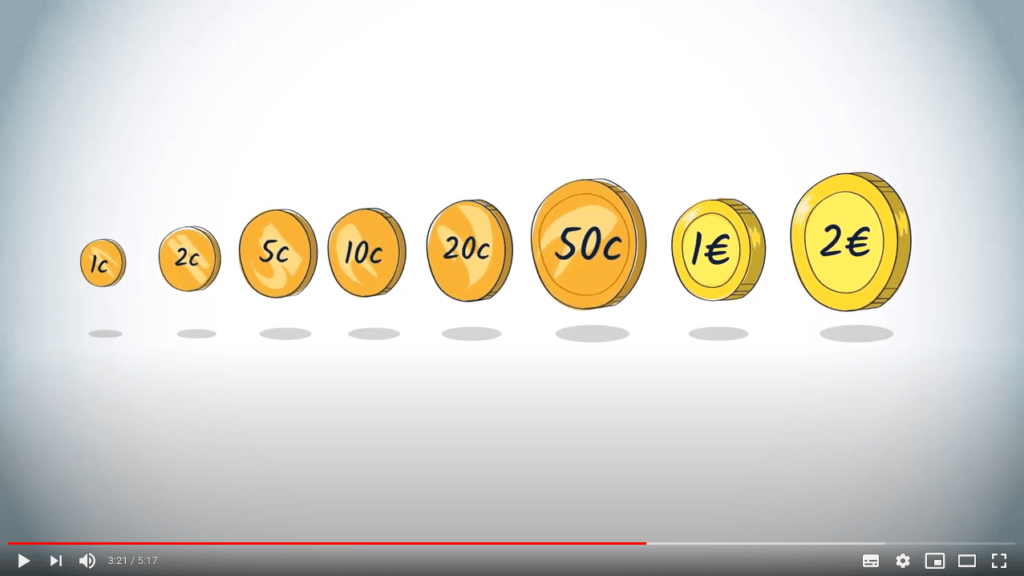
Considérons le problème du rendu de monnaie après un paiement. Nous souhaitons rendre une certaine somme de monnaie en euros, et nous avons les pièces suivantes : 1c, 2c, 5c, 10c, 20c, 50c, 1€, 2€. L’objectif est d’utiliser le moins de pièces possible.

Un algorithme glouton typique consiste à sélectionner la pièce de valeur la plus élevée possible, inférieure ou égale à la somme qui doit être rendue, jusqu’au point où la monnaie restante à rendre est 0. Donc, si vous voulez rendre 3,27€, alors l’algorithme rendra d’abord 2€ (laissant 1,27€ à rendre), puis 1€ (laissant 27c à rendre), 20c (laissant 7c à rendre), 5c (laissant 2c à rendre), et enfin 2c.

En cherchant toutes les combinaisons possibles, on peut voir que c’est bien la solution optimale. Pour montrer cela, il suffit de remarquer que chaque pièce a une valeur au moins égale au double de la pièce de valeur inférieure. Cela signifie qu’il sera toujours plus efficace de donner la priorité à la pièce de valeur supérieure, car une pièce sera rendue au lieu de plusieurs.

Considérons maintenant les pièces suivantes : 1c, 2c, 5c, 10c, 20c, 40c, 50c, 1€, et dans ce cas nous voulons rendre 80c. L’algorithme glouton rendra 50c (reste 30c), puis 20c (reste 10c) et 10c, soit trois pièces.

Cependant, rendre 80c peut également se faire en rendant deux pièces de 40c. Dans ce cas, un algorithme glouton n’est pas optimal.

Conclusion

Pour récapituler, cette leçon vous a présenté les algorithmes gloutons pour trouver des solutions approximatives à des problèmes complexes tels que le TSP. À la prochaine !

Pour aller plus loin

Quand un algorithme glouton est-il optimal ?

Vous avez déjà rencontré des algorithmes gloutons optimaux, parfois sans le savoir :

  • L’algorithme de Dijkstra (séance 3) choisit à chaque étape le sommet non exploré le plus proche de la source, et ne revient jamais sur ce choix. Avec des poids positifs, ce choix local est toujours le bon.
  • Les algorithmes de Prim et de Kruskal construisent un arbre couvrant de poids minimal en ajoutant à chaque étape l’arête la plus légère possible : parmi celles qui ne créent pas de cycle pour Kruskal, et parmi celles qui étendent l’arbre en construction pour Prim.
  • La planification d’intervalles : pour choisir le plus grand nombre possible de réunions qui ne se chevauchent pas, il suffit de prendre à chaque fois celle qui se termine le plus tôt (voir la vidéo dans la section suivante).

Pour prouver qu’un algorithme glouton est optimal, on utilise souvent un argument d’échange : on part d’une solution optimale quelconque, et on montre qu’on peut la transformer, sans la rendre moins bonne, en une solution qui fait le même premier choix que l’algorithme glouton. En répétant l’argument choix après choix, on obtient que la solution gloutonne est elle aussi optimale.

Attention, l’argument donné dans la vidéo pour le rendu de monnaie (chaque pièce vaut au moins le double de la précédente) ne suffit pas en général. Avec des pièces de 1, 4 et 9 centimes, cette condition est vérifiée, et pourtant, pour rendre 12 centimes, l’algorithme glouton rend $9 + 1 + 1 + 1$ (quatre pièces), alors que $4 + 4 + 4$ n’en utilise que trois. Les systèmes de pièces pour lesquels l’algorithme glouton est toujours optimal sont appelés canoniques, et c’est heureusement le cas des euros. Pour vérifier qu’un système est canonique, il n’est pas nécessaire de tester toutes les sommes : s’il existe une somme pour laquelle l’algorithme glouton n’est pas optimal, il en existe une plus petite que la somme des deux plus grandes pièces (Kozen et Zaks, 1994).

Quelle garantie pour le plus proche voisin ?

Pour le TSP, l’algorithme glouton du plus proche voisin n’est pas optimal. Mais à quel point peut-il se tromper ?

  • Sans hypothèse sur le graphe, il peut être aussi mauvais qu’on le souhaite. Prenons quatre sommets $s$, $a$, $b$ et $c$, avec $d(s, a) = 1$, $d(a, b) = 1$, $d(s, c) = 2$, $d(a, c) = 2$, $d(s, b) = 3$, et $d(b, c) = M$ très grand. Depuis $s$, l’algorithme glouton va en $a$, puis en $b$, et doit finir par l’arête de poids $M$ : son chemin a une longueur $M + 2$. Le chemin $(s, c, a, b)$, lui, a une longueur de 5. En augmentant $M$, le rapport entre les deux devient aussi grand qu’on le veut.

  • Si le graphe vérifie l’inégalité triangulaire, ce qui est le cas des méta-graphes PyRat (voir l’article sur le TSP), un tel piège n’est plus possible. On sait alors que le chemin glouton est au pire de l’ordre de $\log(n)$ fois plus long que le chemin optimal, pour $n$ sommets (Rosenkrantz, Stearns et Lewis, 1977), et qu’on ne peut pas garantir mieux en général.

En pratique, l’algorithme glouton fait bien mieux que ce pire cas : dans l’activité pratique, vous mesurerez qu’il fait de l’ordre de 10 à 20% de tours en trop dans un labyrinthe PyRat.

Un algorithme glouton avec une garantie

Il existe un algorithme simple, construit à partir d’un algorithme glouton, qui garantit un chemin au plus deux fois plus long que l’optimal, lorsque le graphe vérifie l’inégalité triangulaire :

  1. Calculer un arbre couvrant de poids minimal du méta-graphe, par exemple avec l’algorithme glouton de Prim. La méthode minimum_spanning_tree() de la classe Graph de PyRat le fait pour vous, avec l’algorithme de Prim.
  2. Parcourir cet arbre en profondeur depuis la position de départ, et visiter les morceaux de fromage dans l’ordre où le parcours les découvre.

Pourquoi cela fonctionne-t-il ?

  • Le chemin optimal passe par tous les sommets sans cycle : c’est donc lui-même un arbre couvrant. Son poids est donc au moins celui de l’arbre couvrant de poids minimal.
  • Un parcours en profondeur de l’arbre emprunte chaque arête deux fois (une fois à l’aller, une fois au retour) : sa longueur est donc au plus deux fois le poids de l’arbre.
  • Visiter les sommets dans l’ordre de découverte revient à prendre des raccourcis dans ce parcours, ce qui, grâce à l’inégalité triangulaire, ne peut pas l’allonger.

Le chemin obtenu est donc au plus deux fois plus long que l’arbre, et donc au plus deux fois plus long que le chemin optimal. L’algorithme de Christofides, présenté dans l’article sur le TSP, améliore cette garantie à 1,5 fois l’optimal pour les tournées, au prix d’un calcul plus complexe.

Pour aller encore plus loin