Heuristiques

Temps de lecture15 min

En bref

Résumé de l’article

Dans cet article, vous découvrirez les heuristiques. Ce type d’algorithme permet d’approximer la solution d’un problème trop complexe pour être résolu de manière exacte.

À retenir

  • Une heuristique permet de trouver des solutions approximatives à un problème.

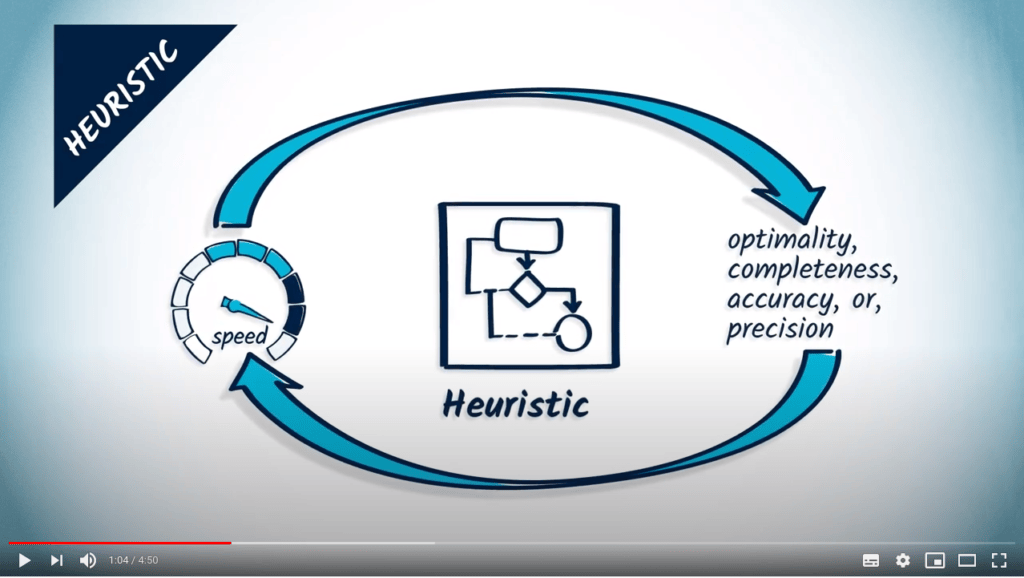
  • C’est un compromis entre la qualité de la solution trouvée et le temps de calcul nécessaire.

  • Elle encode une intuition sur la manière d’approximer une solution à un problème complexe.

  • Parfois, les heuristiques peuvent trouver des solutions optimales.

Contenu de l’article

1 — Vidéo

Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Information

Bonjour ! Ravi de voir que vous êtes arrivé à la semaine 5. Faisons un petit récapitulatif.

Dans la dernière leçon, nous avons vu que le problème du voyageur de commerce (ou TSP) est complexe à résoudre. Cependant, il est possible de réduire drastiquement la complexité de l’algorithme de résolution, à condition que la solution produite ne soit pas nécessairement optimale, mais suffisamment bonne.

Dans cette leçon, je vais introduire la notion d’algorithme heuristique, qui est une technique utilisée pour résoudre plus rapidement des problèmes lorsque les méthodes classiques sont trop lentes pour trouver une solution exacte. En d’autres termes, l’objectif d’une heuristique est de produire une solution dans un délai raisonnable qui soit suffisamment bonne pour résoudre le problème en question.

Généralement, les heuristiques sacrifient l’optimalité, la complétude, l’exactitude ou la précision au profit de la vitesse. D’une certaine manière, une heuristique peut être considérée comme un raccourci.

Une heuristique traduit le plus souvent une intuition qui n’est pas nécessairement soutenue par des arguments formels.

Exemple avec les algorithmes de parcours de graphe

À ce stade, vous devriez être familier avec plusieurs algorithmes de parcours de graphe, tels que le BFS ou le DFS, dont le résultat est d’obtenir un arbre couvrant un graphe à partir d’un sommet donné.

Si vous y réfléchissez, utiliser un parcours plutôt qu’un autre peut être en soi une heuristique.

Par exemple, considérez le problème suivant : à partir d’une page Wikipédia, par exemple la page Wikipédia sur le problème du voyageur de commerce, nous voulons arriver à une autre page Wikipédia, par exemple la page Wikipédia sur le nombre 42, en suivant les liens hypertextes.

Question : faut-il utiliser un DFS ou un BFS ?

Il ne fait aucun doute que les deux méthodes obtiendront le résultat attendu, compte tenu de la très forte connectivité du graphe des hyperliens de Wikipédia, mais elles n’y parviendront certainement pas de la même manière.

Qu'est-ce qu'une bonne heuristique ?

Alors, qu’est-ce qu’une bonne heuristique ?

Une heuristique est le plus souvent inspirée par une intuition, et il n’est donc pas facile d’évaluer sa qualité à l’avance.

Une heuristique devrait avoir deux qualités importantes : fournir un gain et être limitée en termes de complexité. Examinons ces deux caractéristiques plus en détail.

Fournir un gain

Pour fournir un gain, une heuristique devrait améliorer les performances d’un algorithme selon un critère donné et par rapport à d’autres heuristiques.

Par exemple, imaginez que je veuille aller de cette salle de classe, le X jaune sur la carte, à la cantine, le X rouge sur la carte, en un nombre minimum d’étapes.

Une heuristique possible pour y arriver est de me déplacer dans ce que je sais être la direction générale de la cantine, en ignorant la présence de murs ou d’obstacles.

Cette heuristique aura probablement un meilleur résultat en général que si j’utilise une orientation aléatoire.

Mais dans certains cas, je pourrais me retrouver dans une impasse, auquel cas l’heuristique ne fournit pas de gain, et pire encore, ne fournit pas de solution.

Complexité limitée

En ce qui concerne la caractéristique de complexité limitée, si l’utilisation d’heuristiques est aussi coûteuse que l’exploration de toutes les possibilités, alors cela ne sert à rien, autant ne pas l’utiliser !

En utilisant le même exemple de moi trouvant mon chemin de cette salle de classe à la cantine, supposons que pour trouver mon chemin, je doive explorer tous les chemins possibles et compter le nombre d’étapes pour chacun d’eux. Je peux alors bien sûr choisir le chemin le plus court, mais comme j’ai dû explorer toutes les possibilités avant de le faire, j’aurai dû marcher beaucoup plus loin que si j’avais choisi une heuristique plus simple.

Évaluer la qualité

Pour évaluer la qualité d’une heuristique, il est généralement plus facile d’effectuer cette évaluation ex post. Cela signifie qu’un choix sur l’heuristique est fait, implémenté, puis testé sur un grand nombre d’instances de problème, et enfin, les résultats sont comparés aux résultats obtenus avec d’autres heuristiques.

Conclusion

Ceci conclut la leçon d’aujourd’hui sur les heuristiques. Dans la prochaine vidéo, vous apprendrez comment les heuristiques peuvent aider à fournir des solutions suffisamment bonnes au TSP. Au revoir !

Pour aller plus loin

2 — Heuristiques et solutions optimales

Comme indiqué précédemment, l’utilisation d’heuristiques peut conduire à trouver une solution correcte à un problème, mais pas nécessairement la solution optimale. C’est le cas par exemple de l’approche gloutonne, qui choisit itérativement des solutions localement optimales pour estimer un optimum global.

Néanmoins, utiliser une heuristique ne rend pas toujours une solution non optimale. Rappelez-vous par exemple l’algorithme de force brute avec backtracking étudié précédemment.

L’efficacité du backtracking dépend fortement de l’ordre dans lequel les branches de l’arbre de solutions sont explorées. Dans la session précédente, vous avez probablement choisi de visiter les sommets restants dans le méta-graphe comme ils apparaissent dans votre structure de méta-graphe ainsi :

​
def solve_tsp (graph, source):
    ...
    for vertex in graph.get_neighbors(current_vertex):
        if vertex not in current_visited_vertices:
            # Explore this branch
    ...

Cependant, utiliser une heuristique pour encoder une intuition sur quel voisin devrait être exploré en premier peut être une bonne idée, car (si c’est une bonne heuristique) cela pourrait conduire à l’exploration rapide de chemins courts, conduisant ainsi à l’élagage de nombreuses branches.

Le code partiel suivant est une solution possible, dans laquelle nous proposons d’utiliser un tas min, qui contiendra tous les voisins, avec une valeur associée correspondant au score donné par l’heuristique. Puisque c’est un tas min, plus le score est bas, meilleure est la qualité du voisin :

​
def heuristic (neighbor, ...):
    # Return a score for the neighbor to evaluate
    # In this example, the lower the score, the better, but you could adapt the code to change this
    ...
    return XXX

def evaluate_neighbors (neighbors, ...):
    # Here, we use our heuristic to give a score to all candidate neighbors
    # Then, we use these scores to fill a min heap
    scores = []
    for neighbor in neighbors:
        score = heuristic(neighbor, ...)
        heapq.heappush(scores, (score, neighbor))
    return scores

def solve_tsp (graph, source) :
    ...
    non_visited_neighbors = [neighbor for neighbor in graph.get_neighbors(current_vertex) if neighbor not in explored_vertices]
    scores = evaluate_neighbors(non_visited_neighbors, ...)
    while len(scores) > 0 :
        best_score, best_neighbor = heapq.heappop(scores)
        # Explore this branch first
    ...

Vous pouvez par exemple essayer de choisir comme heuristique de retourner un score qui est la distance entre le sommet exploré et le voisin candidat, c’est-à-dire, le poids dans le méta-graphe.

3 — Méta-heuristiques

Le préfixe “méta” indique que le mot auquel il est associé est placé à un niveau d’abstraction supérieur. Dans ce cas, une méta-heuristique est une heuristique qui sera elle-même utilisée pour trouver des heuristiques pour résoudre un problème.

Les méta-heuristiques permettent d’abstraire le problème de trouver les bonnes heuristiques, en considérant les heuristiques comme une solution à un problème d’optimisation, dont l’objectif est de maximiser la précision sur le problème étudié, tout en limitant la complexité. Ainsi, une méta-heuristique est un algorithme qui va parcourir l’espace des heuristiques possibles, et en choisir une qui sera jugée plus optimale que les autres selon certains critères (d’où la partie heuristique dans le mot).

Les méta-heuristiques ignorent complètement le problème étudié, considérant que l’heuristique recherchée n’est qu’une fonction qui doit être optimisée pour minimiser un critère. Ainsi, la même méta-heuristique peut être utilisée pour produire des heuristiques qui répondent à un très grand nombre de problèmes.

Parmi les méta-heuristiques les plus connues, on trouve les colonies de fourmis, les algorithmes génétiques, le recuit simulé, etc.

Pour aller encore plus loin