Activités pratiques 3
Duration2h30Présentation & objectifs
Voici quelques exercices pour vous faire manipuler des programmes simples et votre IDE.
Pendant cette activité, veuillez porter attention aux bonnes pratiques de programmation que vous avez étudiées précédemment. Ce sont de bons réflexes à acquérir rapidement.
Pour chaque exercice, nous vous demandons de montrer votre solution à un autre étudiant, afin qu’il puisse vous faire des remarques sur la lisibilité.
Le but de cette séance est de vous aider à maîtriser des notions importantes en informatique. Un assistant de programmation intelligent tel que GitHub Copilot sera capable de vous fournir une solution à ces exercices uniquement à partir d’un nom de fichier judicieusement choisi.
Pour comprendre et apprendre, vous ne devez pas utiliser ces outils pour l’instant.
Prendre le temps de réfléchir, de concevoir des algorithmes et de les coder vous-même est essentiel pour acquérir les compétences nécessaires.
Contenu de l’activité
1 — Correction de bugs syntaxiques
Le code suivant contient une erreur de syntaxe. Utilisez l’onglet Erreur de votre IDE pour trouver l’emplacement de l’erreur. Que dit-il ?
# The string to manipulate
s = "IMT Atlantique"
print(s)
# Loop to append to a new string
result = ""
for i j in range(len(s)):
result = s[i] + result
# Print the result
print("Reversed string:", result)Essayez de corriger l’erreur et exécutez à nouveau le code pour voir la différence !
2 — Correction de bugs sémantiques
Voici un code qui est syntaxiquement correct :
# Needed imports
import random
# Fill a list with 10 random numbers
numbers = []
for i in range(10):
numbers.append(random.randint(-50, 50))
# Let's do the following operation 50 times
for i in range(50):
# Divide each number by the subtraction of the two next numbers in the list
for j in range(len(numbers) - 2):
numbers[j] /= numbers[j + 1] - numbers[j + 2]
# Print the final list
print("Final list", numbers)Cependant, lors de son exécution, on obtient la sortie suivante :
Traceback (most recent call last):
File "session_1.py", line 14, in <module>
numbers[j] /= numbers[j + 1] - numbers[j + 2]
ZeroDivisionError: float division by zeroUtilisez la commande print pour trouver la source de l’erreur.
C’est-à-dire, ajoutez quelques print là où c’est pertinent pour comprendre ce qui mène à l’erreur.
Puis exécutez le code et essayez d’analyser pourquoi cela arrive.
3 — Programmation pas à pas
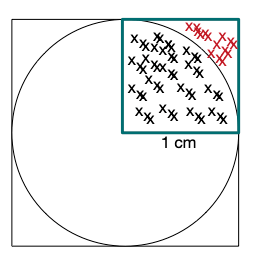
Vous allez implémenter une stratégie de Monte Carlo pour estimer la valeur de $\pi$. Le principe illustré dans la figure ci-dessous est de générer pseudo-aléatoirement les coordonnées cartésiennes de points situés dans le sous-espace unité, le carré cyan foncé. Considérant $n$ points pseudo-aléatoires générés, le rapport entre le nombre de points situés dans le quart supérieur droit du disque et le nombre total de points générés est une estimation de $\frac{\pi}{4}$.
Pour déterminer si un point est dans le quart supérieur droit du disque, il suffit de calculer sa distance euclidienne à l’origine. Si cette distance est inférieure à 1, il est dans le disque. Pour rappel, pour un point dont les coordonnées sont $(x,y)$, la distance à l’origine se calcule comme suit : $\sqrt{x^2 + y^2}$.
3.1 — Récupérez vos outils
Pour estimer $\pi$, vous avez besoin de quelques outils de programmation :
-
Un générateur de nombres aléatoires, et une méthode de ce générateur pour obtenir un nombre dans l’intervalle $[0, 1]$. Trouvez la méthode correcte dans la documentation du
module random. -
Une méthode pour calculer la racine carrée d’une valeur. Trouvez la méthode correcte dans la documentation du
module math.
Vous demanderez via une invite le nombre de points à générer (la valeur à affecter à $n$).
Pour ce faire, utilisez la fonction intégrée input.
Suivons quelques étapes pour obtenir un programme fonctionnel.
3.2 — Découpez votre algorithme en morceaux
Un code source complet est toujours écrit pas à pas, et chaque étape testée. C’est clairement la meilleure et la seule façon d’atteindre efficacement l’objectif. Alors, selon vous, que devons-nous faire ?
Implémentez cet algorithme étape par étape, et utilisez l’instruction print pour vérifier que chaque étape semble correcte.
En faisant varier la valeur de $n$, observez la précision de l’estimation de $\pi$ obtenue.
4 — Un problème classique de tri
Trier un tableau (ou une liste) de valeurs selon une relation d’ordre est un problème algorithmique très classique. Il est souvent utilisé pour découvrir empiriquement des concepts théoriques tels que la terminaison, la complexité, etc.
4.1 — Deux variantes de la stratégie de tri par sélection
L’algorithme de tri par sélection est très facile à comprendre (voici une explication avec musique et gestes). Considérez que vous avez un jeu de cartes non triées dans votre main droite et que vous construisez progressivement une permutation triée de ces cartes dans votre main gauche. La stratégie du tri par sélection consiste d’abord à sélectionner la carte ayant la plus petite valeur dans votre main droite et à la placer en première position dans votre main gauche. Vous faites ensuite de même avec la carte ayant la deuxième plus petite valeur, et ainsi de suite.
Identifiez les différentes étapes pour finalement avoir un programme qui génère un tableau de taille N (une constante choisie) composé de valeurs générées aléatoirement, puis trie ce tableau par sélection et vérifie que le tableau est bien trié.
Puis écrivez un programme qui effectue ce tri.
Une fois le programme prêt, écrivez une étape supplémentaire pour vérifier que le tableau est bien trié.
Testez sa correction en essayant différentes valeurs pour N (impaires et paires).
De plus, assurez-vous que le programme gère plusieurs occurrences des mêmes valeurs dans le tableau.
Une légère variation de l’algorithme consiste à positionner la plus petite et la plus grande valeur en même temps, la deuxième plus petite et la deuxième plus grande, etc. Implémentez cette stratégie dans un nouveau script.
4.2 — Comparaison empirique de leur efficacité
Pour chacune des stratégies de tri que vous avez développées dans la section précédente, assurez-vous de créer un script dédié.
Dans la suite, nous supposons que le premier s’appelle selection_sort_min.py, et le second selection_sort_min_max.py.
Puis, adaptez les deux scripts comme suit :
-
Le seul
printqu’ils doivent faire est le temps écoulé pour trier la liste, c’est-à-direprint(stop - start)dans les corrections ci-dessus (sans aucun autre texte). Supprimez tous les autres prints, ainsi que le test final pour vérifier si la liste est triée. -
Adaptez votre script pour récupérer la valeur de
Ndepuis le premier argument en ligne de commande, c’est-à-dire en utilisantsys.argv[1]. N’oubliez pas de la convertir en entier. -
Adaptez votre script pour récupérer la valeur de la graine aléatoire depuis le second argument en ligne de commande, c’est-à-dire en utilisant
sys.argv[2]. N’oubliez pas de la convertir en entier.
Maintenant, créez un nouveau script Python qui utilise la fonction intégrée sorted de Python.
Ci-dessous, nous supposons que ce script s’appelle built_in_sorted.py.
Il doit respecter les mêmes adaptations que les deux autres scripts ci-dessus, c’est-à-dire,
-
Être exécutable depuis la ligne de commande avec la commande suivante :
python <script_name> <N> <seed>python <script_name> <N> <seed>python3 <script_name> <N> <seed>python3 <script_name> <N> <seed> -
Afficher le temps total écoulé en résultat.
Cette fonction utilise un algorithme plus avancé appelé Powersort.
De plus, lors de l’appel à sorted, l’interpréteur appelle une version compilée de la fonction de tri en arrière-plan.
Elle peut donc être directement interprétée en code binaire par votre ordinateur, et est donc beaucoup plus rapide.
La plupart des fonctions intégrées de Python (et celles des bibliothèques) utilisent la même astuce, il est donc toujours préférable de les utiliser plutôt que de réinventer la roue. Moins vous écrivez de boucles, plus votre code Python sera rapide !
Maintenant, placez le script suivant dans le même répertoire que les fichiers que vous venez de créer.
N’oubliez pas d’adapter les noms de fichiers.
Ce script exécutera tous les autres scripts pour différentes tailles d’entrée, et créera un fichier .csv avec les temps moyens.
Il utilisera également la graine aléatoire pour s’assurer que tous les scripts sont comparés dans les mêmes conditions.
# Needed imports
import subprocess
import os
# Constants
SCRIPTS = ['selection_sort_min.py', 'selection_sort_min_max.py', 'built_in_sorted.py']
NB_TESTS_FOR_AVERAGE = 10
VALUES_OF_N = [10, 100, 1000, 10000]
OUTPUT_FILE_NAME = 'average_execution_times.csv'
PYTHON_EXECUTABLE = "python"
# We will write the average execution time for each script in a file
current_dir = os.path.dirname(__file__)
output_file = open(os.path.join(current_dir, OUTPUT_FILE_NAME), 'w', buffering=1)
# Loop over each script
for script in SCRIPTS:
# Loop over each value of N
results_for_n = []
for n in VALUES_OF_N:
# Loop over each test
execution_times = []
for seed in range(NB_TESTS_FOR_AVERAGE):
# Run the script
command = [PYTHON_EXECUTABLE, os.path.join(current_dir, script), str(n), str(seed)]
output = subprocess.run(command, capture_output=True, text=True)
result = float(output.stdout)
execution_times.append(result)
# Compute the average execution time
average_execution_time = sum(execution_times) / NB_TESTS_FOR_AVERAGE
results_for_n.append(average_execution_time)
# Write the results for the current script
output_file.write(script + ';')
output_file.write(';'.join([str(result) for result in results_for_n]))
output_file.write('\n')
# Close the file
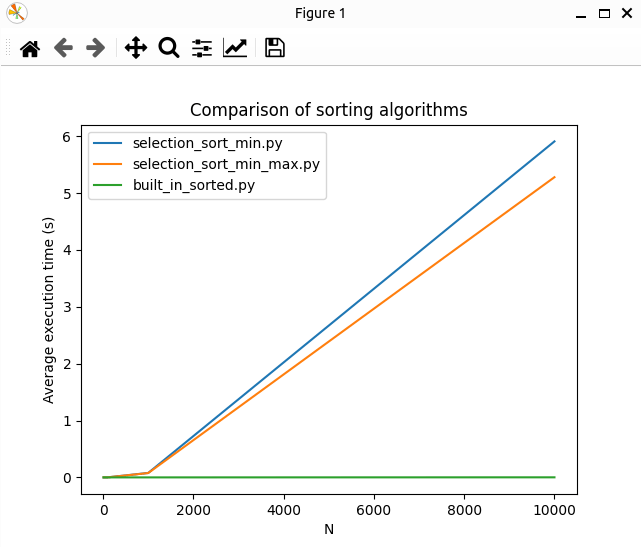
output_file.close()Puis, utilisez soit LibreOffice, Microsoft Office, ou tout logiciel équivalent, pour tracer, pour chaque script, le temps moyen en fonction de la taille de la liste.
Alternativement, vous pouvez aussi installer le paquet Python matplotlib pour créer cette courbe.
Voici un script pour le faire.
# Needed imports
import os
import matplotlib.pyplot as plt
# Constants
VALUES_OF_N = [10, 100, 1000, 10000]
CSV_FILE_NAME = 'average_execution_times.csv'
# Read the results from the file
current_dir = os.path.dirname(__file__)
results = {}
with open(os.path.join(current_dir, CSV_FILE_NAME), 'r') as file:
for line in file:
split_line = line.strip().split(';')
script = split_line[0]
times = [float(time) for time in split_line[1:]]
results[script] = times
# Plot the results
fig, ax = plt.subplots()
for script, times in results.items():
ax.plot(VALUES_OF_N, times, label=script)
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_xlabel("N")
ax.set_ylabel("Average execution time (s)")
ax.set_title("Comparison of sorting algorithms")
ax.legend()
plt.show()Pour aller plus loin
5 — Un problème classique de tri (encore)
Concevez un algorithme basé sur des comparaisons de tri qui satisfait l’invariant suivant :
Après
iitérations de la boucle interne, lesiplus grandes valeurs de la listelde tailleNsont triées dans un ordre croissant dans la partie droite del.
À chaque itération, la première valeur du tableau (indice 0) est déplacée par échange avec ses voisins vers la droite jusqu’à ce qu’une valeur plus grande soit trouvée. Dans ce cas, c’est cette valeur la plus grande qui est déplacée vers la partie droite du tableau. Une boucle interne est utilisée pour appliquer ce processus jusqu’à ce qu’aucun échange ne puisse plus être effectué.
Écrivez votre script dans un nouveau fichier appelé bubble_sort.py.
Assurez-vous que votre algorithme fonctionne correctement, comme vous l’avez fait dans un exercice précédent.
Une légère amélioration peut certainement être appliquée à votre algorithme pour réduire le nombre d’échanges.
Essayez de trouver ce qui peut être amélioré et comparez les deux versions selon le temps qu’elles mettent à trier le même tableau.
Écrivez votre solution dans un nouveau fichier appelé bubble_sort_2.py.