Structures de données & Parcours de graphes
Temps de lecture20 minEn bref
Résumé de l’article
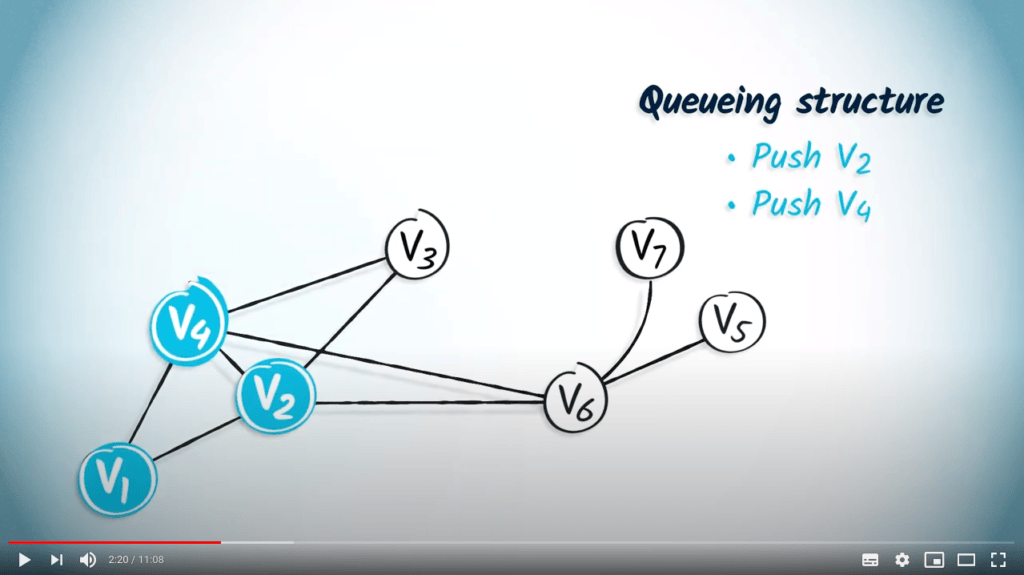
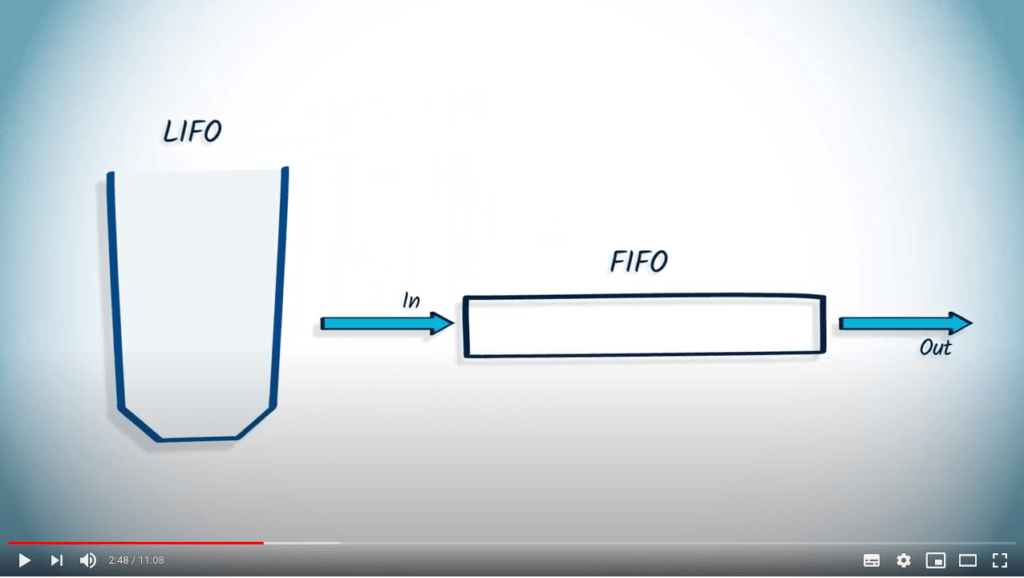
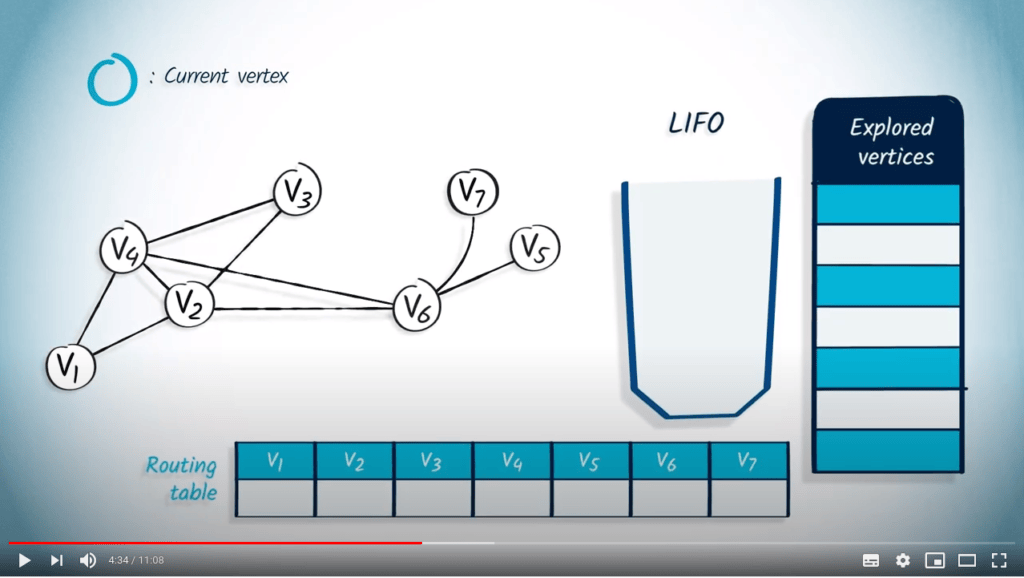
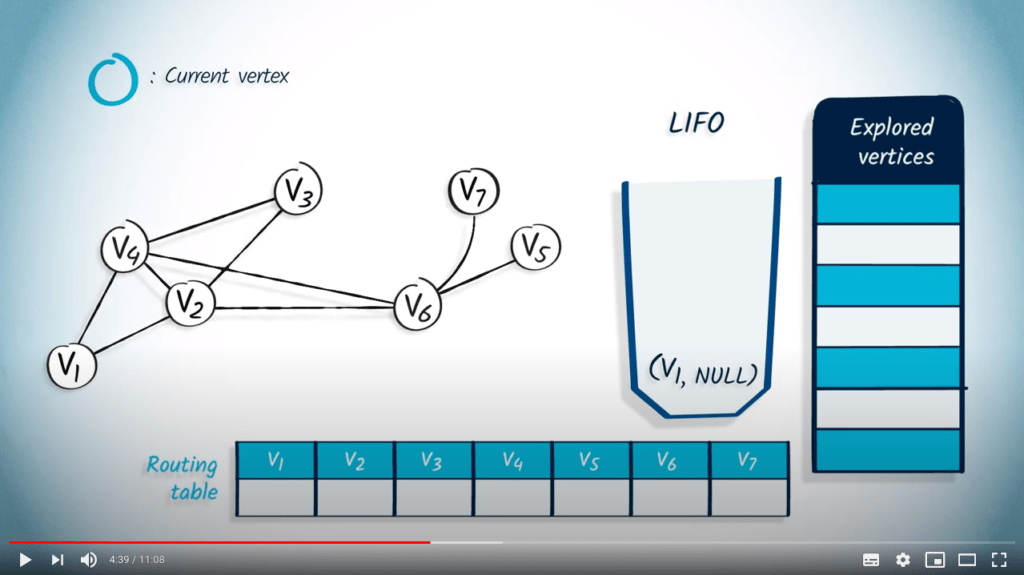
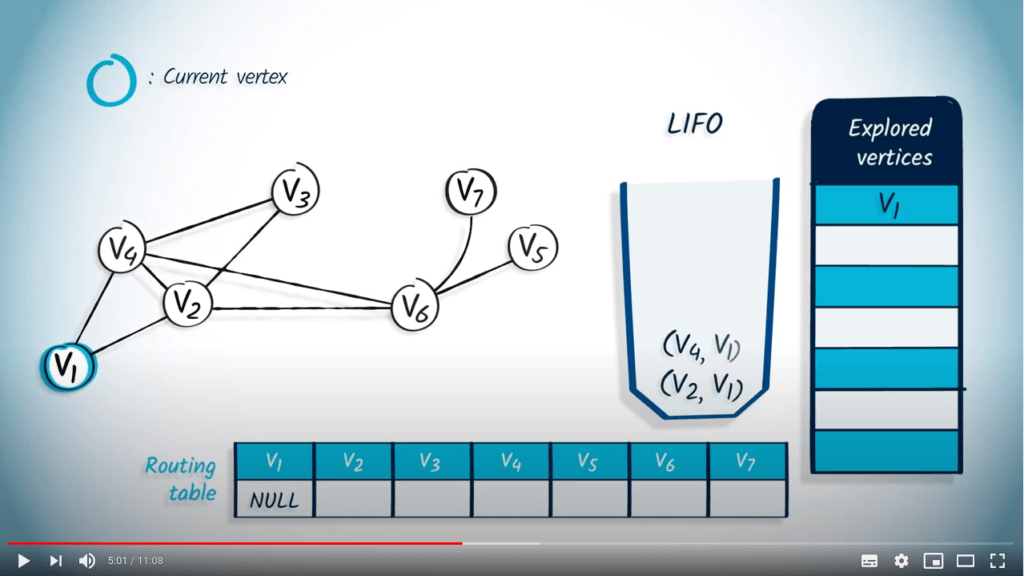
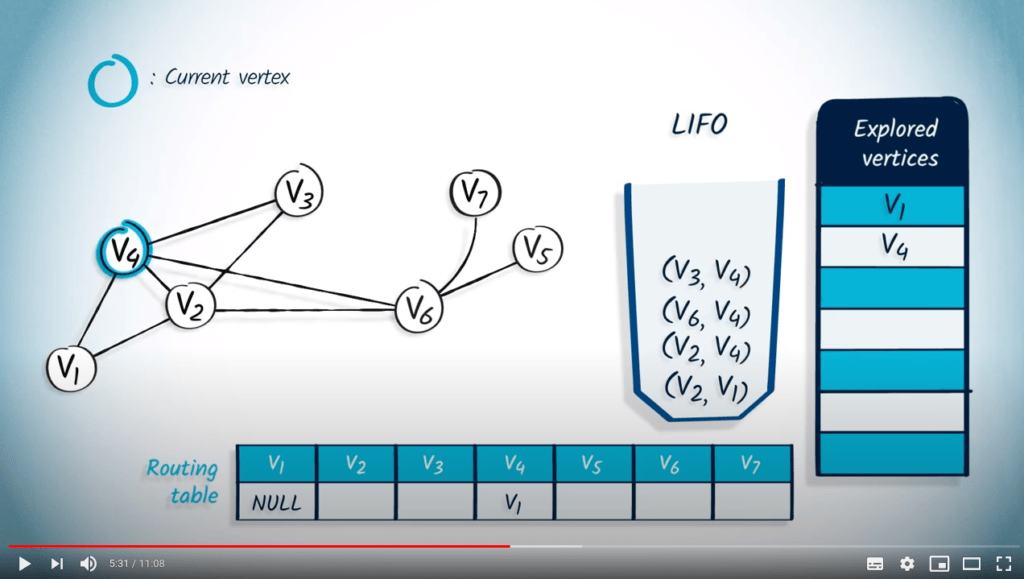
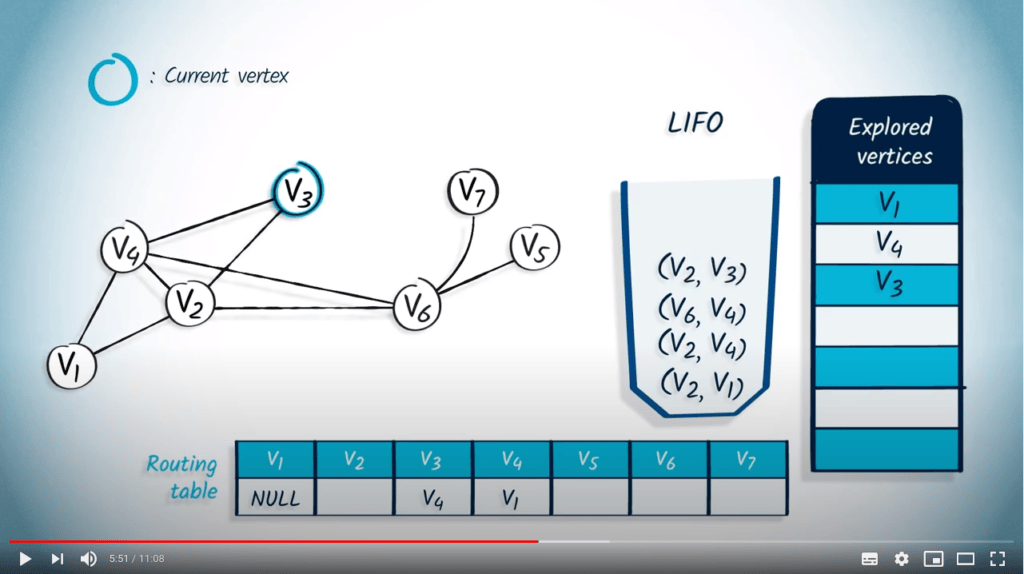
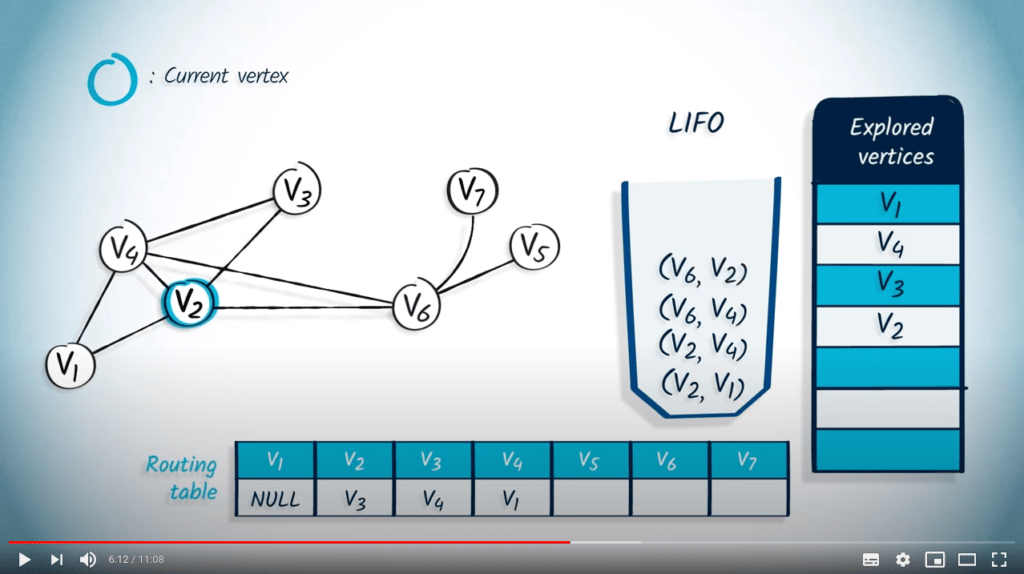
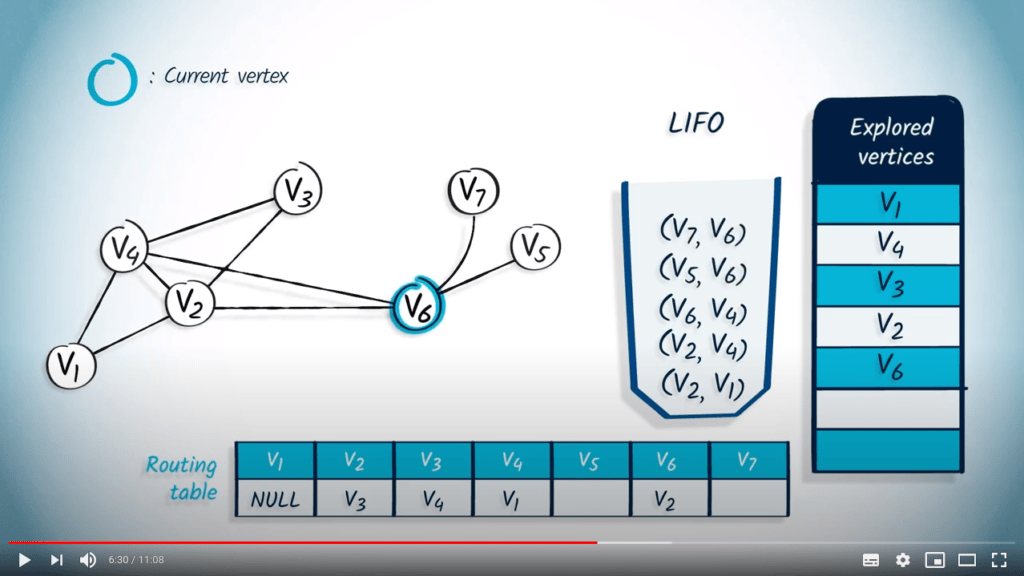
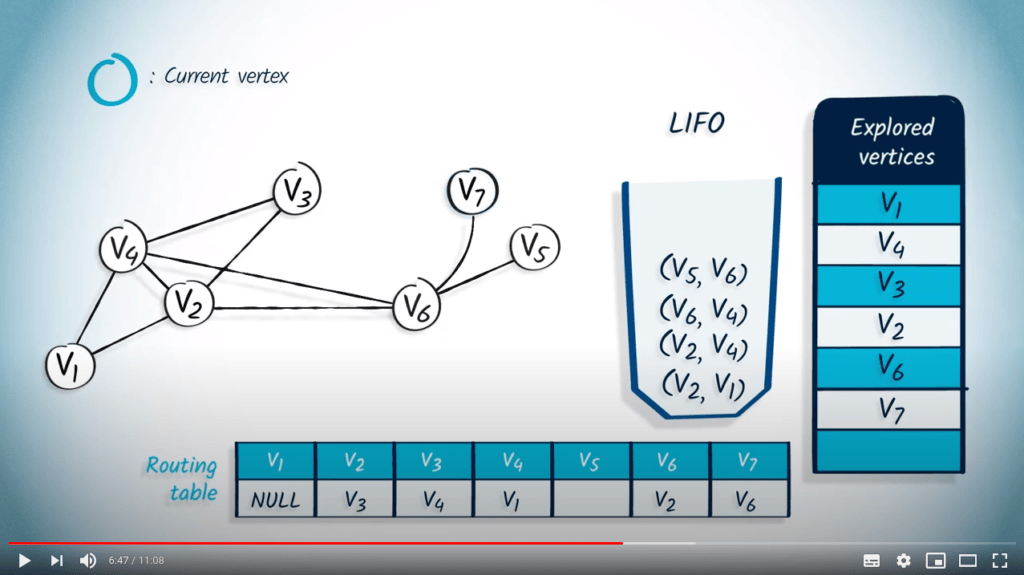
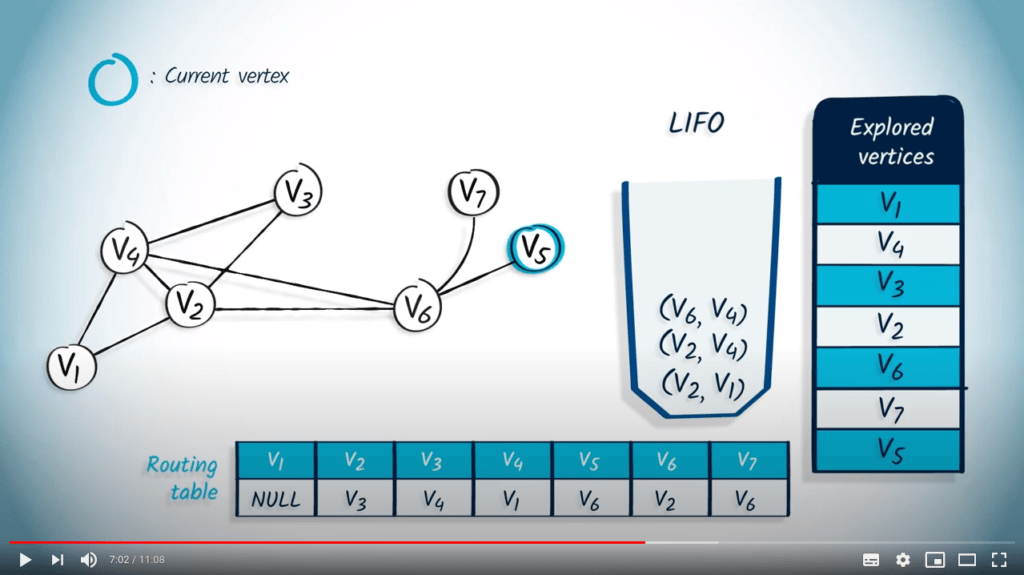
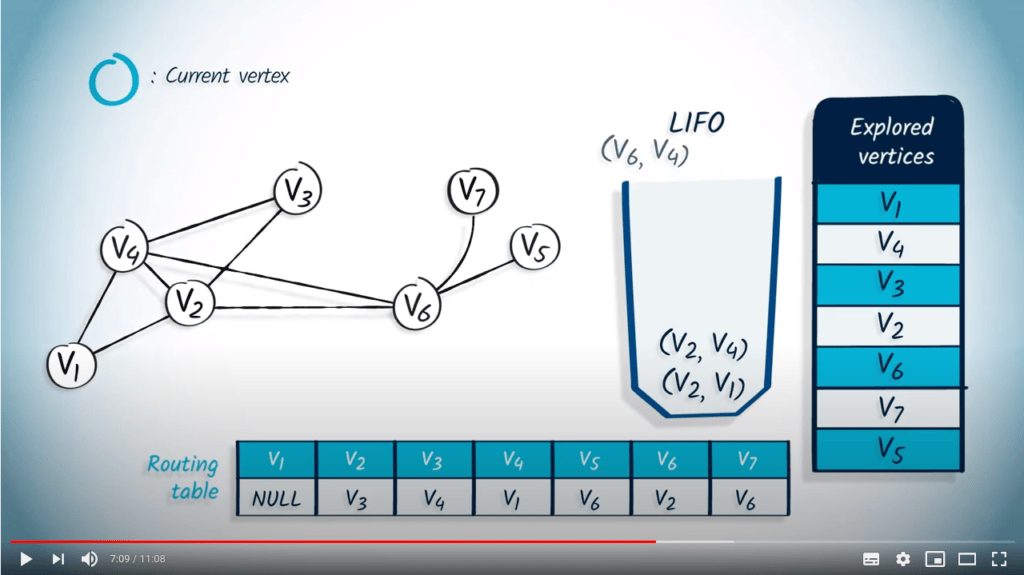
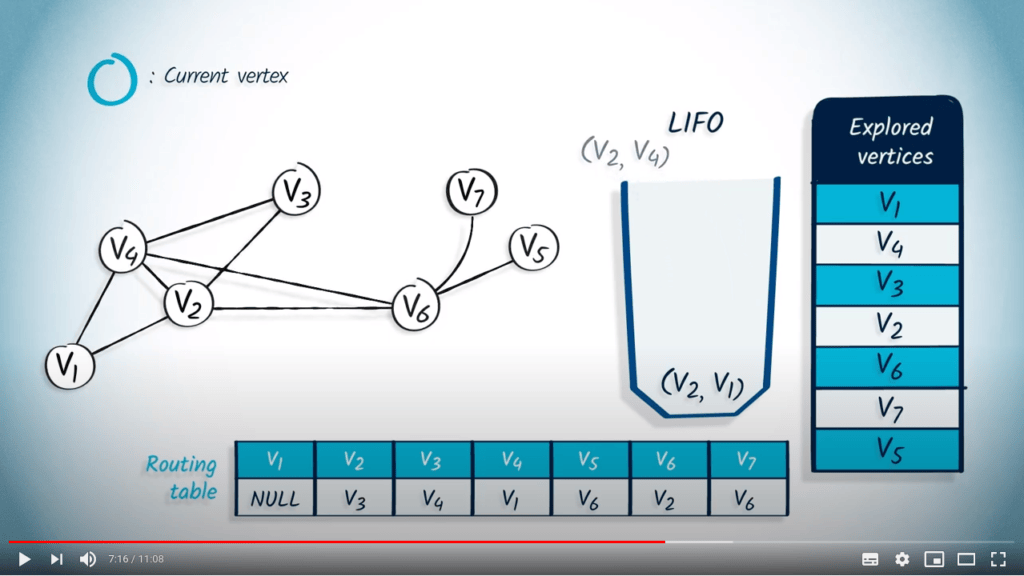
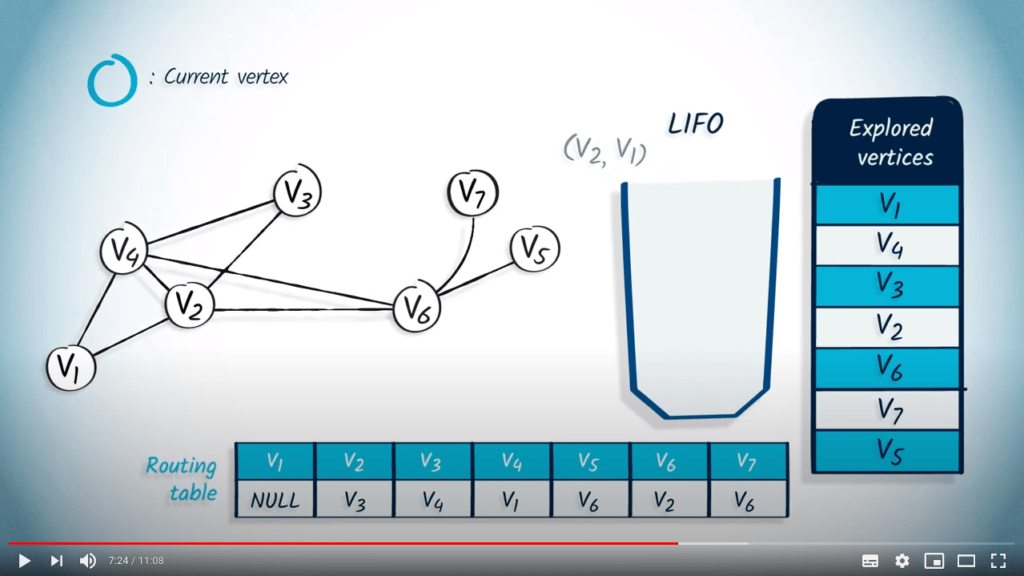
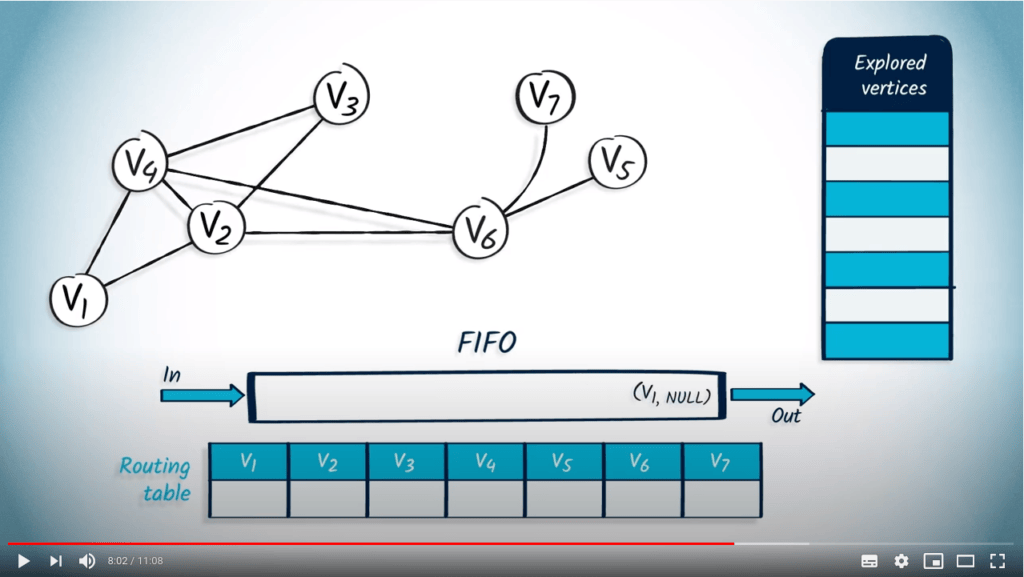
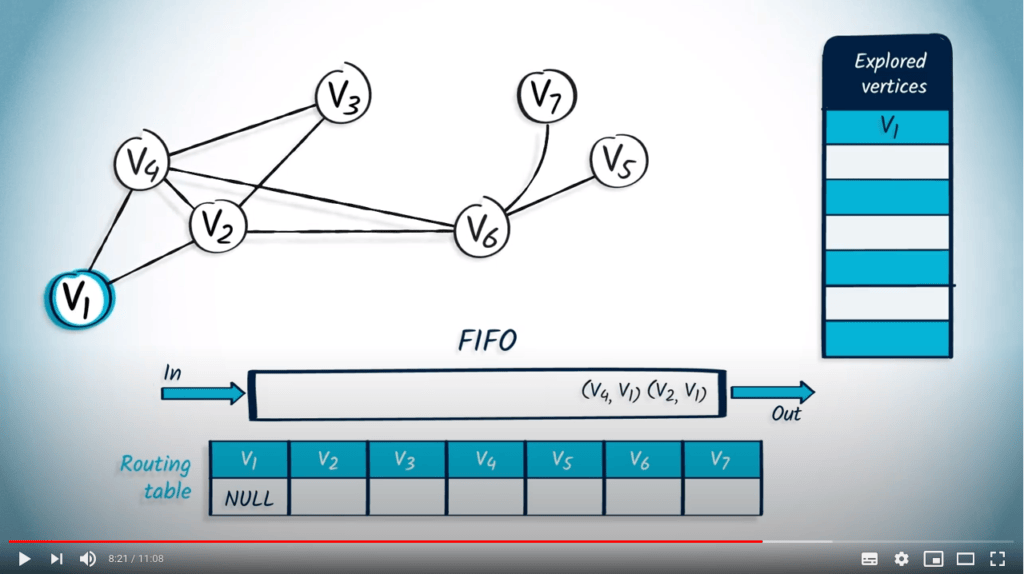
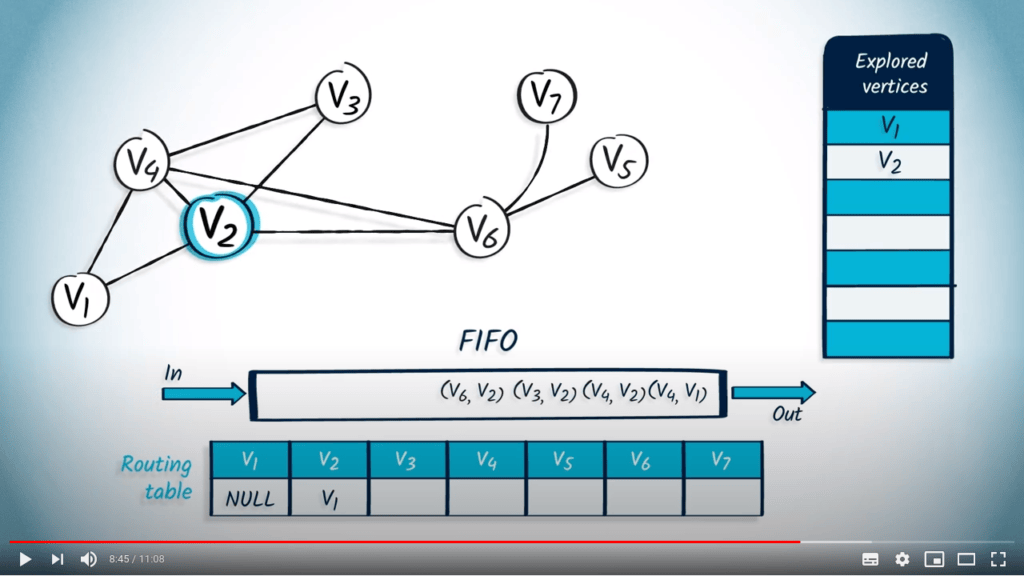
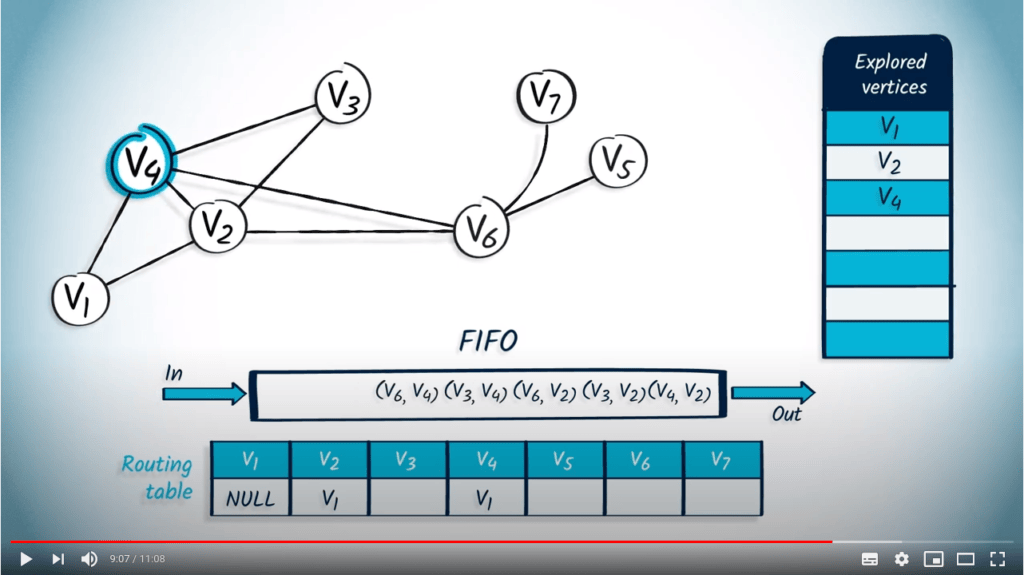
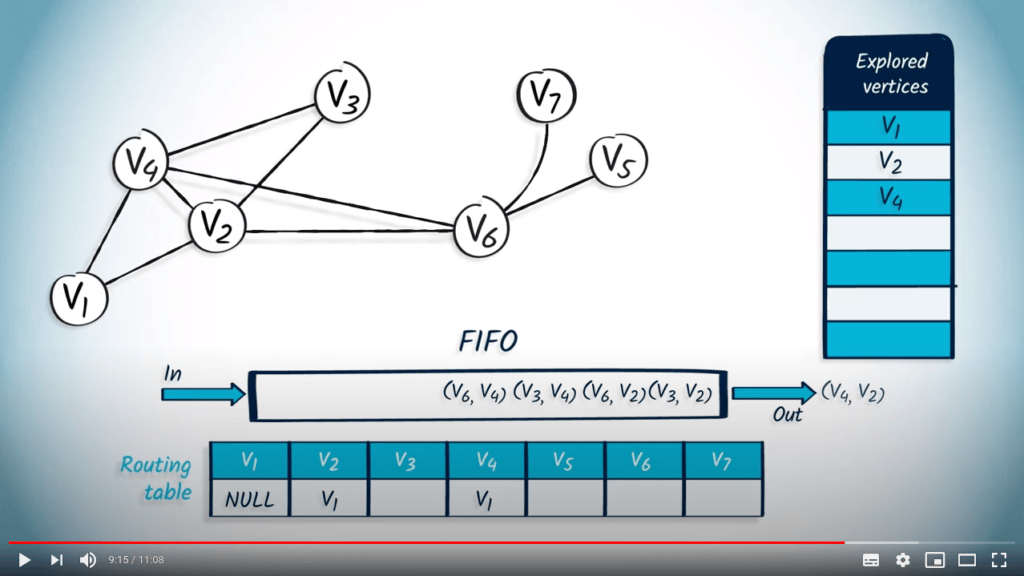
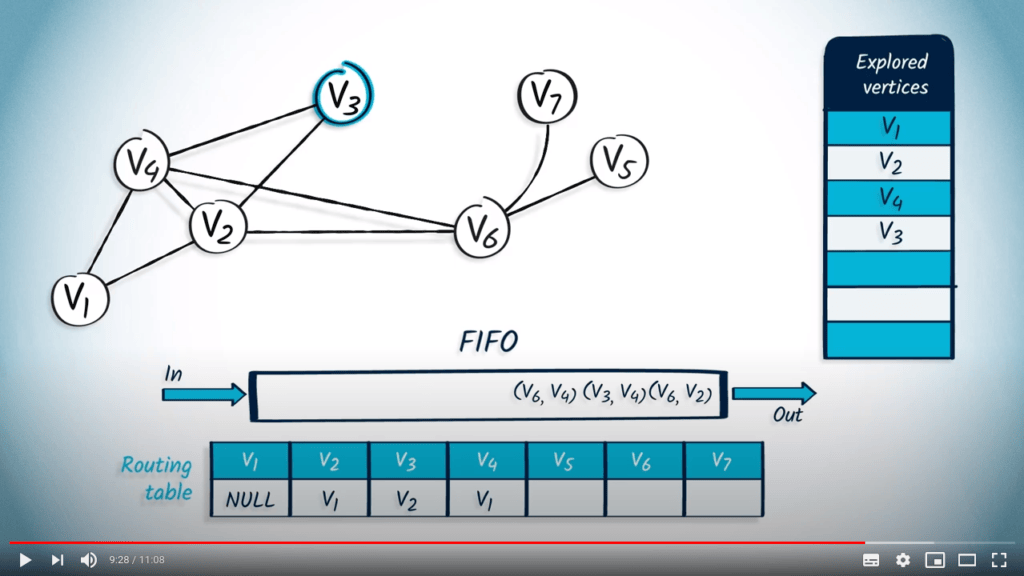
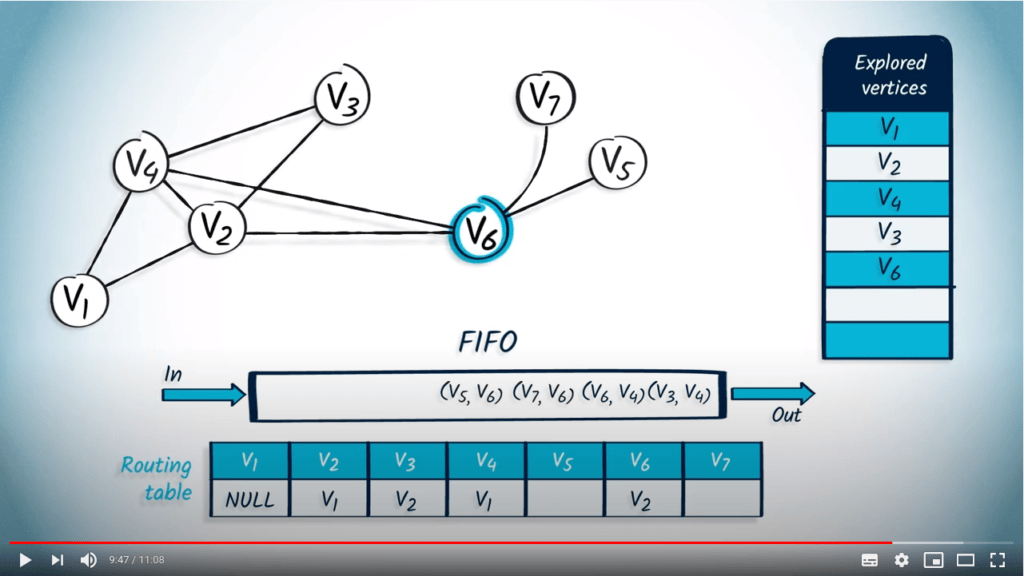
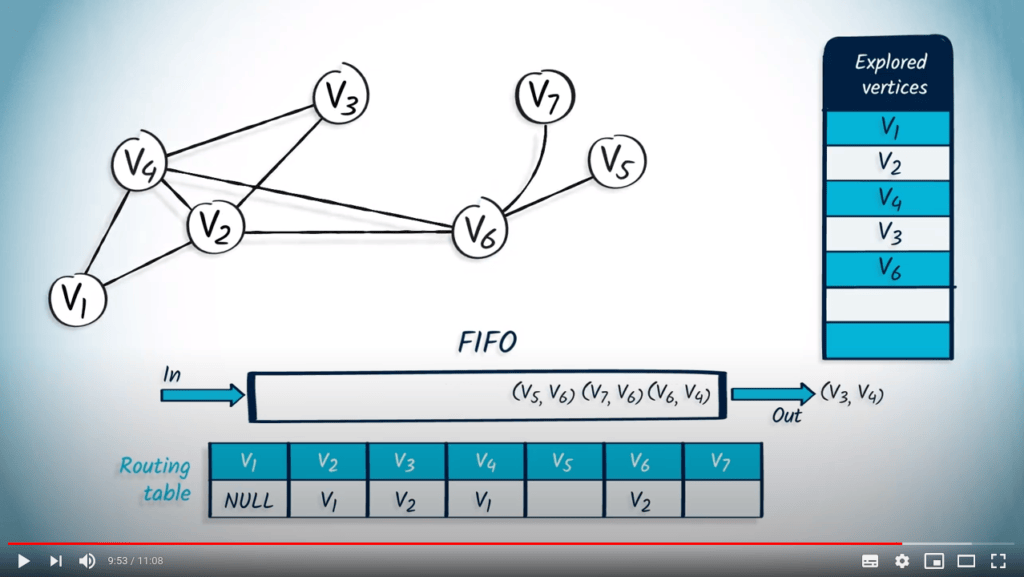
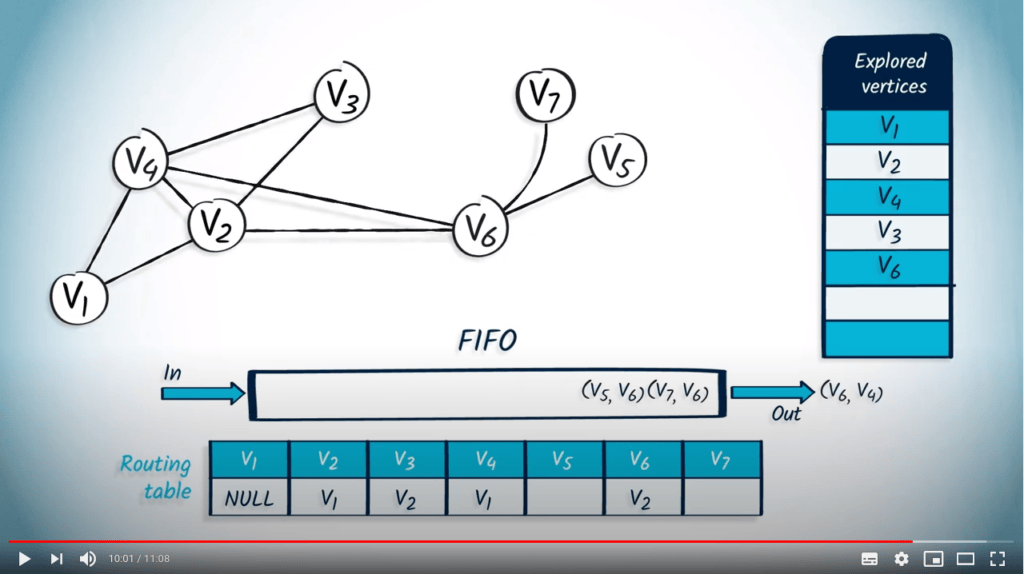
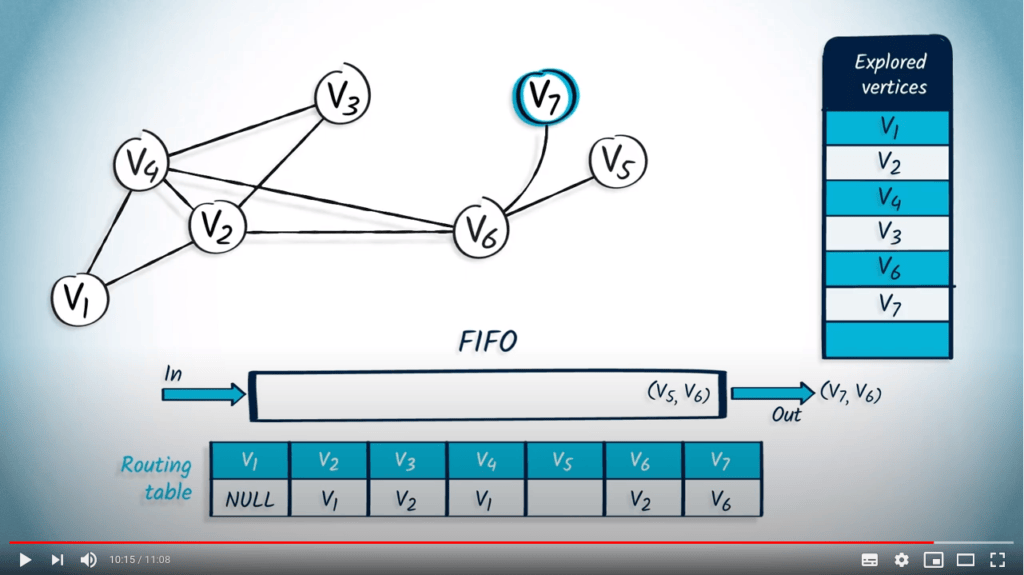
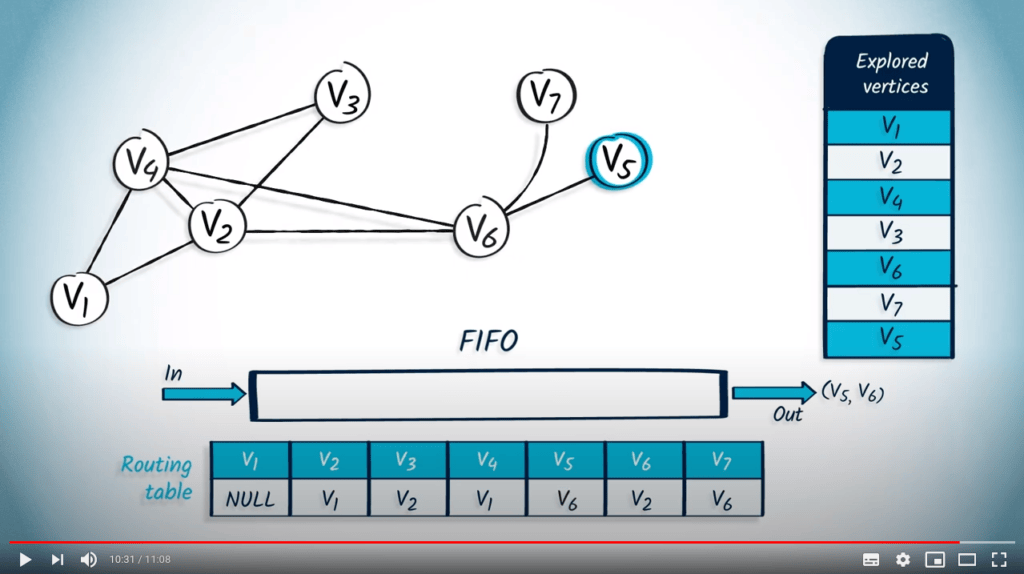
Dans cet article, vous découvrirez certaines structures de données courantes, et comment elles peuvent être utilisées pour façonner le comportement d’un algorithme de parcours. Vous découvrirez les structures LIFO (Last-In First-Out) et FIFO (First-In First-Out), qui définissent respectivement un DFS et un BFS.
Points clés
-
Les structures de données organisent l’information qu’on y stocke selon des règles spécifiques.
-
Certaines structures courantes sont les piles (stacks) et les files (queues).
-
Elles peuvent être utilisées pour façonner le comportement d’un parcours.
-
Le DFS et le BFS peuvent être vus comme un algorithme unique, paramétré avec une pile ou une file.
-
Ces structures de données trouvent des applications dans de nombreuses situations en informatique.
Contenu de l’article
1 — Vidéo
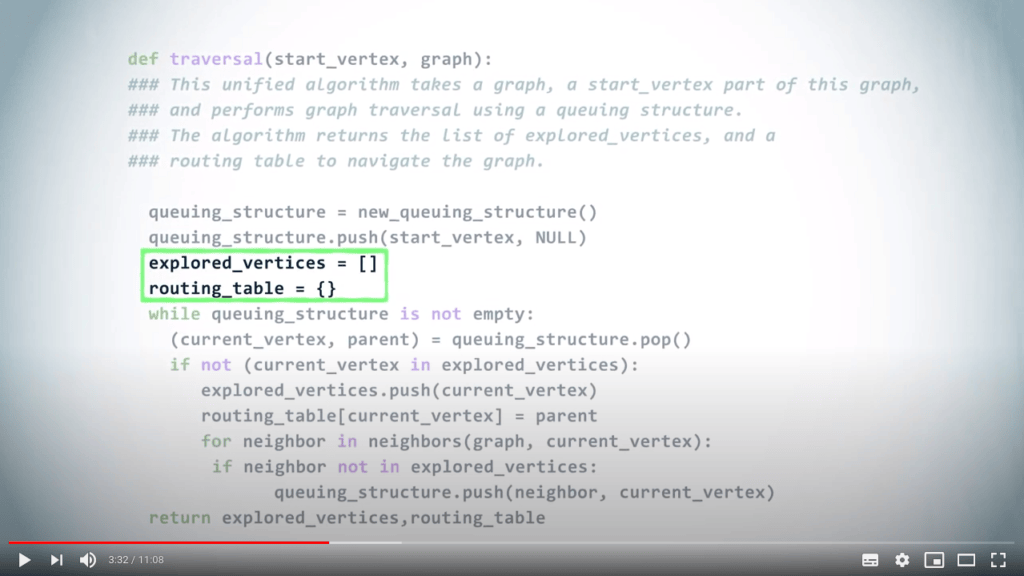
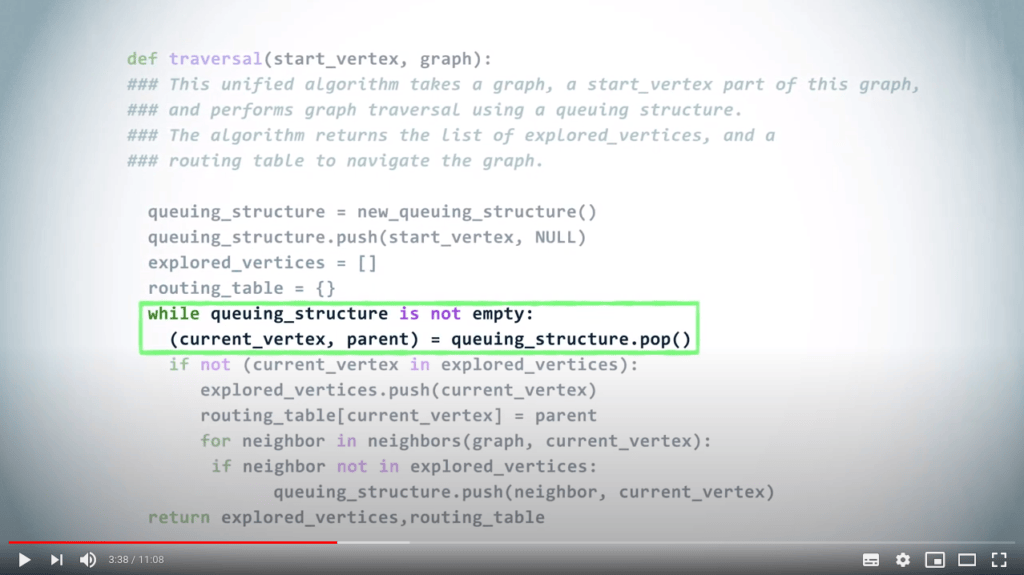
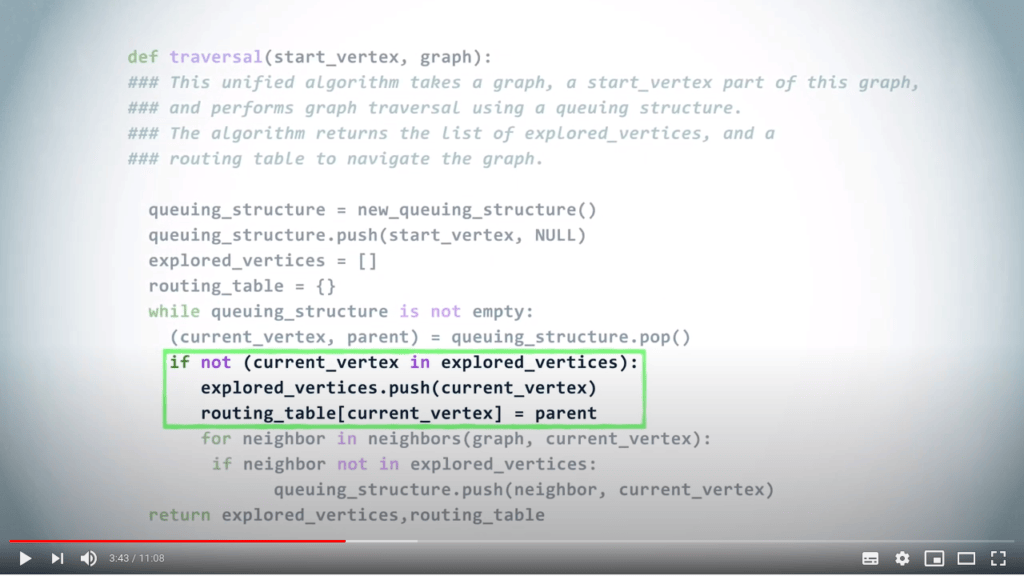
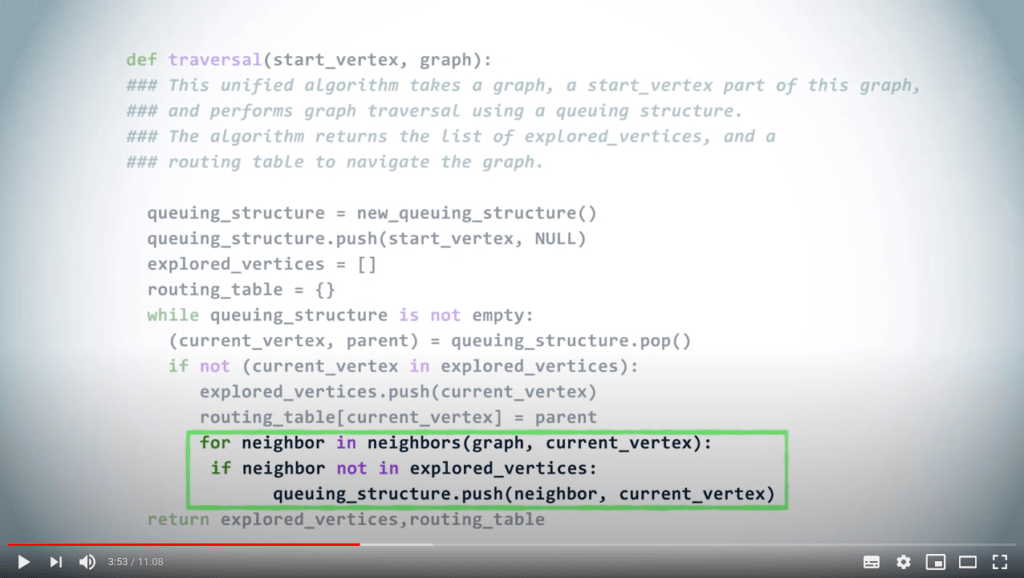
Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.
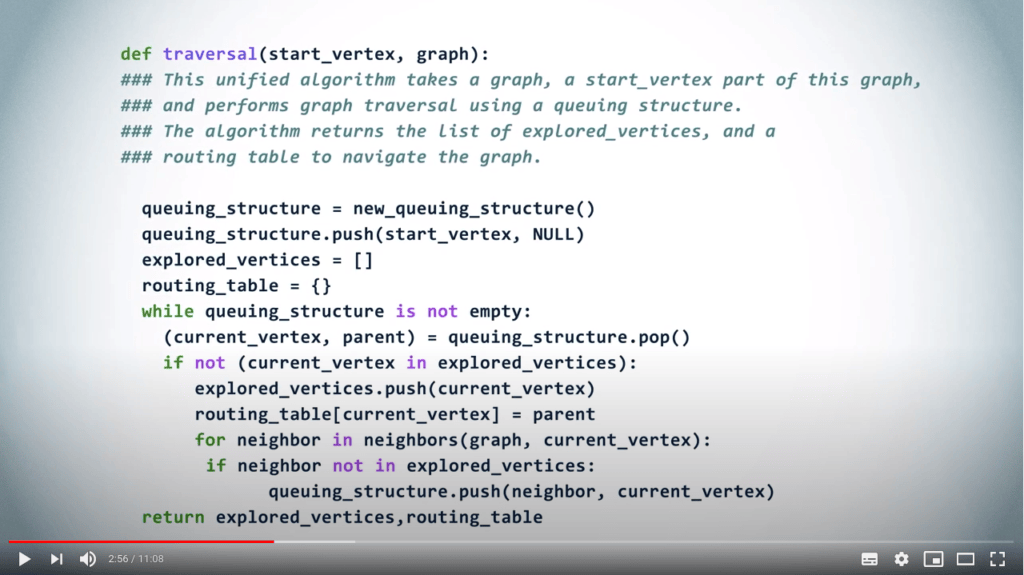
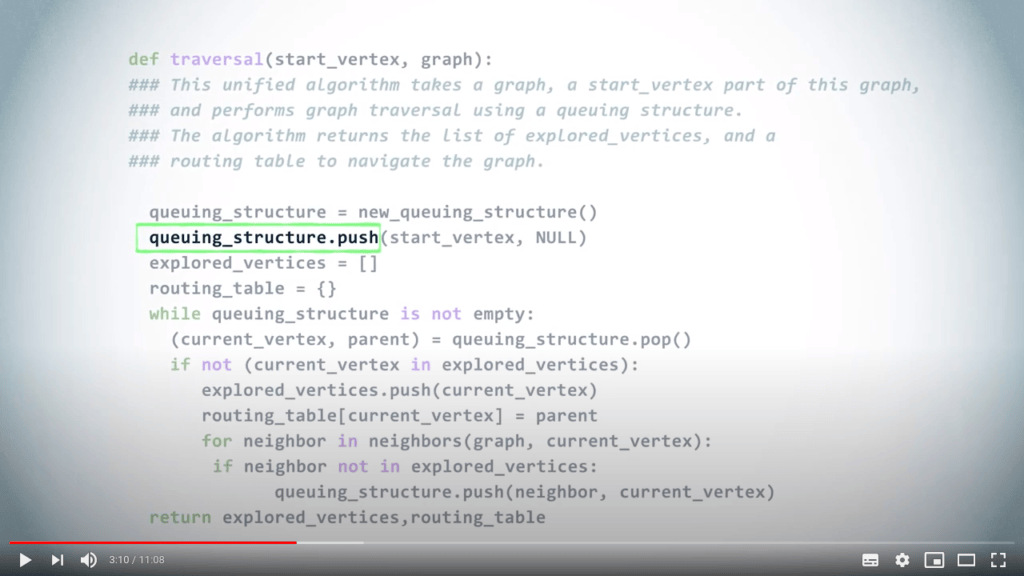
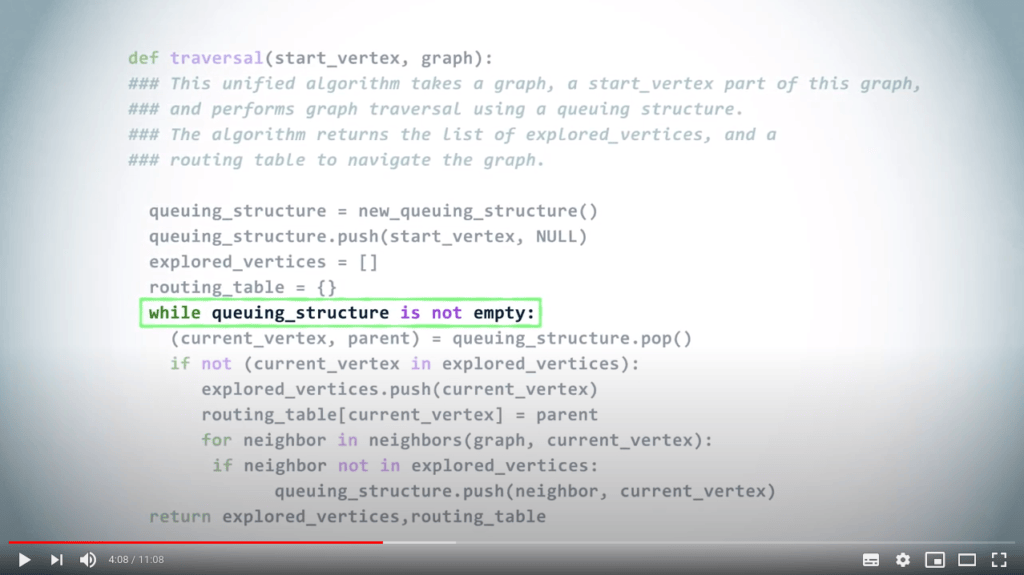
Certaines “codes” apparaissent dans cette vidéo. Veuillez garder à l’esprit que ce sont des pseudo-codes, c’est-à-dire qu’ils ne sont pas écrits dans un langage de programmation réel. Ça ressemble à du Python, mais ça n’est pas du Python !
Leur but est simplement de décrire les algorithmes sans se soucier des détails de la syntaxe d’un langage de programmation particulier. Vous devrez donc effectuer un peu de travail pour les rendre pleinement fonctionnels en Python si vous souhaitez les utiliser dans vos programmes.
Pour aller plus loin
2 — FIFOs et LIFOs en informatique
Pour illustrer l’importance de ces deux structures de données en informatique, nous présentons deux exemples de situations réelles dans lesquelles elles sont utilisées.
2.1 — Les FIFOs dans les systèmes de communication
Pour que deux personnes communiquent, elles doivent s’envoyer des messages. Et, pour que deux personnes se comprennent, elles doivent s’envoyer des messages dans un ordre logique. Vous comprendrez plus facilement la phrase “L’ordinateur permet à l’homme de faire des erreurs encore plus rapidement que n’importe quelle autre invention, à l’exception peut-être des armes à feu et de la téquila” que “Faire feu et peut-être rapidement n’importe l’ordinateur autre téquila l’exception des à de la armes encore invention permet des erreurs à l’homme de plus que quelle, à”.
Pour les machines, c’est pareil : l’ordre est important et doit être pris en compte. Certains modèles de communication (d’autres sont beaucoup plus complexes) utilisent des files pour cet objectif. Imaginez un modèle dans lequel nous avons un ordinateur $A$ qui écrit des mots dans une file, et un ordinateur $B$ qui les lit. Si l’ordinateur $A$ envoie les mots dans un ordre donné, alors $B$ les lira dans le même ordre (car le premier élément inséré dans une file est aussi le premier à en sortir), et la communication sera possible.
Vous vous demandez peut-être pourquoi passer par une FIFO et ne pas envoyer directement l’information ? L’avantage est que les ordinateurs $A$ et $B$ ne fonctionnent pas nécessairement à la même vitesse (qualité du processeur, carte réseau…). Ainsi, si l’ordinateur $A$ envoie des messages très rapidement à l’ordinateur $B$ (directement), ce dernier en manquera certains. Passer par une file permet de stocker les messages, dans l’ordre, pour éviter ces problèmes de synchronisation.
2.2 — Les LIFOs dans les langages de programmation
Lorsqu’un système d’exploitation exécute un programme, il lui alloue de la mémoire pour qu’il puisse effectuer ses calculs correctement. Cette mémoire est généralement divisée en deux zones : le tas (heap) qui stocke les données, et la pile (stack) qui permet (entre autres) d’appeler des fonctions dans les programmes.
Dans la plupart des langages de programmation, lorsqu’une fonction f(a, b) est appelée à un endroit du code, la séquence (simplifiée) suivante se produit :
- L’adresse de retour est empilée dans la pile.
Cela permettra de revenir juste après l’appel de
fune fois son exécution terminée. - L’argument
aest empilé dans la pile. - L’argument
best empilé dans la pile. - Le processeur est informé de traiter le code de
f. - On dépile un élément de la pile pour obtenir
b. - On dépile un élément de la pile pour obtenir
a. - Le code de
fest exécuté. - Une fois
fterminé, on dépile un élément de la pile pour obtenir l’adresse de retour et revenir à l’endroit oùfa été appelé. - Le processeur est informé de sauter à cette adresse.
Mais pourquoi utiliser une pile au lieu de variables pour transmettre ces informations ?
Eh bien, le processeur ne connaît pas les détails de f !
Il est possible que f utilise une autre fonction g, par exemple.
Si des variables étaient utilisées, l’adresse de retour de f serait écrasée par l’adresse de retour de g, et lorsque g serait terminé, il serait impossible de revenir au moment de l’appel de f.
Et pourquoi pas une FIFO alors ?
Ici encore, le problème se pose si f appelle une fonction g.
Comme l’adresse de retour de f est placée avant celle de g dans la file, lorsqu’il sera nécessaire de revenir de l’appel à g, le processeur obtiendra à la place l’adresse de retour de f (la plus ancienne dans la file) !
Nous n’exécuterons donc jamais le code de f situé après l’appel à g.
Pour aller encore plus loin
- Théorie des files d’attente.
Fournit des résultats supplémentaires sur les files (temps moyen avant d’être extrait, etc.) et a de nombreuses applications.