
C’est encore moi, bienvenue !
Je vois que vous êtes avide de concepts supplémentaires sur les algorithmes !
Dans cette leçon, nous allons examiner ce qu’on appelle la “complexité des algorithmes”.
Une introduction à la complexité des algorithmes
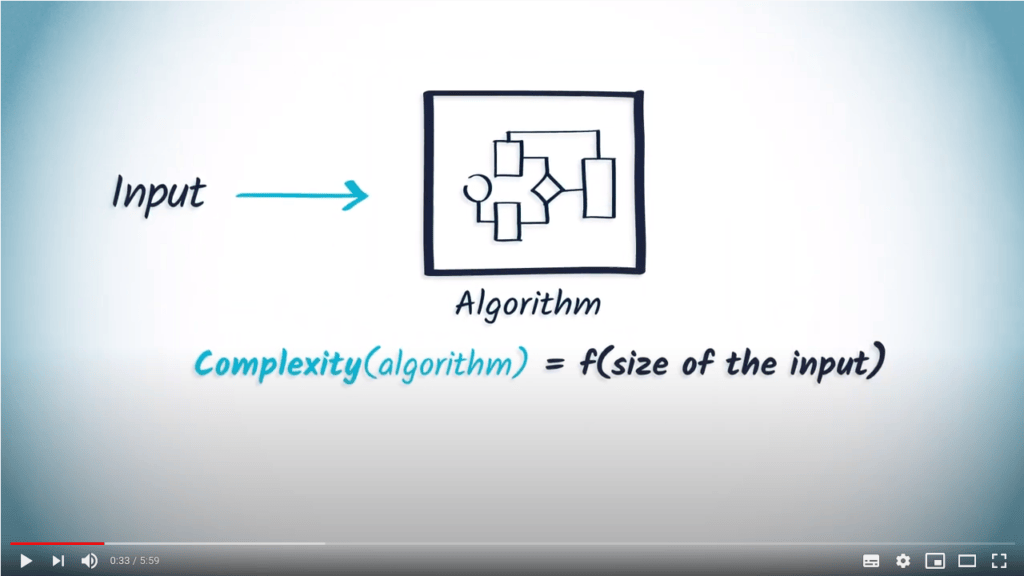
La complexité d’un algorithme est une mesure du nombre maximum d’opérations élémentaires nécessaires à son exécution, en fonction de la taille de l’entrée.
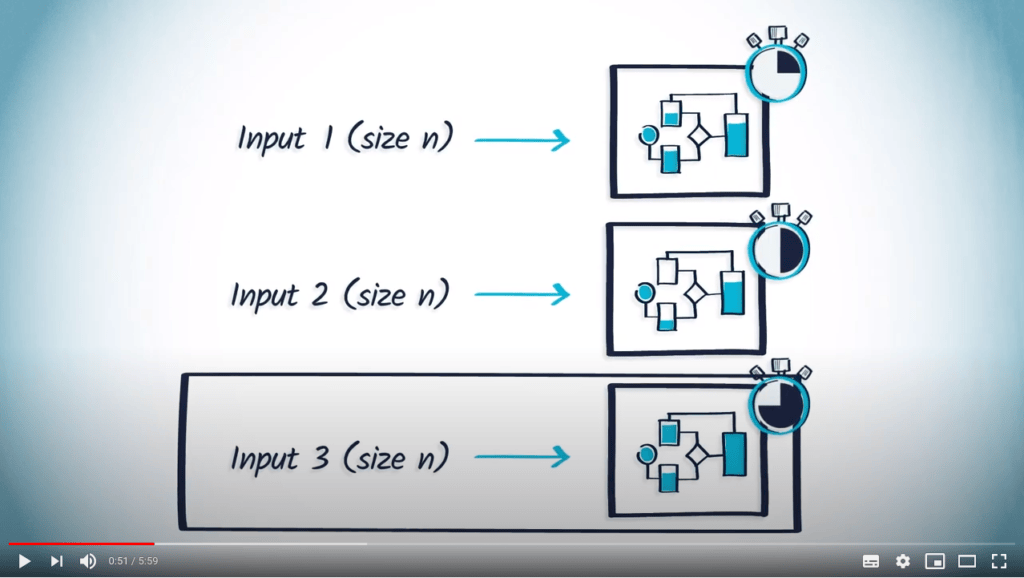
Il est évident que différentes entrées de même taille peuvent amener un algorithme à se comporter différemment.
Par conséquent, la fonction décrivant ses performances est généralement une borne supérieure des performances réelles, déterminée à partir des pires cas d’entrée pour l’algorithme.
Vous devez donc retenir ici que la complexité contient une notion de “pire cas”.

Cependant, pour bien comprendre le concept de complexité, nous devons définir deux choses plus précisément.
Prêts ?
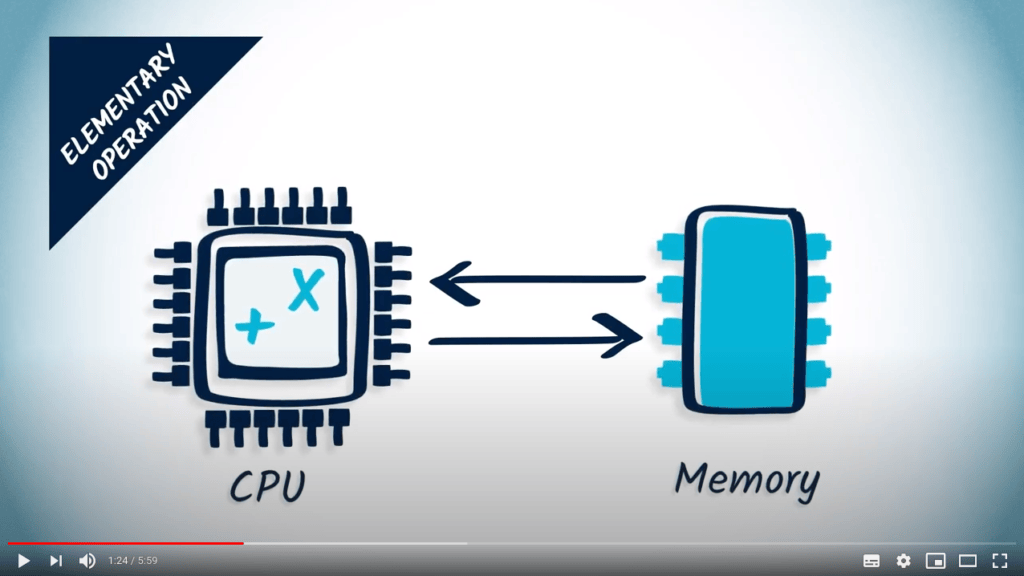
Une “opération élémentaire” est généralement une opération qui peut être exécutée en un temps très court par l’unité centrale de traitement, ou CPU, de l’ordinateur sur lequel l’algorithme est implémenté.
Par exemple, l’addition, la multiplication et l’accès à la mémoire sont considérés comme des opérations élémentaires.

Parfois, additionner ou multiplier des nombres peut être très coûteux en termes de temps.
Cela peut être vrai lorsqu’on additionne ou multiplie des nombres très grands, comme ceux utilisés dans certains algorithmes cryptographiques.
En d’autres termes, la définition des opérations élémentaires dépend de la tâche.
La deuxième chose à comprendre est que la taille de l’entrée dépend du contexte de l’algorithme.

Par exemple, si nous considérons l’addition de deux entiers, la taille serait le logarithme en base 2 du plus grand nombre, correspondant au nombre de bits utilisés pour le représenter en mémoire.
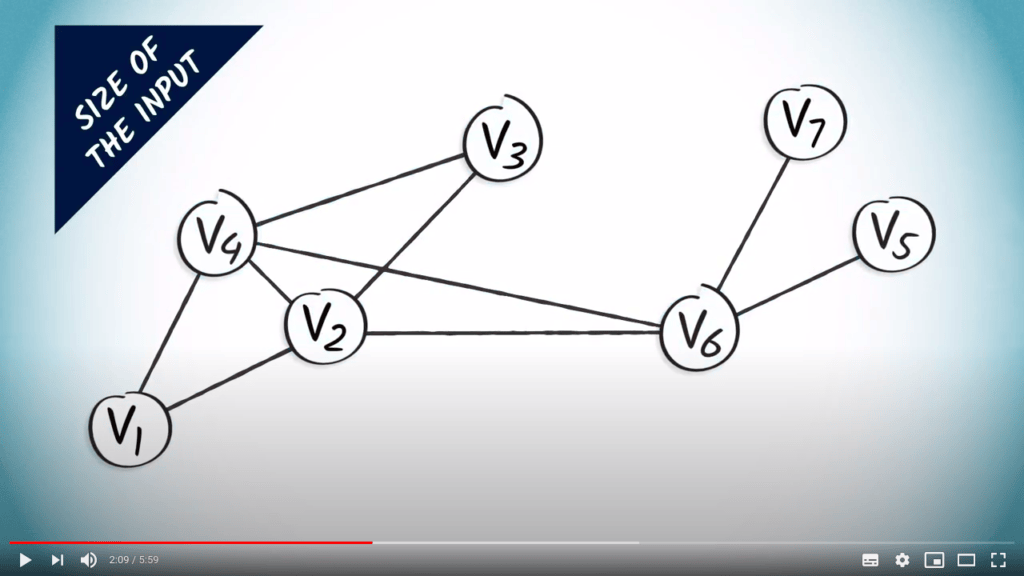
Dans le cas des algorithmes impliquant des graphes, la taille peut être le nombre d’arêtes ou de sommets.

Passons à la suite.
La complexité est généralement exprimée sous forme de “comportement asymptotique” en utilisant la notation “grand-O”.

Et pourquoi ?
Parce que connaître ce comportement asymptotique est souvent suffisant pour décider si un algorithme est suffisamment rapide, et il est souvent inutile d’avoir des estimations plus précises.
Le comportement asymptotique exprimé par la notation grand-O nous permet d’ignorer les constantes et les termes de faible ordre.
C’est parce que lorsque la taille du problème devient suffisamment grande, ces termes n’ont plus d’importance.
Notez que deux algorithmes peuvent avoir la même complexité en temps grand-O, même si l’un est toujours plus rapide que l’autre.

Par exemple, supposons que l’algorithme 1 nécessite $n^2$ temps, et que l’algorithme 2 nécessite $10 n^2+3n$ temps. Pour les deux algorithmes, la complexité est $O(n^2)$, mais l’algorithme 1 sera toujours plus rapide que l’algorithme 2 pour une même entrée.
Dans ce cas, les constantes et les termes de faible ordre comptent.
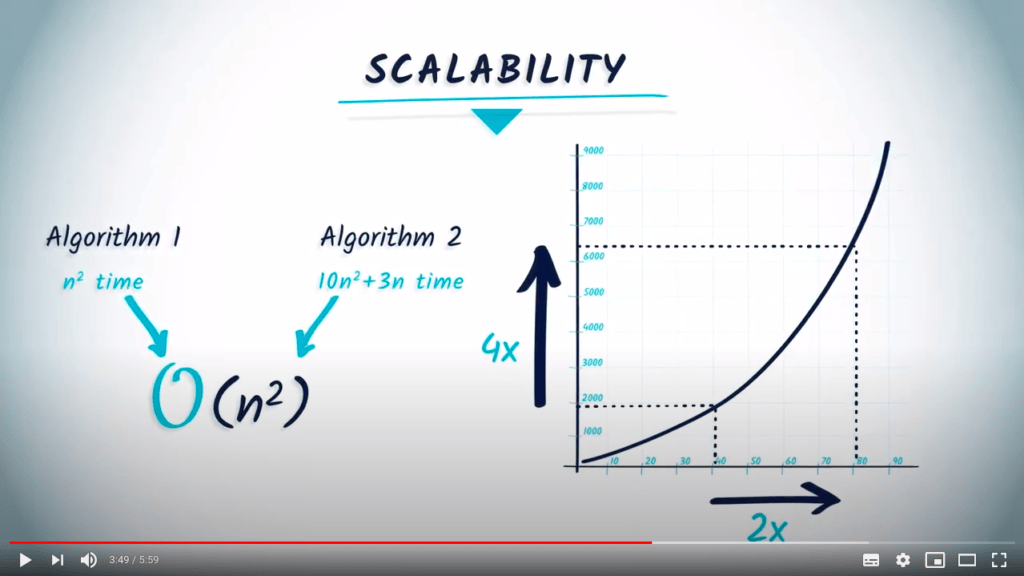
Cependant, les constantes n’ont pas d’importance pour la question de la scalabilité, qui examine comment le temps d’exécution de l’algorithme change en fonction de la taille du problème.
Bien qu’un algorithme nécessitant $n^2$ temps soit toujours plus rapide qu’un algorithme nécessitant $10n^2 +3n$ temps, pour les deux algorithmes, lorsque $n$ devient suffisamment grand et que la taille du problème double, le temps réel quadruple.

En général, les algorithmes considérés comme rapides sont ceux ayant une complexité linéaire, $O(n)$, ou ceux pour lesquels la complexité est $O(n \cdot log(n))$.
Les algorithmes dont la complexité est $O(n^k)$ pour $k \geq 2$ sont considérés comme ayant une complexité raisonnable, selon le domaine d’application.
Les algorithmes ayant au moins une complexité exponentielle sont rarement utilisés en pratique.
Complexité des algorithmes que nous avons vus jusqu'à présent

Mettons cela en contexte avec les algorithmes que nous avons vus jusqu’à présent.
Les algorithmes DFS et BFS examinent chacun des sommets d’un graphe une fois, et pour chaque sommet, ils considèrent tous ses voisins.

Par conséquent, leur complexité est de l’ordre du nombre d’arêtes dans le graphe, $O(|E|)$.

Concernant l’algorithme de Dijkstra, la complexité dépendra largement de l’implémentation du tas minimum.
En pratique, il est possible d’obtenir une complexité de $O(|E|+|V| \ln(|V|))$.
Cependant, nous ne démontrerons pas ce résultat ici.
Conclusion

Cela conclut la leçon d’aujourd’hui sur la complexité des algorithmes.
Comme vous l’avez peut-être deviné, la complexité est un outil important pour évaluer les performances d’un algorithme avant de commencer à l’implémenter.
Par exemple, imaginez que vous souhaitez implémenter une intelligence artificielle dans un jeu.
Comme la complexité en temps est directement liée au temps de calcul, et que le temps de calcul est directement lié au temps de réponse de votre intelligence artificielle, vous pouvez voir à quel point cette question est importante si vous souhaitez battre vos adversaires.
À la semaine prochaine, où vous apprendrez un problème très important en informatique : le problème du voyageur de commerce, ou TSP.
Malheureusement, nous verrons également que les algorithmes pour le résoudre sont très complexes.
Mais heureusement, cela ne signifie pas qu’ils sont compliqués à comprendre.












