Calculer les positions gagnantes dans un jeu
Temps de lecture20 minEn bref
Résumé de l’article
Dans cet article, nous vous expliquons comment trouver les positions gagnantes dans un jeu, c’est-à-dire, comment trouver des configurations qui mèneront sûrement à la victoire.
À retenir
-
Gagner un jeu consiste à atteindre une configuration de jeu où le jeu est gagné.
-
Plus largement, les régions gagnantes désignent des configurations à partir desquelles une configuration gagnante peut sûrement être atteinte.
-
Les régions gagnantes peuvent être construites en partant des configurations gagnantes.
-
Des algorithmes tels que Maximin peuvent être utilisés pour trouver une bonne stratégie dans un jeu.
Contenu de l’article
1 — Vidéo
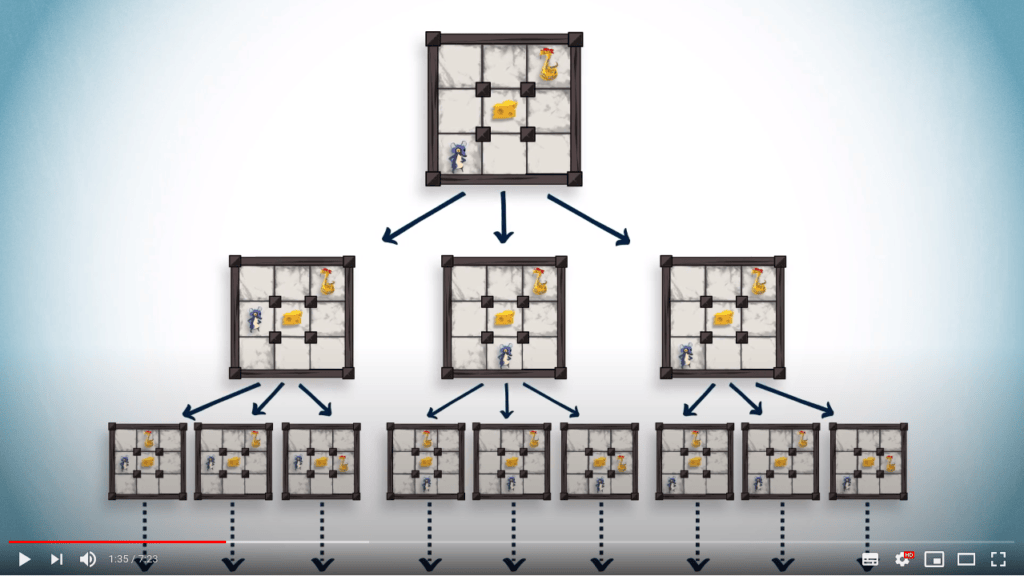
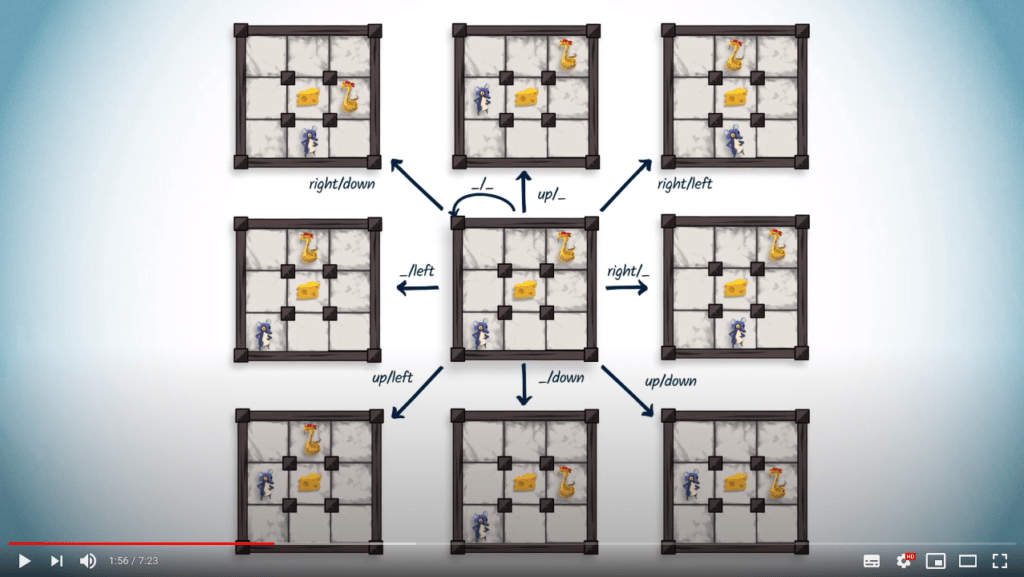
Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.
Pour aller plus loin
2 — L’algorithme maximin
En théorie des jeux (plus précisément dans les jeux à information complète et à somme nulle), l’algorithme maximin vise à trouver le meilleur coup à jouer à chaque étape, en supposant que l’adversaire jouera de manière optimale. L’objectif pour l’adversaire est donc de minimiser notre gain, tandis que le nôtre est de le maximiser.
Concrètement, l’idée principale de l’algorithme est de partir des feuilles de l’arbre des solutions, et de donner un score à chacune de ces feuilles, correspondant au gain qu’elle nous procure.
Ensuite, nous allons remonter l’arbre jusqu’à atteindre la racine, en alternant des minimisations des scores et des maximisations. Cette alternance modélise les choix soit du joueur, soit de l’adversaire.
2.1 — Exemple
Décrivons ce qui se passe sur un exemple, tiré de la page Wikipédia sur l’algorithme Minimax (minimax est juste le problème symétrique de maximin dans lequel nous voulons minimiser une fonction de perte plutôt que maximiser un gain) :
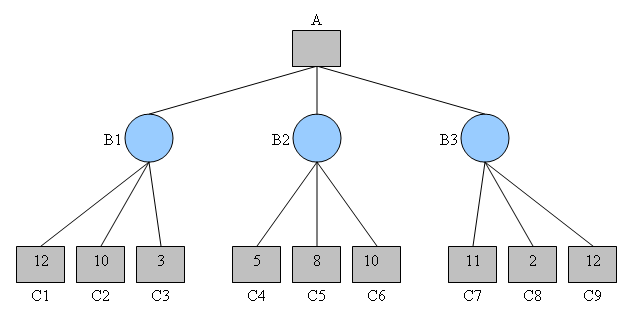
Ici, nous avons un arbre d’exécutions possibles d’un jeu, dans lequel les profondeurs modélisées par des carrés indiquent notre tour de jouer, et les cercles indiquent le tour de l’adversaire.
Pour chaque nœud cercle, l’adversaire essaiera de minimiser notre gain, en choisissant d’effectuer l’action qui mène au gain minimum pour nous. Par conséquent, l’algorithme minimax supposera les choix suivants :
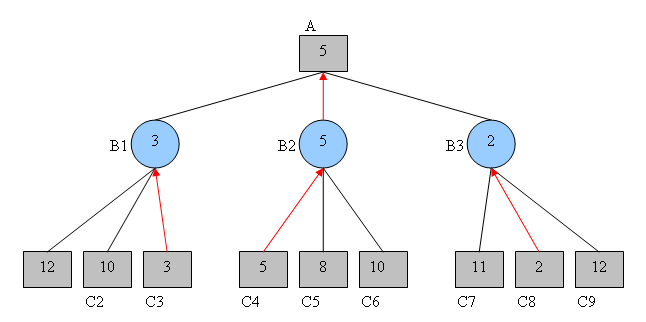
Ce que cela signifie maintenant, c’est que, si j’atteins l’état du jeu $B1$, l’adversaire jouera de sorte que notre gain total soit 3, obtenu à partir de l’état $C3$. Si nous faisons en sorte que le jeu aille à l’état $B2$, notre adversaire peut jouer de sorte que le gain soit 5 en imposant l’état $C4$. Enfin, si nous jouons pour atteindre la situation $B3$, l’adversaire peut jouer de sorte que le gain soit 2 en imposant l’état $C8$.
Le choix optimal pour nous est donc de maximiser le gain, et de jouer de sorte que nous atteignions l’état $B2$. En faisant ce choix, le meilleur gain que l’on peut espérer face à un adversaire optimal est 5 :
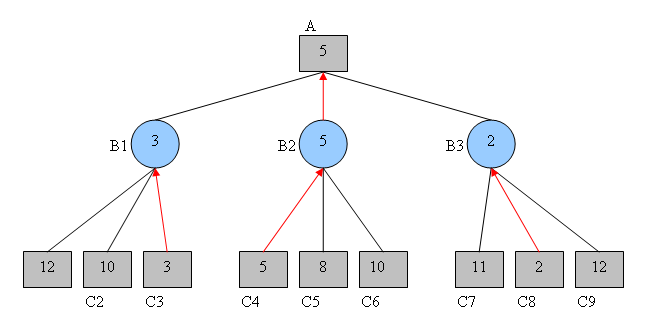
L’algorithme minimax consiste à alterner ces étapes de minimisations et de maximisations, afin de maximiser le gain que nous attendrions finalement en prenant une décision.
Il est important de noter que l’algorithme maximin ne retournera pas la séquence de coups qui mène au gain le plus élevé possible (qui dans l’exemple ci-dessus serait $C9$ avec un gain de 12), mais la séquence de jeu la moins pire, i.e., celle qui mène de manière réaliste à notre meilleur gain.
Pour conclure, notez qu’ici nous alternons les décisions entre les joueurs, ce qui implique qu’ils prennent leurs décisions à tour de rôle. Néanmoins, il existe des résultats équivalents pour les jeux simultanés tels que PyRat.
Pour aller encore plus loin
- Minimax Algorithm in Game Theory.
Quelques codes pour implémenter un algorithme minimax.