Activité pratique

Durée2h30

Consignes globales

L’objectif de cette activité est d’écrire des programmes pour guider votre rat à travers le labyrinthe grâce à des algorithmes de parcours. Nous allons tout d’abord nous placer dans un cas simple :

  • Un seul joueur.
  • Un seul morceau de fromage à attraper.
  • Pas de boue dans le labyrinthe.

Contenu de l’activité

1 — Parcours en profondeur (DFS)

1.1 — Préparation

Tout d’abord, nous allons créer un joueur et un script pour visualiser son comportement.

À faire

Avant de commencer, créez les fichiers nécessaires dans votre workspace PyRat en suivant les instructions ci-dessous.

Correction

Comme indiqué dans les instructions, vous devez créer une classe héritant de Player, nommée DFS, dans un fichier DFS.py dans le sous-dossier players de pyrat_workspace. Faites attention à ce que turn(...) renvoie bien une action, qui peut être Action.NOTHING.

Il serait aussi bien de mettre à jour les documentations pour que ça corresponde au parcours en profondeur et pas à un RandomX ou TemplatePlayer selon de quel fichier vous êtes partis.

Vous devez également créer un script visualize_DFS.py dans le sous-dossier games. Attention à bien fixer les arguments mud_percentage et nb_cheese du constructeur de la classe Game. Le fichier devrait ressembler à ça :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import pprint

# PyRat imports
from pyrat import Game
from players.DFS import DFS

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Instantiate a game with a few arguments
    game_config = {"mud_percentage": 0.0,
                   "maze_width": 13,
                   "maze_height": 10,
                   "nb_cheese": 1,
                   "random_seed": 42,
                   "trace_length": 1000}

    # Instantiate a game with specified arguments
    game = Game(**game_config)

    # Instantiate the player
    player = DFS()
    game.add_player(player)

    # Start the game
    stats = game.start()
    pprint.pprint(stats)

##########################################################################################
##########################################################################################

  • players/DFS.py – Inspirez vous de ce que vous avez fait en séance 1 pour créer un joueur DFS héritant de Player, et ayant :

    • Un constructeur __init__(...).
    • Une méthode preprocessing(...).
    • Une méthode turn(...).

    Dans un premier temps, ne vous préoccupez pas du comportement de votre joueur, créez juste le strict minimum pour pouvoir lancer une partie avec votre joueur DFS sans que ça crashe.

  • games/visualize_DFS.py – Créez un fichier qui lancera une partie avec un joueur DFS, dans un labyrinthe respectant les critères listés plus haut. Vous pouvez éventuellement définir une random_seed (pour toujours travailler avec le même labyrinthe) et une trace_length (pour suivre la trajectoire de votre joueur). Inspirez-vous des autres fichiers du sous-dossier games que vous avez rencontrés lors de la séance précédente.

1.2 — La méthode traversal(...)

1.2.1 — Implémentation

Comme vous avez pu l’étudier dans vos cours de programmation et d’algorithmique, la clé pour écrire un bon programme est de bien décomposer les tâches à effectuer en fonctions. Pour cela, au lieu d’effectuer directement le parcours dans une des méthodes du joueur, on vous demande d’écrire une méthode traversal(...) qui effectuera le parcours en profondeur, et renverra la table de routage correspondante.

À faire

Copiez-collez le code suivant dans votre fichier DFS.py, et complétez la méthode.

Correction

À terme, le programme devrait ressembler à ça :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# PyRat imports
from pyrat import Player, Maze, GameState, Action, Graph

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class DFS (Player):

    """
    *(This class inherits from* ``Player`` *).*

    This player performs a depth-first search (DFS) to explore the maze.
    Computation of the path is done in the ``preprocessing(...)`` method.
    The path is then followed in the ``turn(...)`` method.
    """
    
    ##################################################################################
    #                                   CONSTRUCTOR                                  #
    ##################################################################################

    def __init__ ( self,
                   *args:    object,
                   **kwargs: object
                 ) ->        None:

        """
        Initializes a new instance of the class.

        Args:
            args:   Arguments to pass to the parent constructor.
            kwargs: Keyword arguments to pass to the parent constructor.
        """

        # Inherit from parent class
        super().__init__(*args, **kwargs)

        # We create an attribute to store the actions to perform
        self.actions = None

    ##################################################################################
    #                                  PYRAT METHODS                                 #
    ##################################################################################

    def preprocessing ( self,
                        maze:       Maze,
                        game_state: GameState,
                      ) ->          None:
        
        """
        *(This method redefines the method of the parent class with the same name).*

        This method is called once at the beginning of the game.
        Here, we use a DFS algorithm to compute a path that reaches the piece of cheese from the initial position of the player.
        The actions corresponding to the path are stored in the ``actions`` attribute, and will be used in the ``turn(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        """

        # We perform a DFS traversal of the maze graph from the initial position of the player
        my_location = game_state.player_locations[self.get_name()]
        distances, routing_table = self.traversal(maze, my_location)

        # Find the series of locations/actions to go from the player location to the first piece of cheese
        path = self.find_route(routing_table, my_location, game_state.cheese[0])
        self.actions = maze.locations_to_actions(path)

    ##################################################################################

    def turn ( self,
               maze:       Maze,
               game_state: GameState,
             ) ->          Action:

        """
        *(This method redefines the method of the parent class with the same name).*

        It is called at each turn of the game.
        It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
        The action is chosen by following the path computed in the ``preprocessing(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        
        Returns:
            One of the possible actions.
        """

        # At each turn, we perform the next action in the list of actions
        return self.actions.pop(0)

    ##################################################################################
    #                                  OTHER METHODS                                 #
    ##################################################################################

    def traversal ( self,
                    graph:  Graph,
                    source: int
                  ) ->      tuple[dict[int, int], dict[int, int | None]]:

        """
        This method performs a DFS traversal of a graph.
        It returns the explored vertices with associated distances.
        It also returns the routing table, that is, the parent of each vertex in the traversal.
        
        Args:
            graph:  The graph to traverse.
            source: The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).

        Returns:
            A tuple containing:
            - The distances from the source to each explored vertex.
            - The routing table, that is, the parent of each vertex in the traversal (None for the source).
        """

        # Initialization
        distances = {}
        routing_table = {}

        # Initialize the list of vertices to visit
        vertices_to_visit = []
        vertices_to_visit.append((0, source, None))

        # Traversal
        while vertices_to_visit:

            # Get the next vertex to visit
            distance, vertex, parent = vertices_to_visit.pop()

            # Skip if already visited
            # This can happen if a vertex was added multiple times to the list by different neighbors
            if vertex in distances:
                continue

            # Update the distances and routing table
            distances[vertex] = distance
            routing_table[vertex] = parent

            # Add the neighbors to the list of vertices to visit
            for neighbor in graph.get_neighbors(vertex):
                distance_to_neighbor = distances[vertex] + graph.get_weight(vertex, neighbor)
                vertices_to_visit.append((distance_to_neighbor, neighbor, vertex))
        
        # Return the result
        return distances, routing_table

    ##################################################################################

    def find_route ( self,
                     routing_table: dict[int, int | None],
                     source:        int,
                     target:        int
                   ) ->             list[int]:

        """
        This method finds the route from a source vertex to a target vertex using a routing table.

        Args:
            routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
            source:        The source vertex.
            target:        The target vertex.

        Returns:
            The route from the source to the target as a list of vertices.
        """

        # Initialization
        route = [target]
        vertex = target

        # Find the route
        while vertex != source:
            vertex = routing_table[vertex]
            route.append(vertex)
        
        # Reverse the route
        route.reverse()
        return route

##########################################################################################
##########################################################################################
​
def traversal ( self,
                graph:  Graph,
                source: int
              ) ->      tuple[dict[int, int], dict[int, int | None]]:

    """
    This method performs a DFS traversal of a graph.
    It returns the explored vertices with associated distances.
    It also returns the routing table, that is, the parent of each vertex in the traversal.

    Args:
        graph:  The graph to traverse.
        source: The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).

    Returns:
        A tuple containing:
        - The distances from the source to each explored vertex.
        - The routing table, that is, the parent of each vertex in the traversal (None for the source).
    """

    # Your code here
1.2.2 — Tests

Avez-vous bien pensé à vérifier que votre méthode traversal(...) fonctionne ? On peut souvent faire des erreurs en écrivant du code, que ça soit un détail de raisonnement oublié, un cas un peu inhabituel pas géré, ou juste une erreur de syntaxe. Par défaut, une bonne position est de partir du principe que tout code non testé est faux.

Vous avez vu en séance 2 de programmation comment exécuter des tests unitaires, et verrez en séance 3 comment en concevoir. Pour le moment, nous allons vous fournir un fichier de tests pour vérifier votre implémentation de traversal(...). Dans les prochaines séances de PyRat, vous aurez à créer vos propres tests.

À faire

Téléchargez le fichier ci-dessous, et placez le dans un nouveau dossier tests que vous créerez dans votre dossier pyrat_workspace.

Correction

Juste créer le dossier et coller le fichier test_DFS.py dedans.

Ce fichier présuppose que vous avez bien suivi les instructions jusqu’à présent, c’est-à-dire que votre joueur s’appelle bien DFS dans un fichier DFS.py, que traversal(...) a bien le prototype de la méthode donnée plus haut, etc.

Si vous avez bien compris l’algorithme de parcours en profondeur, vous devriez constater qu’il existe de nombreuses solutions possibles, selon l’ordre dans lequel les sommets voisins sont explorés. Pour cette raison, nous ne pouvons pas créer directement un test qui vérifierait que, pour un graphe donné, on obtient une table de routage particulière fixée à l’avance. À la place, nous allons évaluer des propriétés de la solution produite par la méthode traversal(...) sur un certain nombre de labyrinthes générés aléatoirement :

  • Les sorties sont des types attendus.

  • Tous les sommets sont visités (présuppose que le graphe le permet).

  • La table de routage forme un arbre, dont la racine correspond au sommet de départ du parcours.

  • Les distances trouvées sont valides, c’est-à-dire strictement positives et croissantes, sauf pour le sommet de départ qui doit être égal à 0.

En exécutant ce fichier, vous devriez obtenir la sortie suivante dans le terminal :

test_traversal (__main__.DFS_Tests.test_traversal)
This method tests the ``traversal(...)`` method. ... ok

----------------------------------------------------------------------
Ran 1 test in 1.603s

OK
Information

Le script test_DFS.py que vous venez de télécharger utilise une bibliothèque Python appelée unittest. Avec cette bibliothèque, vous pouvez définir des méthodes qui correspondent à des tests pour les fonctions ou méthodes que vous souhaitez évaluer.

L’appel à unittest.main(verbosity=2) en bas du script permet d’exécuter automatiquement toutes les méthodes s’appelant test_XXX(...). Si besoin, vous pouvez définir d’autres méthodes annexes, par exemple pour créer un graphe aléatoire. Tant que ces méthodes ne s’appellent pas test_XXX(...), elles ne seront pas évaluées par unittest.

La bibliothèque unittest fournit quelques méthodes particulièrement utiles :

  • self.assertTrue(e) – Le test échoue si l’expression e entre parenthèses n’est pas évaluée à True.
  • self.assertFalse(e) – Le test échoue si l’expression e entre parenthèses n’est pas évaluée à False.
  • self.assertEquals(e1, e2) – Le test échoue si l’évaluation de l’expression e1 entre parenthèses ne correspond pas à celle de l’expression e2.
  • with self.assertRaises(t): e – Le test échoue si l’évaluation de l’expression e ne lève pas une exception de type t.

En réalité, il existe d’autres méthodes permettant de tester l’égalité, l’appartenance à une liste, etc. Vous pouvez trouver la liste complète dans la documentation officielle.

En utilisant ces méthodes, vous pouvez définir un ensemble de tests qui cherchent à pousser votre code dans ses retranchements. Si tous les tests passent avec succès, vous pouvez alors avoir une bonne confiance dans le bon fonctionnement de votre code.

1.3 — Utiliser la table de routage

1.3.1 — Implémentation

Maintenant que vous avez un algorithme de parcours qui marche (et testé !), écrivons une méthode qui exploite la table de routage pour renvoyer la série de cases à suivre pour atteindre une case donnée.

À faire

Copiez-collez le code suivant dans votre fichier DFS.py en tant que méthode de la classe DFS. Puis, complétez la méthode pour renvoyer une liste de sommets du graphe telle que le premier élément est la source et le dernier la cible.

Correction

Voir le contenu de DFS.py dans une des boîtes de corrections plus haut.

​
def find_route ( self,
                 routing_table: dict[int, int | None],
                 source:        int,
                 target:        int
               ) ->             list[int]:

    """
    This method finds the route from a source vertex to a target vertex using a routing table.

    Args:
        routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
        source:        The source vertex.
        target:        The target vertex.

    Returns:
        The route from the source to the target as a list of vertices.
    """

    # Your code here
1.3.2 — Tests

Maintenant que nous avons écrit une nouvelle méthode, ajoutons quelques tests. Notez ici que, pour une table de routage donnée, avec des sommets source et cible fixés, il n’existe qu’une seule solution possible. Nous pouvons donc appeler la méthode sur des scénarios fixes, identifiés au préalable.

À faire

Copiez le code suivant dans votre fichier test_DFS.py, en tant que nouvelle méthode de votre classe DFS_Tests.

Correction

À terme, le fichier devrait ressembler à ça :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import random
import unittest

# PyRat imports
from pyrat import RandomMaze, RandomMazeAlgorithm, BigHolesRandomMaze, HolesOnSideRandomMaze, UniformHolesRandomMaze
from players.DFS import DFS

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class DFS_Tests (unittest.TestCase):

    """
    *(This class inherits from* ``unittest.TestCase`` *).*

    This class tests the methods of the DFS class.
    For each method, we test it with a few different configurations.
    """

    ##################################################################################
    #                                 INITIALIZATION                                 #
    ##################################################################################

    def setUp (self) -> None:

        """
        This method is called before each test method.
        It allows to factorize attributes that are common to all test methods.
        It is basically acting as a constructor, but it is called before each test method, not only once when the class is instantiated.
        """

        # Nothing to do here
        pass

    ##################################################################################
    #                                     CLEANUP                                    #
    ##################################################################################

    def tearDown (self) -> None:

        """
        This method is called after each test method.
        It allows to clean up any resources that were allocated in the `setUp(...)` method.
        """

        # Nothing to do here
        pass

    ##################################################################################
    #                                AUXILIARY METHODS                               #
    ##################################################################################
    
    def create_random_maze ( self,
                             maze_type:      RandomMazeAlgorithm,
                             maze_arguments: dict[str, object] = {}
                           ) ->              RandomMaze:

        """
        Create a random maze using the specified algorithm

        Args:
            maze_type:      The type of random maze to create.
            maze_arguments: Additional arguments to pass to the maze constructor.

        Returns:
            A random maze of the specified type.
        """

        # We create a maze
        if maze_type == RandomMazeAlgorithm.HOLES_ON_SIDE:
            maze = HolesOnSideRandomMaze(**maze_arguments)
        elif maze_type == RandomMazeAlgorithm.UNIFORM_HOLES:
            maze = UniformHolesRandomMaze(**maze_arguments)
        elif maze_type == RandomMazeAlgorithm.BIG_HOLES:
            maze = BigHolesRandomMaze(**maze_arguments)
        return maze

    ##################################################################################
    #                                      TESTS                                     #
    ##################################################################################

    def test_traversal (self) -> None:

        """
        This method tests the ``traversal(...)`` method.

        We are going to check the following:
        - Outputs are of the expected types.
        - All vertices are visited.
        - The routing table is a tree, with root corresponding to the start of the traversal.
        - The found distances are correct, i.e., strictly positive and increasing, except for the start vertex which should be 0.

        Note that we cannot test that the output is unique, as there are multiple valid outputs, depending on how vertices are explored.
        We will test the method on several random graphs to make sure it is working properly.
        Random graphs will be generated using the PyRat class used to create mazes in games.
        There are several such classes, but we will use the BigHolesRandomMaze class.
        """

        # Constants
        NB_GRAPHS = 10
        WIDTHS = [2, 30]
        HEIGHTS = [2, 30]
        CELL_PERCENTAGES = [20.0, 100.0]
        WALL_PERCENTAGES = [20.0, 100.0]
        MUD_PERCENTAGE = 0.0

        # Test on several graphs
        for i in range(NB_GRAPHS):
            
            # Instantiate the player
            player = DFS()

            # Generate a random maze
            # We use a fixed random seed for reproducibility of tests
            rng = random.Random(i)
            config = {"width": rng.randint(WIDTHS[0], WIDTHS[1]),
                      "height": rng.randint(HEIGHTS[0], HEIGHTS[1]),
                      "cell_percentage": rng.uniform(CELL_PERCENTAGES[0], CELL_PERCENTAGES[1]),
                      "wall_percentage": rng.uniform(WALL_PERCENTAGES[0], WALL_PERCENTAGES[1]),
                      "mud_percentage": MUD_PERCENTAGE,
                      "random_seed": i}
            maze = self.create_random_maze(RandomMazeAlgorithm.BIG_HOLES, config)

            # Choose a random starting vertex
            start_vertex = rng.choice(maze.get_vertices())

            # Perform the traversal
            distances, routing_table = player.traversal(maze, start_vertex)

            # Check the output type for distances
            # It should be a dictionary with integer keys and integer values
            self.assertTrue(isinstance(distances, dict))
            self.assertTrue(all(isinstance(k, int) for k in distances.keys()))
            self.assertTrue(all(isinstance(v, int) for v in distances.values()))
            
            # Check the output type for the routing table
            # It should be a dictionary with integer keys and integer or None values
            self.assertTrue(isinstance(routing_table, dict))
            self.assertTrue(all(isinstance(k, int) for k in routing_table.keys()))
            self.assertTrue(all(isinstance(v, (type(None), int)) for v in routing_table.values()))

            # All vertices should be visited
            # Equivalently, the distances should have the same keys as the maze vertices
            self.assertEqual(sorted(set(distances.keys())), sorted(maze.get_vertices()))

            # Check that the start vertex is the only tree root
            self.assertEqual(routing_table[start_vertex], None)
            self.assertTrue(all(routing_table[v] is not None for v in routing_table.keys() if v != start_vertex))
            self.assertEqual(distances[start_vertex], 0)
            self.assertTrue(all(distances[v] > 0 for v in distances.keys() if v != start_vertex))
            
            # We check that the routing table is a tree
            # Also we check that associated distances are decreasing as we go to the root
            for vertex in routing_table:

                # We check that the parent is closer to the root
                if routing_table[vertex] is not None:
                    self.assertTrue(distances[routing_table[vertex]] < distances[vertex])
                
                # We ckeck that we can reach the root from any vertex
                path = [vertex]
                while routing_table[path[-1]] is not None:
                    self.assertTrue(routing_table[path[-1]] not in path)
                    path.append(routing_table[path[-1]])

    ##################################################################################

    def test_find_route (self) -> None:
        
        """
        This method tests the ``find_route(...)`` method.
        Here, we want to make sure that the output corresponds indeed to a route from the start to the end.

        We are going to check the following:
        - Outputs are of the expected types.
        - The route is a valid path from the start to the end.

        The method will be tested on some controlled examples, where we can easily check the validity of the output.
        """

        # Constants
        INPUTS = [{"routing_table": {0: None, 1: 0, 2: 1, 3: 2, 4: 3},
                   "start": 0,
                   "end": 4},
                  {"routing_table": {0: 2, 1: None, 2: 1, 3: 0, 4: 0, 5: 4, 6: 1},
                   "start": 1,
                   "end": 6}]

        # Test on several controlled examples
        for i in range(len(INPUTS)):
            
            # Instantiate the player
            player = DFS()

            # Get the input data
            routing_table = INPUTS[i]["routing_table"]
            start = INPUTS[i]["start"]
            end = INPUTS[i]["end"]

            # Find the route
            route = player.find_route(routing_table, start, end)

            # Check the output type
            # It should be a list of integers
            self.assertTrue(isinstance(route, list))
            self.assertTrue(all(isinstance(v, int) for v in route))

            # Check that the route is a valid path from the start to the end
            self.assertEqual(route[0], start)
            self.assertEqual(route[-1], end)
            self.assertTrue(all(routing_table[route[j + 1]] == route[j] for j in range(len(route) - 1)))

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Run all tests
    unittest.main(verbosity=2)

##########################################################################################
##########################################################################################
​
def test_find_route (self) -> None:

    """
    This method tests the ``find_route(...)`` method.
    Here, we want to make sure that the output corresponds indeed to a route from the start to the end.

    We are going to check the following:
    - Outputs are of the expected types.
    - The route is a valid path from the start to the end.

    The method will be tested on some controlled examples, where we can easily check the validity of the output.
    """

    # Constants
    INPUTS = [{"routing_table": {0: None, 1: 0, 2: 1, 3: 2, 4: 3},
               "start": 0,
               "end": 4},
              {"routing_table": {0: 2, 1: None, 2: 1, 3: 0, 4: 0, 5: 4, 6: 1},
               "start": 1,
               "end": 6}]

    # Test on several controlled examples
    for i in range(len(INPUTS)):

        # Instantiate the player
        player = DFS()

        # Get the input data
        routing_table = INPUTS[i]["routing_table"]
        start = INPUTS[i]["start"]
        end = INPUTS[i]["end"]

        # Find the route
        route = player.find_route(routing_table, start, end)

        # Check the output type
        # It should be a list of integers
        self.assertTrue(isinstance(route, list))
        self.assertTrue(all(isinstance(v, int) for v in route))

        # Check that the route is a valid path from the start to the end
        self.assertEqual(route[0], start)
        self.assertEqual(route[-1], end)
        self.assertTrue(all(routing_table[route[j + 1]] == route[j] for j in range(len(route) - 1)))

Ici, nous définissons deux tables de routage fixes et les utilisons comme entrées pour tester la méthode find_route(...). Nous aurions pu en définir beaucoup d’autres, et également utiliser des tables de routage valides générées aléatoirement à partir de la fonction traversal(...) que nous avons précédemment développée et validée.

Dans ces tests, nous effectuons les vérifications suivantes :

  • Le type de sortie est valide.

  • Les parents dans la table de routage apparaissent bien comme prédécesseurs dans le chemin obtenu.

  • Le chemin va bien du point de départ à la destination.

En relançant votre script de tests, vous devriez obtenir la sortie suivante :

This method tests the ``find_route(...)`` method. ... ok
test_traversal (__main__.DFS_Tests.test_traversal)
This method tests the ``traversal(...)`` method. ... ok

----------------------------------------------------------------------
Ran 2 tests in 1.649s

OK

1.4 — Assembler tout ça

1.4.1 — Implémentation

Maintenant, il ne reste plus qu’à assembler les morceaux !

À faire

Apportez les modifications suivantes à votre fichier DFS.py.

Correction

Voir le contenu de DFS.py dans une des boîtes de corrections plus haut.

  • __init__(...) – Mettez à jour votre constructeur afin de déclarer un attribut self.actions = None. Vous pourriez directement l’initialiser avec une liste vide [], mais il est préférable de l’initialiser dans preprocessing(...) pour permettre de faire un reset(...) de la partie sans avoir des valeurs restantes de la partie précédente dans les attributs du joueur.

  • preprocessing(...) – Pendant la phase de prétraitement, utilisez les méthodes introduites précédemment (traversal(...) et find_route(...)) pour calculer les actions à effectuer depuis votre position initiale (my_location = game_state.player_locations[self.get_name()]) jusqu’à la position du seul morceau de fromage (cheese_location = game_state.cheese[0]). Ensuite, stockez ces actions dans l’attribut self.actions.

    Information

    Pour obtenir des actions à partir d’un chemin, la classe Maze fournit une méthode locations_to_actions(...).

  • turn(...) – À chaque tour, vous devez retourner une action provenant de self.actions. Il suffit d’extraire la prochaine action à effectuer depuis cet attribut et de la renvoyer.

1.4.2 — Tests

À présent, utilisez votre script visualize_DFS.py pour observer votre joueur.

À faire

Son comportement est-il bon ? Pensez à l’étudier sur quelques labyrinthes distincts.

Correction

Le rat n’est pas censé revenir sur ses pas. Il a déroulé un algorithme en mémoire qui a déterminé un chemin (suite distincte de sommets). C’est un bon indicateur que ça se passe bien.

Pensez à tester sur plusieurs labyrinthes.

Vous devriez obtenir un rat qui se comporte comme suit :

2 — Parcours en largeur (BFS)

Comme vous avez pu le voir dans la vidéo précédente, le DFS trouve un chemin qui n’est pas exactement le plus court. Nous allons maintenant utiliser un autre algorithme, appelé parcours en largeur (Breadth-First Search, BFS). Cet algorithme a la propriété de renvoyer le chemin le plus court dans un graphe non pondéré.

À faire

Suivez les mêmes étapes que précédemment (rappelées ci-dessous) pour créer un joueur qui suit un chemin trouvé par l’algorithme BFS pour attraper le morceau de fromage.

Correction

Les fichiers à produire :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# PyRat imports
from pyrat import Player, Maze, GameState, Action, Graph

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class BFS (Player):

    """
    *(This class inherits from* ``Player`` *).*

    This player performs a breadth-first search (BFS) to explore the maze.
    Computation of the path is done in the ``preprocessing(...)`` method.
    The path is then followed in the ``turn(...)`` method.
    """

    ##################################################################################
    #                                   CONSTRUCTOR                                  #
    ##################################################################################

    def __init__ ( self,
                   *args:    object,
                   **kwargs: object
                 ) ->        None:

        """
        Initializes a new instance of the class.

        Args:
            args:   Arguments to pass to the parent constructor.
            kwargs: Keyword arguments to pass to the parent constructor.
        """

        # Inherit from parent class
        super().__init__(*args, **kwargs)

        # We create an attribute to store the actions to perform
        self.actions = None

    ##################################################################################
    #                                  PYRAT METHODS                                 #
    ##################################################################################

    def preprocessing ( self,
                        maze:       Maze,
                        game_state: GameState,
                      ) ->          None:
        
        """
        *(This method redefines the method of the parent class with the same name).*

        This method is called once at the beginning of the game.
        Here, we use a BFS algorithm to compute a shortest path that reaches the piece of cheese from the initial position of the player.
        The actions corresponding to the path are stored in the ``actions`` attribute, and will be used in the ``turn(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        """

        # We perform a BFS traversal of the maze graph from the initial position of the player
        my_location = game_state.player_locations[self.get_name()]
        distances, routing_table = self.traversal(maze, my_location)

        # Find the series of locations/actions to go from the player location to the first piece of cheese
        path = self.find_route(routing_table, my_location, game_state.cheese[0])
        self.actions = maze.locations_to_actions(path)

    ##################################################################################

    def turn ( self,
               maze:       Maze,
               game_state: GameState,
             ) ->          Action:

        """
        *(This method redefines the method of the parent class with the same name).*

        It is called at each turn of the game.
        It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
        The action is chosen by following the path computed in the ``preprocessing(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        
        Returns:
            One of the possible actions.
        """

        # At each turn, we perform the next action in the list of actions
        return self.actions.pop(0)

    ##################################################################################
    #                                  OTHER METHODS                                 #
    ##################################################################################

    def traversal ( self,
                    graph:  Graph,
                    source: int
                  ) ->      tuple[dict[int, int], dict[int, int | None]]:

        """
        This method performs a BFS traversal of a graph.
        It returns the explored vertices with associated distances.
        It also returns the routing table, that is, the parent of each vertex in the traversal.
        
        Args:
            graph:  The graph to traverse.
            source: The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).

        Returns:
            A tuple containing:
            - The distances from the source to each explored vertex.
            - The routing table, that is, the parent of each vertex in the traversal (None for the source).
        """

        # Initialization
        distances = {}
        routing_table = {}

        # Initialize the list of vertices to visit
        vertices_to_visit = []
        vertices_to_visit.append((0, source, None))

        # Traversal
        while vertices_to_visit:

            # Get the next vertex to visit
            distance, vertex, parent = vertices_to_visit.pop(0)

            # Skip if already visited
            # This can happen if a vertex was added multiple times to the list by different neighbors
            if vertex in distances:
                continue

            # Update the distances and routing table
            distances[vertex] = distance
            routing_table[vertex] = parent

            # Add the neighbors to the list of vertices to visit
            for neighbor in graph.get_neighbors(vertex):
                distance_to_neighbor = distances[vertex] + graph.get_weight(vertex, neighbor)
                vertices_to_visit.append((distance_to_neighbor, neighbor, vertex))
        
        # Return the result
        return distances, routing_table

    ##################################################################################

    def find_route ( self,
                     routing_table: dict[int, int | None],
                     source:        int,
                     target:        int
                   ) ->             list[int]:

        """
        This method finds the route from a source vertex to a target vertex using a routing table.

        Args:
            routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
            source:        The source vertex.
            target:        The target vertex.

        Returns:
            The route from the source to the target as a list of vertices.
        """

        # Initialization
        route = [target]
        vertex = target

        # Find the route
        while vertex != source:
            vertex = routing_table[vertex]
            route.append(vertex)
        
        # Reverse the route
        route.reverse()
        return route

##########################################################################################
##########################################################################################
​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import pprint

# PyRat imports
from pyrat import Game
from players.BFS import BFS

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Instantiate a game with a few arguments
    game_config = {"mud_percentage": 0.0,
                   "maze_width": 13,
                   "maze_height": 10,
                   "nb_cheese": 1,
                   "random_seed": 42,
                   "trace_length": 1000}

    # Instantiate a game with specified arguments
    game = Game(**game_config)

    # Instantiate the player
    player = BFS()
    game.add_player(player)

    # Start the game
    stats = game.start()
    pprint.pprint(stats)

##########################################################################################
##########################################################################################
​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import random
import unittest

# PyRat imports
from pyrat import MazeFromDict, RandomMaze, RandomMazeAlgorithm, BigHolesRandomMaze, HolesOnSideRandomMaze, UniformHolesRandomMaze
from players.BFS import BFS

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class BFS_Tests (unittest.TestCase):

    """
    *(This class inherits from* ``unittest.TestCase`` *).*

    This class tests the methods of the BFS class.
    For each method, we test it with a few different configurations.
    """

    ##################################################################################
    #                                 INITIALIZATION                                 #
    ##################################################################################

    def setUp (self) -> None:

        """
        This method is called before each test method.
        It allows to factorize attributes that are common to all test methods.
        It is basically acting as a constructor, but it is called before each test method, not only once when the class is instantiated.
        """

        # Nothing to do here
        pass

    ##################################################################################
    #                                     CLEANUP                                    #
    ##################################################################################

    def tearDown (self) -> None:

        """
        This method is called after each test method.
        It allows to clean up any resources that were allocated in the `setUp(...)` method.
        """

        # Nothing to do here
        pass

    ##################################################################################
    #                                AUXILIARY METHODS                               #
    ##################################################################################
    
    def create_random_maze ( self,
                             maze_type:      RandomMazeAlgorithm,
                             maze_arguments: dict[str, object] = {}
                           ) ->              RandomMaze:

        """
        Create a random maze using the specified algorithm

        Args:
            maze_type:      The type of random maze to create.
            maze_arguments: Additional arguments to pass to the maze constructor.

        Returns:
            A random maze of the specified type.
        """

        # We create a maze
        if maze_type == RandomMazeAlgorithm.HOLES_ON_SIDE:
            maze = HolesOnSideRandomMaze(**maze_arguments)
        elif maze_type == RandomMazeAlgorithm.UNIFORM_HOLES:
            maze = UniformHolesRandomMaze(**maze_arguments)
        elif maze_type == RandomMazeAlgorithm.BIG_HOLES:
            maze = BigHolesRandomMaze(**maze_arguments)
        return maze

    ##################################################################################
    #                                      TESTS                                     #
    ##################################################################################

    def test_traversal_random (self) -> None:

        """
        This method tests the ``traversal(...)`` method.

        We are going to check the following:
        - Outputs are of the expected types.
        - All vertices are visited.
        - The routing table is a tree, with root corresponding to the start of the traversal.
        - The found distances are correct, i.e., strictly positive and increasing, except for the start vertex which should be 0.

        Note that we cannot test that the output is unique, as there are multiple valid outputs, depending on how vertices are explored.
        We will test the method on several random graphs to make sure it is working properly.
        Random graphs will be generated using the PyRat class used to create mazes in games.
        There are several such classes, but we will use the BigHolesRandomMaze class.
        """

        # Constants
        NB_GRAPHS = 10
        WIDTHS = [2, 30]
        HEIGHTS = [2, 30]
        CELL_PERCENTAGES = [20.0, 100.0]
        WALL_PERCENTAGES = [20.0, 100.0]
        MUD_PERCENTAGE = 0.0

        # Test on several graphs
        for i in range(NB_GRAPHS):
            
            # Instantiate the player
            player = BFS()

            # Generate a random maze
            # We use a fixed random seed for reproducibility of tests
            rng = random.Random(i)
            config = {"width": rng.randint(WIDTHS[0], WIDTHS[1]),
                      "height": rng.randint(HEIGHTS[0], HEIGHTS[1]),
                      "cell_percentage": rng.uniform(CELL_PERCENTAGES[0], CELL_PERCENTAGES[1]),
                      "wall_percentage": rng.uniform(WALL_PERCENTAGES[0], WALL_PERCENTAGES[1]),
                      "mud_percentage": MUD_PERCENTAGE,
                      "random_seed": i}
            maze = self.create_random_maze(RandomMazeAlgorithm.BIG_HOLES, config)

            # Choose a random starting vertex
            start_vertex = rng.choice(maze.get_vertices())

            # Perform the traversal
            distances, routing_table = player.traversal(maze, start_vertex)

            # Check the output type for distances
            # It should be a dictionary with integer keys and integer values
            self.assertTrue(isinstance(distances, dict))
            self.assertTrue(all(isinstance(k, int) for k in distances.keys()))
            self.assertTrue(all(isinstance(v, int) for v in distances.values()))
            
            # Check the output type for the routing table
            # It should be a dictionary with integer keys and integer or None values
            self.assertTrue(isinstance(routing_table, dict))
            self.assertTrue(all(isinstance(k, int) for k in routing_table.keys()))
            self.assertTrue(all(isinstance(v, (type(None), int)) for v in routing_table.values()))

            # All vertices should be visited
            # Equivalently, the distances should have the same keys as the maze vertices
            self.assertEqual(sorted(set(distances.keys())), sorted(maze.get_vertices()))

            # Check that the start vertex is the only tree root
            self.assertEqual(routing_table[start_vertex], None)
            self.assertTrue(all(routing_table[v] is not None for v in routing_table.keys() if v != start_vertex))
            self.assertEqual(distances[start_vertex], 0)
            self.assertTrue(all(distances[v] > 0 for v in distances.keys() if v != start_vertex))
            
            # We check that the routing table is a tree
            # Also we check that associated distances are decreasing as we go to the root
            for vertex in routing_table:

                # We check that the parent is closer to the root
                if routing_table[vertex] is not None:
                    self.assertTrue(distances[routing_table[vertex]] < distances[vertex])
                
                # We ckeck that we can reach the root from any vertex
                path = [vertex]
                while routing_table[path[-1]] is not None:
                    self.assertTrue(routing_table[path[-1]] not in path)
                    path.append(routing_table[path[-1]])

    ##################################################################################

    def test_traversal_fixed (self) -> None:
         
        """
        This method complements the previous tests by testing the `traversal(...)` method on some controlled examples.
        To do so, we will use some mazes for which there is a unique routing table.
        We do not test the output types again, as it has already been done in the previous test function.
        """

        # Constants
        TESTS = [{"inputs": {"maze": MazeFromDict({4: {5: 1}, 5: {4: 1, 6: 1}, 6: {5: 1, 16: 1}, 7: {17: 1}, 9: {19: 1}, 10: {20: 1}, 11: {12: 1}, 12: {11: 1, 22: 1}, 16: {6: 1, 17: 1, 26: 1}, 17: {7: 1, 16: 1}, 19: {9: 1, 29: 1}, 20: {10: 1, 30: 1}, 21: {22: 1}, 22: {12: 1, 21: 1, 23: 1, 32: 1}, 23: {22: 1}, 24: {34: 1}, 26: {16: 1, 27: 1, 36: 1}, 27: {26: 1, 28: 1, 37: 1}, 28: {27: 1, 29: 1}, 29: {19: 1, 28: 1}, 30: {20: 1, 40: 1}, 31: {32: 1, 41: 1}, 32: {22: 1, 31: 1, 33: 1}, 33: {32: 1, 34: 1}, 34: {24: 1, 33: 1, 44: 1}, 36: {26: 1, 46: 1}, 37: {27: 1}, 40: {30: 1, 41: 1}, 41: {31: 1, 40: 1, 51: 1}, 43: {44: 1}, 44: {34: 1, 43: 1, 45: 1}, 45: {44: 1, 46: 1}, 46: {36: 1, 45: 1, 47: 1}, 47: {46: 1, 48: 1}, 48: {47: 1}, 50: {51: 1}, 51: {41: 1, 50: 1, 52: 1, 61: 1}, 52: {51: 1, 53: 1}, 53: {52: 1, 54: 1}, 54: {53: 1, 55: 1}, 55: {54: 1, 56: 1, 65: 1}, 56: {55: 1, 57: 1}, 57: {56: 1, 58: 1, 67: 1}, 58: {57: 1, 68: 1}, 60: {61: 1}, 61: {51: 1, 60: 1, 71: 1}, 65: {55: 1}, 66: {67: 1}, 67: {57: 1, 66: 1, 77: 1}, 68: {58: 1, 78: 1}, 69: {79: 1}, 70: {71: 1, 80: 1}, 71: {61: 1, 70: 1, 72: 1}, 72: {71: 1, 73: 1}, 73: {72: 1, 74: 1}, 74: {73: 1, 75: 1}, 75: {74: 1}, 77: {67: 1, 87: 1}, 78: {68: 1, 79: 1}, 79: {69: 1, 78: 1, 89: 1}, 80: {70: 1, 90: 1}, 81: {91: 1}, 82: {83: 1, 92: 1}, 83: {82: 1, 84: 1}, 84: {83: 1, 94: 1}, 85: {95: 1}, 86: {96: 1}, 87: {77: 1, 88: 1, 97: 1}, 88: {87: 1}, 89: {79: 1, 99: 1}, 90: {80: 1, 91: 1}, 91: {81: 1, 90: 1, 92: 1}, 92: {82: 1, 91: 1, 93: 1}, 93: {92: 1}, 94: {84: 1, 95: 1}, 95: {85: 1, 94: 1, 96: 1}, 96: {86: 1, 95: 1}, 97: {87: 1, 98: 1}, 98: {97: 1}, 99: {89: 1}}),
                             "start": 55},
                  "outputs": {"routing_table": {55: None, 54: 55, 56: 55, 65: 55, 53: 54, 57: 56, 52: 53, 58: 57, 67: 57, 51: 52, 68: 58, 66: 67, 77: 67, 41: 51, 50: 51, 61: 51, 78: 68, 87: 77, 31: 41, 40: 41, 60: 61, 71: 61, 79: 78, 88: 87, 97: 87, 32: 31, 30: 40, 70: 71, 72: 71, 69: 79, 89: 79, 98: 97, 22: 32, 33: 32, 20: 30, 80: 70, 73: 72, 99: 89, 12: 22, 21: 22, 23: 22, 34: 33, 10: 20, 90: 80, 74: 73, 11: 12, 24: 34, 44: 34, 91: 90, 75: 74, 43: 44, 45: 44, 81: 91, 92: 91, 46: 45, 82: 92, 93: 92, 36: 46, 47: 46, 83: 82, 26: 36, 48: 47, 84: 83, 16: 26, 27: 26, 94: 84, 6: 16, 17: 16, 28: 27, 37: 27, 95: 94, 5: 6, 7: 17, 29: 28, 85: 95, 96: 95, 4: 5, 19: 29, 86: 96, 9: 19},
                              "distances": {55: 0, 54: 1, 56: 1, 65: 1, 53: 2, 57: 2, 52: 3, 58: 3, 67: 3, 51: 4, 68: 4, 66: 4, 77: 4, 41: 5, 50: 5, 61: 5, 78: 5, 87: 5, 31: 6, 40: 6, 60: 6, 71: 6, 79: 6, 88: 6, 97: 6, 32: 7, 30: 7, 70: 7, 72: 7, 69: 7, 89: 7, 98: 7, 22: 8, 33: 8, 20: 8, 80: 8, 73: 8, 99: 8, 12: 9, 21: 9, 23: 9, 34: 9, 10: 9, 90: 9, 74: 9, 11: 10, 24: 10, 44: 10, 91: 10, 75: 10, 43: 11, 45: 11, 81: 11, 92: 11, 46: 12, 82: 12, 93: 12, 36: 13, 47: 13, 83: 13, 26: 14, 48: 14, 84: 14, 16: 15, 27: 15, 94: 15, 6: 16, 17: 16, 28: 16, 37: 16, 95: 16, 5: 17, 7: 17, 29: 17, 85: 17, 96: 17, 4: 18, 19: 18, 86: 18, 9: 19}}},
                 {"inputs": {"maze": MazeFromDict({0: {1: 1}, 1: {0: 1, 11: 1}, 4: {5: 1}, 5: {4: 1, 6: 1}, 6: {5: 1, 7: 1, 16: 1}, 7: {6: 1}, 8: {9: 1, 18: 1}, 9: {8: 1}, 10: {11: 1}, 11: {1: 1, 10: 1, 21: 1}, 14: {24: 1}, 15: {16: 1}, 16: {6: 1, 15: 1, 17: 1, 26: 1}, 17: {16: 1, 18: 1, 27: 1}, 18: {8: 1, 17: 1, 19: 1}, 19: {18: 1}, 20: {21: 1}, 21: {11: 1, 20: 1, 31: 1}, 23: {24: 1}, 24: {14: 1, 23: 1, 25: 1}, 25: {24: 1, 26: 1}, 26: {16: 1, 25: 1, 36: 1}, 27: {17: 1, 28: 1}, 28: {27: 1, 29: 1}, 29: {28: 1, 39: 1}, 30: {31: 1}, 31: {21: 1, 30: 1, 41: 1}, 32: {42: 1}, 36: {26: 1, 37: 1}, 37: {36: 1, 38: 1, 47: 1}, 38: {37: 1, 48: 1}, 39: {29: 1}, 40: {41: 1}, 41: {31: 1, 40: 1, 42: 1}, 42: {32: 1, 41: 1, 52: 1}, 47: {37: 1, 57: 1}, 48: {38: 1, 49: 1, 58: 1}, 49: {48: 1, 59: 1}, 50: {51: 1}, 51: {50: 1, 61: 1}, 52: {42: 1, 62: 1}, 56: {57: 1}, 57: {47: 1, 56: 1}, 58: {48: 1, 68: 1}, 59: {49: 1}, 60: {70: 1}, 61: {51: 1, 62: 1}, 62: {52: 1, 61: 1, 63: 1}, 63: {62: 1, 73: 1}, 70: {60: 1, 71: 1}, 71: {70: 1, 72: 1}, 72: {71: 1, 73: 1, 82: 1}, 73: {63: 1, 72: 1, 74: 1, 83: 1}, 74: {73: 1, 75: 1, 84: 1}, 75: {74: 1, 85: 1}, 76: {77: 1, 86: 1}, 77: {76: 1, 78: 1, 87: 1}, 78: {77: 1, 79: 1, 88: 1, 68: 1}, 79: {78: 1, 89: 1}, 80: {81: 1}, 81: {80: 1, 82: 1}, 82: {72: 1, 81: 1, 92: 1}, 83: {73: 1}, 84: {74: 1}, 85: {75: 1, 86: 1, 95: 1}, 86: {76: 1, 85: 1}, 87: {77: 1}, 88: {78: 1, 98: 1}, 89: {79: 1}, 90: {91: 1}, 91: {90: 1, 92: 1}, 92: {82: 1, 91: 1}, 93: {94: 1}, 94: {93: 1, 95: 1}, 95: {85: 1, 94: 1}, 96: {97: 1}, 97: {96: 1, 98: 1}, 98: {88: 1, 97: 1, 99: 1}, 99: {98: 1}, 68: {58: 1, 78: 1}}),
                             "start": 56},
                  "outputs": {"routing_table": {56: None, 57: 56, 47: 57, 37: 47, 36: 37, 38: 37, 26: 36, 48: 38, 16: 26, 25: 26, 49: 48, 58: 48, 6: 16, 15: 16, 17: 16, 24: 25, 59: 49, 68: 58, 5: 6, 7: 6, 18: 17, 27: 17, 14: 24, 23: 24, 78: 68, 4: 5, 8: 18, 19: 18, 28: 27, 77: 78, 79: 78, 88: 78, 9: 8, 29: 28, 76: 77, 87: 77, 89: 79, 98: 88, 39: 29, 86: 76, 97: 98, 99: 98, 85: 86, 96: 97, 75: 85, 95: 85, 74: 75, 94: 95, 73: 74, 84: 74, 93: 94, 63: 73, 72: 73, 83: 73, 62: 63, 71: 72, 82: 72, 52: 62, 61: 62, 70: 71, 81: 82, 92: 82, 42: 52, 51: 61, 60: 70, 80: 81, 91: 92, 32: 42, 41: 42, 50: 51, 90: 91, 31: 41, 40: 41, 21: 31, 30: 31, 11: 21, 20: 21, 1: 11, 10: 11, 0: 1},
                              "distances": {56: 0, 57: 1, 47: 2, 37: 3, 36: 4, 38: 4, 26: 5, 48: 5, 16: 6, 25: 6, 49: 6, 58: 6, 6: 7, 15: 7, 17: 7, 24: 7, 59: 7, 68: 7, 5: 8, 7: 8, 18: 8, 27: 8, 14: 8, 23: 8, 78: 8, 4: 9, 8: 9, 19: 9, 28: 9, 77: 9, 79: 9, 88: 9, 9: 10, 29: 10, 76: 10, 87: 10, 89: 10, 98: 10, 39: 11, 86: 11, 97: 11, 99: 11, 85: 12, 96: 12, 75: 13, 95: 13, 74: 14, 94: 14, 73: 15, 84: 15, 93: 15, 63: 16, 72: 16, 83: 16, 62: 17, 71: 17, 82: 17, 52: 18, 61: 18, 70: 18, 81: 18, 92: 18, 42: 19, 51: 19, 60: 19, 80: 19, 91: 19, 32: 20, 41: 20, 50: 20, 90: 20, 31: 21, 40: 21, 21: 22, 30: 22, 11: 23, 20: 23, 1: 24, 10: 24, 0: 25}}}]
                
        # Test on several controlled examples
        for i in range(len(TESTS)):
            
            # Instantiate the player
            player = BFS()

            # Get the input and output data
            maze = TESTS[i]["inputs"]["maze"]
            start = TESTS[i]["inputs"]["start"]
            target_routing_table = TESTS[i]["outputs"]["routing_table"]
            target_distances = TESTS[i]["outputs"]["distances"]

            # Perform the traversal
            distances, routing_table = player.traversal(maze, start)

            # Check that outputs match the expected ones
            self.assertEqual(sorted(routing_table), sorted(target_routing_table))
            self.assertEqual(sorted(distances), sorted(target_distances))
            
    ##################################################################################

    def test_find_route (self) -> None:
        
        """
        This method tests the ``find_route(...)`` method.
        Here, we want to make sure that the output corresponds indeed to a route from the start to the end.

        We are going to check the following:
        - Outputs are of the expected types.
        - The route is a valid path from the start to the end.

        The method will be tested on some controlled examples, where we can easily check the validity of the output.
        """

        # Constants
        INPUTS = [{"routing_table": {0: None, 1: 0, 2: 1, 3: 2, 4: 3},
                   "start": 0,
                   "end": 4},
                  {"routing_table": {0: 2, 1: None, 2: 1, 3: 0, 4: 0, 5: 4, 6: 1},
                   "start": 1,
                   "end": 6}]

        # Test on several controlled examples
        for i in range(len(INPUTS)):
            
            # Instantiate the player
            player = BFS()

            # Get the input data
            routing_table = INPUTS[i]["routing_table"]
            start = INPUTS[i]["start"]
            end = INPUTS[i]["end"]

            # Find the route
            route = player.find_route(routing_table, start, end)

            # Check the output type
            # It should be a list of integers
            self.assertTrue(isinstance(route, list))
            self.assertTrue(all(isinstance(v, int) for v in route))

            # Check that the route is a valid path from the start to the end
            self.assertEqual(route[0], start)
            self.assertEqual(route[-1], end)
            self.assertTrue(all(routing_table[route[j + 1]] == route[j] for j in range(len(route) - 1)))

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Run all tests
    unittest.main(verbosity=2)

##########################################################################################
##########################################################################################

Pour passer de DFS à BFS, il suffit de remplacer vertices_to_visit.pop() par vertices_to_visit.pop(0) dans la boucle de traversal(...). Ça revient à manipuler la liste comme une file au lieu d’une pile.

  • Créez un fichier pour lancer une partie, nommé visualize_BFS.py, dans le sous-dossier games de votre workspace PyRat.

  • Créez un fichier joueur nommé BFS.py dans le sous-dossier players. Pour ce dernier, vous pouvez partir d’une copie de votre fichier DFS.py, car il n’y aura pas beaucoup de différences !

  • Adapter les fonctions pour que votre rat effectue un parcours en largeur pour déterminer le chemin le plus court. N’oubliez pas de modifier la documentation, pour qu’elle décrive bien votre nouveau joueur.

  • N’oubliez pas non plus de tester vos fonctions ! Voici les tests que vous pouvez utiliser pour vous assurer que votre code fonctionne : tests/test_BFS.py.

    Information

    Remarquez à quel point les tests sont similaires à ceux du DFS.

    Notez également que nous avons ajouté une nouvelle fonction de test pour vérifier que nous trouvons effectivement les chemins les plus courts, sur quelques exemples contrôlés pour lesquels une seule table de routage est la solution du parcours.

Vous devriez obtenir un rat qui se comporte comme suit :

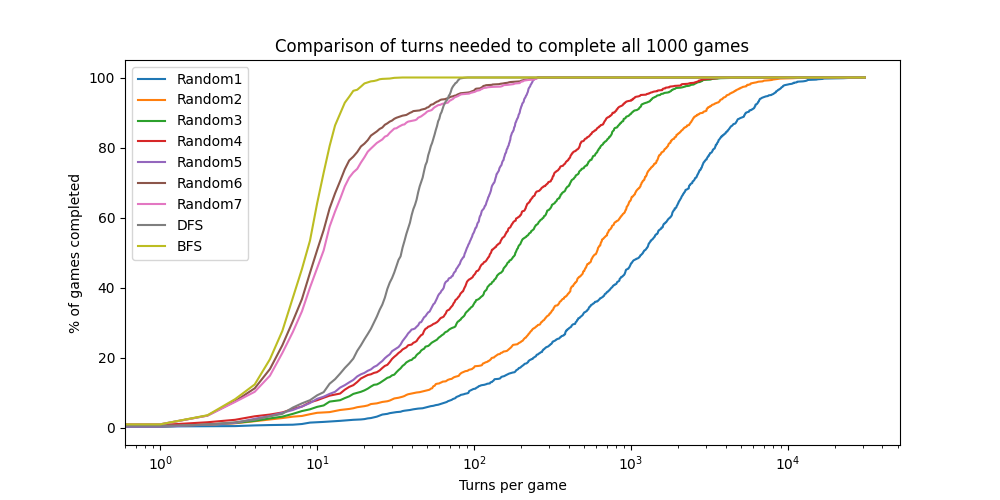
3 — Comparer aux programmes aléatoires

Maintenant que vous avez deux nouveaux joueurs, il serait intéressant de les comparer avec les joueurs aléatoires que vous avez développés lors de la séance précédente.

À faire

Adaptez (et renommez pour quelque chose de plus pertinent) le script evaluate_random_players.py pour intégrer les joueurs DFS et BFS dans l’analyse.

Essayez également de répondre aux questions suivantes :

  • Le joueur DFS prend-il un nombre moyen de tours significativement plus petit que le meilleur programme RandomX que vous avez écrit ?

  • Le joueur BFS prend-il un nombre moyen de tours significativement plus petit que DFS ?

Correction

Voici un script qui fait ça :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import tqdm.auto as tqdm
import matplotlib.pyplot as pyplot
import scipy.stats as scstats

# PyRat imports
from pyrat import Game, GameMode
from players.Random1 import Random1
from players.Random2 import Random2
from players.Random3 import Random3
from players.Random4 import Random4
from players.Random5 import Random5
from players.Random6 import Random6
from players.Random7 import Random7
from players.DFS import DFS
from players.BFS import BFS

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Determines how many games will be played for each player
    nb_games = 1000

    # Customize the game elements
    game_config = {"mud_percentage": 0.0,
                   "nb_cheese": 1,
                   "game_mode": GameMode.SIMULATION}

    # Run the games for each player class
    players = [Random1(), Random2(), Random3(), Random4(), Random5(), Random6(), Random7(), DFS(), BFS()]
    results = {player.get_name(): [] for player in players}
    for player in players:
        for seed in tqdm.tqdm(range(nb_games), desc=player.get_name()):

            # Make the game with given seed
            game = Game(random_seed=seed, **game_config)
            game.add_player(player)
            stats = game.start()

            # Store the number of turns needed
            results[player.get_name()].append(stats["turns"])

    # Visualization of cumulative curves of numbers of turns taken per program
    max_turn = max([max(results[player]) for player in results])
    pyplot.figure(figsize=(10, 5))
    for player in results:
        turns = [0] + sorted(results[player]) + [max_turn]
        games_completed_per_turn = [len([turn for turn in results[player] if turn <= t]) * 100.0 / nb_games for t in turns]
        pyplot.plot(turns, games_completed_per_turn, label=player)
    pyplot.title("Comparison of turns needed to complete all %d games" % (nb_games))
    pyplot.xlabel("Turns per game")
    pyplot.ylabel("% of games completed")
    pyplot.xscale("log")
    pyplot.legend()
    pyplot.savefig("evaluate_random_vs_traversals.png")

    # Formal statistics to check if these curves are statistically significant
    for i, player_1 in enumerate(results):
        for j, player_2 in enumerate(results):
            if j > i:
                test_result = scstats.mannwhitneyu(results[player_1], results[player_2], alternative="two-sided")
                print("Mann-Whitney U test between turns of program '%s' and of program '%s':" % (player_1, player_2), test_result)

##########################################################################################
##########################################################################################

Et voilà sa sortie :

Mann-Whitney U test between turns of program 'Random1' and of program 'Random2':
MannwhitneyuResult(statistic=np.float64(622971.5), pvalue=np.float64(1.6838248285066528e-21))

Mann-Whitney U test between turns of program 'Random1' and of program 'Random3':
MannwhitneyuResult(statistic=np.float64(785339.0), pvalue=np.float64(3.39768626337291e-108))

Mann-Whitney U test between turns of program 'Random1' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(820697.5), pvalue=np.float64(3.762123338274175e-136))

Mann-Whitney U test between turns of program 'Random1' and of program 'Random5': 
annwhitneyuResult(statistic=np.float64(905395.5), pvalue=np.float64(2.4406973722993484e-216))

Mann-Whitney U test between turns of program 'Random1' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(977330.5), pvalue=np.float64(3.3761029595058753e-299))

Mann-Whitney U test between turns of program 'Random1' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(974724.5), pvalue=np.float64(6.041532129511171e-296))

Mann-Whitney U test between turns of program 'Random1' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(957178.0), pvalue=np.float64(1.447397987042217e-274))

Mann-Whitney U test between turns of program 'Random1' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(988105.0), pvalue=np.float64(0.0))

Mann-Whitney U test between turns of program 'Random2' and of program 'Random3':
MannwhitneyuResult(statistic=np.float64(694101.0), pvalue=np.float64(4.58363795781424e-51))

Mann-Whitney U test between turns of program 'Random2' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(740510.5), pvalue=np.float64(2.0062683826941888e-77))

Mann-Whitney U test between turns of program 'Random2' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(849938.0), pvalue=np.float64(1.0005233429377223e-161))

Mann-Whitney U test between turns of program 'Random2' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(949677.5), pvalue=np.float64(8.671757626862606e-266))

Mann-Whitney U test between turns of program 'Random2' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(945624.0), pvalue=np.float64(4.868780245735369e-261))

Mann-Whitney U test between turns of program 'Random2' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(915457.5), pvalue=np.float64(4.1000721186093707e-227))

Mann-Whitney U test between turns of program 'Random2' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(965585.5), pvalue=np.float64(6.842036595918024e-285))

Mann-Whitney U test between turns of program 'Random3' and of program 'Random4':
MannwhitneyuResult(statistic=np.float64(559410.0), pvalue=np.float64(4.21035966816768e-06))

Mann-Whitney U test between turns of program 'Random3' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(691727.0), pvalue=np.float64(7.221673709238495e-50))

Mann-Whitney U test between turns of program 'Random3' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(914522.0), pvalue=np.float64(3.458538210737707e-226))

Mann-Whitney U test between turns of program 'Random3' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(905367.5), pvalue=np.float64(2.1976414998043427e-216))

Mann-Whitney U test between turns of program 'Random3' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(834328.5), pvalue=np.float64(8.339491627243258e-148))

Mann-Whitney U test between turns of program 'Random3' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(950551.0), pvalue=np.float64(5.967210168967696e-267))

Mann-Whitney U test between turns of program 'Random4' and of program 'Random5':
MannwhitneyuResult(statistic=np.float64(626983.0), pvalue=np.float64(8.061889865051033e-23))

Mann-Whitney U test between turns of program 'Random4' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(890833.0), pvalue=np.float64(2.5914219044392625e-201))

Mann-Whitney U test between turns of program 'Random4' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(879939.5), pvalue=np.float64(2.3939226363761136e-190))

Mann-Whitney U test between turns of program 'Random4' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(794050.5), pvalue=np.float64(8.654495881956927e-115))

Mann-Whitney U test between turns of program 'Random4' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(934151.5), pvalue=np.float64(4.954659276586519e-248))

Mann-Whitney U test between turns of program 'Random5' and of program 'Random6':
MannwhitneyuResult(statistic=np.float64(875418.5), pvalue=np.float64(6.51509326950569e-186))

Mann-Whitney U test between turns of program 'Random5' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(861078.0), pvalue=np.float64(4.0238170267853793e-172))

Mann-Whitney U test between turns of program 'Random5' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(761807.0), pvalue=np.float64(2.1257094003632124e-91))

Mann-Whitney U test between turns of program 'Random5' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(933008.5), pvalue=np.float64(9.449817703430092e-247))

Mann-Whitney U test between turns of program 'Random6' and of program 'Random7':
MannwhitneyuResult(statistic=np.float64(468236.5), pvalue=np.float64(0.01379698799921949))

Mann-Whitney U test between turns of program 'Random6' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(190956.0), pvalue=np.float64(1.1796295134455544e-126))

Mann-Whitney U test between turns of program 'Random6' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(597334.0), pvalue=np.float64(4.289618050994497e-14))

Mann-Whitney U test between turns of program 'Random7' and of program 'DFS':
MannwhitneyuResult(statistic=np.float64(217508.0), pvalue=np.float64(3.840436997512759e-106))

Mann-Whitney U test between turns of program 'Random7' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(632093.0), pvalue=np.float64(1.2222777727493456e-24))

Mann-Whitney U test between turns of program 'DFS' and of program 'BFS':
MannwhitneyuResult(statistic=np.float64(917496.5), pvalue=np.float64(1.4132231344750687e-229))

Du coup pour la première question :

  • Si on compare à Random5 (le meilleur de la partie obligatoire), DFS est significativement meilleur en moyenne.

  • Si on compare à Random6-7, on a bien une différence significative, et on observe que Random6-7 est meilleur en général, mais il galère sur quelques labyrinthes, alors que DFS va finir toutes ses parties en premier.

  • On pourrait utiliser la même heuristique que Random7 et trier les sommets à explorer pour DFS. Il est très probable que ça améliore les résultats.

Et pour la seconde question :

  • Oui, et on a la garantie d’avoir un chemin le plus court pour un graphe non pondéré.

Pour aller plus loin

4 — Factoriser les codes

4.1 — Similarités et différences entre DFS et BFS

Comme vous l’avez peut-être remarqué, les codes de BFS et DFS sont extrêmement similaires. En fait, c’est la structure de données utilisée qui détermine l’ordre dans lequel les sommets sont explorés. En effet, avec une file (FIFO), la traversée effectue une recherche en largeur. Avec une pile (LIFO), la traversée effectue une recherche en profondeur.

Ainsi, de manière générale, une traversée peut être vue comme un algorithme global qui, à un moment donné, doit :

  • Créer une structure de données.

  • Ajouter un élément à la structure de données.

  • Extraire un élément de la structure de données.

Le paradigme de la programmation orientée objet (POO) rend cela pratique grâce à un mécanisme appelé héritage. L’idée est de créer une classe de base qui factorise le code commun, et des sous-classes qui spécialisent les particularités.

Schématiquement, on pourrait organiser le code comme suit :

Information

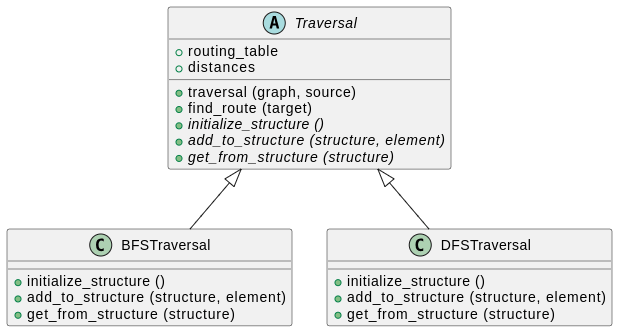
Le diagramme ci-dessus est une version simplifiée de ce que l’on appelle un diagramme de classes UML. Voici comment le lire :

  • On a trois classes : Traversal, BFSTraversal et DFSTraversal.

  • Traversal, écrit en italique, est une classe abstraite, ce qui signifie qu’on ne peut pas l’instancier. Elle sert uniquement à abstraire la notion de parcours d’un graphe et regroupe les aspects communs à toutes les algorithmes.

  • La classe Traversal possède deux attributs : routing_table et distances. Ces attributs doivent être déclarés dans le constructeur de Traversal et leur valeur définie par la méthode traversal(...).

  • La classe Traversal possède cinq méthodes : traversal(...), find_route(...), initialize_structure(...), add_to_structure(...) et get_from_structure(...). Les trois dernières sont en italique, ce qui signifie qu’elles sont abstraites, c’est-à-dire qu’elles ne font rien et doivent être implémentées dans les classes enfants.

  • Les flèches indiquent que les classes BFSTraversal et DFSTraversal héritent de Traversal. Elles ont donc accès à tous les attributs et méthodes définis dans Traversal. Contrairement à Traversal, elles sont instanciables.

  • Ces deux classes redéfinissent les méthodes abstraites de Traversal pour les rendre utilisables.

Avec cette organisation, on peut instancier bfs = BFSTraversal() et appeler la méthode bfs.traversal(...). Si traversal(...) appelle initialize_structure(...) dans son code, c’est l’implémentation de initialize_structure(...) dans BFSTraversal qui sera utilisée. À la fin, au lieu de renvoyer un résultat, traversal(...) pourra mettre à jour les attributs routing_table et distances, et on pourra accéder au résultat via bfs.routing_table et bfs.distances.

De même, on peut instancier dfs = DFSTraversal(...) et appeler dfs.traversal(...). Dans ce cas, traversal(...) utilisera l’implémentation de initialize_structure(...) dans DFSTraversal. Ainsi, le même code dans la fonction traversal(...) se comporte différemment selon la spécialisation des classes enfants.

4.2 — Implémentation

Mettons ça en pratique !

À faire

Commencez par télécharger les fichiers nécessaires, comme indiqué ci-dessous.

Correction

Suivez juste les instructions. Pas de difficultés particulières à mentionner.

  • Tout d’abord, téléchargez cette archive et extrayez son contenu dans un nouveau sous-dossier pyrat_workspace/utils. Cette archive contient un début de code pour les trois classes du diagramme ci-dessus.

  • Téléchargez ensuite ce fichier de joueur, qui contient un joueur TraversalPlayer capable d’effectuer un parcours BFS ou DFS, spécifié à la création du joueur. Placez ce fichier dans le sous-dossier players de votre workspace PyRat.

  • Enfin, téléchargez ce fichier de jeu avec BFS et ce fichier de jeu avec DFS. Placez ces fichiers dans le sous-dossier games de votre workspace PyRat.

À faire

Complétez les parties manquantes dans Traversal.py, en vous inspirant de ce que vous avez fait précédemment lors de l’activité pratique.

Correction

Le fichier final devrait ressembler à ça :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import abc

# PyRat imports
from pyrat import Graph

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class Traversal (abc.ABC):

    """
    This is an abstract class that defines the interface for graph traversal algorithms.
    It is meant to be inherited by specific traversal algorithm implementations, such as breadth-first search (BFS) or depth-first search (DFS).
    
    The class defines three abstract methods that must be implemented in the subclasses:
        * ``initialize_structure``: Initializes the data structure needed for the traversal.
        * ``add_to_structure``: Adds an element to the data structure.
        * ``get_from_structure``: Extracts an element from the data structure.
    The choice of data structure (e.g., queue, stack) will determine the behavior of the traversal algorithm.
    """

    ##################################################################################
    #                                   CONSTRUCTOR                                  #
    ##################################################################################

    def __init__ ( self,
                   *args:    object,
                   **kwargs: object
                 ) ->        None:

        """
        *(This class is abstract and meant to be subclassed, not instantiated directly).*

        Initializes a new instance of the class.

        Args:
            args:   Arguments to pass to the parent constructor.
            kwargs: Keyword arguments to pass to the parent constructor.
        """
        
        # Inherit from parent class
        super().__init__(*args, **kwargs)

        # Calling traversal will set these attributes
        self.routing_table = None
        self.distances = None

        # We store the vertex found if we stop the traversal early
        self.stop_vertex_found = None

    ##################################################################################
    #                                     METHODS                                    #
    ##################################################################################

    def traversal ( self,
                    graph:         Graph,
                    source:        int,
                    stop_vertices: set[int] | list[int] = set()
                  ) ->             None:

        """
        This method performs a traversal of the given graph from the given source vertex.
        It computes the distances from the source to all other vertices, as well as a routing table that can be used to reconstruct paths.
        The results are stored in the ``distances`` and ``routing_table`` attributes.
        
        Args:
            graph:         The graph to traverse.
            source:        The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).
            stop_vertices: A set or list of vertices at which to stop the traversal (default is an empty set, meaning the traversal will visit all reachable vertices).
        """

        # Work with sets for efficiency
        # We also allow lists as input for convenience
        stop_vertices = set(stop_vertices)

        # Initialization
        self.distances = {}
        self.routing_table = {}

        # Initialize the structure of vertices to visit
        vertices_to_visit = self.initialize_structure()
        initial_element = (0, source, None)
        vertices_to_visit = self.add_to_structure(vertices_to_visit, initial_element)

        # Traversal
        while vertices_to_visit:

            # Get the next vertex to visit
            element, vertices_to_visit = self.get_from_structure(vertices_to_visit)
            distance, vertex, parent = element

            # Skip if already visited
            # This can happen if a vertex was added multiple times to the list by different neighbors
            if vertex in self.distances:
                continue

            # Update the distances and routing table
            self.distances[vertex] = distance
            self.routing_table[vertex] = parent

            # Stop if we reached a stop vertex
            if vertex in stop_vertices:
                self.stop_vertex_found = vertex
                break

            # Add the neighbors to the list of vertices to visit
            for neighbor in graph.get_neighbors(vertex):
                distance_to_neighbor = self.distances[vertex] + graph.get_weight(vertex, neighbor)
                neighbor_element = (distance_to_neighbor, neighbor, vertex)
                vertices_to_visit = self.add_to_structure(vertices_to_visit, neighbor_element)

    ##################################################################################

    def find_route ( self,
                     target: int
                   ) ->      list[int]:

        """
        This method finds the route from the source vertex to a target vertex using a routing table.

        Args:
            target: The target vertex.

        Returns:
            The route from the source to the target as a list of vertices.
        """

        # Debug
        assert self.routing_table is not None, "Traversal must be performed before finding a route."
        assert target in self.routing_table, "Target vertex not encountered during traversal."

        # Initialization
        route = [target]
        vertex = target

        # Find the route
        while self.routing_table[vertex] != None:
            vertex = self.routing_table[vertex]
            route.append(vertex)
        
        # Reverse the route
        route.reverse()
        return route

    ##################################################################################

    @abc.abstractmethod
    def initialize_structure (self) -> object:
    
        """
        *(This method is abstract and must be implemented in the subclasses).*

        It initializes the data structure needed for the traversal.

        Returns:
            The initialized data structure.

        Raises:
            NotImplementedError: If the method is not implemented in the subclass.
        """

        # This method must be implemented in the child classes
        # By default we raise an error
        raise NotImplementedError("This method must be implemented in the child classes.")

    ##################################################################################

    @abc.abstractmethod
    def add_to_structure ( self,
                           structure: object,
                           element:   object
                         ) ->         object:
    
        """
        *(This method is abstract and must be implemented in the subclasses).*

        It adds an element to the data structure and returns the updated data structure.

        Returns:
            The updated data structure.

        Raises:
            NotImplementedError: If the method is not implemented in the subclass.
        """

        # This method must be implemented in the child classes
        # By default we raise an error
        raise NotImplementedError("This method must be implemented in the child classes.")

    ##################################################################################

    @abc.abstractmethod
    def get_from_structure ( self,
                             structure: object,
                           ) ->         tuple[object, object]:

        """
        *(This method is abstract and must be implemented in the subclasses).*

        It extracts an element from the data structure and returns it along with the updated data structure.

        Returns:
            A tuple containing the extracted element and the updated data structure.

        Raises:
            NotImplementedError: If the method is not implemented in the subclass.
        """

        # This method must be implemented in the child classes
        # By default we raise an error
        raise NotImplementedError("This method must be implemented in the child classes.")

##########################################################################################
##########################################################################################

Les fichiers BFSTraversal.py et DFSTraversal.py sont déjà fonctionnels. Regardez-les pour comprendre leurs différences.

Une fois terminé, lancez le script visualize_TraversalPlayer.py pour exécuter des parties avec le nouveau joueur.

5 — Arrêter l’algorithme de parcours plus tôt

Pour calculer les informations nécessaires pour se déplacer vers le morceau de fromage, il suffit uniquement de savoir où se trouve ce fromage. Cependant, le BFS et le DFS sont des algorithmes qui explorent le graphe jusqu’à ce que tous les sommets soient visités.

Dans notre cas, tous les calculs effectués après avoir trouvé ce morceau de fromage sont inutiles, car vous n’allez pas utiliser ces résultats. Une amélioration possible consiste donc à modifier l’algorithme de parcours pour qu’il s’arrête dès que toutes les informations nécessaires sont disponibles.

À faire

Adaptez votre algorithme de parcours (dans la version de base ou la version factorisée) pour fournir à traversal(...) une liste de sommets à trouver. L’algorithme s’arrêtera quand un de ces sommets est visité.

Est-ce plus performant en temps de calcul que de tout explorer ? Comment pourriez-vous vérifier ça ?

Correction

Le code de Traversal.py dans le fichier plus haut intègre cette fonctionnalité. En plus de s’arrêter quand un sommet de la liste est trouvé, il mémorise lequel a été trouvé dans self.stop_vertex_found.

Voilà une adaptation possible du joueur TraversalPlayer pour utiliser cette fonctionnalité :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import enum

# PyRat imports
from pyrat import Player, Maze, GameState, Action
from utils.BFSTraversal import BFSTraversal
from utils.DFSTraversal import DFSTraversal

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class TraversalAlgorithm (enum.Enum):

    """
    This enumeration defines all the possible algorithms handled by the ``TraversalPlayer``.

    Possible algorithms are:
        * ``BFS``: Breadth-first search.
        * ``DFS``: Depth-first search.
    """

    BFS = "bfs"
    DFS = "dfs"

##########################################################################################

class TraversalPlayerEarlyStop (Player):

    """
    *(This class inherits from* ``Player`` *).*

    This player controls a PyRat character that explores the maze using a graph traversal algorithm.
    The algorithm can be chosen among those defined in the ``TraversalAlgorithm`` enumeration.
    """

    ##################################################################################
    #                                   CONSTRUCTOR                                  #
    ##################################################################################

    def __init__ ( self,
                   algorithm:         TraversalAlgorithm,
                   enable_early_stop: bool = True,
                   *args:             object,
                   **kwargs:          object
                 ) ->                 None:

        """
        Initializes a new instance of the class.
        Here, the constructor is only used to initialize the player.
        It transmits the arguments to the parent constructor, which is responsible for initializing the name and the skin of the player.

        Args:
            algorithm:         The traversal algorithm to use, among those defined in the ``TraversalAlgorithm`` enumeration.
            enable_early_stop: Whether to stop the traversal as soon as a piece of cheese is found (``True``) or to traverse the whole maze (``False``).
            args:              Arguments to pass to the parent constructor.
            kwargs:            Keyword arguments to pass to the parent constructor.
        """

        # Inherit from parent class
        super().__init__(*args, **kwargs)

        # Debug
        assert isinstance(algorithm, TraversalAlgorithm), "The algorithm must be an instance of the TraversalAlgorithm enumeration"
       
        # We create an attribute to store the actions to perform
        self.actions = None

        # We initialize the chosen traversal algorithm
        self.enable_early_stop = enable_early_stop
        self.traversal_algorithm = None
        if algorithm == TraversalAlgorithm.BFS:
            self.traversal_algorithm = BFSTraversal()
        elif algorithm == TraversalAlgorithm.DFS:
            self.traversal_algorithm = DFSTraversal()

    ##################################################################################
    #                                  PYRAT METHODS                                 #
    ##################################################################################

    def preprocessing ( self,
                        maze:       Maze,
                        game_state: GameState,
                      ) ->          None:
        
        """
        *(This method redefines the method of the parent class with the same name).*

        This method is called once at the beginning of the game.
        Here, we use the traversal algorithm to compute a shortest path that reaches the piece of cheese from the initial position of the player.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        """

        # Depending on whether early stopping is enabled, we set the stop vertices to the cheese locations or to an empty set
        if self.enable_early_stop:
            early_stop_vertices = game_state.cheese
        else:
            early_stop_vertices = set()

        # We perform a traversal of the maze graph from the initial position of the player
        my_location = game_state.player_locations[self.get_name()]
        self.traversal_algorithm.traversal(maze, my_location, early_stop_vertices)
        print(f"Stop vertex found: {self.traversal_algorithm.stop_vertex_found}")

        # Find the series of locations/actions to go from the player location to the first piece of cheese
        path = self.traversal_algorithm.find_route(game_state.cheese[0])
        self.actions = maze.locations_to_actions(path)

    ##################################################################################

    def turn ( self,
               maze:       Maze,
               game_state: GameState,
             ) ->          Action:

        """
        *(This method redefines the method of the parent class with the same name).*

        It is called at each turn of the game.
        It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        
        Returns:
            One of the possible actions.
        """

        # At each turn, we perform the next action in the list of actions
        return self.actions.pop(0)

##########################################################################################
##########################################################################################

Pour aller encore plus loin

6 — Un parcours en profondeur récursif

Comme le parcours en profondeur utilise une pile, et que les fonctions récursivent exploitent la pile d’appels de fonctions pour calculer un résultat, il est assez facile de programmer un DFS récursivement.

À faire

Trouvez des ressources en ligne pour vous guidez, et lancez-vous !

Correction

Voici une implémentation possible du joueur RecursiveDFS.py :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# PyRat imports
from pyrat import Player, Maze, GameState, Action, Graph

##########################################################################################
######################################### CLASSES ########################################
##########################################################################################

class RecursiveDFS (Player):

    """
    *(This class inherits from* ``Player`` *).*

    This player performs a depth-first search (DFS) to explore the maze.
    Computation of the path is done in the ``preprocessing(...)`` method.
    The path is then followed in the ``turn(...)`` method.
    """
    
    ##################################################################################
    #                                   CONSTRUCTOR                                  #
    ##################################################################################

    def __init__ ( self,
                   *args:    object,
                   **kwargs: object
                 ) ->        None:

        """
        Initializes a new instance of the class.

        Args:
            args:   Arguments to pass to the parent constructor.
            kwargs: Keyword arguments to pass to the parent constructor.
        """

        # Inherit from parent class
        super().__init__(*args, **kwargs)

        # We create an attribute to store the actions to perform
        self.actions = None

    ##################################################################################
    #                                  PYRAT METHODS                                 #
    ##################################################################################

    def preprocessing ( self,
                        maze:       Maze,
                        game_state: GameState,
                      ) ->          None:
        
        """
        *(This method redefines the method of the parent class with the same name).*

        This method is called once at the beginning of the game.
        Here, we use a DFS algorithm to compute a path that reaches the piece of cheese from the initial position of the player.
        The actions corresponding to the path are stored in the ``actions`` attribute, and will be used in the ``turn(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        """

        # We perform a DFS traversal of the maze graph from the initial position of the player
        my_location = game_state.player_locations[self.get_name()]
        distances, routing_table = self.traversal(maze, my_location)

        # Find the series of locations/actions to go from the player location to the first piece of cheese
        path = self.find_route(routing_table, my_location, game_state.cheese[0])
        self.actions = maze.locations_to_actions(path)

    ##################################################################################

    def turn ( self,
               maze:       Maze,
               game_state: GameState,
             ) ->          Action:

        """
        *(This method redefines the method of the parent class with the same name).*

        It is called at each turn of the game.
        It returns an action to perform among the possible actions, defined in the ``Action`` enumeration.
        The action is chosen by following the path computed in the ``preprocessing(...)`` method.

        Args:
            maze:       An object representing the maze in which the player plays.
            game_state: An object representing the state of the game.
        
        Returns:
            One of the possible actions.
        """

        # At each turn, we perform the next action in the list of actions
        return self.actions.pop(0)

    ##################################################################################
    #                                  OTHER METHODS                                 #
    ##################################################################################

    def traversal ( self,
                    graph:  Graph,
                    source: int
                  ) ->      tuple[dict[int, int], dict[int, int | None]]:

        """
        This method performs a recursive DFS traversal of a graph.
        It returns the explored vertices with associated distances.
        It also returns the routing table, that is, the parent of each vertex in the traversal.
        
        Args:
            graph:  The graph to traverse.
            source: The source vertex of the traversal (we type it as int here because we will only manipulate mazes, but Graph uses Hashable as a more generic type).

        Returns:
            A tuple containing:
            - The distances from the source to each explored vertex.
            - The routing table, that is, the parent of each vertex in the traversal (None for the source).
        """

        # Initialization
        distances = {}
        routing_table = {}

        # Recursive subfunction that performs the DFS traversal
        def __dfs ( visited_vertices: set[int],
                    current_vertex:   int,
                    current_distance: int,
                    parent_vertex:    int | None
                  ) ->                None:

            # Mark the current vertex as visited
            visited_vertices.add(current_vertex)

            # Store the distance and parent of the current vertex
            nonlocal distances, routing_table
            distances[current_vertex] = current_distance
            routing_table[current_vertex] = parent_vertex

            # Explore the neighbors of the current vertex
            for neighbor in graph.get_neighbors(current_vertex):
                if neighbor not in visited_vertices:
                    __dfs(visited_vertices, neighbor, current_distance + 1, current_vertex)
        
        # Use the recursive subfunction to perform the DFS traversal from the source
        __dfs(set(), source, 0, None)
        return distances, routing_table

    ##################################################################################

    def find_route ( self,
                     routing_table: dict[int, int | None],
                     source:        int,
                     target:        int
                   ) ->             list[int]:

        """
        This method finds the route from a source vertex to a target vertex using a routing table.

        Args:
            routing_table: The routing table, that is, the parent of each vertex in the traversal (None for the source).
            source:        The source vertex.
            target:        The target vertex.

        Returns:
            The route from the source to the target as a list of vertices.
        """

        # Initialization
        route = [target]
        vertex = target

        # Find the route
        while vertex != source:
            vertex = routing_table[vertex]
            route.append(vertex)
        
        # Reverse the route
        route.reverse()
        return route

##########################################################################################
##########################################################################################

Et un script de jeu pour visualiser ce joueur :

​
##########################################################################################
########################################## INFO ##########################################
##########################################################################################

"""
This program is a solution to the practical session 2 of the PyRat project:
https://hub.imt-atlantique.fr/ueinfo-fise1a/s5/project/session2/practical/
"""

##########################################################################################
######################################### IMPORTS ########################################
##########################################################################################

# External imports
import pprint

# PyRat imports
from pyrat import Game
from players.RecursiveDFS import RecursiveDFS

##########################################################################################
######################################### SCRIPT #########################################
##########################################################################################

if __name__ == "__main__":

    # Instantiate a game with a few arguments
    game_config = {"mud_percentage": 0.0,
                   "maze_width": 13,
                   "maze_height": 10,
                   "nb_cheese": 1,
                   "random_seed": 42,
                   "trace_length": 1000}

    # Instantiate a game with specified arguments
    game = Game(**game_config)

    # Instantiate the player
    player = RecursiveDFS()
    game.add_player(player)

    # Start the game
    stats = game.start()
    pprint.pprint(stats)

##########################################################################################
##########################################################################################

7 — Programmation défensive

Dans les fichiers de tests que nous vous avons fournis, nous n’avons testé que le comportement attendu de la méthode testée. Lorsqu’on programme en pensant à un utilisateur, il est également recommandé d’anticiper les erreurs que l’utilisateur pourrait commettre et de lever une exception dans ce cas. Ceci s’appelle la programmation défensive.

Dans le cas de test_DFS.py, on pourrait par exemple imaginer les erreurs suivantes :

  • Appeler la fonction traversal(...) à partir d’un sommet de départ qui n’existe pas.
  • Appeler la fonction traversal(...) sur un labyrinthe qui n’est pas connexe (c’est à dire qu’il existe des cases telles qu’aucun chemin ne permet d’aller de l’une à l’autre).
  • Appeler la fonction traversal(...) avec des arguments inattendus.
  • Appeler la fonction find_route(...) avec un sommet de départ qui n’existe pas.
  • Appeler la fonction find_route(...) avec un sommet d’arrivée qui n’existe pas.
  • Appeler la fonction find_route(...) avec des arguments inattendus.
  • Appeler la fonction find_route(...) avec une table de routage invalide.
  • Appeler la fonction find_route(...) avec des sommets de départ et d’arrivée qui ne peuvent pas être reliés par un chemin.

Dans ces cas, il aurait été utile pour l’utilisateur d’obtenir une exception personnalisée, indiquant son erreur. Pour ce qui est des tests unitaires, vous pouvez vérifier que ces exceptions sont bien levées en utilisant self.assertRaises(...).

À faire

Complétez vos méthodes pour ajouter des assert ... permettant de lever une exception quand un comportement inattendu est détecté. Puis, étendez vos fichiers de tests pour vérifier que ces exceptions sont bien levées dans les cas identifiés.

Pour un exemple, vous pouvez consulter le fichier Traversal.py fourni dans l’archive plus haut. Si l’on appelle find_route(...) avant d’avoir appelé traversal(...), une exception sera levée, car la table de routage n’a pas encore été initialisée.

8 — L’algorithme IDDFS

Une autre piste que vous pouvez explorer est de programmer un algorithme appelé IDDFS. Cet algorithme combine des aspects des algorithmes BFS et DFS, tout en nécessitant moins de mémoire que les deux.

À faire

Implémentez cet algorithme (ou trouvez une bibliothèque qui le propose).

9 — L’algorithme de Seidel

Alors que le BFS fournit le plus court chemin d’un sommet vers tous les autres, l’algorithme de Seidel permet d’obtenir les plus courts chemins entre tous les sommets dans un graphe non pondéré.

À faire

Implémentez cet algorithme (ou trouvez une bibliothèque qui le propose).