Tas min

En bref

Résumé de l’article

Dans cet article, vous apprendrez ce qu’est un tas min (min-heap), une structure de données avec des propriétés particulières. Elle sera très utile pour implémenter l’algorithme de Dijkstra.

À retenir

• Les tas min sont des structures de données où les données sont extraites en fonction d’une valeur de référence.

• Ils peuvent être utilisés pour implémenter facilement l’algorithme de Dijkstra.

• Il existe plusieurs façons de programmer un tas min, certaines étant plus efficaces que d’autres.

• En Python, la bibliothèque heapq fournit une bonne implémentation des tas min.

Contenu de l’article

1 — Vidéo

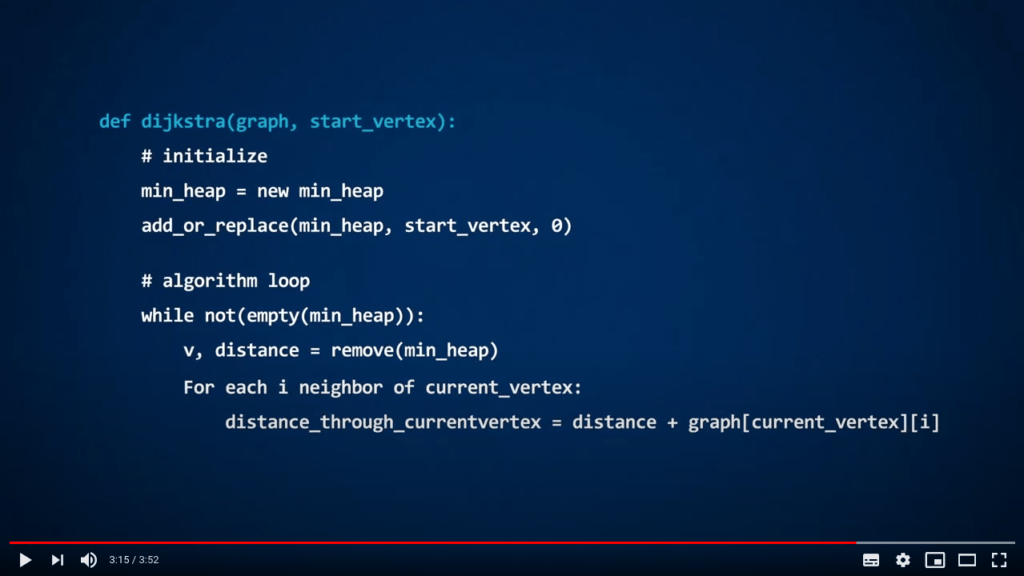
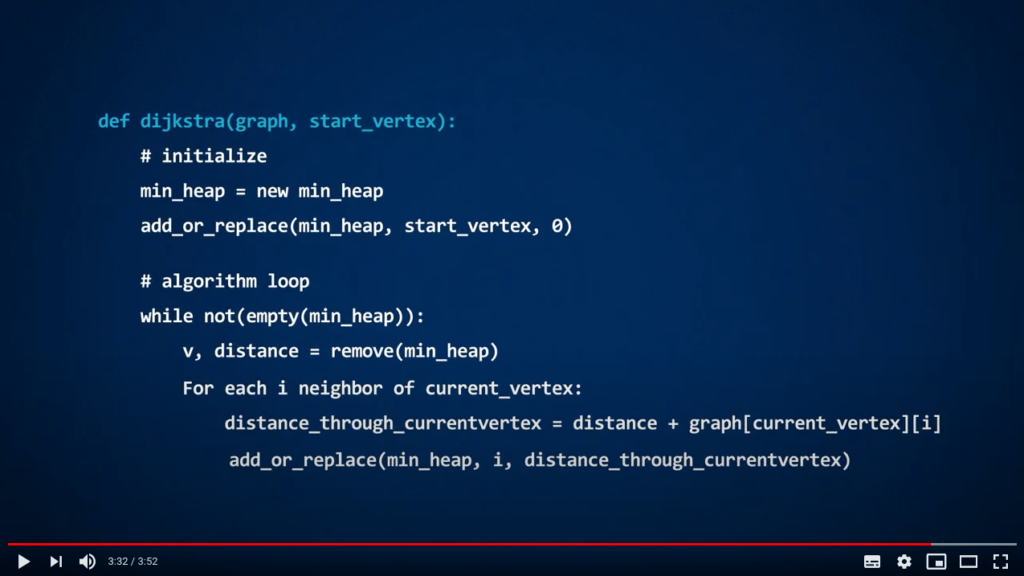
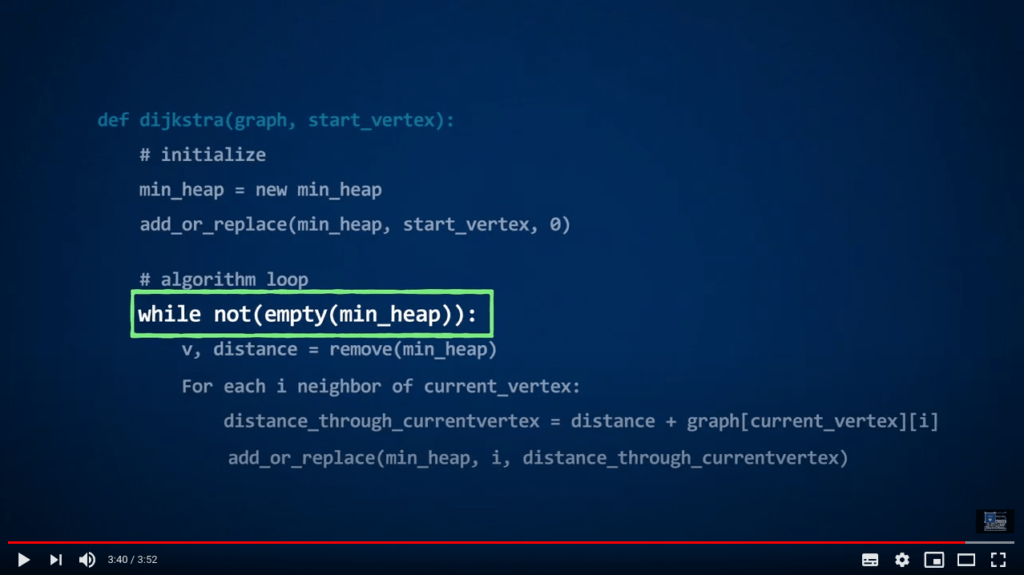
Veuillez consulter la vidéo ci-dessous (en anglais, affichez les sous-titres si besoin). Nous fournissons également une traduction du contenu de la vidéo juste après, si vous préférez.

Voici quelques remarques importantes sur cette vidéo :

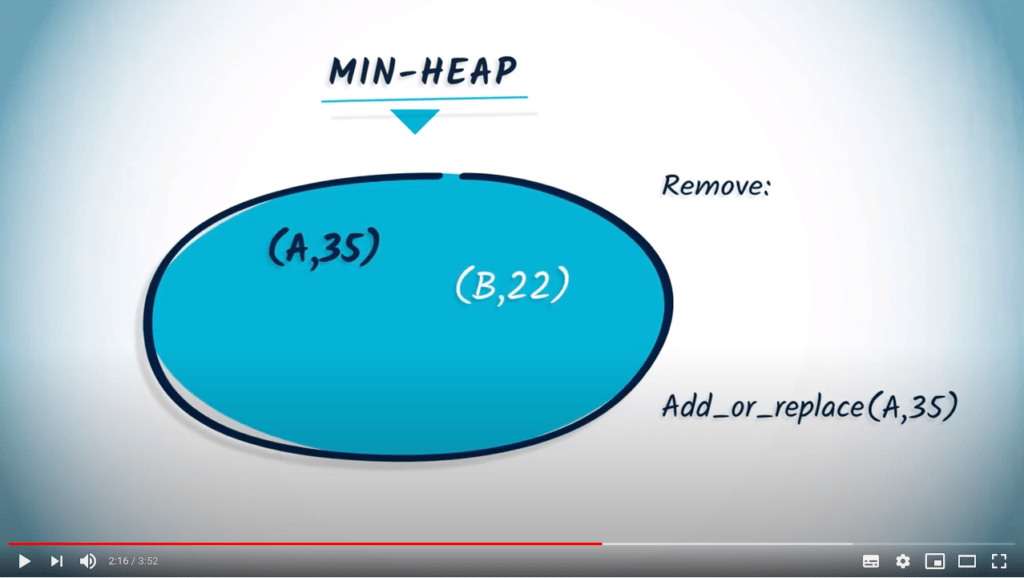
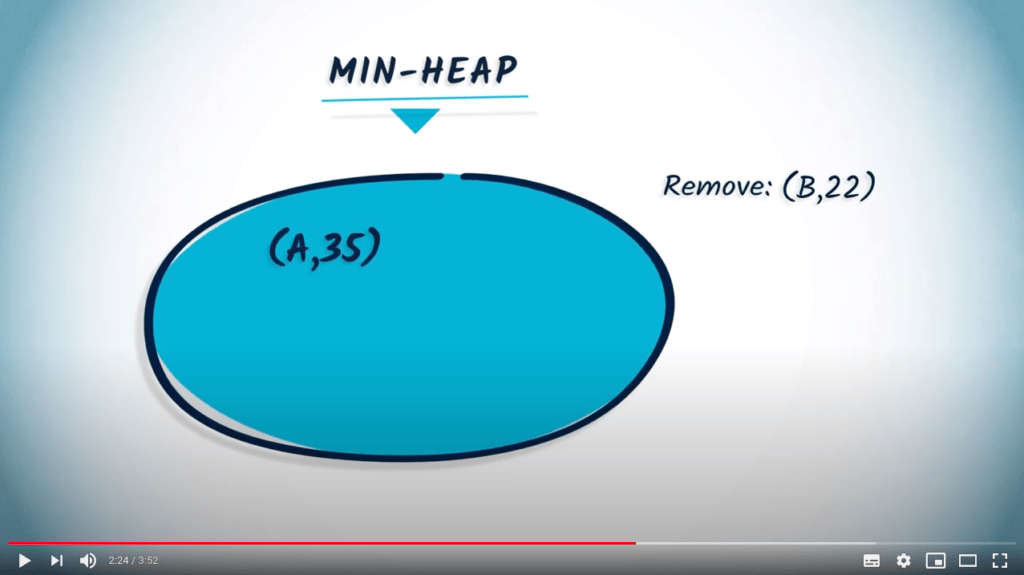
• Dans cette vidéo, nous avons utilisé les termes “clé” (l’élément que nous voulons stocker) et “valeur” (son importance dans le tas). D’autres terminologies existent ! L’aspect important est que remove(...) doit retourner l’élément minimum de la structure. Attention à la manière dont ce minimum est calculé !

• Dans la vidéo, une implémentation possible de l’algorithme de Dijkstra est présentée, utilisant une fonction appelée add_or_replace(...). Ici, nous expliquons simplement ce que fait cette fonction, mais nous ne fournissons pas son code. Lorsque vous implémenterez l’algorithme en Python, vous devrez créer une telle fonction ou réfléchir à une autre solution.

Pour aller plus loin

2 — Une implémentation naïve d’un tas min utilisant une liste

Une manière simple (mais assez inefficace) d’implémenter un tas min est d’utiliser une liste pour stocker des paires (clé, valeur). Dans cette section, nous montrons comment créer un tas min comme ça.

Créons une classe pour notre tas min naïf. Cela permettra de créer un nouveau tas min et d’effectuer des opérations dessus :

class ListBasedMinHeap ():

    """
    A simple implementation of a min-heap using a list.
    This implementation is not efficient, but it is easy to understand.
    """

Dans le constructeur de notre classe, nous créons un attribut pour stocker les éléments. Dans cette implémentation, nous créons simplement une liste vide :

def __init__ (self) -> None:

    """
    Constructor of the class.
    We create an empty list to store the elements of the min-heap.
    """

    # We create an attribute to store the elements
    self.elements = []

Maintenant, nous devons définir les deux méthodes présentées dans la vidéo : add_or_replace(...) et remove(...). Commençons par la première.

Nous allons procéder comme suit :

• Tout d’abord, nous vérifions si la liste contient la clé que nous voulons ajouter.
• Si c’est le cas, et que la valeur associée est supérieure à la valeur que nous voulons ajouter, nous la supprimons.
• Enfin, nous ajoutons la paire (clé, valeur) que nous voulons stocker si nécessaire.

Cela correspond au code suivant :

def add_or_replace ( self,
                     key:   object,
                     value: float
                   ) ->     None:

    """
    Add a (key, value) pair to the min-heap.
    If the key already exists, and its associated value is greater than the value to add, then the value is updated with the new value.
    If the value is smaller, then the operation is ignored.

    Args:
        key:   The key to add.
        value: The value associated with the key.
    """

    # We check if the key is already in the heap
    index = None
    for i in range(len(self.elements)):
        if self.elements[i][0] == key:
            index = i
            break

    # If the key is already in the heap, we remove the previous element if the new value is lower
    add_new_element = True
    if index is not None:
        if value < self.elements[index][1]:
            del self.elements[index]
        else:
            add_new_element = False

    # We add the new element
    if add_new_element:
        self.elements.append((key, value))

En termes de complexité, cette implémentation doit parcourir toute la liste des éléments. Comme cette liste peut contenir jusqu’à $n$ éléments, où $n$ est le nombre de sommets dans le graphe, elle est de complexité $O(n)$.

Maintenant, pour retirer un élément, comparons simplement les valeurs de tous les éléments dans la liste, et retournons celui avec la plus petite valeur :

def remove (self) -> tuple[object, float]:

    """
    Remove and return the (key, value) pair with the smallest value from the min-heap.

    Returns:
        A tuple (key, value) corresponding to the element with the smallest value.
    """

    # We find the element with the smallest value
    min_index = 0
    for i in range(1, len(self.elements)):
        if self.elements[i][1] < self.elements[min_index][1]:
            min_index = i

    # We remove the element with the smallest value
    key, value = self.elements[min_index]
    del self.elements[min_index]

    # We return the key and value of the element removed
    return key, value

En termes de complexité, cette implémentation est de complexité $O(n)$ pour les mêmes raisons que celles mentionnées ci-dessus.

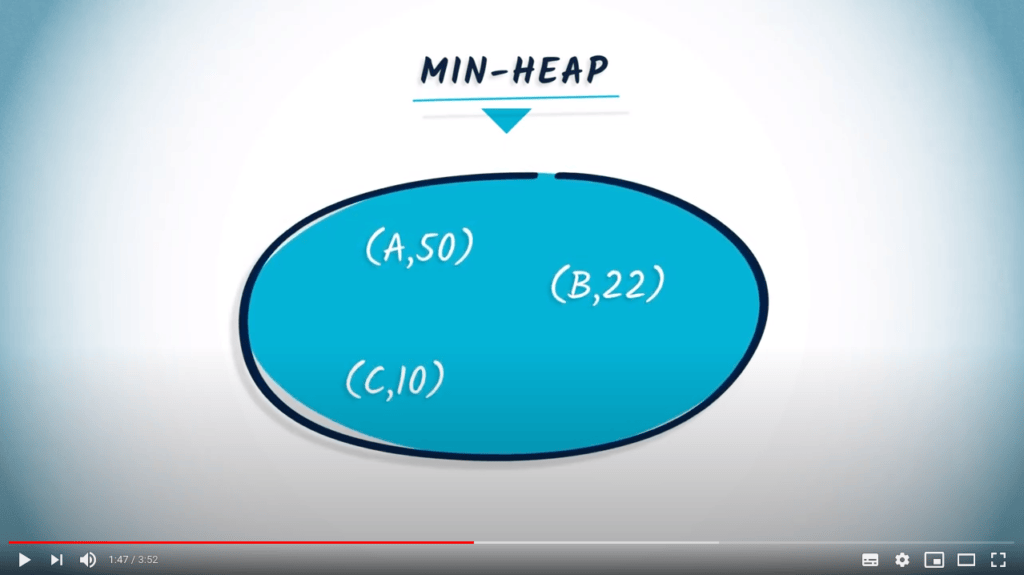
Testons notre tas min en utilisant le même exemple que dans la vidéo :

# Create a min-heap
heap = ListBasedMinHeap()

# Add elements to the heap
heap.add_or_replace("A", 50)
heap.add_or_replace("B", 22)
heap.add_or_replace("C", 10)

# Show the elements of the heap
print("Heap initial state:", heap.elements)

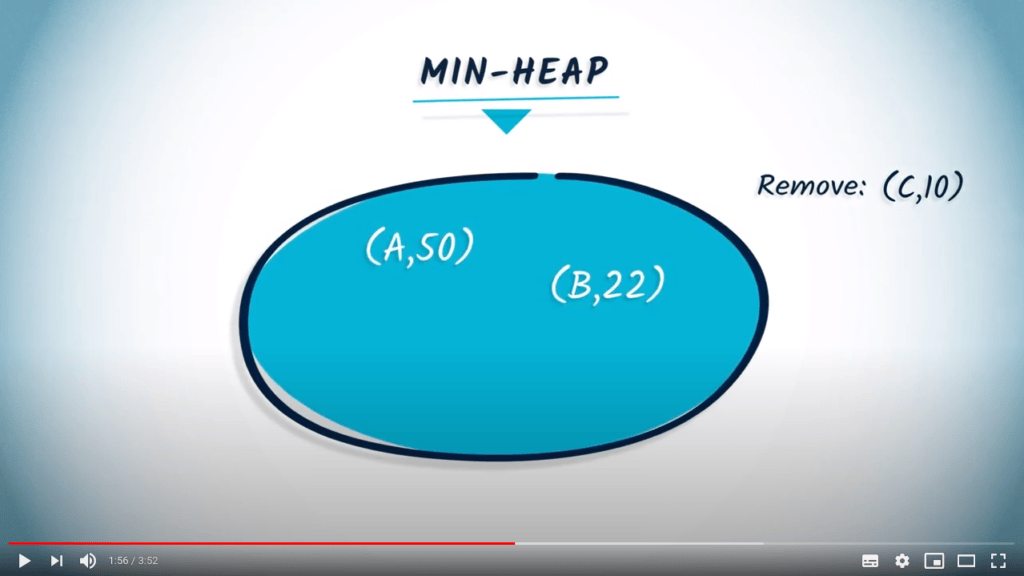
# Remove the element with the smallest value
key, value = heap.remove()
print("Removed:", key, value)
print("Heap after remove():", heap.elements)

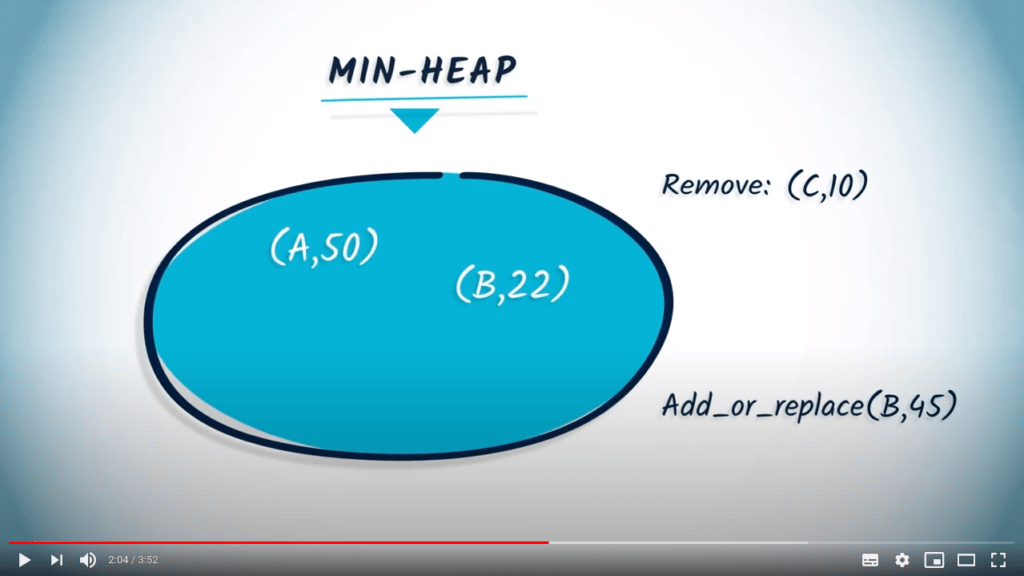
# Add a new element to the heap
heap.add_or_replace("B", 45)
print("Heap after add_or_replace(B, 45):", heap.elements)

# Add a new element to the heap
heap.add_or_replace("A", 35)
print("Heap after add_or_replace(A, 35):", heap.elements)

# Remove the element with the smallest value
key, value = heap.remove()
print("Removed:", key, value)
print("Heap after remove():", heap.elements)

Voici la sortie que nous obtenons :

Heap initial state: [('A', 50), ('B', 22), ('C', 10)]
Removed: C 10
Heap after remove(): [('A', 50), ('B', 22)]
Heap after add_or_replace(B, 45): [('A', 50), ('B', 22)]
Heap after add_or_replace(A, 35): [('B', 22), ('A', 35)]
Removed: B 22
Heap after remove(): [('A', 35)]

Vous voulez essayer par vous-même ? Voici une implémentation de cette classe. Si vous souhaitez l’utiliser dans vos programmes, n’hésitez pas à la copier dans un répertoire pyrat_workspace/utils.

3 — Une meilleure implémentation

Eh bien, $n$ opérations pour ajouter un élément, et $n$ opérations pour en retirer un, ce n’est pas très efficace. Ainsi, la complexité de l’implémentation naïve de add_or_replace(...) a un impact sur les performances du code et la consommation d’énergie.

Il est assez évident que nous pouvons faire mieux, par exemple en gardant la liste triée, de sorte que remove(...) ait simplement à retourner le premier élément. Avec une telle adaptation, remove(...) aurait une complexité de $O(1)$, au prix d’un surcoût computationnel dans add_or_replace(...).

En pratique, il existe des solutions encore meilleures, basées sur des structures de données plus complexes. En Python, nous pouvons utiliser une bibliothèque appelée heapq. Cette bibliothèque fournit deux méthodes :

• heappush(...), qui ajoute un élément au tas min.
• heappop(...), qui retire l’élément minimum du tas min.

Voyons ce qui se passe avec le même exemple que dans la vidéo :

# Import heapq
import heapq

# Create a min-heap
heap = []

# Add elements to the heap
heapq.heappush(heap, ("A", 50))
heapq.heappush(heap, ("B", 22))
heapq.heappush(heap, ("C", 10))

# Show the elements of the heap
print("Heap initial state:", heap)

# Remove the element with the smallest value
key, value = heapq.heappop(heap)
print("Removed:", key, value)
print("Heap after heappop():", heap)

# Add a new element to the heap
heapq.heappush(heap, ("B", 45))
print("Heap after heappush(B, 45):", heap)

# Add a new element to the heap
heapq.heappush(heap, ("A", 35))
print("Heap after heappush(A, 35):", heap)

# Remove the element with the smallest value
key, value = heapq.heappop(heap)
print("Removed:", key, value)
print("Heap after heappop():", heap)

Semble assez similaire à ce que nous avions avant, n’est-ce pas ? Eh bien, voyons la sortie :

Heap initial state: [('A', 50), ('B', 22), ('C', 10)]
Removed: A 50
Heap after heappop(): [('B', 22), ('C', 10)]
Heap after heappush(B, 45): [('B', 22), ('C', 10), ('B', 45)]
Heap after heappush(A, 35): [('A', 35), ('B', 22), ('B', 45), ('C', 10)]
Removed: A 35
Heap after heappop(): [('B', 22), ('C', 10), ('B', 45)]

Ce que fait cette bibliothèque, c’est qu’elle retourne l’élément minimum parmi ceux qui ont été ajoutés. Ici, les éléments sont des paires, donc heapq déterminera quelle paire est la plus petite en vérifiant leur contenu dans l’ordre lexicographique, i.e., le premier élément de la paire, puis le second. Dans l’exemple ci-dessus, les comparaisons sont faites sur "A", "B" et "C" plutôt que sur les valeurs numériques, qui ne sont utilisées qu’en cas d’égalité sur la première entrée.

Corrigeons cela en inversant les clés et les valeurs :

# Import heapq
import heapq

# Create a min-heap
heap = []

# Add elements to the heap
heapq.heappush(heap, (50, "A"))
heapq.heappush(heap, (22, "B"))
heapq.heappush(heap, (10, "C"))

# Show the elements of the heap
print("Heap initial state:", heap)

# Remove the element with the smallest value
value, key = heapq.heappop(heap)
print("Removed:", key, value)
print("Heap after heappop():", heap)

# Add a new element to the heap
heapq.heappush(heap, (45, "B"))
print("Heap after heappush(45, B):", heap)

# Add a new element to the heap
heapq.heappush(heap, (35, "A"))
print("Heap after heappush(35, A):", heap)

# Remove the element with the smallest value
value, key = heapq.heappop(heap)
print("Removed:", key, value)
print("Heap after heappop():", heap)

Voici la sortie que nous obtenons maintenant :

Heap initial state: [(10, 'C'), (50, 'A'), (22, 'B')]
Removed: C 10
Heap after heappop(): [(22, 'B'), (50, 'A')]
Heap after heappush(45, B): [(22, 'B'), (50, 'A'), (45, 'B')]
Heap after heappush(35, A): [(22, 'B'), (35, 'A'), (45, 'B'), (50, 'A')]
Removed: B 22
Heap after heappop(): [(35, 'A'), (50, 'A'), (45, 'B')]

Mieux déjà, mais il semble que heappop(...) ne réalise pas d’opération de remplacement lorsque la clé existe déjà. En effet, il se contente d’ajouter des éléments à une structure, sans réelle notion de “clés” ou de “valeurs”. Il a simplement la propriété de retourner l’élément minimum lorsqu’on le demande.

Alors, comment peut-on utiliser cela pour implémenter l’algorithme de Dijkstra ? En fait, il est possible d’adapter simplement l’algorithme vu dans le cours. En effet, lorsqu’un sommet est extrait du tas min, vous savez que vous avez trouvé le chemin le plus court vers ce sommet. Ainsi, si vous extrayez plus tard le même sommet, vous savez qu’il s’agit d’un chemin plus long, et vous pouvez donc simplement l’ignorer !

Eh bien, cela ne nous dit pas si cette solution est meilleure que la solution naïve. En réalité, heapq est un tas binaire, et les opérations heappush(...) et heappop(...) ont une complexité de $O(log_2(n))$, ce qui est inférieur à $O(n)$. Nous donnons plus de détails ci-dessous si vous le souhaitez.

4 — Implémentation utilisant un arbre binaire équilibré

4.1 — Définitions

Commençons par quelques définitions. Vous devriez déjà savoir ce qu’est un arbre, et ce que nous appelons sa racine. Un sommet dans un arbre est un “nœud” s’il a des voisins plus éloignés de la racine de l’arbre (que nous appelons enfants). Sinon, c’est une “feuille”.

La “profondeur” d’un arbre est la longueur du plus long chemin le plus court partant de la racine. Un arbre est “équilibré” si tous ses chemins les plus courts partant de la racine ont la même longueur, $\pm 1$.

4.2 — Le modèle d’arbre

Au lieu d’utiliser une liste, il est proposé d’utiliser un arbre binaire équilibré avec les propriétés suivantes :

• Chaque nœud de l’arbre est associé à un couple (clé, valeur). Cette propriété permet de lier l’arbre aux éléments à stocker/extraire.

• Chaque nœud parent a deux enfants, sauf si le nombre total d’éléments dans la structure est impair, auquel cas un seul nœud a un seul enfant et tous les autres en ont deux.

• L’arbre est équilibré. Cette propriété garantit que l’arbre ne prend pas une forme similaire à une longue chaîne, en devenant une sorte de liste, perdant ainsi tout l’intérêt d’utiliser des arbres.

• La valeur d’un parent est toujours inférieure à celle de ses enfants. Cette propriété essentielle garantit que le nœud de valeur minimale est toujours à la racine.

4.3 — Création

Pour initialiser une telle structure de priorité, il suffit de retourner un arbre vide.

4.4 — Insertion

Pour insérer un couple (clé, valeur) dans l’arbre, procédez comme suit :

1. Le couple (clé, valeur) est ajouté à la fin de l’arbre, i.e. :

• Si tous les nœuds parents ont deux enfants, une feuille de profondeur minimale est transformée en parent de ce nœud.
• Si un nœud parent n’a qu’un seul enfant, il est ajouté comme second enfant de ce nœud.

2. Si la valeur de ce nouveau nœud est inférieure à celle de son parent, les couples (clé, valeur) du nœud et de son parent sont échangés.

3. On continue en remontant dans l’arbre autant que nécessaire.

Puisque nous ne faisons que remplacer des éléments dans l’arbre par des éléments de valeurs plus petites, l’arbre résultant conserve les propriétés énoncées si l’arbre d’origine les avait.

4.5 — Extraction

Pour extraire un élément, procédez comme suit :

1. Le couple (clé, valeur) associé à la racine de l’arbre est retourné.

2. On le remplace par une feuille de profondeur maximale de l’arbre.

3. Si la nouvelle racine a une valeur supérieure à l’une de ses enfants, le couple (clé, valeur) est échangé avec l’enfant de plus petite valeur.

4. On recommence en descendant autant que nécessaire.

Ici encore, il est facile de vérifier que l’arbre résultant respecte les propriétés énoncées si l’arbre de départ les respectait également.

4.6 — Complexité

La complexité des opérations d’insertion et d’extraction nécessite d’aller de la racine à une feuille de profondeur maximale dans le pire des cas. L’arbre étant binaire, cela représente $log_2(n)$ opérations, où $n$ est le nombre d’éléments dans la structure. Nous sommes donc beaucoup moins complexes qu’avec une implémentation naïve utilisant une liste (où le nombre d’opérations était au moins linéaire en $n$).

Pour aller plus loin

• Priority queue.

  Une liste plus complète des structures de données de priorité.

• Implementation of A*.

  L’algorithme de parcours A* est quelque chose que vous pourriez vouloir essayer dans le projet.